A Routing Priority Scheduling Algorithm for MAC Layer in Wireless Sensor Networks

Published Online April 2011 in MECS

With the rapid development of chips, communication and sensing technologies, sensing technology are entering a new era of wireless sensor networks [1]. The tiny sensing nodes, which consist of sensing, data processing and wireless communication components in WSNs, are deployed densely and randomly in large numbers [2]. The tiny nodes form the network in a self-organization manner. Based on the diverse onboard sensors, the WSNs can sense the field and communicate information to the remote sink in an efficient and timely manner. The sensing performance and reliability have been improved significantly in WSNs. So the WSNs can be widely used in military sensing, security, environmental monitoring, traffic surveillance, medical treatment, building and structures monitoring, even anti-terrorism, etc.

However, since the sensor nodes are battery driven and it is impractical to recharge the battery for so many nodes after deployment, energy efficiency has been a key concern in the research work of WSNs [3-7]. In many WSNs applications, the data gathering has the Quality of Services (QoS) requirements in terms of BER performance, end-to-end timeliness and reliability, etc. Therefore, to design the scheme with low energy consumption and flexible QoS provisioning is the guarantee for the efficient information gathering in WSNs [8]. According to the analysis of sensor nodes, the main sources of energy consumption are sensing, wireless transmission and data processing. And the energy consumption caused by wireless transmission is much more than sensing and data processing. On the other hand, since most technologies in WSNs, such as data routing, distributed information processing which has the requirements for wireless transmission. Wireless transmission technologies have been identified as the key technologies determining the energy consumption and QoS, which are also the basis for other technologies [9]. Generally, distance between Cluster head and other cluster head is farther, as illustrated in the Fig.1. Wireless transmission between the different clusters also need more power of radio. Therefore, the high-efficient communication between the different clusters appropriate for low energy consumption system remains the key and hot issue in WSNs researches.

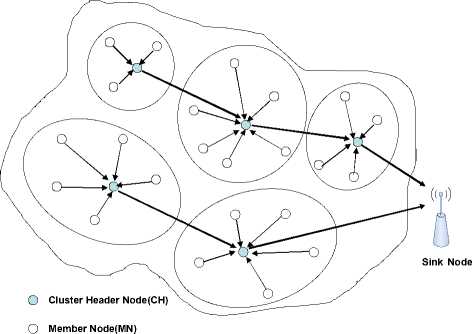
’      * Communication between the different clusters

------► Communication within the cluster

Figure 1. WSNs network topology structure model

As we all know, the quality of WSNs service mechanism determines the quality of network service [10]. Quality of Service (QoS) is always basic and hot issue in WSNs [11]. However, the current research mainly focuses on the routing algorithms in a network layer, while the end-to-end performance guarantees can not be only provided by routing or QoS routing, it is needed to investigate the other layers which allocates resources. Medium Access Control (MAC) protocol is an important part in the network protocol stack of WSNs, and it is mainly used to coordinate nodes to access the shared wireless channel. Like the situation in which contention conflicts occur when multiple accesses is introduced in the computer network, several nodes may contend for a single or server channels in communication when several nodes simultaneously request accesses in shared media. MAC protocol can utilize the limited wireless resource and plays a crucial role in WSNs performance at this stage. So the research of MAC protocol and related techniques in WSNs is significant.

Hierarchical management is widely applied in the wireless sensor networks. It can not only provide flexible, reliable communication, but also promotes the expansibility of the network [12-13]. The network is divided into clusters, which are composed of the cluster head node and some member nodes. These cluster head nodes can further form the higher-level cluster according to the requirement of the application. The cluster head node is responsible for the coordination, the data transfer and the management of all the nodes in the cluster. Moreover, the cluster head can be pre-assigned or elected automatically. Corresponding to these characteristics this dissertation proposes an algorithm for polling scheme based on clustering. Usually clustering is an important method for hierarchy control in WSNs and maps the dynamic topology onto a relatively fixed architecture with multi-hop to single-hop communication in a cluster. In the suggested algorithm Cluster Header (CH) polls the active nodes in a polling table which is used to register node addresses and priorities in a cluster to guarantee a QoS scheme of differentiated traffic priorities. The polling scheme not only avoids collisions but also reduces energy consumption for the only services to active nodes [4]. Furthermore, priority-based services can save energy to a large extent. Therefore, in this thesis, the author carried out deep and systematic research work on the energy efficiency and QoS guaranteeing by establishing Cluster-based MAC Scheme in WSNs.

Polling for the resource allocation in the system service provides a periodic access control mechanisms that can effectively prevent access to the site of competition between the conflicts, especially in high-load conditions can be obtained on better utilization of shared resources [14, 15]. In recent decades, scholars at home and abroad theoretical research polling system to achieve fruitful results. Researchers have roundly analyzed three kinds of basic services strategy of polling system such as gated, exhaustive and limited services [14-19]. The research polling system is also widely used in industry control, communication networks, production management and economic development, forecasting and other fields.

With the increased requirements for network service and multimedia performance, it is urgent to break away from the single polling policy strategy and to develop new control strategies for different inquiry service order and mixed service on the basis of cyclic access. In this sense, polling control theories demand further development [20-22]. In the MAC control protocol of a communications network, application of the prioritybased polling mechanism under mixed service policy will further optimize the system service, with striking pertinence and flexibility. Currently, the research concentration in polling is the establishment of real-time, robust and high-quality QoS for multi-priority services.

Based on queuing theory [16, 17], this research established the two-class priority node gated polling system. The system is made up of one Cluster Head (CH), one key node h , and N common nodes. The higher-priority key node applies an exhaustive-service policy with less time delay, which fits for the communication between the cluster and its upstream cluster head node. Meanwhile, the lower-priority common nodes use the gated policy to facilitate data transmissions within the cluster . The higher and the lower nodes receive alternatively the polling connection service from CH. System model is shown in Fig.2.

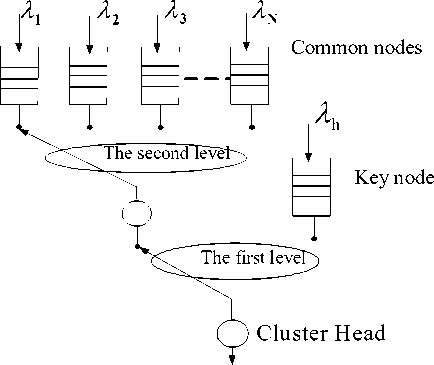
Figure 2. System Model

Markov chain and multi-dimensional probability generating function are applied to produce the systematic mathematical model, from which probability generating function of the system status variable is derived. Mathematical analysis and simulated experiments are made on the mean queue length and the mean cyclic time of the key node and the common nodes.

• II.    T HE T HEORETICAL M ODEL OF THE S CHEME

• A.    The Operational Mechanism and Variable Definition of the System Model

Polling services at each node include the following processes:

When the arrival process meets with the condition of Poisson , the information packets entering each common node follow the independent and identical distribution of probability, with mean value respectively as Ai( i = 1,2,L, N) X . The information packets entering key node follow the same independent and identical distribution of probability, with mean value respectively as pXh ,0 < p < 1 .The CH polls at the i (i = 1,2, L , N) common node at the time of tn, with the information packets waiting to be transmitted in the i node is Ei(n) , and the system status variable being {E1(n), E2(n)L , EN (n), Eh (n)} . The CH provides transmission service for the i common node under the limited (k = 1) service policy. After its service for the i node, the server starts to poll at the key node via a transfer time of ui (n) , with the information packets entering the j node (j = 1,2,L , N, h) at the time of ui ( n ) is ц j ( ui) . Then, the CH inquires the information packets queuing for transmission in the memory of the key node at the time of t* . At this moment, the number of n information packets queuing for transmission in the memory of the key node is Eh (n ) and the system status variable is {E1(n*), E2(n*)L , EN (n*), Eh (n*)} • If the memory of the key node is not blank, the transmission of information packets is completed via exhaustive service rules. When the memory of the central station is blank, the CH starts the transmission service for the information packets in the i +1 common node at the time of tn+1. At this moment, the system status variable is E (n +1), £ (n + 1)L, En (n +1), Eh (n +1)}.

• B.    The Operational Conditions for the System According to the operational process of the system, the operational conditions are defined as follows:

• 1)    The time of information packets transmission in the memory the common node follows an independent and identically distributed probability, with its LST is B % ( s ) , and the second-order origin moment respectively is - B '( 0 ) = p and J%'( 0 ) = % ( 0 ) ;

• 2)    The time of information packets transmission in the memory the key node follows an independent and identically distributed probability, with its LST is B f ( s ) , and the mean and the second-order origin moment respectively is - B ‘ ( 0 ) = Д and B % ( 0 ) ;

• 3)    The transfer time when the CH polls from the i node to the key node follows an independent and identically distributed probability, with its LST being % ( s ), and the second-order origin moment respectively is — R % ( 0 ) = / and % 0 ) = R ( 0 ) .

• 4)    The static variable of the time for the exhaustive service of information grouping arriving at the key node follows an independent and identical distribution of probability, with the distributional probability generating function as H_h (0) ;

• 5)    The CH serves the information packets in the memory of each station based on the FCFS rule. There is enough capacity of the memory at each terminal station so that information packets will not overflow or get lost.

• C.    Probab l ty Generat ng Funct on of the System Status Var able

When the CH serves the i +1 station at the time of t n _{+ 1}, the equation goes as:

Г ,( ( n +1) = 0

J ^(ⁿ *) = Mn ) ⁺ M * (u * ) ⁺ 7 * ( ^v i ) - 1 i * j

I j n + 1) = j n *) + H j ( v _h )

j = 1,2,L, N , h

In the equation, v _h ( n ) refers to the time of the CH’s transmission service for the information packets at the key node, while n j ( v h ) , the information packets entering the memory of the j node at the time of v_h

Based on the above operational process, the status of the polling system can be described by Markov Chain which is noncyclical and ergodic. Stable state is there on N condition of ^ pi + ph = Np + ph < 1

(With P i = A i eP h = pA„P_h , i = 1,2, L , N )

When the CH polls at the key node at the time of t_n ^* , the probability generating function of system status is illustrated as:

G (z , z , L , z , z ) = lim£ ih 1     2            N h t ^1»

^N     J ( ⁿ * )     J ( ⁿ * )

ih

П z? zh i=1

N

= R.(Z Ak (1 - zt ) + A (1 - zh)){— Bid \ (1 - z, ) + A, (1 - zh)) • k=1                                                 zij

[G (z , z ,L , z , z ) - G (z ,z ,L , z , z )|]

^L i ' I ’   2 ’      ’ N ’ h'          t ' I ’   2 ’      ’ N ’ h ' | zi =0 ^J

+G(z ,z ,L ,z ,z )| } i ' I ’   2 ’       ’ N ’ h ' | zi =0 ’

When the server polls at the i + 1 station at the time of t n _{+ 1} , the probability generating function of system status is:

N       (n+1)(

G*+1(z1, z 2,L, zN, zh) = limE П zi*

t ^м     L i=1

N

= % ( z _pL , z n , Hh £ A _k (1 - z k )))

k = 1

With H , ( - ) = B $ + A h (1 - H h ( $ )))

• D.    The Analysis of Mean Queue Length

Given that g. (j) is the average number of information packets number at the j node buffer when the i node starts service at the time oftn , then

( A_              ^d G i ⁽ z 1 , z 2 ^{, l}, z n , z h )

gi-(j) =    lim ----------------------- z Л, zn ■ zh ^1          5zj i = 1,2,L N, h ; j = 1,2,L N, h

When the CH starts its service for the i node, the average information packets stored in the memory of the i node are g%i ( i ) . Then, the mean queuing length of the common nodes can be calculated with the first-order local derivation via (1) and (2) equations:

Ш                          ^d G i + 1 ⁽ z 1 , z 2 ,^L , z n , z , )

g+1( j,h ) =    lim --------------------- z 1Lzn - z, ^*         5z, 5z,

= R (0) A j pA h (1 + h h )² + rp 2A_hA_}A_hHh_h ’(0)

+ 2 rA j pA h (1 + h %> , )² P i (1 - GG_t 0 ) + rA j (1 + h %- , ) j g ? ( h ) + rA h (1 + h %» , ) ^ g i ( j ) + 2 B % i \0)A_] p A_h (1 + h %» , )²(1 - ( G i 0 ) + p i p 2 AAA_!kiH^,h ’ (0)(1 - GG i 0 ) + e i A [ ^ g i ( h ) - j g i 0 ( h )] + P i p A h (1 + h%» , )[ g ( j ) - g ₀( j )] + g ( j , h ), i * j * h

（ 3 ）

^g i + 1 ( j , i )

^d 2 G i + 1 ( z 1 , z 2 ^{, L} , z n , z h

= lim ------------------ z 1-L-zn - zh ^1           gzjgzi

= R%-, (0) AA j (1 + h h ) 2 + rpA hA^'h '(0)

+2 rAA j (1 + h h )² p i (1 - G i 0 ) + 2A,(1 + h h )( _Z i + p i ) ^ g i ( i )

+ r i (1+/%)( Y + p i )^ g i ( j )+ B% i (0) AA j (1+/%) (1 - G i 0 )

+2PAA ₃ pA cf H X0)(1 - ( G i 0 ) - ^ g i ( j )+j g i 0 ( j )

+ p * a * (1+ h% )^ g i 0 ( j ) - a , (1+ h e )(1 - ( G i 0 )+^ g i ( j , i )

, i * j ( 4 )

gk +1^{( j} , ^j ) =     lim

^TAr,?" 7.^1

z1 zN zh d G*+1(z 1, z2,L , zn, zh)

d z j d z j

= R % ^ (0) A /(1 + h h )² + r i pA h A j² fH h ’(0)

+ 2 rA j (1 + h h ) p * (1 - GG * ₀) + т * А , (1 + h h )j g * ( j )

+ 2JB - (0) A j ²(1 + h h )²(1 - GG * ₀) + p i pA h A j ^H h ’ (0)(1 - GG * 0 )

+ 2 PA ₃ (1 + h h )[j g * ( j ) - ^ g * ₀( j )] +^ g * ( j , j ), * * j

^g.+1( *, *) -     lim zv'-zn , zh ^1

^d G. ⁽ z 1 , z 2 ,^L , z n , z h )

* +1 ^{x                          7}

d z * d z *

= J R *(0) A * ²(1 + h h )² + r-pA hA² H ’(0)

+ 2 rA * ² (1 + h h )² p * (1 - G * 0 ) + 2 A j (1 + h h )( Y + p i ) g ( j )

+ B i (0) A (1 + h h ) (1 - ( G i 0 ) - pA h A*²GH h ’ (0)(1 - G 0 )

+ g ( i , i ) - 2 A * (1 + h h )(1 - ( G i 0 ) + (1 - GG * 0 ) - g ( i )

（ 6 ）

Under the condition of the symmetrical parameters, g i * ( i ) can be derived as the following via above equations:

z                 ^d G i ( z i , z 2 , L , z n , Z h )

g(i) =   lim -------------------- z/Lz.z. ^           dz,

Nr λ ²                 _•

⁼ 2(1 - ρ _h )(1 - ρ _h - N ρ )(1 - ρ _h - N λ ( γ + β )

{(1 - p_h - N p ) R (0) + A h B* (0) + N A, B* (0) r

+ 2 Nr ρ - ( N - 3) r ρ _h - ( N + 1) γ

+ 2(1 - ρ _h )(1 - ρ _h - N ρ )/ λ }

（ 7 ）

With

e h = - B h (0), H‘ (0) = - -&-,

1 - ρ _h

*h№=tb^h =- *h (0)

(1-ρh)3

When the CH polls at the key node the average information packets stored in the memory of the key node are gh (h). Likewise, the mean queuing length of the key node can be calculated in the same way:

% ( h ) ==

lim

^d G h ⁽ z 1 , z 2 , L , z . , z h )

Z ^{, L ,} 7 ^, 7 ^ 1 1    z N z h

∂ z h

= pλ_h ( r_i +

^ρ i ∑ ^rk   ₎

1 - ρ_h - ∑ ρ_k

• E.    The Analysis of the Mean Inquiry Cycle

Based on the operational mechanism of the system and the theory of queuing, the mean inquiry cycle can be derived as:

E [ θ _i ] =

∑ r k

1 - ρ _h - ∑ ρ _k

• F.    The Mean Delay Time of Information Packets

The average time delay of information packets refers to the period during which information packets enter the memory of the node and then wait to be served. With reference to the calculation of Note [8], the system’s average time delay can be obtained via second-order local derivation of the system status.

The average time delay of the lower priority information packets at the common node is:

%() 1

E ⁽ w’=1 2 ^9 " X               ^{( 10 )}

The average time delay of the higher information packets at the key node is:

, ,   %h ( h , h )    ряД (0)

Ew =      +

^{( h} )   2 p X h % h ( h )   2(1 - p h )

priority

（ 11 ）

With g% h(h,h)=R% (0)p2λh2+R% (0)B% (0) p2λh2λiθ% +B% (0)p2λh2λiθ% Theoretical Calculation, Simulated Experiment and

Analysis

Both theoretical and simulated models are set in identical symmetrical conditions under which each node’s information packets arrival follows the Poisson distribution with λ as the parameter, and all the node parameters follow the distribution of identical laws. The time slot width is taken as 15 ^µ s , with the length of information packets being 8100bits. With N =9 , β _h = β = 10 , λ _h = λ = λ , γ =1 , the

N system meets the stable condition of ∑ ρ + ρh < 1 . The =1

data in the following charts show that the theoretical value of the system model in this research correspond well with that of the experiment and it can represent the first order feature of the system.

• 1)    Considering the system model and operation mechanism, Fig.2 shows that the key node gets 2 N times exhaustive-service in a polling cycle, so that access channel opportunities and transmission quality get more priority guarantee.

• 2)    Fig.3 reveals the tendency that the mean queuing length of both key and common nodes changes along with the variations of the number of system nodes and their arrival rate, which in turn shows that the main queuing length of the key node has been clearly differentiated from that of the common nodes. With the increase of the common node number ( N ) and the arrival rate ( λ ), the mean queuing length of the key node is much smaller than that of the common nodes. In other words, the central node enjoys a smaller mean queuing length. Fig.6 shows that the mean queue length of key queue has been markedly less. So, efficiency of the key node is enhanced. That is to say, the information packets take up less of the node’s buffer. The communication between the different clusters more efficiently. Overall, energy consumption of Wireless transmission between the different clusters can be effectively reduced.

• 3)    Fig. 4 reveals the tendency that the mean queuing delay duration of both the high-and-low priority nodes changes along with the variations of the number of system nodes and arrival rate, which in turn shows that the mean queuing delay duration of the high- priority node has been clearly differentiated from that of the low-priority nodes, identical to the case of the mean queuing length. With the increase of the common node number ( N ) and the arrival rate ( λ ),the mean queuing delay duration of the high-priority node is much lower than that of the low-priority nodes, and the former maintains greater stability. Transmission quality of packets from upstream cluster gets better guaranteed.

• 4)    Fig.5 reveals that each node in the system enjoys identical mean cycle period and that the system’s mean inquiry cycle is greatly influenced by the number of nodes

  since the average inquiry cycle increases rapidly along with the increase of the number of nodes.

  

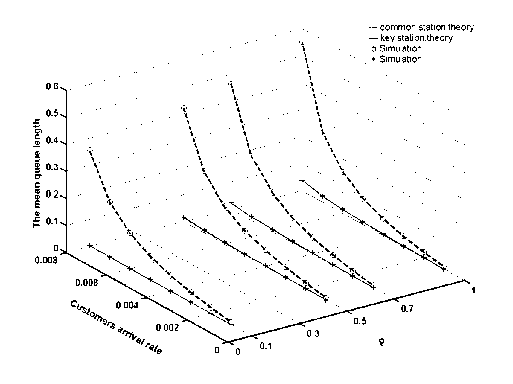
  Figure 3. The mean queue length

  
  

and QoS guaranteeing. This efficient scheme embodies the advantages of exhaustive and limited policy service, and it classifies the system nodes by priority at two levels to enhance the fairness and flexibility of the service system. The higher-priority key node applies an exhaustive-service policy with more opportunities for routing so that transmission quality between the different clusters gets better guaranteed.

The theoretical model for the scheduling algorithm is established on condition of stability, and by means of Markov chain, multidimensional probability generating function. The findings of theoretical calculation correspond well with those of simulated experiments. The theoretical and simulated findings all reveal that system performance can achieve the optimization effect. It concludes that this scheme enables WSNs to take on the features of good utility, good function.

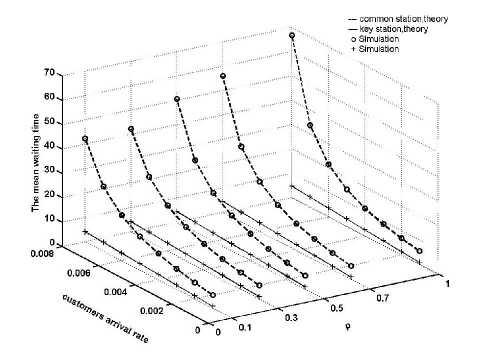
Figure 4. The Mean Delay Time of Information Packets

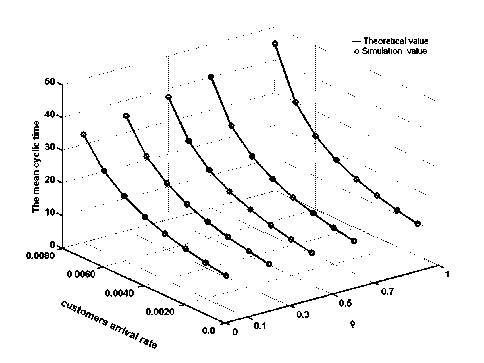
Figure 5. The mean cyclic time of the system

III. C ONCLUSION

In this paper, research work was done on a MAC scheme in WSNs has been done with focus on energy efficiency

A CKNOWLEDGMENTS

Our sincere thanks go to Professor Zha Guangming of UESTC! The authors would like to give their sincere thanks to the financial support by the Nation Natural Science Foundation of China (No.61072079)