A Secure and Efficient Cryptography System Based on Chaotic Maps for Securing Data Image in Fog Computing

The expansion of the Internet of Things (IOT) has led to mass production Data, with massive computing resources, storage space and communication bandwidth. The IOT realizes the interconnection of mature technology equipment from home to vehicle and workplace [1]. So, the term fog computing has emerged as horizontal intermediate layer between a cloud data centers and IOT devices that distributes storage, computing and data processing nearer to the end users [2]. Fog computing was first introduced by cisco and by pooling available computing, storage, and network resources at the edge of the network, service delivery is closer to the end user [1, 3]. It is a decentralized computing infrastructure, using one or more IOT collaborative execution on devices or edge devices close to the user a lot of communication, control, storage and management. Through the fog node and equipment, fog computing can reduce processing burden Resource-constrained equipment meets latency requirements delay sensitive applications and overcome bandwidth constraints of centralized services [4].In addition to it, fog computing also provides; (1) support for high mobility, (2) high responsiveness computation resources, (3) different communication protocols, (4) multiple data sources and devices can be integrated and moreover heterogeneity of interface within infrastructure, and (5) interoperability which must be able to interoperate and cooperate with different providers with wide range of services and effortlessly support certain services [5].

However, fog computing has not overcome the threats and security weaknesses that it is still exposed to in its system, which may have a significant impact on the system behavior and its exposure to breach and data exposure to repeated risks due to the lack of permanent stability against security issues, and therefore it is necessary to provide the most Effective solutions that resist these security issues, reduce risks to devices, and provide a strong and secure medium for data [1]. “Fig. 1,” shows fog computing architecture.

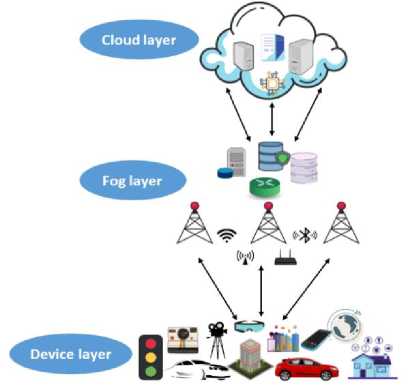
Fig.1. Fog Computing Structure Graph.

Digital image measures utilized in many applications as medical image, and image knowledge base of this digital image have to be compelled to be defend from unauthorized. A significant amount of this data image is private and should remain confidential between the exchanging parties, therefore, most of the ISP's reliance is on encryption and decryption techniques [6]. However, as a result of unlawful wiretapping, revision, or interception, there's a visible lack of security for communication images over the network, significantly [7-9]. Moreover, there're numerous means and tracks in which to emphasize the transference of secured data that compared to other strategies to ensure the safety of images as in medical field as one of the important areas against unauthorized access [7, 9].

Chaos- based secret techniques are thought of to be the foremost necessary because the wonderful features of chaotic system which can pledge the speed and high security [10]. Chaos-depended techniques have lately turn into appealing for shielding image content. Chaotic systems are sensitive, non-liner, deterministic and easy to reconstruct after filling in the image. Use their topmost characteristics like management control parameter, sensitivity to the initial condition, and non-convergence during a chaotic system (or map). Several schemes of image encryption have been proposed using Chaos and their worthiness has been partially demonstrated [11]. The overview of the related work revealed that chaotic systems have been exploited for efficient for multimedia data encryption. In cryptography, having a secure routing is needful to cross data through a secure lines and networks. Chaotic cryptosystem is one of the methods are thought of to be to be one of the essential element necessary because the effective properties of chaotic system which is sensitive, non-liner, deterministic and easy to reconstruct after filling in the image [9].Image encryption process can be categorized as i) position permutation, ii) value transformation. In the first technique it happens permutation for the image position with no changing in the pixel value of the image, and in second technique pixel value is substituted by another with no changing in the image position [12].

2.    Related Works

Lately a lot of research represent many schemes of image encryption which is used the cryptosystem of chaotic theory to obtain the strength and the preferable image encryption techniques, here, we will explain and mention some of the research that was presented and received interest in this part. Arwa et al. [13], proposed a technique which based on pixel shuffling starting by converting the pixel value from a three-dimensional value (R, G, B) to 1D, then generate a row vector from image pixel and make a random permutation of row vector. XOR operation is obtained and finally 3D chaotic map is performed, it is limited by losing some data in the decryption process because of using 3D value of image in encryption steps and restored with 1D value in decryption stage. Yasser et al. [10] suggested hybrid method which the chaotic maps are combined, the author based on the technique of Discrete Wavelet Transform (DWT) and disband the image it to sub-bands. Both confusion and diffusion have procedured in the system. Assorts of chaotic maps types could be related to the image to enhance the encryption process. In recent period a lot of authors are turning to the field of using DNA technique, Shuqin et al. [14] characterized an algorithm that is depend on 5D continuous and chaotic system hybrid type, which adopts DNA dynamic coding mechanism and scrambling process with two rounds of diffusion encryption structure to enhance the security, the weakness point that the ability of cipher text to resist noise, cut and compress attacks is weak , also the more dimensional process used the more complexity and heavy cost will be. Many research has been proposed algorithms depend on scan patterns techniques. Mura Mural, P et al [15] designed a scheme based on Space Filling Curve that make the image scrambled using the mechanism of square wave to obtain confusion with many orders and diffused as well using saw-tooth technique with some various orders. The author doesn't use any chaotic equation or system in his proposed system to achieve confusion and diffusion. Another scheme for image encryption, Zhang, Xuncai, et al [16] this algorithm used a scheme of cryptography that depend on hybrid of Hilbert curve and H-fractal to realize the techniques of confusion and diffusion that achieved scrambling and value exchanging operations. In this work the sequence generator is based on both the piece-wise linear chaotic map (PWLCM) and Rossler chaotic. Shahna, K. U.et. al [17] proposes an encryption technique using Logistic map and Z-order curve, pixel scrambling is performed using Z-order curve and random matrix is generated using Logistic map and the results show us that the system does not have a high quality of security and vulnerable. Fu, C.et. al [7] suggested a technique which is bit permutation to overcome the drawbacks of conventional permutation-only type image cipher a significant diffusion effect in permutation procedure through a two-stage bit-level shuffling, scheme has a comparable security level and a much lower computational complexity.

3.    Problem Statement

As it was mentioned previously, the encryption of data images is one of the most important issues that must be highlighted and worked to improve and develop in a superior manner, so we are trying to develop a solution to establish a secure and effective encryption system. The major purpose of our project is providing an effective and powerful mechanism to secure image data through an encryption system based on chaotic maps that has results of high sensitivity and quality level, moreover the used of scan patterns properties as the results based on this work showed the effectiveness of the system and its impact on encryption and the difficulty of being exposed to the attacks.

Usually, the cryptography processes which depend on chaotic techniques consists of two main ways includes confusion and diffusion, scrambling is the core meaning of confusion stage, the one that handle with pixels position, while diffusion technology is a technique for pixel value changing and diffuse pixels that has impact of changing the values of another pixel. And here in our proposed algorithm we use a hybrid between both confusion and diffusion in order to enhance and have a high quality of security system. To realize the scrambling operation, we use the Hilbert curve, as considered as popular and it's widely used in many applications because of its continuity as a continuously mapping, scalability and stability as the level increases, the distance of each point on the graph will become smaller and smaller, and as the level increases, the graphics will become more and more the larger, the point movement becomes no longer important. So, it can be regarded as no movement. Besides that, it's worth for mention that Henon map is a good chaotic map that its trajectory of it is simple and have something determined, thus the maps can be easily predicted with super quality plus it has superior features in generating perfect random sequence with regularly and constant allocation. The proposed system ensures high quality of resistance with better security cryptosystem due to both confusion and diffusion technology through two times of scrambling, once for pixel permutation, and another for value permutation using cyclic bit shifting technique. Now we can define the main and effective contributions of this paper in an understandable and summary form:

• -    The proposed system in our work uses bit permutation for realizing diffusion and the confusion can be actioned through applying pixel permutation mechanism.

• -    In this scheme, the Henon chaotic map is 2D which is more efficient and used for the generation of permutation sequences for realizing diffusion.

• -    The Hilbert curve is used for the generation of masking sequences for realizing confusion.

• -    The approached work proved that cipher image with high keys sensitivity with any changes in the original image.

• -    The outcome of the proposed algorithm is compared with existing results and validated by different cryptanalysis through many performance evaluation metrics that are usually used to evaluate the efficiency of image encryption approaches.

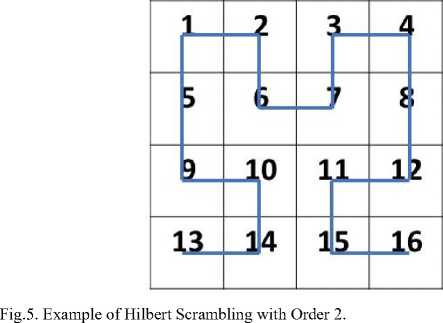
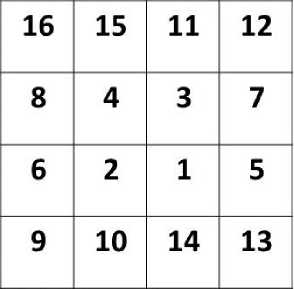
4.    Block Diagram of the Proposed System 4.1.    Hilbert Scrambling (Space Filling Curve)

There are some experiments, tests and comparisons that are presented to prove the performance of the proposed system algorithm.

The residuum of this paper is orderly as follows: Section 4 shows flowchart of the proposed system and the proposed approach fully explained below in “Fig. 2,” Section 5 and section 6 discusses the results and the analysis of our results. Conclusion and future works are given in Section 7.

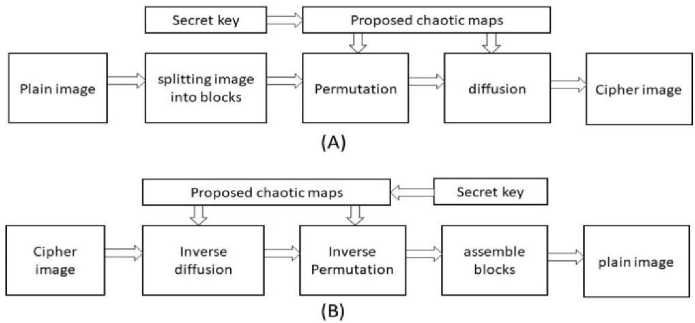
Fig.2. Proposed System Flowchart.

The Hilbert curve is a continuous fractal space-filling curve first described by the German mathematician David Hilbert in 1891 [16]. Hilbert curve is used to make a shuffling process of the pixels position of the original image to get a new scrambled image. According to the characteristics of its own space filling curve, the Hilbert curve can linearly traverse each discrete unit in two dimensions or higher dimensions, and only traverse once, and linearly sort and code each discrete unit, which is the only one of the unit Logo. Since the Hilbert code does not have a large step jump, the aggregation performance of the Hilbert space arrangement is better, that is, the adjacent points on the Hilbert curve must be adjacent in the original space. The Hilbert curve is an FASS curve, that is, space-filling, self-avoiding, selfsimilar, and simple one. These curves are situated in a Euclidean space and have a dimension higher than 1 and have non-hollow internal in the space [16].

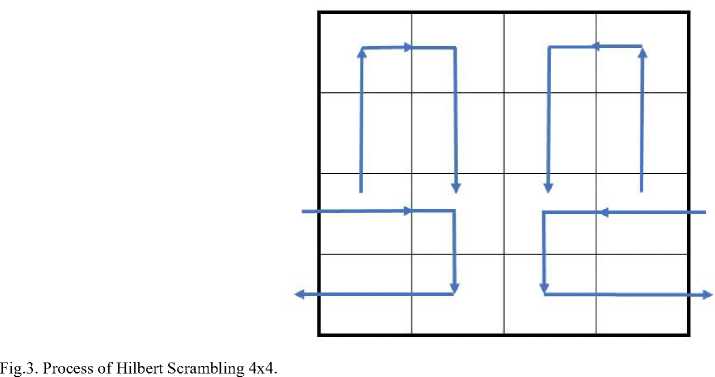
Now we will discuss the first iteration / order of Hilbert curve: the main square is splatted into four parts each part is as mini square starting the curve from the square's center in the southwest then to the square's center in the northwest corner heading to the square's center in northeast ending to the square's center of southeast, here we finished the main cycle, The places of the beginning stage and the ending point of the Hilbert curve refer to the direction of it [16], “Fig. 3,”refer to the description of Hilbert curve process.

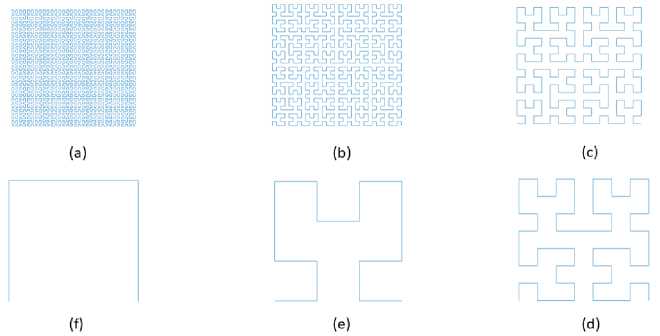
Fig.4. Hilbert Curve Shapes where Fig (a) Refer to Order 6, Fig(b) Refer to Order 5, Fig (c) Refer to Order 4, Fig (d) Refer to Order 3, Fig (e) Refer to Order 2, Fig (f) Refer to Order 1.

• 4.2.    Henon Map

It is a discrete-time dynamical system. It is one of the most studied examples of dynamical systems that exhibit chaotic behavior [21]. The Henon map takes a point (xn,yn) in the plane and maps it to a new point. The map was introduced by Michel Hénon as a simplified model of the Poincaré section of the Lorenz model, using the following equations: - xn+1 = 1 - «xn 2 + Уп

У п + 1 = ^x n

There're two main parameters the Henon map is based on, for the standard Henon map have values of α = 1.4 and β = 0.3. For these classical values the Henon map considered as chaotic, the graph of this map is obtained in “Fig. 6,” Also the simulation of Henon bifurcation map of a chaotic diagram is shown in “Fig. 8& 9,”. Bifurcation diagram plots output sequences of a chaotic map along with the change of its system parameter(s) [22]. From the bifurcation diagram in “Fig. 8&9,” it is clear that Henon map is chaotic for the range of parameter (a) 1 ∈ [1.06, 1.22] ∪ [1.27, 1.29] ∪ [1.31, 1.4] [22]. Moreover, Chaotic motion is very sensitive to initial conditions and lyapunov gives a set of values called ( X ) where one of the values of it must be positive and this means that the system is chaos and has a chaotic movement as we see in “Fig. 7,” when the chaotic system is extremely very small in two different differential its motion path progressively generates indicator separation.

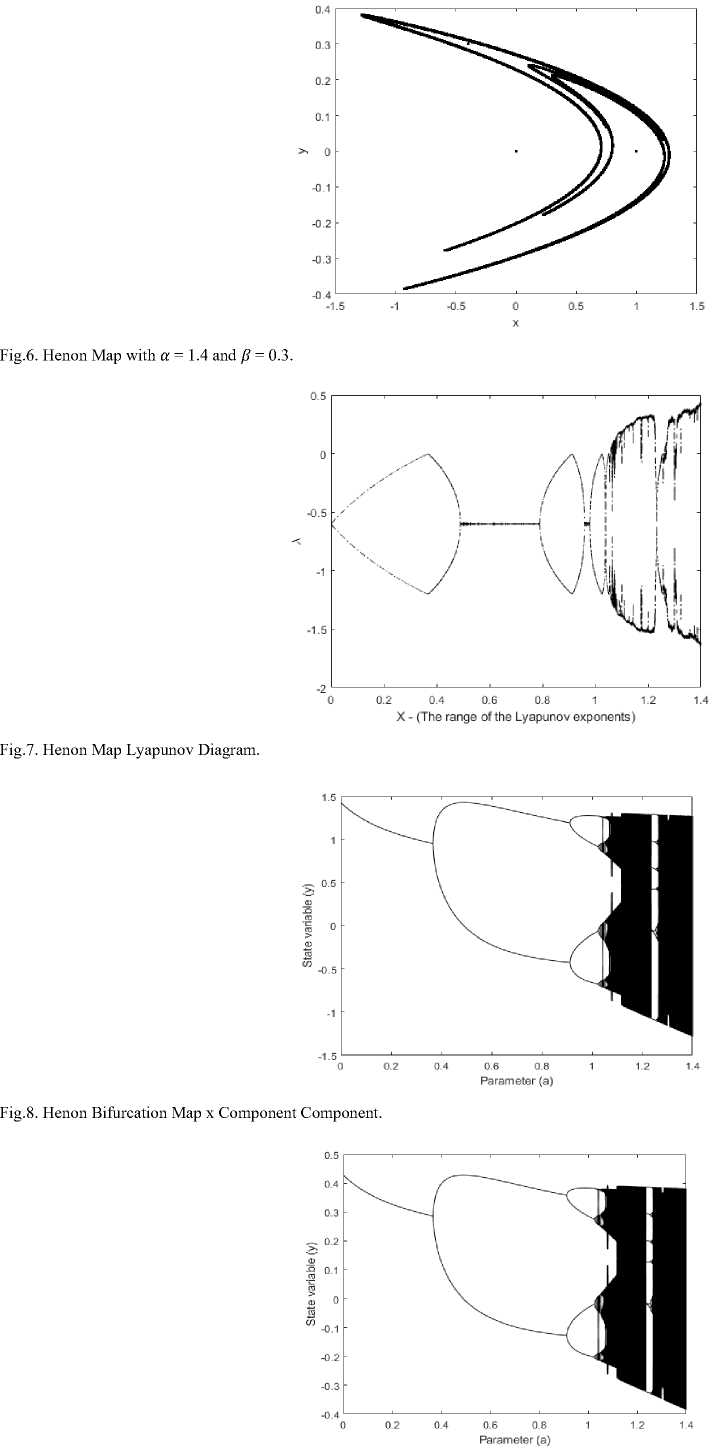
Fig.9. Henon Bifurcation Map y Component.

• 4.3.    Encryption Algorithm Steps

The proposed cryptosystem starts with dividing the plain image into blocks then shuffling the pixels of this blocks indices with Hilbert maps key generation, then these shuffles blocks goes through two further encryption steps to strengthen algorithm, the first step is scrambling the images in a confusion process using the key generation of Hilbert scan then the diffusion step which takes the output of the confusion step and performs pixel value alterations based on the Henon map, the Henon maps follows the Henon formulas for generation of the keys the diffusion performs the encryption by altering the current pixel value based on the previous pixel to create a more robust encryption. The decryption process is done by a process of reversing all the previous steps in the encryption process to get the original image again and perform all the steps in order to get the original version of the data as we see below in details:

Our Proposed Algorithm Procedure:

1-Read the plain image (PI) with the size (W × H) where W and H respectively, are width and height of the plain image pixels.

2-Splitting the plain image (PI) into blocks.

3-Shuffling the blocks by Hilbert key generation.

• 4-    Generating “Henon key” for each block separately as in the following: -

  Г a1 = 0.00000012547

Initial values of Henon map

I bl = 0.00006122 I

Popularize parameters with introducing their initial values: - ai = 0.000001235544789, b = 0.003578891472566, u = 73834772913855, p = 71277967533485

Now upgrading values by these following equations:

u = u + floor(e2П *105)(3)

Here we get:

51 = ^*256 - e2n

v p = p + floor ([S1]*105)(5)

Here we get:

52 = ((X1 *107) - floor(X1 *107))(6)

which;

a = a 1 + ((51 - floor(S1)) *10-5)(7)

b = b1 +

• -    The new values of a₁& b₁ is presented for repetition henon map (t=500).

• -    Now, two chaotic sequences is obtained x , y.

• -    Through the upgrading of a₁& b₁ , process the chaotic sequence to get sequences of C1 & C2 by the equations below:

C1 = [ C 1, round (mod(( x ²) - floor ( x ² ) u *10⁹,255) + 1)]                          (9)

C 2 = [ C 2, round (mod((y²) - floor (y² )p*10⁹,255) + 1)]                       (10)

	x = 1 - a x2 + y                                         (11) y = в * У                                            (12)
- Then we get the two Henon keys:	Key1 = (C1(t + 1end),[M,N])                                      (13) Key 2 = (C2(t + 1end),[M,N])                                   (14)

Which [M, N] is considered as key size.

5-Then the scrambling step:

• 1)    First according to the Hilbert curve mechanism set up the Hilbert pattern due to the description that mentioned above, “Fig. 4,” shows the different orders of Hilbert scrambling curve. ii) second iterate every pixel in the shuffled image from the step 3 in order to get the whole bits and represented in a matrix form (Matrix A), iii) third as the same way of second step, recur the values of the key1 in “(13),” and represented in a matrix form as the size of the key1 (Matrix B).

Fig.10. Example of Shifting Bits Process Mechanism.

6-here we get the confusion form of the encrypted image using Key1 and represented a new matrix after completing several procedures on the image to obtain an opaque version that does not have any clear features, let's named it by (IMG).

7-The key2 which is generated in “(14),” is used in this step which is called diffusion step.

G 1 = [mod IMG + U + V , 255] XORKey 2(1)]	(15)
G1i+! = {mod G1 + IMGi+ , + V ,255] XORKey 2/+1]	(16)

Where: i=1,2,…

• 8-    Now, after the final encryption process, the decryption on the other hand reverses all of these steps backwards, it starts by inverting the diffusion step using the same key used for encryption, then it reverses to the encryption step and restores the pixels indices caused by confusion using the same Hilbert maps as in the encryption step and finally assembling the blocks to return to the plain version of the data.

5.    Performance Metrics

• 5.1.    Histogram Analysis

• 5.2.    Correlation Analysis

IMG = mod[ XORG1(1),Key (1) - r - v )255]

IMG_i+ j = mod[ XORG1_i+1 , Key2_i+ j - G 1(1) - r , 255]

There are some performance measures that we use to get to know the impact of the proposed system and its effectiveness in achieving the best expected results from its performance, through some several parameters which cover the statistical, differential and efficiencies metrics.

This histogram is a graph that describes the graphical representation of the image and it is showing the number of pixels in an image at each different intensity value found in that image [20].

Correlation measures the degree of matching between two adjacent pixels of an image [23]. For the image in naturally, there is usually a high degree of correlation in most cases Due to pixel continuity, adjacent pixel pairs [24]. The following equation used for correlation calculation coefficient, the correlation of the original and encrypted images of our proposed system:

_r=   E i N^ x i ^- x ⁾⁽y i ^- y )

V E Z/x - ^{- x )2(}y . ^- y ) 2

r = Correlation coefficient, X / = values of the x-variable in a sample, x =mean of the values of the x-variable, y =values of variable in a sample, y =mean of the values of the y-variable.

• 5.3.    Information Entropy Analysis

• 5.4.    Mean Square Error

It is a statistical merit for gauging the randomness's degree [25], and it describes the confusion properties of the original and the cipher image.

The ideal value is always equal to 8 for which the pixel values of the image always fall in the range of 0-255 [26]. The entropy value may fluctuate for the various pixel values of the image falls. Hence the suggested cryptosystem has 256 states so the maximum information entropy will be approached to 8 [7]. The following equation Used to calculate the information entropy:

2 l - 1

H ⁽ m ) = -Ei = 0 P ⁽ m i ^)log 2 ⁽ P ⁽ m i ))                                      ⁽²⁰⁾

Where L indication to the total number of pixels values, p(m / ) is refers to the probability to m / .

As we can see, the above statistical parameters have a strong influence in judging the robustness and resistance of the proposed system towards any screening, in order to ensure that it enjoys a robust encryption level.

It measures the variation of two images. When its result is low that's indication to the less of the variation between both original and encrypted image [10].

MSE =

1 m_xn_xf

fmn

EEE ( P(i,j ) - c(i,j ))² k = 1 i = 1 j = 1

Where p(i,j) is mentioned for original image, c(i,f) is mentioned for encrypted image, m, n is mentioned for total number of rows and columns.

• 5.5.    Peak Signal-to-Noise Ratio

• 5.6.    Number of Pixels Change Rate

PSNR is measuring the ratio and the conformity between original and encrypted image [27].

PSNR = 10log₁₀( Max ⁰¹- ) dB

¹⁰ MSE

Where Max01 refer to the max conceivable pixel value of the original image.

NPCR is used to measure the change rate of pixel's number of encrypted image when adjusting a pixel in the original image [10].

NPCR =

MxN

E i,j D ( i , j ) X 100%

Where J 0,^D1(i,j) = ^D2(i,j) | [ 1,D1(i,j) * D2(i,j) J

• 5.7.    Unified Average Changing Intensity

UACI is for the average change intensity of differences between both original and ciphered images [28].

UACI = £

I D1( i , j ) - D 2( i , j )|"

J——-- X 100%

MNx 255

Where N, M is referred to the columns and rows respectively, D2 is decrypted image, and D1 is the original image. In this part, we will make a comparison between our proposed system and the other different algorithms through the results of NPCR and UACI that ensure our proposed system accomplished a better result compared to the others.

When analyzing the influence on the system in terms of its sensitivity and flexibility towards the attacker changing some features of the original image to obtain a difference in the content of the encrypted image, the need for the availability of differential parameters (the above mentioned) to maintain such attacks will protect the system from activating or forming any changes by any stranger. So, these differential aggressions will not be of any use.

Therefore, performance measures dominate very much in influencing the strength of the system and the extent of the impact of each parameter separately, and therefore the rigidity of the system is subject to such parameters to know the difference between the effect of routine methods and the proposed system. In Table 1 it's shown the various parameters that illustrate the analysis of the effectiveness of performance measures in our system, with a mention of the speed of performance in terms of time, as it is one of the most important parameter that reflect efficiency, especially with regard to real-time applications.

40    60    80   100   120   140   160   180 200   220               40   60   80   100 120 140 160 180 200 220 240

40    60    80   100   120   140   160   180   200   220                40   60    80   100  120  140  160  180  200 220  240

(b)                                                (e)

Table 1. The factors of the Encryption Goodness for Some Various Image Tested.

Images	Entropy	PSNR	T(sec)	MSE
cameraman	7.9992	8.4061	0.219399	9385.717
Baboon	7.9993	9.8148	0.14299	6785.7811
Peppers	7.9993	8.256	0.18481	9715.8455
Lena	7.9993	9.2376	0.17867	7750.3625
Mean	7.999275	8.928625	0.18147225	8409.426525

Table 2. Refers to the Parameters of NPCR (%) and UACI (%) of our Proposed System.

Images Parameters	Cameraman	Baboon	Peppers	Lena
NPCR (%)	99.6779	99.6908	99.5376	99.6908
UACI (%)	33.6204	33.6247	33.5736	33.6247

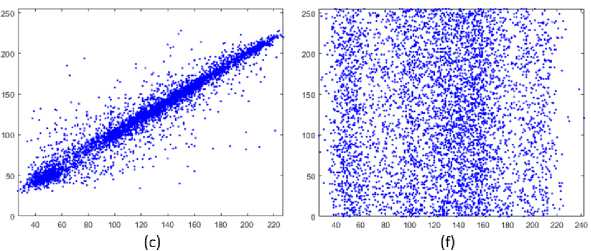
Table 3. Correlation Coefficient of the Original Images and their Encrypted Images.

Images	Directions	Horizontal	Vertical	Diagonal
cameraman	Plain image cipher image	0.98448 -0.016364	0.99074 0.0048909	0.97558 -0.0082512
Baboon	Plain image cipher image	0.98075 0.0094014	0.97453 -0.030857	0.95822 0.0058893
Peppers	Plain image cipher image	0.97767 -0.018014	0.97125 -0.00072265	0.97886 -0.020445
Lena	Plain image cipher image	0.97576 -0.0025414	0.98412 0.00091759	0.96208 -0.0019035

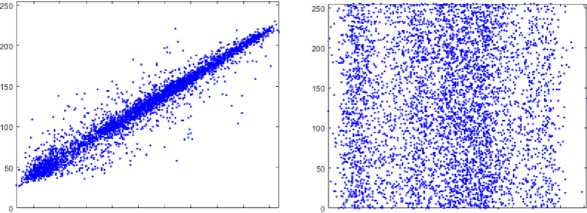
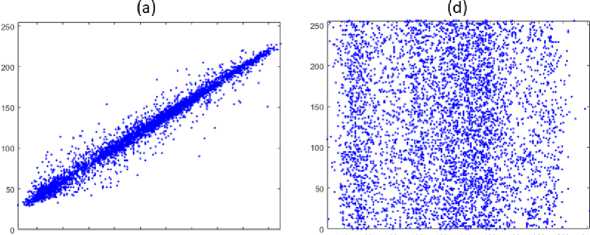
For an image there's adjacent pixels have some degrees of correlation in horizontal, vertical and diagonal directions, so it can be seemed that in the original image the correlation is very vigorous regarding to the linearity linkage in all directions and it has a high correlation while the ciphered image has a very low one with random shape. In order to obtain an excellent cryptography algorithm to conserve the data from attackers whom manage statistical onslaught by exploiting correlation values of the original image, therefore it supposed to breakdown this linkage in the encrypted image. from Table 3, it's clear that the correlation value of plain image is close to value 1 and that's refer to the strength of its adjacent pixel correlation, and the opposite for the correlation value of encrypted image is close to value 0 which means the adjacent pixel correlation is extremely weak, and for the negative values it's confirming that there's no rapport between the original and the encrypted image. “Fig. 11,” refer to the simulation of correlation in our proposed algorithm.

Table 4. The Parameters of NPCR (%) and UACI (%) of our Proposed System Compared to another References.