A Secure and Robust Image Encryption Scheme Based on Mixture of Multiple Generalized Bernoulli Shift Maps and Arnold Maps

not suitable for practical digital image encryption due to the weakness of low-level efficiency while encrypting images. Fortunately, chaos-based image encryption algorithms have shown their superior performance [4-8]. Chaotic maps can simulate random behavior in a quite impressive way. In particular, chaotic maps are easy to be implemented by microprocessors and personal computers. Therefore, chaotic cryptosystems generally have high speed with low cost, which makes them better candidates than many traditional ciphers for multimedia data encryption.

Among the chaos-based encryption schemes, onedimensional and two-dimensional chaotic systems, such as logistic map [8,9], skew tent map [10], Arnold map [7,11], baker map [4], piecewise linear chaotic map [12,13], piecewise nonlinear chaotic maps [14] and standard map [15-17], were applied widely owing to the advantage of simple implementation. However, there are fundamental drawbacks in these chaotic systems, such as small key space, slow performance speed and weak security. As a matter of fact, some chaos-based image encryption algorithms have been broken recently [18-22]. To overcome the aforementioned drawbacks, a novel chaos-based image encryption scheme based on combination of multiple chaotic systems is constructed in this paper. The mixture of several chaotic maps possesses a significant achievement because of the following special inherent features. Firstly, it is well known that any chaotic orbit will eventually become periodic in computer realizations with a finite precision. However, for a hybrid chaotic system consisting of multiple chaotic maps, these periods turn to be so long that one can observe only aperiodicity in almost any realistic application. Secondly, the combination enhances the security of the proposed encryption scheme significantly.

The proposed image encryption scheme here consists of a permutation process and a diffusion process. Thanks to the simplicity of generalized Bernoulli shift maps, we choose them as the candidates of chaotic maps utilized in both the permutation process and the diffusion process. Six generalized Bernoulli shift maps are utilized to generate one hybrid chaotic orbit by one six-dimensional Arnold map and then applied to scramble the pixel positions in the permutation process, while four generalized Bernoulli shift maps and one Arnold map are employed to yield two pseudo-random gray value sequences to change the gray values by a two-way diffusion process. Although six generalized Bernoulli shift maps are used in the permutation process, the computation overhead is almost the same as that caused by one generalized Bernoulli shift map. The reason is that the total iteration times for the six generalized Bernoulli shift maps are the same as those for one generalized Bernoulli shift map if the few transient iteration times are not considered. To improve the sensitivity of the control parameters and initial conditions, high dimensional Arnold map is employed to integrate the chaotic effects of the multiple generalized Bernoulli shift maps. Thanks to the good permutation–diffusion mechanism, the proposed image encryption scheme possesses a huge key space with capacity 10320 , therefore efficiently frustrating brute-force attack. Experimental results are carried out with detailed analysis to demonstrate also possesses good statistical properties to frustrate statistical, differential attacks. An additional merit for the proposed scheme is its robustness against malicious attacks on the cipherimages. As far as we know, many image encryption schemes are vulnerable to image processing, such as cropping, noising, compression, etc. The robustness against such a kind of image processing is also important for cryptosystems. The opponents would rather tamper the cipher-images than analyze them as they are not able to perform the cryptanalysis. The robustness test of the proposed scheme against malicious attacks, like cropping, noising, JPEG compression, is then performed as well. All the satisfactory properties make the proposed image encryption scheme a potential candidate for practical image encryption.

The rest of the paper is organized as follows. In Section II, generalized Bernoulli shift map and Arnold map are reviewed briefly. Section III proposes a novel image encryption scheme composed of one permutation process and one diffusion process based on generalized Bernoulli shift maps and Arnold maps. The security of the proposed scheme is evaluated via detailed analysis and experiments in Section IV. Section V draws some conclusions.

• II.    Generalized Bernoulli shift map and Arnold

MAP

• A.    Generalized Bernoulli shift map

typically generates deterministic chaos. Such basic mechanisms are also encountered in more realistic dynamical systems. We may remark that ‘stretch and fold’ or ‘stretch, twist and fold’ provide alternative mechanisms for generating chaotic behavior. In this paper, we shall consider its generalized version shown as

x xn+1 = T(xn ) := — mod1" a

where xn, xn^ 1 e[0,1] are the states of the map, and a e (0,1) is the control parameter. As a = 0.5 , B becomes the regular Bernoulli shift map (1). A typical orbit of x derived from the dynamical system is {xk = Bk (x0), k = 0,1,- • •}, which is shown in Fig. 1(a) for a = 0.3731, x0 = 0.2709. Its waveform is quite irregular and indicates that the system is chaotic. The bifurcation diagram of the generalized Bernoulli shift map is depicted in Fig. 1(b), in which for every control parameter, we iterate 600 times to get the corresponding orbit points and plot them. It implies that the control parameters belonging to (0,1) will make the proposed system chaotic. The control parameter a and the initial condition x can be used as valid cipher keys as the map is utilized to design image encryption schemes. There exist some good dynamical features in generalized Bernoulli shift maps, such as desirable auto-correlation and cross-correlation features, see Fig. 1 (c-d) . The cross-correlation is calculated between the orbit of x0 = 0.2709 and that of yo = 0.31.

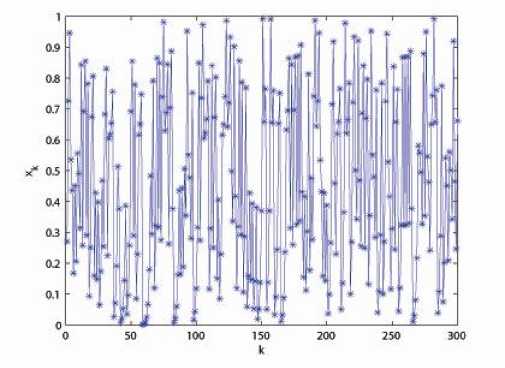
(a) A typical orbit of generalized Bernoulli shift map with a = 0 . 3731 , x ₀ = 0 . 2709 .

The Bernoulli shift map BQ : [0,1] ^ [0,1] is given by xn+1 = B0(xn ) := 2xn mod1 =

if x e [0 , 1 / 2) if x n e [1 / 2 , 1]

The Bernoulli shift map yields a simple example for an essentially nonlinear stretch-and-cut mechanism, as it

9           02          94          06          0.0           1

where the notation “ x mod 1” refers to the fractional part of a real number x by adding or subtracting an appropriate integer. Therefore ( x_n, y_n ) is confined in the unit square [0 , 1) 2 . The Arnold map is area preserving since the determinant of its linear transformation matrix is equal to 1; its Lyapunov characteristic exponents are the two eigenvalues CJ₁ and ( T ₂ of the coefficient matrix in (3), given by

^ = 1(3 + V5) >  1 , ^ = 1(3 - V5) <  1 .

(b) Bifurcation behavior of generalized Bernoulli shift map, a е (0 . 001 , 0 . 995) with step 0.005.

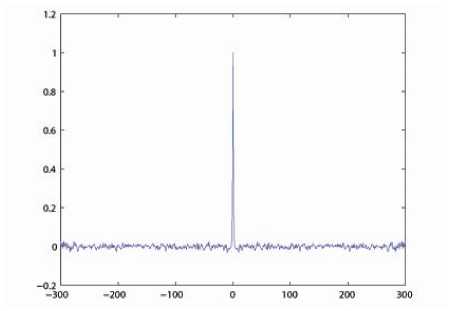
(c) The auto-correlation

It implies that the map is chaotic since one of the Lyapunov characteristic exponents is larger than 1. The two-dimensional Arnold map (3) can be extended to N -dimensional one in the following way

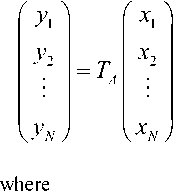
mod1

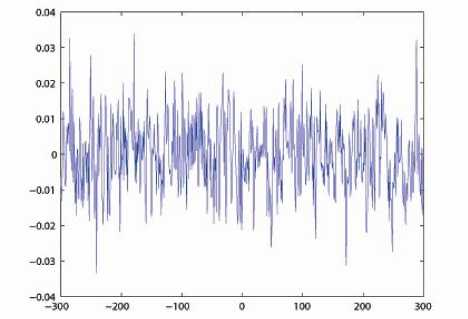
(d) The cross-correlation of two different orbits

Figure 1. Chaotic behavior of generalized Bernoulli shift map.

f 1   1    1

1  2  2

1  2  3

Ta =

1   2  3

_v 12 3

1        1

N - 1 N - 1

N -1   N

B. Arnold map

Arnold map was proposed by V. I. Arnold in the research of ergodic theory; and it is commonly known as cat face transform [23]. The map is a process of clipping and splicing that realign the pixel matrix of digital image. The classical Arnold map is an invertible map described by

The determinant of the matrix for N -dimensional Arnold map is 1, therefore the absolute values of some eigenvalues should be greater than 1 and the derived system is chaotic. In this paper, we utilize the sixdimensional Arnold map (4) and the two-dimensional Arnold map (3) to improve the sensitivity of six generalized Bernoulli shift maps in the permutation process and that of four generalized Bernoulli shift maps in the diffusion process. We will show the integration process in Section III.

(.. A x n + 1

l У п + 1 J

= Ta

( A x n

l У п J

^{1    1} ) [ xn |

11  2 Jl Уп J

mod 1     (3)

• III.    The proposed image encryption scheme

• A. Permutation process

In this subsection, we propose a permutation process to confuse plain-image totally. Assume that the processed plain-image is of width W and height H . In order to enlarge the key space and improve the sensitivity of the control parameters and initial conditions, we first generate N = 6 chaotic orbit sequences by six generalized Bernoulli shift maps and then integrate them

by the six-dimensional Arnold map to form a combined sequence. In more details, we set the initial conditions x(i, 0), i = 1, • • •, N, and iterate the generalized Bernoulli shift maps (1) to yield N chaotic orbits {(x(i,k),k = 0,1,-,i = 1,-N} of x(i,0),i = 1,-,N with given control parameters a.,i = 1,---,N . The beginning L orbit points of each orbit are deleted to avoid the transient effect, where L is a constant, for example, L = 15 in all the experiments. The truncated parts {(x (i, k), k = Lo +1,---, i = 1,---, N} are then mapped to N new orbits {(y(i, k), k = 1, • • •, i = 1, • • •, N} by the N -dimensional Arnold map (18). We rearrange all the y(i, k) values of the orbits to get one new combined orbit {(z(j), j = 1,- ••} in the manner that z ((k -1) x N + i) = y (i, k), i = 1,-, N, k = 1,2,-•  . A truncated combined orbit z(k), k = 1, • • •, 600 is depicted in Fig. 2. The truncated sequence z(k), k = 1,2, • • •, H x W is rearranged according to the order from small to large. As a result, we also get an index order number for every z(k). The index order number sequence can be applied to permute the image pixel positions and therefore can confuse the image to get a shuffled image. The permutation process is stated as follows.

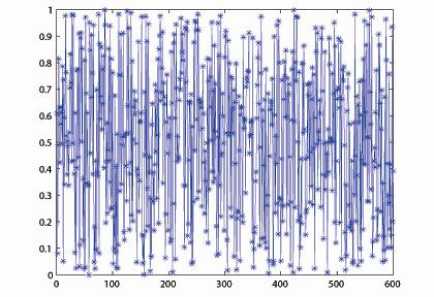
Figure 2. A combined orbit derived from six generalized Bernoulli shift maps with control parameters a = (0 . 27 , 0 . 37 , 0 . 17 , 0 . 32 , 0 . 41 , 0 . 35) and x (0) = (0 . 39 , 0 . 44 , 0 . 23 , 0 . 61 , 0 . 36 , 0 . 56) .

Step 1. Set the values of the control parameters a. , i = 1 , • • •, N and the initial conditions x ( i , 0) , i = 1 , • • •, N . Let L = ^ H ^ W J + 1 where ^ x J rounds x to the nearest integer towards minus infinity.

Step 2. Iterate the generalized Bernoulli shift map (1) x(i , k +1) = T ( x(i , k )) to get the orbit of x(i , 0) , say { x(i , k ) , k = 0 , 1 , — , L _o + L } . We choose the truncated orbits { x(i , k ) , k = L _o + 1 ,—, L + L _o} and map them to be { y(i , k ) , k = 1 , — , L } by the N -dimensional Arnold map (4)

y (1 > ^k )

y (2 , k )

y ( N , k )

= T a

f x (1 , k + L _o) )

x (2 , k + L _o)

mod1 .

( x ( N , k + L _o) J

Op[Step 3. Rearrange all the values of { y(i , k ) , k = 1 ,---, L , i = 1 ,-, N } to get one combined orbit {( z ( j ) , j = 1 , - -, N x L } given by

z ((k -1) * N+i) = y (i, k), i = 1, • • •, N, k = 1,2, • • •, L.

Step 4. Sort {z(k),k = 1,- • •,Hx W} to get one index order sequences {Iz(k), k = 1, • • •, H x W}.

Step 5. Reshape the gray-scale value matrix of the processed plain-image A sized H x W to one vector U with length H x W ; permute the vector U by Iz in the following way to get one new vector V :

V (k) = U (Iz (k)), k = 1, • • •, H x W.

Step 6. Reshape V back to one 2D matrix to yield the shuffled image B .

• B.    Diffusion process

Diffusion processes can enhance the resistance to statistical attack and differential attack greatly, in which the histogram of the cipher-image is fairly uniform and is significantly different from that of the plain-image. The opponent can not find any useful clues between the plainimage and the cipher-image and so can not break the cryptosystem even after they spend a lot of time and effort. The diffusion process is outlined as follows.

Step 1. Set L_x =^ H | W J + 1and set the values of the control parameters b. , i = 1,---,4 , the initial conditions x 1 (i , 0) , i = 1,---, 4.

Step 2. Iterate the generalized Bernoulli shift map x (i , k +1) = T ( x (i , k )) using (1) to get the orbit of x_x(i , 0) , say { x_x(i,k ) , k = 0 , 1 ,-••, L _o + L } . We choose the     truncated     parts      of     the      orbits,

{ x(i , k ) , k = L _o +1,--, L _o + L } , and map them to be { y₁ (i , k ) , k = 1< • •, L } by the two-dimensional Arnold map (3)

f y,(1, k))      f x1(1, k + Lo)

v y1(2, k) J    A (x,(2, k + L0) v

f y1(3, k))     f x1(3, k + L0)л

vy1(4,k) J    A (x1(4,k + L0)у

, k = 1,--, L , ,

, k = 1,—, L .

The two sequences y (1, k ), y (2, k ) are then piled together to form a new sequence by

TY (2 x k -1) = yx (1, k), TY (2 x k) = y (2, k), k = 1, • • •, L, while y (3, k), yx (4, k) are integrated to yield another sequence

TZ (2 x k - 1) = y (3 , k ) , TZ (2 x k ) = y (4 , k ) , k = 1,--, L .

TY , TZ are truncated to obtain two pseudo-random gray value sequences ^ ( k ) , ^ ( k ) , k = 1 , 2 ,---, H x W by

^ ( k) = P TY ( k) x 255"|, ^ (k) = fTZ (k) x 255”|, k = 1,2,-,HxW, where f x "| rounds x to the nearest integer towards infinity.

Step 3. The following diffusion function is utilized to achieve the pixel gray value diffusion

C ( k ) = ^ ( k ) © {( B ( k ) + ^ ( k ))mod 256}

Note that the inverse diffusion function is

B (k) = {^ (k) © C (k) © C (k -1) - ^ (k )}mod 256, k = 1,2,---, Hx W.

The above diffusion process implies that it can not influence the pixels before the tampered pixel with a gray value change. As a remedy, we here add a reverse diffusion process as a supplement to the above diffusion process. ^ ( k ) , k = 1 , 2 ,---, H x W are utilized to perform another round of diffusion on the sequence C ( k ) , k = H x W ,..., 2 , 1 by step 4.

Step 4. The following diffusion function is utilized to achieve more diffusion

D (k) = ^ (k) © {(C (H x W - k +1) + ^ (k ))mod 256} © D (k -1), k = 1,2,---, H x W, where D(0) can be handled as C(0) , it can be set to be part of the keys or can just take the value of ^ (1) for simplicity.

Step 5. Reshape D ( k ) , k = 1 , 2 ,---, H x W to be a matrix Q with height H and width W . Q is the resulted cipher-image.

The permutation process and the diffusion process constitute the complete image encryption scheme. The Lena image and the all-zero image are encrypted and the resulted cipher-images are shown in Fig. 3. The key parameters are a = (0.27,0.37,0.17,0.32,0.41,0.35), x (0) = (0.39,0.44,0.23,0.61,0.36,0.56), b = (0.46,0.27,0.41,0.26), x (0) = (0.3,0.23,0.43,0.83).

(a) The plain-image Lena

(b) The cipher-image of image Lena

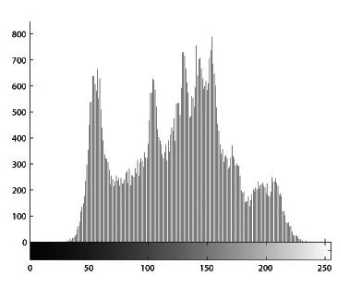
(c) Histogram of the plain-image Lena

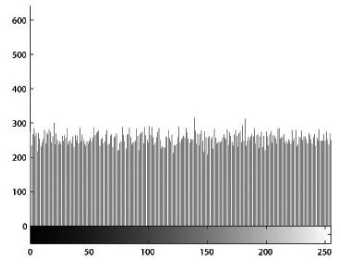
(d) Histogram of the cipher-image of Lena

(e) The plain-image all-zero

• A.    Key space and sensitivity analysis

The high sensitivity of the cipher-image to initial conditions and control parameters is inherent to any chaotic system. A good image encryption scheme needs to contain sufficiently large key space for compensating the degradation dynamics in PC. It should be sensitive to cipher keys as well, and thus can effectively prevent invaders decrypting original data even after they invest large amounts of time and resources. The analysis results regarding the sensitivity and the key space are summarized as follows. Since the permutation process is irrelevant to the diffusion process, the key space consists of the cipher keys in both processes. In the permutation process, the control parameters a , i = 1,---,N and the initial conditions x ( i , 0), i = 1, • • •, N form the cipher keys. The cipher keys in the diffusion process consist of the initial conditions x_x ( j ,0), j = 1,---,4 , the control parameters b , j = 1, • • • , 4 for the four generalized Bernoulli shift maps. The sensitivity tests with respect to all cipher keys have been carried out. The sensitivity is generally measured by means of two criteria, namely, number of pixels change rate (NPCR) and unified average changing intensity (UACI) [10,14]. They are defined as

(f) The cipher-image of image all-zero Figure 3. The encrypted results.

NPCR =   1- ^ D (i , j ) x 100 % ,

w x ht?

UACI =

|

W X H X 255 f j

C , ( i , j ) - C 2 (i , j )| X 100 %

According to the basic principle of cryptology [9], a desirable encryption scheme requires sensitivity to cipher keys, i.e., the cipher-text should have close correlation with the keys. An ideal encryption scheme should have a large key space to make brute-force attack infeasible; it should also well resist various kinds of attacks like statistical attack, differential attack, etc. In this section, some security analysis has been performed on the proposed image encryption scheme, including the most important ones like key sensitivity test, key space analysis, statistical analysis, and differential attack analysis. All the analysis shows that the proposed image encryption scheme is highly secure thanks to its high sensitivity of the control parameters and initial conditions of the generalized Bernoulli shift maps, large key space, and satisfactory permutation-diffusion architecture.

where C , C are the two cipher-images corresponding to two cipher keys with a minor change or two plain-images with only one pixel difference, D is a bipolar array with the same size as image C . D ( i , j ) is determined as: D ( i , j ) = 0 if C (i , j ) = C₂ (i , j ) , otherwise D(i , j ) = 1.

To verify the sensitivity of key parameter K , the original plain-image I = ( I(i, j))_HxW is encrypted with K = p , K = p - A K and K = p + A K respectively while keeping the other key parameters unchanged. Here A K is the perturbing value. The corresponding encrypted images are denoted by | , I ₂, I ₃ respectively. The NPCR and UACI values are calculated for the cipher-image couples ( I , I ₂) and ( I_x , I ₃) . The greater the NPCR and the UACI, the more sensitive for the parameter K . Tables I-II show the results of the sensitivity test where the initial key values are set to be the following.

Permutation process: initial conditions x (0) = (0 . 39 , 0 . 44 , 0 . 23 , 0 . 61 , 0 . 36 , 0 . 56) , control parameters

a = (0.27,0.37,0.17,0.32,0.41,0.35).

Diffusion process:

initial conditions x(0) = (0.3,0.23,0.43,0.83),

control parameters b = (0.46,0.27,0.41,0.26).

The variations AK of the considered parameters are all set to be 10-16 in the tests. We apply the proposed image encryption scheme one round with only perturbing one cipher key K with the corresponding variation value while fixing other parameters.

TABLE I.      Results regarding the sensitivity to cipher keys, part 1: calculated based on the cipher-images I , I .

K	a	a	a	a 4	a	a 6	x (1 , 0)
NPCR(%)	99.58	99.61	99.65	99.57	99.59	99.61	99.60
UACI(%)	33.36	33.43	33.53	33.47	33.63	33.46	33.41
K	x (2 , 0)	x (3 , 0)	x (4 , 0)	x (5 , 0)	x (6 , 0)	b 1	b 2
NPCR(%)	99.58	99.63	99.62	99.59	99.63	99.25	99.26
UACI(%)	33.60	33.43	33.47	33.43	33.33	33.57	33.57
K	b 3	b 4	x i (1 , 0)	x i (2 , 0)	x 1 (3 , 0)	x i (4 , 0)
NPCR(%)	99.16	99.23	99.20	99.26	99.18	99.20
UACI(%)	33.31	33.65	33.35	33.50	33.47	33.55

TABLE II.     R ESULTS REGARDING THE SENSITIVITY TO CIPHER KEYS , PART 2: CALCULATED BASED ON THE CIPHER - IMAGES | , J₃ .

K	a 1	a 1	a 3	a 4	a 5	a 6	x (1 , 0)
NPCR(%)	99.61	99.64	99.58	99.60	99.58	99.59	99.59
UACI(%)	33.40	33.38	33.57	33.48	33.15	33.54	33.52
K	x (2 , 0)	x (3 , 0)	x (4 , 0)	x (5 , 0)	x (6 , 0)	b 1	b 2
NPCR(%)	99.63	99.62	99.62	99.61	99.62	99.14	99.26
UACI(%)	33.44	33.53	33.45	33.46	33.47	33.28	33.45
K	b 3	b 4	x 1 (1 , 0)	x i (2 , 0)	x 1 (3 , 0)	x i (4 , 0)
NPCR(%)	99.16	99.17	99.16	99.29	99.07	99.14
UACI(%)	33.46	33.52	33.39	33.56	33.15	33.33

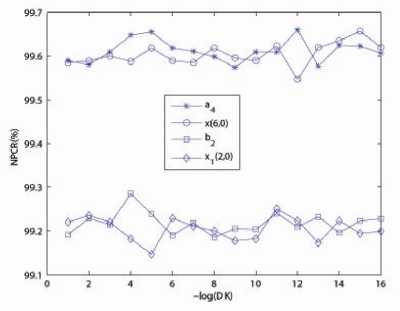
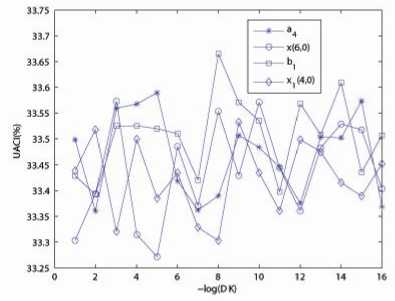
We also set the perturbing value A K from 10 ^{- 1} to 10 ^{- 16} and perform the sensitivity tests. The results are depicted in Fig. 4 which are the simulation results for a₆ , x (5 , 0) , b and x₃ (2 , 0) . The results in Tables I-II and Fig. 4 imply that all the control parameters and the initial conditions are strongly sensitive. Although the initial conditions and the control parameters for the four generalized Bernoulli shift maps in the diffusion process are less sensitive than those in the permutation process, the resulted NPCR values are all more than 99.1%.

(a)

(b)

Figure 4. NPCR and UACI between cipher-images with small changes of keys: (a) the NPCR values and (b) the UACI values.

It implies from the results that the key space is (10¹⁶ ) ²⁰ = 10³²⁰ , which is huge enough to make bruteforce attack infeasible. As a matter of fact, the key space increases as long as the number of generalized Bernoulli shift maps increases. The key space will generally become 10³² times larger if the number of generalized Bernoulli shift maps increased by 1. The sensitivity test can also be demonstrated visually, for example, see

Figs. 5-6. In Fig. 5, the image encrypted by the key a = 0 . 27 , x (3 , 0) = 0 . 23 has 99.58% of difference from the image encrypted by the key a = 0 . 27 + 10 ^{- 16} , x (3 , 0) = 0 . 23 the encrypted image with the key a = 0 . 27 , x (3 , 0) = 0 . 23 has 99.59% of difference from the encrypted image with the key a = 0 . 27 , x (3 , 0) = 0 . 23 + 10 ^{- 16} . Fig. 6 shows the encrypted image by a = 0 . 27 , x (5 , 0) = 0 . 36 , b = 0 . 41, x (4 , 0) = 0 . 83 can not be decrypted with only one of the keys a. = 0.27, x (5,0) = 0.36, b ₃ = 0.41, x (4,0) = 0.83 perturbed by a minor variation 10 ^{- 16} . For example, Fig. 6(c) shows that the image encrypted by b = 0.41 is not correctly decrypted by using the perturbed key b ₃ = 0.41 +10 ^{- 16}.

(d) Difference image between Fig. 5(c) and Fig. 3 (b) Figure 5. Key sensitive test: result I.

(a) a = 0 . 27 + 10 ^{- 16} , x (3 , 0) = 0 . 23

(b)Difference image between Fig.5 (b) and Fig.3 (b)

(c) Encrypted image with a_t = 0 . 27 , x (3 , 0) = 0 . 23 + 10 ^{- 16}

(a)plain-image Boat

(b) encrypted image with

a, = 0 . 27 , x (5 , 0) = 0 . 36 , b ₃ = 0 . 41 , x (4 , 0) = 0 . 83

(c) decrypted image with only b replaced by 0 . 41 + 10 ¹⁶

(d) decrypted image with only x - (4 , 0) replaced by 0 . 83 + 10 ¹⁶

(e) decrypted image with only a^ replaced by 0 . 27 + 10 ¹⁶

(f) decrypted image with only _x (5 , 0) replaced by 0 . 36 + 10 ¹⁶

Figure 6. Key sensitive test: result II.

• B.    Statistical analysis

Shannon pointed out in his masterpiece [35] the possibility to solve many kinds of ciphers by statistical analysis. Therefore, passing the statistical analysis on cipher-image is of crucial importance for a cryptosystem. Indeed, an ideal cryptosystem should be robust against any statistical attack. In order to prove the security of the proposed encryption scheme, the following statistical tests are performed.

• (i)    Histogram. Encrypt the image Lena with one round, and then plot the histograms of plain-image and cipherimage as shown in Figs. 3(c)-(d), respectively. Fig. 3(d) shows that the histogram of the cipher-image is fairly uniform and significantly different from the histogram of

the original image and hence it does not provide any useful information for the opponents to perform any statistical analysis attack on the encrypted image.

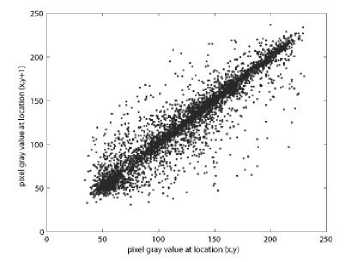
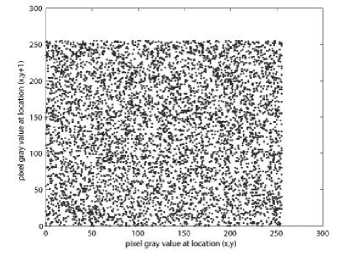
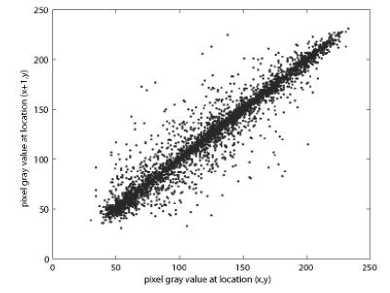
• (ii)    Correlation of adjacent pixels. To test the correlation between two adjacent pixels, the following performances are carried out. First, we select 6000 pairs of two adjacent pixels randomly from an image and then calculate the correlation coefficient of the selected pairs using the following formulae:

_(r_   ^Cov_ ( ^x,У )

V DX ) JD(y) ’

T

Cov(x, y) = T £(x - E(x))(y , - E(y)), l=1

TT

E(x) = Tzxi, D(x) = TZ(x-E(x))2, i=1                          i=1

where x , y are the gray-scale values of two adjacent pixels in the image and T is the total pairs of pixels randomly selected from the image. The correlations of two adjacent pixels in the plain-image and in the cipherimage are shown in Table III.

TABLE III.    Correlation coefficients of two adjacent pixels in two images.

	plain-image	cipher-image
Horizontal	0.9435	0.0028
Vertical	0.9680	0.0032
Diagonal	0.9157	0.0100

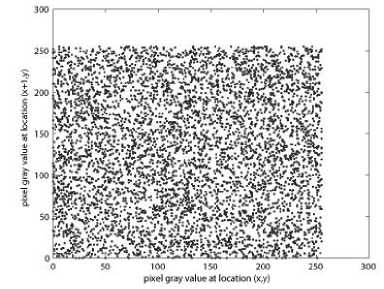
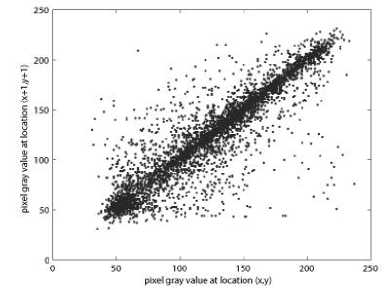
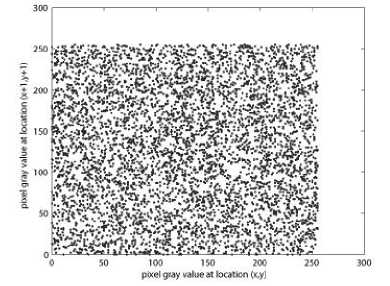
The correlation distribution of two horizontally adjacent pixels in the plain-image and that in the cipherimage are shown in Fig. 7.

(a)

(b)

(c)

• (iii)    Information entropy analysis. The entropy is the most outstanding feature of randomness. The entropy H ( m ) of a message source m can be measured by

L - 1

H (m ) = -^ p ( mi) log( p (mi)) i=0

(d)

where L is the total number of symbols m , p ( m ) represents the probability of occurrence of symbol m and log denotes the base 2 logarithm so that the entropy is expressed in bits. For a random source emitting 256 symbols, its entropy is H ( m ) = 8 bits. For the encrypted image of Lena, the corresponding entropy is 7.9969 bits. This means that the cipher-image is close to a random source and the proposed algorithm is secure against the entropy attack.

• C.    Differential attack

  

  (e)

  
  
  

  (f)

  Figure 7. Correlations of two adjacent pixels in the plain-image and in the cipher-image: (a), (c), (e) are for the plain-image; (b),(d),(f) are for the cipher-image.

  
  

In general, attackers may make a slight change (e.g., modify only one pixel) of the plain-image to find out some meaningful relationships between the plain-image and the cipher-image. If one minor change in the plainimage will cause a significant change in the cipher-image, then the encryption scheme will resist the differential attack efficiently. To test the influence of only one-pixel change in the plain-image over the whole cipher-image, two common measures NPCR and UACI, given by Eq. (5) and Eq. (6) respectively, are used. In this case, NPCR measures the percentage of different pixels numbers between the two cipher-images whose plain-images only have one-pixel difference; UACI measures the average intensity of differences between the two cipher-images. They indicate the sensitivity of the cipher-images to the minor change of plain-image. To resist difference attacks, the values of NPCR and UACI should be large enough. The test of the plain-image is Lena. We randomly select 10 pixels and change the gray values with a difference of 1, for example, we replace the gray value 66 of the pixel at position ((98,49) by 67, and get the NPCR=99.83%, UACI=41.31%. The numerical results are shown in Table IV. The mean values of the ten NPCR and UACI values are 99.77% and 38.16% respectively. We observe from Table IV that the two measure values are exceptionally good undergoing only one round of encryption.

TABLE IV.    R esults of NPCR and UACI tests of L ena .

Position	(98,49)	(235,108)	(248,14)	(41,197)	(45,34)
NPCR(%)	99.83	99.76	99.71	99.95	99.75
UACI(%)	41.43	29.36	37.63	48.40	36.60
Position	(36,255)	(178,248)	(120,220)	(102,156)	(216,36)
NPCR(%)	99.72	99.75	99.75	99.61	99.85
UACI(%)	30.01	39.42	41.32	35.16	42.42

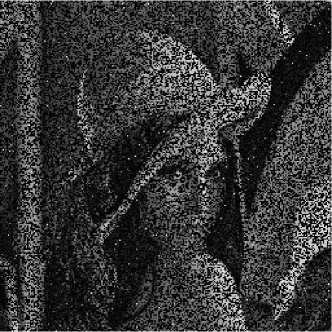
• D.    Resistance to cipher-image attacks

(d)

Figure 8. Resistance to cipher-image attacks, part I. (a), (c) are the cropped cipher-images; (b),(d) are the corresponding decrypted images from (a), (c) respectively.

(a)

(b)

(b)

(c)

(a)

(c)

(d)

Figure 9. Resistance to cipher-image attacks, part II. (a), (c)are the cipher-images attacked by salt & pepper noising (intensity 0.1) and JPEG compression (quality=80) respectively; (b), (d) are the corresponding decrypted images from (a), (c) respectively.

• V. Conclusions

An efficient image encryption scheme based on multiple generalized Bernoulli shift maps and Arnold maps is proposed in the paper. The proposed scheme can shuffle the plain-image efficiently in the permutation process. An effective two-way diffusion process is also designed to change the gray values of the whole image pixels. Security analysis including key sensitivity analysis, key space analysis, statistical attack analysis and differential attack analysis are performed numerically and visually. The robustness test of the proposed scheme against malicious attacks, like cropping, noising, JPEG compression, is also performed. All the experimental results show that the proposed encryption scheme is secure thanks to its huge key space, its high sensitivity to the cipher keys and plain-images and its strong robustness resisting malicious image processing. All the desirable properties make the proposed scheme a potential candidate for encryption of multimedia data such as images, audios and even videos.

• [1]    M. Hasler and Y. L. Maistrenko, An introduction to the synchronization of chaotic systems: Coupled skew tent map, IEEE Transactions on Circuits and Systems, 44(1997), 856-866.

• [2]    M.S. Baptista, Cryptography with chaos, Physics Letter A, 240(1998), 50–54.

• [3]    B. Schneier, Cryptography: Theory and Practice, CRC Press, Boca Raton, 1995.

• [4]    J. Fridrich, Symmetric ciphers based on twodimensional chaotic maps, International Journal of Bifurcation and Chaos, 8(1998), 1259–1284.

• [5]    L. Kocarev, Chaos-based cryptography: a brief overview, IEEE Circuits and Systems Magazine, 1(2001), 6–21.

• [6]    F. Huang, Z.-H. Guan, A modified method of a class of recently presented cryptosystems, Chaos, Solitons and Fractals, 23(2005), 1893–1899.

• [7]    G. R. Chen, Y. B. Mao, C. K. Chui, A symmetric image encryption scheme based on 3D chaotic cat maps, Chaos, Solitons & Fractals, 21(2004), 749– 761.

• [8]    R. Matthews, On the derivation of a chaotic encryption algorithm, Cryptologia, 8(1989), 29–41.

• [9]    N. K. Pareek, V. Patidar, K. K. Sud, Image encryption using chaotic logistic map, Image and Vision Computing, 24(2006), 926-934.

• [10]    G. J. Zhang, Q. Liu, A novel image encryption method based on total shuffling scheme, Optics Communications, 284(2011), 2775–2780.

• [11]    R. Ye, A novel chaos-based image encryption scheme with an efficient permutation-diffusion mechanism, Optics Communications, 284(2011), 5290–5298.

• [12]    N. Masuda, K. Aihara, Cryptosystems with discretized chaotic maps, IEEE Trans. Circuits Syst. I, 49(2002), 28–40.

• [13]    H. Liu, X. Wang, Color image encryption using spatial bit-level permutation and high-dimension chaotic system, Optics Communications, 284(2011), 3895–3903.

• [14]    S. Behnia, A. Akhshani, S. Ahadpour, H. Mahmodi, A. Akhavan, A fast chaotic encryption scheme based on piecewise nonlinear chaotic maps, Phys. Lett. A, 366(2007), 391–396.

• [15]    R. Ye, H. Huang, Application of the Chaotic Ergodicity of Standard Map in Image Encryption and Watermarking, I. J. Image, Graphics and Signal Processing, 1(2010), 19–29.

• [16]    S. Lian, J. Sun, Z. Wang, A block cipher based on a suitable use of the chaotic standard map, Chaos, Solitons and Fractals, 26 (2005), 117–129.

• [17]    V. Patidar, N. K. Pareek, K. K. Sud, A new substitution–diffusion based image cipher using chaotic standard and logistic maps, Commun. Nonlinear Sci. Numer. Simulat., 14 (2009), 3056– 3075.

• [18]    S. Li, X. Zheng, Cryptanalysis of a chaotic image encryption method, in: Proc. IEEE Int. Symposium on Circuits and Systems, vol. II, 2002, pp. 708–711.

• [19]    G. Alvarez, S. Li, Breaking an encryption scheme based on chaotic baker map, Physics Letters A, 352(2006), 78–82.

• [20]    D. Xiao, X. Liao, P. Wei, Analysis and improvement of a chaos-based image encryption algorithm, Chaos, Solitons and Fractals, 40 (2009) 2191–2199.

• [21]    J. M. Liu, Q. Qu, Cryptanalysis of a substitutiondiffusion based on cipher using chaotic standard and

  logistic map, in: Third International Symposium on Information Processing, 2010, pp.67-69.

• [22]    R. Rhouma, E. Solak, S. Belghith, Cryptanalysis of a new substitution-diffusion based     image

  cipher,Commun. Nonlinear Sci. Numer. Simulat., 15 (2010), 1887–1892.

• [23]    V. Arnold, A. Avez, Ergodic problems in classical mechanics, New York: Benjamin, 1968

• [24]    C. E. Shannon, Communication theory of secrecy system. Bell Syst. Tech. J, 28(1949), 656–715.

Ruisong Ye was born in 1968 and received the B.S. degree in Computational Mathematics in 1990 from Shanghai University of Science and Technology, Shanghai, China and the Ph. D. degree in Computational Mathematics in 1995 from Shanghai University, Shanghai, China. He is a professor at Department of Mathematics in Shantou University, Shantou, Guangdong, China since 2003. His research interest includes bifurcation theory and its numerical computation, fractal geometry and its application in computer science, chaotic dynamical system and its application in computer science, specifically the applications of fractal chaotic dynamical systems in information security, such as, digital image encryption, digital image hiding, digital image watermarking, digital image sharing.