A Secure Symmetric Image Encryption Based on Bit-wise Operation

Published Online January 2014 in MECS

In modern scenario, protection of a secret image is an important issue during transmission over internet. Due to some intrinsic features of images, such as bulk data capacity and high correlation among pixels, traditional encryption algorithm such as DES [1], Triple-DES [2], AES [3] and RSA [4] are not suitable to encrypt the digital images. Images are different from texts in many aspects such as high correlation among pixels and high redundancy. Thus, a variety of new image encryption schemes have been proposed by Wang K. et al. [5]. Although we may use the traditional encryption algorithms to encrypt images directly, but it is not a good idea for two reasons. The first is the image size is often larger than text. Consequently, the traditional encryption algorithms need longer time to directly encrypt the image data, the second, is the decrypted text must be equal to the original text, but this requirement is not necessary for image data. Due to the characteristic of human perception, a decrypted image containing small distortion is usually acceptable [8], [14, 15, 16]. According to Shujun Li. et al. [6] image encryption techniques try to convert an image to another one that is hard to understand. On the other side, image decryption retrieves the original image from the encrypted one. There are various image encryption schemes to encrypt and decrypt data, and there is no single encryption algorithm satisfies the different image types. In most of the natural images, the values of the neighboring pixels are strongly correlated. This means that the value of any given pixel can be reasonably predicted from the values of its neighbors [9, 10, 11]. Most of these algorithms are designed for a specific image format compressed or uncompressed, and some of them are even format compliant. There are methods that offer light encryption (degradation), while others offer strong form of encryption. Some of the algorithms are scalable and have different modes ranging from degradation to strong encryption [17]. Shujun Li et al. [6] have pointed out that all permutation only image ciphers were insecure against known/chosen plaintext attacks. In conclusion, they suggested that secret permutations have to be combined with other encryption techniques to design highly secured images. Mitra A et al.[7] have proposed a random combinational image encryption approach with bit, pixel and block permutations.

This paper shows a new secure encryption technique based on bit-wise XORing and shifting operations. Basically bit-wise operation is used for ciphering a block of secret bytes (size of each block is 4 bytes), after that each ciphered bytes are shuffled within N places (N is the size of secret file). Therefore our scheme is based on substitution as well as transposition, which provides additional protection of the secret data. The substitution and transposition are done using dynamic SBOX and TBOX respectively, which are made to vary for each block during ciphering. Also, the encrypted data is varied for changing single bit/byte in key (Ky) and the size of the encrypted file is same as the original secret. That shows the strong key sensitivity. The proposed image encryption algorithm is described in detail along with its security analysis such as key sensitivity analysis, statistical analysis, and differential analysis. A comparison in terms of correlation and number of pixels change rate (between the secret and encrypted images) are also done. Also the proposed scheme has been tested using different images to prove that the encryption method has a great potential and has a good ability to achieve the high confidential security.

• II.    PROPOSED SCHEME

• A.    Concept

Our proposed scheme is based on bit-wise operation and selected secret data is bmp image and the bmp image may be rgb or gray scale image. Here only bit-wise operation is used for ciphering the secret bytes (at a time 4 secret bytes are consider as a single block) and shuffled each ciphered bytes, keeping the encrypted file size same as the original secret file. Our proposed scheme satisfies block ciphering (size of block is 4) with transposition of ciphered bytes that is additionally added. Consider, our secret image (SO) file size is N. In a bmp image, number of bytes in a single row should be multiple of 4 bytes (i.e. 4 bytes alignment). Therefore total data bytes length is multiple of 4 bytes. So if we consider the size of each block is multiple of 4 bytes i.e. 4, 8, 16 etc., then no need to add extra padding bytes to make the actual size (SO) multiple of 4. Now consider the size of each block is 4 bytes and selected key (Ky) is user given variable length key (the key size is greater than or equal to 16 bytes). After that the Ky becomes fixed length digest string using hash function. For an effective hash functions, an attacker cannot find two messages that produce the same hash. The MD4[18] is a long-used hash function which is now broken; MD5[19] a strengthened variant of MD4[18], is also widely used. The U.S. National Security Agency developed the secure hash algorithm series of MD5 like hash functions: SHA-0, SHA-1 [8] etc. Although here we use MD5[19] hash function, but one can use SHA-0, 1, or 2 [20]. Now using MD5[19], the Ky becomes fixed length 16 bytes digest string (D) . So, the D is nothing but a set of 16 one byte values.

^Di = 0 to 15 ^{= { d} 0^{, d} 1^{, d} 2^{,... d} 13^{, d} 14^{, d} 15^}

If one uses another hash function then only the digest string length will be varied (i.e. 20 bytes, 32 bytes etc). Now from the 16 bytes digest string, a 32 bytes encryption key (EKy) is generated using Ky and D (II.B.3.a. function-1). This EKy is used to generate initial dynamic substitution box (SBOX) and transposition box (TBOX) using II.B.3.b.function-2 and II.B.3.c.function-3 respectively. The SBOX and TBOX are varied for each block during ciphering. Therefore, it provides an additional protection of the secret image, because only proper decryption key generates appropriate SBOX and TBOX (same as encryption phase), which are allowed to reconstruct actual secret image. The SBOX is used to cipher a block of secret bytes and TBOX is used to shuffle each ciphered bytes within N positions (N is size of the secret file). The transposition indexes are collision free using the concept of linear probing.

If the decryption key (Ky’) is different from encryption key (Ky) i.e. Ky ≠ Ky’, then secret reconstruction is not possible and it generates a completely noisy image which is impossible to guess the secret image. In this paper, our proposed scheme is used for image, although our scheme is equally applicable for any digital file (e.g. text, audio etc.).

• B.    Algorithm

The step wise encryption and decryption algorithms are discussed in following section. In the algorithms, some functions are used, which are defined in section II.B.3 and each functions are defined in form of pseudo code.

• 1)    Encryption:

Input: Secret Image (S^O) of size N and encryption key (Ky) Output: Encrypted Image (S^E) of size N

Step-1: Enter a variable length key (Ky). This key may be any crypto generated key, but here we use user given variable length key. Consider the length of key is L1, L1 ≥ 16.

Step-2: A 16 bytes digest string (D) is generated using Ky. Here we use MD5 hash function to generate 16 bytes digest string, but one can use any hash function or any random number generator.

Step-3: Now 32 bytes encryption key (EKy) is generated depending upon the Ky and D using function-1.

Step-4: Consider LT = 4. Now Substitution BOX (SBOX) is generated using function-2 and the size of the SBOX is LT×LT.

Step-5: Transposition BOX (TBOX) is generated using function-3 and the size of the TBOX is LT×LT.

Step-6: Now, calculate total number of bytes (N1) exist in secret data. Here the size of the secret file should be multiple of LT. Therefore, we have to adjust secret file size by adding some padding bytes (P, where 1 ≤ P ≤ LT-1), if N1%4 != 0. Now adjusted total number of bytes is (N) = N1 + P. Here a bmp image is considered as secret file (S^O) and the bmp file size is multiple of 4 bytes for its 4 bytes alignment of each row. So, for bmp images no need to add extra padding bytes.

Consider:

• 1.    IndexArray[N] = {0} // An array of N location and each location is initialized by zero.

• 2.    SrtB[LT] = {0} // An array of LT location and each location is initialized by zero.

Step-7: Now, LT numbers of words (W) are generated from SBOX by applying column wise XOR operation using function-4.

Example

A1	A2	A3	A4
B1	B2	B3	B4
C1	C2	C3	C4
D1	D2	D3	D4
W1	W2	W3	W4

Step-8: Select first LT number of secret bytes (S) from S^O and apply following steps to generate LT number of encrypted bytes (E) using intermediate operation such as XORing and shifting.

• 1.   For I = 0 To < LT-1

• 2.   For J = 0 To < LT

• 3.   E[J] = W[J] XOR S[J]

• 4.   End For

• 5.    For J = 0 To < LT

• 6.   If ( EvenParity(E[J]) =TRUE ) Then

• 7.   Rotate_Right (J, SBOX) //Jth row of SBOX rotate

• 8.   Else

• 9.    Rotate_Left (J, SBOX) // Jth row of SBOX rotate left.

• 10.    End If

• 11.    SBOX[2][J] = SBOX[2][J] XOR SrtB[J]

• 12.    End For

• 13.    Transpose (SBOX) i.e. SBOX[I][J] = SBOX[J][I].

• 14.    Rotate_Right (E).

• 15.    End For

  	0	1	2	3			0	1	2	3
  0	A1	A2	A3	A4	Apply line no.11	0	A1	A2	A3	A4
  1	B1	B2	B3	B4		1	B1	B2	B3	B4
  2	C1	C2	C3	C4	for row-2	2	C’1	C’2	C’3	C’4
  3	D1	D2	D3	D4		3	D1	D2	D3	D4
  		SBOX					Updated SBOX

right.

Step-9: Apply transposition of each encrypted bytes (E) using TBOX. The step wise transposition among N places is show below.

• 1.    For I = 0 To < LT

• 2.    TIndex = Transposition_Index_Generation// using function-5

• 3.   While (IndexArray[TIndex%N] != 0 )

• 4.   TIndex = TIndex + 1

• 5.   End While

• 6.  TIndex = TIndex%N

• 7.    Write E[I] in the Encrypted file (SE) in the position of TIndex.

• 8.    IndexeArray[TIndex] = 1 // 1 for not available

• 9.    SrtB[I] = S[I] // Read Secret byte will be put in SrtB array

• 10.    End For

• 11.    Swap (TBOX, SBOX) // Swap two array TBOX, SBOX

Step-10: Repeats Step-7 to Step-9 remaining (N/LT)-1 times to generate a complete encrypted file (S^E).

• 2)    Decryption:

Input: Encrypted Image (SE) of size N and decryption key (Ky)

Output: Reconstructed Secret Image (SR) of size N

Step-1: Enter the key (Ky) that is same as to the encryption key. Consider the length of key is L1.

Step-2: Generate 16 bytes digest string (D) using MD5 hash function.

Step-3: Now, Encryption Key (EKy) is generated using function-1. Also, SBOX and TBOX are generated using function-2 and function-3 respectively.

Step-4: Calculate total number of bytes (N) present in encrypted data (S^E).

Consider:

• 1.    IndexArray[N] = {0} // An array of N location and each location is initialized by zero.

• 2.    SrtB[LT] = {0} // An array of LT location and each location is initialized by zero.

Step-5: Now, LT numbers of words (W) are generated from SBOX by applying column wise XOR operation using function-4.

Step-6: Select each shuffled encrypted byte (E) from S^E, using function-5. A step wise algorithm for selecting of shuffled bytes is shown below.

• 1.    For I = 0 To

• 2.    TIndex = Transposition_Index_Generation // using function-5

• 3.   While (IndexArray[TIndex%N] != 0 )

• 4.   TIndex = TIndex + 1

• 5.   End While

• 6.  TIndex = TIndex%N

• 7.    Goto at TIndex position of encrypted file (SE) and Read E[I]

• 8.   IndexArray[TIndex]=1 //0 for available and 1 for

• 9.   End For

not available

Step-7: From step-6, LT numbers of encrypted bytes (E) are selected and the following steps are used to generate LT number of secret bytes (S).

• 1.   For I = 0 To

• 2.   For J = 0 To LT

• 3.   S[J] = W[J] XOR E[J]

• 4.   End For

• 5.  For J = 0 To

• 6.    If ( EvenParity(E[J]) =TRUE ) Then

• 7.    Rotate_Right (J, SBOX) // Jth row of SBOX rotate right.

• 8.    Rotate_Left (J, SBOX) // Jth row of SBOX rotate left.

• 9.    End If

• 10.    SBOX[2][J] = SBOX[2][J] XOR SrtB[J]

• 11.    End For

• 12.    Rotate_Right (S)

• 13.    Transpose (SBOX) i.e. SBOX[I][J] = SBOX[J][I].

• 14.    End For

• 15.    For I = 0 To

• 16.    Write S[I] in decrypted file SR.

• 17.    SrtB[I] = S[I] //put decrypted secret byte in SrtB array

• 18.    End For

• 19.    Swap (TBOX, SBOX)

Else

Step-8: Repeats Step-5 to Step-7 remaining (N/LT)-1 times to reconstruct the secret S^R.

• 3)    Control function:

In this section, we discuss some control functions, which are used in our algorithm. The control functions are shown in the form of pseudo code.

• a) Function-1: This function is used to expand the user given key (Ky). The expanded encryption key (EKy) is generated using Ky and digest string (D). The size of EKy is 32 bytes.

• ■ Encryption_Key_Generation (EKy, Ky, D) {

• 1.   P1 = 0, P2=0, P3=0

• 2.   For In = 0 To <32

• 3.   If (In%2=0) Then

• 4.   EKy[In] = D[P1++]

• 5.   Else

• 6.  EKy[In] =  (D[P2]  XOR D[++P2]) XOR

• 7.   End If

• 8.   End For

Ky[(P3++)%L1]

}

• b)    Function-2: This function is used to generate LT×LT substitution box (SBOX) using EKy. Among 32 bytes of EKy, the first 16 bytes is used to generate SBOX. But one can use any 16 bytes value of EKy to generate SBOX.

• ■    SBOX_Generation (SBOX, EKy) {

• 1.   P = 0;

• 2.   For I = 0 To

• 3.    For J = 0 To

• 4.   SBOX[I][J] = EKy[P]

• 5.   P = P + 1

• 6.   End For

• 7.   End For

}

• c)    Function-3: The following pseudo code is used to generate LTxLT transposition box (TBOX). Here we use remaining 16 bytes (another 16 bytes is used to generate SBOX) of EKy to generate TBOX.

• ■    TBOX_Generation (TBOX, EKy) {

• 1.   P = 16;

• 2.   For I = 0 To

• 3.    For J = 0 To

• 4.   TBOX[I][J] = EKy[P]

• 5.   P = P + 1

• 6.   End For

• 7.   End For

}

• d)  Function-4: This function is used to generate word

by applying column wise xoring of SBOX.

• ■    WORD_Generation (SBOX, W) {

• 1.   For I = 0 To

• 2.  For J = 0 To

• 3.  W[I] = W[I] XOR SBOX[I][J]

• 4.   End For

• 5.   End For

}

• e)    Function-5: The following pseudo code is used to transposition each ciphered bytes among N places (N is the size of secret file) using TBOX.

• ■ Transpostion_Index_Generation (TBOX, J) {

• 1.   TIndex = 0

• 2.  For I= 0 To

• 3.   TIndex = TIndex ShiftLeft I

• 4.   TIndex = TIndex OR TBOX[J][I]

• 5.   End For

• 6.   Return TIndex

}

• III.    RESULTS & DISCUSSIONS

Due to bulk data capacity, high correlation among pixels, digital image encryption is different from that of texts. But following experimental result shows strong effect of our scheme for digital images.

• A. Experimental result for rgb image

A 24 bit (453×395) bmp image is shown in Fig. 1.a as secret image. This image is encrypted using the key “hydrophobophobia” and the encrypted image is shown in the Fig.1.b. Also the following figure shows the lossless reconstructed secret image (Fig.1.c) using proper decryption key ( “ h ydrophobophobia” ) and failure of secret image reconstruction using wrong key “ H ydrophobophobia” (Fig.1.d). Underline character indicates the differing character between two keys, which is only one byte difference between two keys.

Figure 2. c.

Figure 1. 24 bit bmp image file encryption and decryption

The following graph (graph-1) shows the steep fluctuation in the indexing (transposition of ciphered bytes) caused by linear probing for two keys (single byte difference).

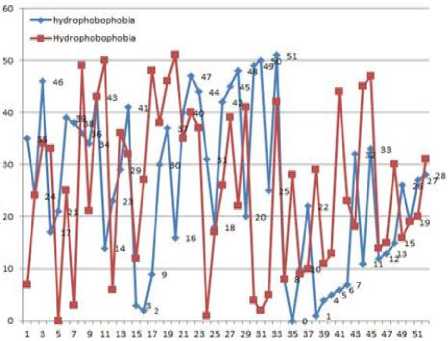
Graph-1. Transposition index of 52 bytes data for two keys (one byte difference).

Figure 2. 8-bit bmp image file encryption and decryption

The Fig.2.c shows reconstructed secret image using the key “anti-federalist s ” and Fig.2.d shows reconstructed noisy image using the wrong key “anti_federalist t ”. That has single bit difference from the original encryption key which is represented by underline (ASCII value of ‘s’, ‘t’ are 115 and 116 respectively).

Following figure shows some other experimental results for different gray scale images.

B. Experimental result for gray scale image

A (562×431) gray scale image TestImg2.bmp (Fig.2.a) is selected as secret image. This image is encrypted using the key “anti-federalists” (Fig.2.b). Fig.2.c shows the lossless reconstruction of secret image using proper decryption key and Fig.2.d shows the secret image reconstruction failure for wrong decryption key ( “anti-federalist t ” ).

Figure 3.2 (a). Img-

2.bmp

Figure 3. Different original images and encrypted images

Figure 3.3 (a). Img-

3.bmp

Figure 2. a.

• IV.    STRENGTH & SECURITY ANALYSIS

A secure encryption algorithm should be robust against all types of attacks such as cryptanalytic, statistical and brute-force attacks. Here we discuss the security analysis of the proposed algorithm by addressing key space and key sensitivity analysis, statistical analysis, and differential analysis. The resistance against different types of attack is useful measure of the performance of a cryptosystem. Therefore some security analysis results are incorporated in the following section to prove the validity of our proposed scheme.

• A.    Key Space and Key Sensitivity analysis

  A good cryptosystem should have sufficiently large key space to make the brute-force attack infeasible. Key spaces imply the total number of different keys which can be used for the purpose of encryption and decryption. The algorithm proposed in the paper uses a 16 characters, i.e. 16×8=128 bits key, so that the key space is 2¹²⁸, which is large to avoid brute-force. Also we expand the 16 bytes key to 32 bytes key, i.e. 32×8 = 256, so the key space is 2²⁵⁶, which is large enough to avoid brute-force attack according to the present computational speed. On the other hand the encryption and decryption algorithm is highly sensitive to the secret key. This scheme generates a completely different encrypted/decrypted image only for single bit/byte difference in key.

The Fig.1 and Fig.2 show that the decryption is possible only with proper key. A single bit difference key produces a completely noisy image in decryption phase. Because different key produces different SBOX and TBOX, therefore it produces different transposition index (graph-1). Following figure shows different encrypted images with single bit difference key for same secret image.

Encrypted Image

Original Image

Key:

Figure 4. Key Sensitivity

The secret image Fig.4.1 is encrypted using two keys and generates Fig.4.2 and Fig.4.3 as encrypted images. The keys have single bit difference and underline character shows the difference between two keys.

• ■   Correlation between Fig.4.1 & Fig.4.2 is [0.0016].

• ■   Correlation between Fig.4.1 & Fig.4.3 is [0.0021].

• ■    Correlation between two encrypted images (Fig.4.2 & Fig.4.3) is [0.0019].

Above correlation values show that the algorithm of the cryptosystem is highly sensitive to the secrete key and it guarantees the security against known plain-text attack. Also small changes in the key should cause a drastic change in the encrypted data. Therefore, here exists avalanche effect that is a desirable property of cryptographic algorithm.

The following graph (graph-2) shows the transposition indexes for the key “manganotantalite” and “nanganotantalite” of 52 bytes data.

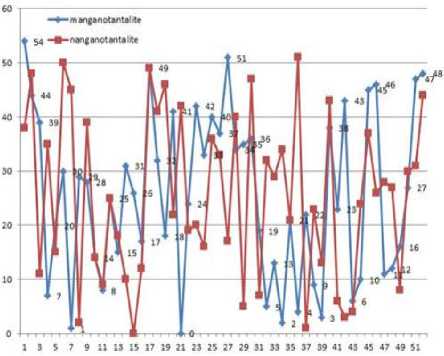
Graph-2. Transposition index of 52 bytes data for two keys (one bit difference).

• B.    Statistical Analysis

Statistical analysis is crucial importance for a cryptosystem. An ideal cryptosystem should be resistive against any statistical attack. To prove the robustness of the proposed algorithm, we have performed the following statistical test such as histogram analysis, correlation analysis, etc.

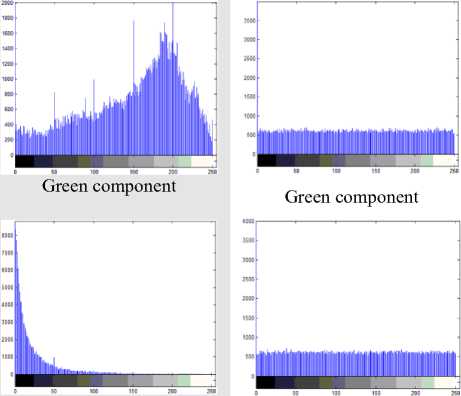
• 1)    Histogram analysis: The histogram analysis clarifies how pixels in an image are distributed by plotting the number of pixels at each intensity level. Histogram analyses on rgb and gray scale secret images with respect to encrypted images are shown in following Fig.5, 6. The histogram of encrypted image has uniform distribution which is significantly different from original image and has no statistical similarity in appearance.

  Original Image Figure 1. a

  

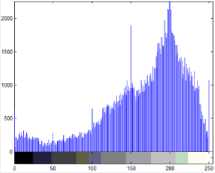
  Red component

  
  

  Encrypted Image Figure 1. b

  

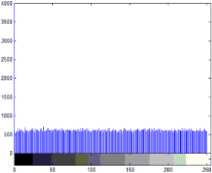
  Red component

  
  
  

  Blue component

  Blue component

  Figure 5. Histogram of rgb secret image and encrypted image

  
  

  low value of correlation coefficient shows that there is no straight relation between the original and encrypted images. Table-I shows the correlation values between different gray scale secret and encrypted images for different keys. Also, table-I shows the correlation between original secret image and reconstructed image.

  TABLE I. CORRELATION BETWEEN ORIGINAL IMAGE & ENCRYPTED IMAGE

  
  

  Input Images

  Correlation Value

  Original image Vs. Encrypted image

  Fig. 2.a & Fig. 2.b	0.00082
  Fig. 3.1(a) & Fig. 3.1(b)	-0.0013
  Fig. 3.2(a) & Fig. 3.2(b)	0.0028
  Fig. 3.3(a) & Fig. 3.3(b)	0.00086
  Original image Vs. Decrypted image
  Fig. 2.a & Fig. 2.c	1.0000

  
  

  Fig-5 shows histogram of original rgb image (Fig.1.a) and encrypted image (Fig.1.b). Histogram of ciphered image is fairly uniform for red, green and blue component and is significantly different from that of the original image.

  
  

  Original Image Figure 2. a

  

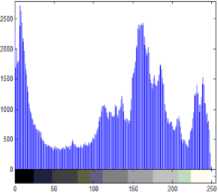
  Figure 6. Histogram of gray scale secret image and encrypted image

  
  

  Encrypted Image Figure 2. b

  
  
  

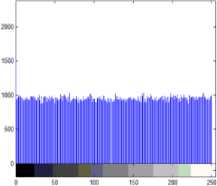
  The correlation coefficients are used to measure the similarities between the two images. The large correlation value implies the best match between the two images. Above result shows that a low correlation value exists between original and encrypted images. Therefore encrypted image is completely different from original image. Also we get the correlation value 1 between original image and decrypted image. That is the lossless reconstruction of secret image.

  3) Differential Attack: The major requirement of all the encryption techniques is the encrypted image should be greatly different from its original form. The Number of Pixel Change Rate (NPCR) is used to measure the number of pixels in difference of gray level in two images. Let C(i, j) and C’(i, j) be the ith row and jth column pixel of two images C and C’, respectively, the NPCR can be defined as

  
  

  Fig.6 shows histogram of original gray image (Fig.2.a) and encrypted image (Fig.2.b). This figure shows that the histogram of the ciphered image is fairly uniform and is significantly different from that of the original image.

  2) Correlation value: A secure encryption scheme must generate an encrypted image independent of the original secret image. Therefore, they must have a very low correlation coefficient which is very closer to zero. Here, we calculate the correlation between original and encrypted image using equation 1.

  
  

  Z, D ( i , j )

  NPCR = ^, j -----x 100

  
  

  N

  
  
  
  

  Where N is the total number of pixels in the image and D(i, j) is defined as

  
  

  D ( i , j )

  
  
  
  

  C (i , j ) = C '( i , j ) C(i , j ) ^ C '( i , j )

  
  

  ZZ ( A mn - A )( B mn - B )

  mn

  / ZZ ( A- - A ) 2 ( ZZ ( B- - B )² mn       mn

  
  
  
  

  Where A and B are mean of A and B respectively. A

  
  

  The NPCR calculates for various images using equation-2. The test results for NPCR are shown in Table-II. The high value of NPCR means the pixel values are dramatically randomized. This result indicates that the plain-image and the encrypted image are significantly different from one another, so the proposed algorithm is highly resistive against differential attack.

  
  

Input Images	Number of Pixel
Original image Vs. Encrypted image	Change Rate (NPCR)
Fig. 2.a & Fig. 2.b	99.687
Fig. 3.1(a) & Fig. 3.1(b)	99.618
Fig. 3.2(a) & Fig. 3.2(b)	99.599
Fig. 3.3(a) & Fig. 3.3(b)	99.607
Original image Vs. Decrypted image
Fig. 2.a & Fig. 2.c	0.000

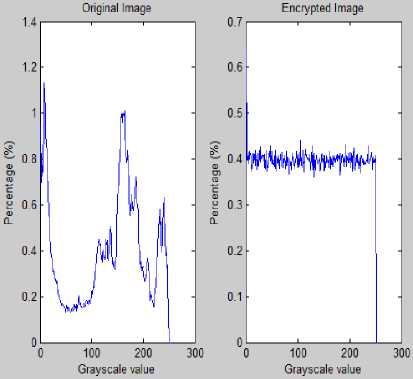
The following graph-3 shows percentage of each gray scale value of figure-3.3(a) as original and figure-3.3(b) as encrypted image.

• 4)    MSE & PSNR measure: The Mean Square Error (MSE) and Peak Signal to Noise Ratio (PSNR) for the proposed technique have been computed for different images. The high value of MSE and low value of PSNR causes the resulting encrypted image more randomness. MSE is calculated using the formula

MSE = ^Z N ZM=i[ C У, j) - C '

Where, c(I, j) and c’(I, j) be the ith row and jth column pixel of two images C and C’, respectively. M and N are number of rows and columns of original image.

PSNR can be computed by

Input Images
Original image Vs. Encrypted image	MSE	PSNR
Fig. 2.a & Fig. 2.b	129.631	25.253
Fig. 3.1(a) & Fig. 3.1(b)	105.629	27.893
Fig. 3.2(a) & Fig. 3.2(b)	200.496	25.109
Fig. 3.3(a) & Fig. 3.3(b)	166.815	29.882
Original image Vs. Decrypted image
Fig. 2.a & Fig. 2.c	0.0000	100.000

High value MSE and low value PSNR indicates that two images are completely different. On the other hand, high value of PSNR is indicates the high quality image.

• 5)    Encryption/decryption speed: For real-time application, it is very important issue to consider running speed of encryption and decryption processes. Following table shows the results of encryption/decryption speeds on 8-bit gray-scale images of different sizes. Here test is performed under the configuration of Core-i3 with 2 GB ram.

Dimension (bmp/bit depth=8)	Size	Encryption (In Sec.)	Decryption (In Sec.)
215×210	45.3 KB	1	1
562×431	238 KB	3	2
803×554	436 KB	5	3
1500×1500	2.14 MB	13	12

• V. CONCLUSION

This is a secured encryption technique for digital image; it is equally applicable for any digital file (e.g. text, image and audio etc.). The bit-wise XORing and shifting operation are used to cipher a block of secret bytes and then each ciphered bytes are shuffled within N places (N is the size of secret). This is the combination of substitution and transposition technique performed using dynamic SBOX and TBOX. The key for the proposed cryptosystem is very large which provides better security against brute-force attack. Moreover, key sensitivity analysis, statistical analysis and differential attack analysis prove the high acceptability of the proposed algorithm.

PSNR = 10 x log₁₀

R ²

MSE

Where R is 255 as gray image has been used in this experiment. Calculated results of MSE and PSNR are tabulated in the following table.

ACKNOWLEDGMENT

We are thankful to the Department of Computer Science and Engineering of MCKV Institute of Engineering, West Bengal, India and Jadavpur University, West Bengal, India for giving us the platform for planning and developing this work in the departmental laboratories.