A SEIRS Model of Tuberculosis Infection Model with Vital Dynamics, Early Treatment for Latent Patients and Treatment of Infective

Tuberculosis (TB) is an airborne disease caused by Mycobacterium tuberculosis (Mtb) bacterial [10]. It has been known since 1000 B.C., so it not a new disease. About 3 million death worldwide attributed to tuberculosis every year [4].

Since TB is a disease of respiratory transmission, optimal conditions for transmission include:

– Overcrowding

– Poor personal hygiene

– Poor public hygiene.

Most cases of TB infection are in developing countries [7]. Transmission of TB result through the tiny droplets released into air via cough and sneezes from one person to another, it’s a communicable disease. The bacteria usually attack the lungs.

In addition, according to the World Health Organization, one-third of the world’s population is infected, either latently or actively, with tuberculosis [1]. There are more cases of tuberculosis in the world today than in previous time in human [17].

Tuberculosis: Signs and Symptoms

. Cough that lasts for more than 2 weeks

. Fever

. Night sweats

• . Feeling weak & 8red

. Losing weight (without trying)

. Loss of appetite

. Chest pains

. Coughing up blood

The study of tuberculosis transmission dynamics has been of great interest to both applied mathematicians and biologists because of its universal threat to humanity [25].

A number of theoretical studies have been carried out on the mathematical modelling of tuberculosis transmission dynamics [1,5, 9,11-15,17, 18, 24, 25].

• [2]    modeled tuberculosis transmission that incorporates treatment and chemoprophylaxis. They assumed that latency infected individuals developed active tuberculosis disease as a result of endogenous re-activation, exogenous reinfection and disease relapse. Their results showed that treatment of infective is more effective in the first years of implementation as treatment results in clearing active TB immediately and there after chemoprophylaxis will do better in controlling the number of infective due to reduced progression to active TB.

The main principal aim of the current work is to improved on the SIR model of tuberculosis initially studied by [25]. TB have a long incubation period or latent at which an individuals is infected but cannot spread the infection [26,27]due to the long incubation period exposed class has been incorporated in to the model by [25].

By considering the work of authors mentioned above, we developed and analyzed a new mathematical model of tuberculosis infection to complements and extend their works by incorporating the following factors that are very important in the transmission of tuberculosis infection.

• •    Vital dynamics with unequal birth rate and death rate

• •    Temporary immunity for describing the spread of infectious disease

• •     Standard incidence rate

• •    Disease induced death due to tuberculosis

• •     Treatment of both latency and infective.

• 2. Material and Method

• 2.1 . Model Assumption

The reminder of this paper is organized as follows. In section (2), we formulate the model (3) we analysed the model to obtained the effective basic reproduction number and establishing the condition for local and global stability of the disease free equilibrium of the model and finally we discuss the results in section (4).

A mathematical model for tuberculosis infection is developed by making improvement on the previous models as actual source and can be seen from figure 1.

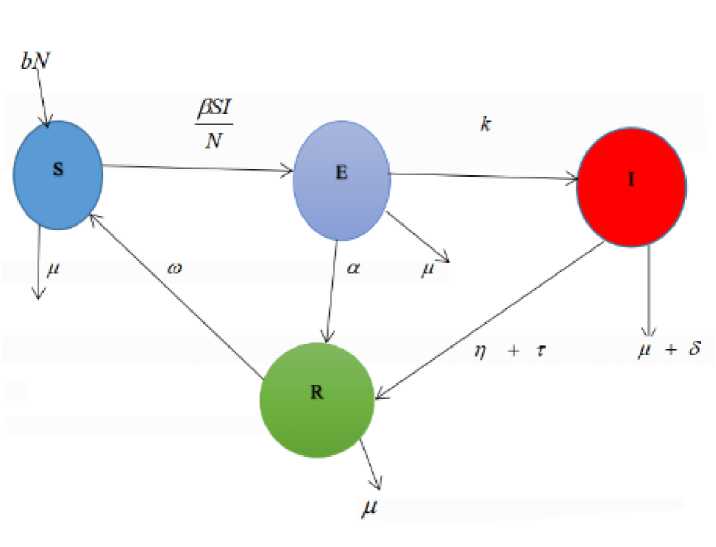
Fig. 1: Schematic diagram for Tuberculosis transmission with early treatment of latent patient and treatment of infection.

A model the spread of tuberculosis was developed with the following assumption.

• •    Homogeneous mixing, susceptible individuals acquire tuberculosis infection following contact rate with an infective individual

• •    Treatment are offered to both latency infected and infectious

• •    The infection does not confer immunity to the cure and as such the recovered components are returned back to the susceptible compartment at a given rate ( ω )

• •    The total population is compartmentalized in to four (4) epidemiological classes as shown in figure (1)

• 2.2    . Model Equation

2.3. Symbols for State Variables

The corresponding mathematical model equations are described by a system of ordinary differential equation given below:

dS ,PSI    _   _ dt       N dt N

— = (n + т)I + aE - (to + u)R dt

S E

I R

N

Number of susceptible individuals

Number of exposed individuals

Number of infected individuals

Number of recovered individuals

Total population

1.2.4.

b

u

в

Symbols for Parameters

Per capital birth rate of humans

Per capital natural death rate of humans

Transmission rate

k n

т

5 a to

Progression from E to I

Natural recovery from tuberculosis

Recovery due to treatment

Tuberculosis-induced death rate by I

Treatment rate for exposed individuals

Loss (waning) of immunity by recovered individuals.

based on biological considerations, model system (1) will be studied in the following region

which can be shown to be positively invariant with respect to the model system (1).