A Study of Half-Duplex Asymmetric Two-Way Decode-and-Forward Relaying Using Relay Selection

Published Online August 2011 in MECS

Cooperative relaying as a promising technology has attracted widespread attentions, since it can achieve higher transmission quality and throughput for wireless networks. In particular, considerable interests have focused on the half-duplex two-hop relaying, where two user terminals communicate with each other enabled by a relay node. Due to the half-duplex constraint, conventionally a direct four time-slot transmission scheme is employed for such a scenario to complete one round information exchange between the two source terminals. Although the conventional scheme is easier to implement, however, it results in a loss in spectrum efficiency due to the fact that more time slots are occupied for one round communication. In order to compensate the spectral efficiency loss, two-way relaying based on the protocols of amplify-and-forward (AF) and decode-and-forward (DF) has been proposed [1], [2]. In contrast to the conventional scheme, less transmission cycles are required in two-way relaying, which consequently provides the improvement in performance of spectral efficiency. Presently, according to the required time slots, the existing two-way AF and DF relaying can be grouped into 2-phase AF scheme, 2-phase DF and 3-phase DF schemes, respectively. Owing to occupying less transmission cycles, more benefits can be achieved from the 2-phase schemes. Thereby, relatively more attentions focus on the 2-pahse schemes in the research community.

Recently, two-way AF and DF relaying have been studied in many points of views. As an important performance measure, outage probability has been investigated for two-way communication in the literature [3]-[12]. However, in [3]-[6] the information theoretic analyses are all conducted by viewing the two-way AF relay links as two parallel one-way channels, namely separately considering outage events at the two sources. Practically, as a multi-user system, the whole network will be in outage whenever an outage occurs at any user [13]. To this end, references [7]-[10] explored the two individual outage events as a whole and derived the outage probabilities accordingly. However, their investigations concentrate only on the AF scheme with symmetric traffics. Meanwhile, papers [4], [11] and [12] conducted the outage analysis for the DF scheme. However, in [4] the two individual outage events are still separately examined. And, in [11], [12] only symmetric traffics are considered. Actually, due to various traffics that user requires in practice, the assumption that system always has symmetric traffic flows is not appropriate. Furthermore, the impact of traffic asymmetry on the outage probability of two-way relaying is still an open issue. Motivated by these facts, we conduct the information theoretic analysis of outage probability by jointly considering outage events at the two senders with asymmetric traffics. To our best knowledge, no similar studies have been reported despite the importance of such an issue.

AS well known, opportunistic relay selection is a powerful technique providing good performance for relaying protocols. Intuitively, the principle of relay selection can be further applied for two-way relaying with the aim to achieve improvement in performance. Recently, the problem of relay selection in two-way relaying scenarios has received considerable interests. In papers [5], [6], [8]-[11], several effective relay selection policies have been proposed and investigated for the AF scheme. However, only symmetric traffics are considered in these works. Recently, the authors of [14] proposed an interesting relay selection strategy for the DF scheme, where the best relay is selected according to the weighted rate sum on the boundary of the achievable rate region individually. Whereas they only investigate the DF scheme with superposition coding and outage probability is not considered. Very recently, the authors of [15]-[17] applied the max-min policy [18] for two-way DF relaying with network coding. In [15], a joint relay selection and network coding strategy was proposed and analyzed in terms of bit error rate (BER). In [16] and [17], the maxmin policy was applied in two-way multi-antenna relay networks and the corresponding performance measure of BER was analyzed. However, the asymmetry of system traffics is not an issue in their research contexts. Furthermore, Krikidis [12] researched the relay selection strategies of the max-min, max-sum and the hybrid of the two on the two-way DF relaying network and analyzed the outage probabilities accordingly. However, similar to the previous works they still focus only on the symmetric traffic. Actually, a two-way relaying network can not always operate in the symmetric traffic mode. Moreover, as [19] pointed out, traffic asymmetry has a potential impact on some performance measures of two-way relaying, such as achievable throughput and channel errors. Although opportunistic relay selection for twoway relaying scenarios has received strong interests, the impact of traffic asymmetry on the relay selection is still an open issue. Inspired by these facts, we consider a halfduplex two-way DF relaying network with asymmetric traffics (i.e., asymmetric two-way DF relaying) and study the relay selection techniques accordingly. To our best knowledge, the problem of relay selection for two-way DF relaying from the viewpoint of asymmetric traffics is not reported.

In this paper, our investigations focus on the 2-pahse half-duplex two-way DF relaying. Unlike the current research activities, we deal with the problem of relay selection and outage analysis in more general cases, including symmetric and asymmetric traffic flows, channels, and all SNR values. As a first step, the outage probability of a conventional three-node network is derived over Rayleigh fading channels. Subsequently, we consider a two-way relaying network with multi-relay nodes. For the goal of outage performance optimization, opportunistic relay selection is used. In our work, the policies of max-min and max-sum are also investigated and analyzed in terms of outage probability but from the viewpoint of asymmetric traffics. After that, new upper and lower bounds of outage probability for the two policies are presented. Moreover, the exact expression of outage probability for the max-min policy is also derived. From the analytical analysis, some meaningful insights are concluded, which are useful for the decision of relay selection policies. Finally to reduce overhead, we propose a single-criterion based relay selection policy, which uses the harmonic mean of the two-way link gains. The simulation results verify that the proposed policy is an efficient and appropriate method to implement relay selection and can achieve significant performance gains in terms of outage probability.

The rest of this paper is organized as follows. In section II, the under investigated two-way DF relaying scenario is described. In section Ш , the achievable rate region is stated and the outage probability is analyzed accordingly from the viewpoint of asymmetric traffics. In Section ^ , opportunistic relay selection is investigated for performance improvement. The conventional maxmin and max-sum policies are examined in terms of outage probability and diversity gain. Furthermore, a new relay selection policy is proposed. Numerical simulations and comparisons are presented in Section V . Section И concludes this paper.

• II.    System Model

We consider a perfectly synchronized wireless communication network with N + 2 terminals, where two source terminals want to communicate with each other enabled by one of the N relaying nodes. Suppose r and r are the information rates of sources A and B, AB , respectively. Here, we presume all the terminals have the same transmission power and are corrupted by independent additive Gaussian noise with the same variance. In particular, we assume that the two-way relaying network is able to obtain perfect channel state information (CSI) by applying training signals.

As shown in Figure 1, for DF scheme, sources A and B first send their messages to relays simultaneously during time-slot 1. Then the relay nodes receive an additive Gaussian noise corrupted superposition of the transmitted signals yR = Ph+RAR^ + PhU + wR,,i e{1-2-L-N}, (1) where the index i represents for the i - th relay node, P is the transmission power of sources A and B, sA ( sB ) denotes the unit power signal transmitted from source A(B), wR is the additive Gaussian noise at the i- th relay node with variance ст2 and h+R (hBR ) is the path gain of A ^ R ( B ^ R ). After that a best relay is opportunistically selected out of N candidates, which is used to help the information exchange between the two source terminals. Here, we assume the k - th relay node is the best one. Subsequently, the best relay jointly decode both sA and sB , followed by certain signal processing operations. Then the best relay node broadcasts the resulting signal sR to sources A and B during time-slot 2. Accordingly, source A(B) receives

Ph_R A s R + w A (    Ph_R „ s „ + w ), where P is the

Rk AR   A        Rk BR   B transmission power of the relay node, hR A (hR B ) denotes the path gain of R ^ A (R ^ B) and wA (wB) denotes the additive Gaussian noise at A(B) with variance <72. Since both sources have known their own transmitted messages, sources A and B can get their desired messages correctly through perfect decoding and a corresponding signal processing operation.

In addition, we assume that all the links are reciprocal, i.e., h = h , h„„ = h„ „ and quasi-static, namely, the ARi      RiA     BRi      RiB path gains are regarded as constant within two time slots. Without loss in generality, we assume that all the link gains are identical and independent distributed. For link A ^ R and B ^ R , let |hAR | and |hBR | be the instantaneous squared strength, which obey exponential distribution with rates 1 g1 and 1 g2 , respectively. Of note is that in this paper the unit of information rate is measured in bit/s ■ Hz .

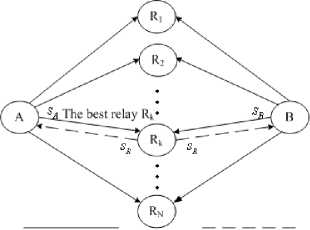
Time-slot 1                    Time-slot 2

Figure 1. Two-Way relaying system model

Ш Outage Analysis for Conventional Three-node Network

In this section, we conduct the outage analysis for a conventional three-node two-way DF relaying network. In order to simplify the notations, we first define some variables, events and cases, all of which are used in the following analyses. Let x = у \ h _RR |² , y = у \ h _RR |² , z A = ² 2 r A ^{- 1} , z B = ² 2 r B ^{- 1} , z AB = ^Z A ^Z B ⁺ z A ⁺ z B and Q = Jz_AB + 1 - 1, where у = -P - denotes SNR. According to the above assumption, we can deduce easily that x and y are independent exponentially distributed with parameters Д = 1/ y g 1 and X 2 = 1/ y g ₂ , respectively. In addition, we let

ZM = max (ZA , zB ) .

Furthermore, two complementary events are defined as

E1 = { x + y > min [ x (x + 2), y (y + 2)]} ,(3)

E2 = E1 = {x + y < min[x(x + 2), y(y + 2)]},(4)

and two useful cases are defined as

Case1: zR < — or z. < —(5)

B     1+ Z a        A 1+ z B

Case ^{2: Z}b > ^ or ^Z A

zB

1+ Z r

Of note is that, we omit the index i for the already introduced variables, since here only one relay node is involved in the system setup.

• A.    Achievable Rate Region

Since a complete information exchange for two-way relaying is composed of two time slots, the metric of achievable rate region can be calculated accordingly. According to [12], the ultimate achievable rate region of a two-way DF relaying can be given by

^Ra <  ^{min ( R} ra , ^R RB ) , ^R B <  ^{min ( R} R r , ^R rr ) , ^{for E} 1 ;

^R DF "^ ^Ra <  ^min ( ^R R uur , ^R rr ) , ^Rr <  min ( ^R uu A

Ra + Rr <  R .

R uur )

RB

for Ε₂ .

(7) where Ε₁ and Ε₂ are respectively defined in (3) and (4), [ R_a , R_B ] is the rate pair of sources A and B, and ^R A r = i^log2 ( 1 ^{+ x} ) , ^R rr = i^loS2 ( 1 ⁺ y ) ^and R _z= |log₂ ( 1 + x + y ) are the rate constrains of link A ^ R , link B ^ R and the sum-rate respectively.

• B.    Outage Analysis with Asymmetric Traffics

According to the achievable rate region, outage probability is defined as a probability that a practical rate pair [ r_A , r_B ] of a two-way relaying network locates outside the achievable rate region. To be specific, outage probability is defined as

P ou, = P { [ Ra , Rr ] ^ R DF } = 1 - P { [ Ra , Rr ] ^ R df } . (8) Further, by applying the law of total probability, (8) can be expressed as

P out, = ^{1 - P} { [ ^r A , ^r B ] e ^R DF ( ^E 1 ) , ^E 1 }

,              (9)

- P {[Га , Гв ]e R DF (E2 ) , E2 } where R DF (E1) and R DF (E2) respectively represent the achievable rate regions that event Ε1 and Ε2 occur.

From equation (9) and the above definitions, outage probability of a two-way relaying scenario can be derived accordingly.

Proposition 1: The exact expression of outage probability for a three-node two-way DF relaying network can be separately depicted by the following two cases. For the Case 1 , the outage probability can be shown as

P DF = ^{1 -} exp H ^ 1 ⁺ R2. ) z M ] , ⁽¹⁰⁾

where z_M is defined in (2).

For the Case 2 , the outage probability can be given by equation (11). And at high SNR region, the outage probability can be given by equation (12).

Proof: See Appendix A.

From Proposition 1, some interesting phenomena can be found that 1) the outage probability of twoway DF relaying is only determined by the link with greater information rate for all zB < -^^ and zA < 1^ (i.e., Case1 ), 2) the same phenomenon manifests for all -A— < z„ < z. and -B5— < z. < z„ 1+zA B A          1+zB A B

(i.e., Case 2 ) when SNR is high and channels are asymmetric, 3) while for the Case 2 , the system outage probability is determined by the sum of average two-way link strengths, the maximum information rate of the two senders and the asymmetric level of the two sources' information rates when SNR is high and channels are symmetric.

W Opportunistic Relay Selection for Multi-Relay Networks

We now consider a two-way DF relaying network with N relay nodes. Our aim, here, is to minimize the system outage probability through opportunistically choosing one relay out of N candidates, whenever system traffics and channels are symmetric or asymmetric. Our assumption here is that the two-way relaying network is able to obtain perfect channel state information (CSI) by applying training signals. Thus, with the help of such information, an opportunistic relay selection policy can be employed to guarantee the quality of information exchanges. Here, we assume the к - th relay node is the selected best relay. In addition, we reuse the k - th notation for the already introduced variables by an additional index for the relay node.

• A.    The Max-Min Policy

For the max-min policy, the best relay is chosen to maximize the minimum of the two-way channel strengths, i.e., the best relay is chosen depending on

*

m = argmax I min(|h^ |2 ,|hBR. |2), i e {1,2,l, N} . (13)

Thus according to (7) and (9), when the max-min policy is applied, the outage probability of two-way DF relaying can be written as

P DUt, - mm = ¹ - ^P { [ r A , r B ] ^{e R} D>A m ’ = ^k }

= 1 - P { [ r A , Г в ] e R DF ( E k ) , E k m * = к } .     (14)

- P { [ r A , Г в ] e R ^k_DF ( E k ) , E k m* = к }

Further by applying the probabilistic theorems, (14) can be rewritten as the following

P out - mm = ^P { z M >  min ( x k , Ук )| m* = ^k }

^{+ P} { z AB >  x k ⁺ y_k\^m * = ^k }

• ^{-    P} { z AB >  x k ⁺ Ук , ^E k|m* = ^k }                    .⁽¹⁵⁾

• ^{-    P} { z M >  min ( xk , Ук ) , z AB >  xk ⁺ y k| m* = ^k }

^{+ P} { z M >  min ( xk , Ук ) , z AB >  xk ⁺ Ук , ^E k|m* = ^k }

By observing (15), we find that the term min ( x_k , У_к )

is maximized when the max-min policy is used. However, the impact of this policy on the term xk + Ук is not very clear. In order to get useful insights into the max-min policy, two exclusive approaches (i.e., xk + Ук is independent to the max-min policy and can be maximized by the relay selection) are carried out to deal with the term xk + Ук , which consequently results in the corresponding upper and lower bounds of the outage probability. Finally, an exact outage probability expression is derived to illustrate the system outage performance, exactly.

Proposition 2: The upper bound of the outage probability for the max-min policy can be depicted by equation (16), where the variables of 1 , 1 , z. , z.„ , z „ and Q are

1    2 A AB M defined in section 3,

P 1 = ^{1 -} exp ^[- ( ^{1 +} ^ 2 ) z M ] ,                   ⁽¹⁷⁾

and the functions of Л ( d ₁, d ₂, u , v , e ) and П ( d ₁, d ₂, u , ® , e ) are defined in Appendix B.

The lower bound of outage probability for the max-min policy can be given by equation (18), where

¹ z AB exp ( ^-1 2 z AB ) , ¹ = ¹

P 2 = ¹ - exp ( ^{- 1} 1 z AB )

< 1 2 ^ - ^ ^ exp ( - ^ 2 z AB ) ^X

{ exp [ ( ^ 2 - ^ 1 ) z AB J" ¹ }

■ X ₁ ^ X ₂.

DF p out

exp ^[-1 ^ ¹^^ ] ⁺ ( z 2 B - ^zM ) ^[ ^ 1 exp ( - ^ 2 z AB ) ⁺ ^ 2 exp ( -X 1 z AB ) ] , X 1 = X 2 ;

^ ^ ₁^-¹ ^ ₇^exp ^[- ( X 1 - Я 2 ) z M - X 2 ^z ab ] ⁺ 1 2^ exp ^[ - ( ^ 2 - ^ 1 ) z M - ^ 1 z AB ] , ^ 1 * ^ 2 .

( 1 + 1 2 ) z_M , for Case1;

p

DF - up out - mm

p^DF out

”l ( ^ 1 ^{+ 1} 2 ) z M ^{+ 11} z AB ( z AB ^⁽ ^ 1 ⁺ Л :) ^zM , ^ 1 * Л ;.

- ² z m ) , 1 = 1 2 ; ]

■ ,for Case 2.

.

( 1 - P 1 ^{N -1} ) [л ( 1 , 1 2 , zab , z 2 B ,1 ) -n ( 1 , 1 2 , zab , Q ,1 ) ] ,for Case1;

= P 1 ^N

+ < ( 1 - P 1 ^{N -1} ) [л ( 1 , 1 2 , zab , z AB ,1 ) -П ( 1 , 1 2 , zab

+ P 1 ^{N -1} [л ( 1 , 1 2 , zab , z AB ,1 ) -Л ( 1 , 1 2 , zab , zm

, ^{Q ,1} ) J ,¹ ) ]

for Case 2.

( 1 - P 1N ¹ ) [л ( A , A, Zab , z f ,1 ) -n ( A , A , Zab , Q ,1 ) ] ,for Case!

DF - low p out - mm

= P l N

⁺ p N —1

x< ( 1 - P l N ^-1 ) [л ( A , A 2 , Zab , z f ,1 ) -n ( A , A , Zab

+ P 1 N ^-1 [Л ( A , A, Zab , zt ,1 ) -Л ( A , A, Zab , Zm

> for Case 2.

( 1 - P 1 ^{N -1} ) [л ( A , A 2 , Zab , z f, N ) -n ( A , A, Zab , Q , N ) ] ,for Case 1;

P DF - mm = P 1 N +^ Л ( A , A Zab , z B , N ) - P 1 N ^-1 Л ( A , A Zab , Zm , N )

- ( 1 - p 1 ^{N 1} ) n ( A , A ₂, z_ab , Q , N ) ,for Case 2.

Proposition 3: The exact expression of the outage probability for the max-min relay selection can be depicted by equation (20) at the top of this page. And at high SNR region, the outage probability for the max-min policy can be shown as

P DF - mm » P 1 N = { 1 ^- exp H ^{A +} A ) z M ] } "  •   ⁽²¹⁾

Proof: See Appendix B.

From Proposition 3, an important conclusion is revealed that the max-min policy can achieve the diversity gain N , which benefits from the system’s superior ability to explore the diversity gains. Moreover, the sum of the average two-way link strengths and the maximum information rate of the two sources determine the system outage probability simultaneously when SNR is high.

• B.    The Max-Sum Policy

For the max-sum policy, the selected best relay can provide the maximum sum of the two-way channel strengths. Specifically, the best relay is chosen according to the following criterion

_*      22

n = argmax{^1 + уг_вкД , i e {1,2, l , N }}.    (22)

Similarly when the max-sum policy is used, the outage probability of two-way DF relaying can be written as P u - ms = ¹ - ^P { [ r A , r B A ^{R k}kF\n * = ^k }

= 1 - P { [ Га , Г в ] e R DF ( E k ) , E k n* = k }

• -    P { [ Га , Г в ] e R DF ( E k ) , E k n* = k }

= ^P { z A >  min ( x k , Ук )| n* ^:

+ P{zAB > xk + yk|n* = k k}

• ^{-    P} { z AB >  x k ⁺ Ук , ^E k|n* = ^k }

• ^-    P { z A >  min ( x k , y k ) , ^Zab >  x k ⁺ УД^П* = ^k }

^{+ P} { z A >  min ( x k , Ук ) , z AB >  x k ⁺ Ук , ^E k|n* = ^k }

In contrast to the above case, here the term xk + yk can be maximized. Whereas, the corresponding impact on the term min (xk, yk) is not very clear. Similar to the former analysis, we derive the upper and lower bounds of the outage probability for the max-sum policy by separately considering the term min (xk, yk) is independent to the max-sum policy and can be maximized during the relay selection process.

Proposition 4: The upper bound of the outage probability for the max-sum policy can be shown as

0, for Case1;

DF - ^uP _         N ^-1   _e

^P out - ms    ^P 1 ^{+ P} 2

Л(^1, A zAB , A -Л( A, A2, Zab , for Case2.

(24) where p ₁ and p ₂ are given in (17) and (19), respectively. The lower bound of outage probability for the max-sum policy can also be given by (18) at the top of this page.

Form Proposition 4, we find that the max-sum and max-min policies have the same lower bound and different upper bound of the outage probability. Since the exact upper and lower bounds are more complex, it makes us difficult to decide which policy outperforms the other one directly. However, we are still able to get some insights by considering the high SNR cases. At high SNR region, the outage probability of the max-min relay selection can be bounded as

P 1 N <  P DF - ms <  P 1 , (25)

and the same measure of the max-min policy is equal to p ₁ ^N . Thereby, we can deduce that the max-min policy performs better than the max-sum policy when SNR is high. Besides, we can conclude that the max-sum policy can achieve a diversity gain between 1 and N , which is worse than the max-min policy.

• C.    The Max-Hmg Policy

Recall that [12] has proposed a hybrid scheme for relay selection for the purpose of combining the benefits from the max-min and max-sum policies, such that the performance gain can be achieved whenever SNR is low or high. Since the hybrid scheme requires a switching between the max-min and max-sum policies, thus additional overhead is needed during the selection process. Besides as [12] stated, the hybrid policy is carried out as follows: 1) the max-min policy is first applied, 2) if the switching criterion is satisfied, then relay selection process is completed, 3) otherwise, the max-sum policy is used. Thereby, the amount of overhead involved in selecting the best relay is increased significantly for the latter case, especially when the number of relay candidates is large. To reduce overhead, we propose a relay selection strategy, which uses a single selection criterion rather than switching between the two policies. As [18] pointed out, the harmonic mean of two hops link gains is a balance of the two link strengths and is a smoother version of selecting minimum one of the two. Therefore, for the goal of outage probability minimizing, we propose the following criterion

Ч - 2,г ^{1,1,l,NЙ, (26) I h^A +| hBRi\ according to which the best relay is selected. In this paper, equation (26) is termed as the max-hmg (maximum harmonic mean of the two-way link gains) relay selection policy.

Now our main task is to conduct the theoretic analysis for the proposed max-hmg policy. Unfortunately, conducting the outage analysis by deriving the exact expressions is difficult. Hence, we investigate the outage performance by Monte Carlo simulations in the next section.

V Numerical experiments

In this section, we provide some simulation results to evaluate the outage performance of two-way DF relaying as well as the investigated relay selection policies.

In order to depict the impact of traffic asymmetry on the system outage probability, we plot Figure 2. Here, we let г_л and r_B be both ranged from zero to 3bit / s ■ Hz . According to (5) and (6), we separate the rate pairs, r_A and r_B , into two categories. As shown in Figure 2, the upper left and the lower right regions represent the Case 1 , while the median region denote the Case 2 . As long as rate pairs, r_A and r_B , locate in the regions of Case 1 , only the link with greater information rate gives contribution to the system outage probability. However, as depicted in Figure 2 such metric manifests only for moderately or strong asymmetric traffic cases. When rate pairs belong to the Case 2 , the outage probability is related to the twoway links, simultaneously.

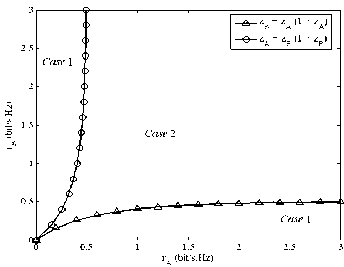
Figure 2. Separating rate pairs, r_A and r_B , into two categories, which stand for the Case 1 and Case 2 respectively

In Figure 3, two sub-figures are plotted to illustrate the outage performance of DF scenario as well as the conventional max-min and max-sum relay selection policies. Here, we let r_A be invariant and r_B be varied in a specific range. Moreover, two channel cases (i.e.

symmetric and asymmetric channels) are involved. The first observing is that the theoretical results are close to the Monte Carlo simulation results, which validate the accuracy of our derived expressions. Besides, all the cases given in Figure 3 obviously show that the max-min policy plays better than the max-sum policy for the asymmetric channels. For the high rate regime and symmetric channels, the max-sum policy can outperform the max-min policy.

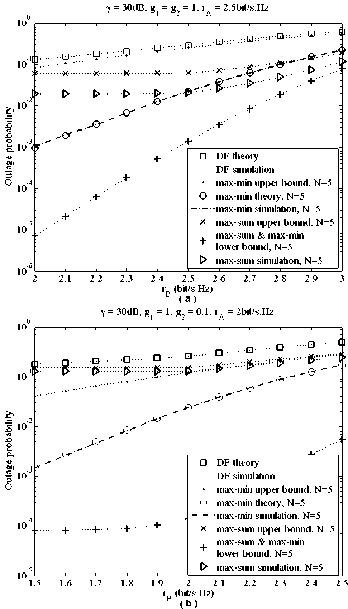
Figure 3. Outage probabilities of the conventional three-node scenario and the max-min, max-sum policies for the case where rA is invariant and rB is varied in a specific range

In the following, we make the performance comparisons in terms of outage probability among the max-min, max-sum and the proposed max-hmg policies. We first consider the case where channels are symmetric (i.e., g 1 = g2 = 1). As Figure 4, 5 and 6 illustrated, three traffic cases (i.e., symmetric, moderately asymmetric and strong asymmetric traffics) are involved in the outage performance comparisons. As shown in Figure 4 for the symmetric traffic (i.e., гл = rB = 2bit/s■ Hz) the outage performance of the max-min and max-hmg policies are inferior a bit to that of the max-sum policy in the low SNR region (i.e., SNR < 23dB ). For the high SNR regime (i.e., SNR>23dB ), the max-hmg and max-min policies perform better than the max-sum policy, and with the increment of SNR the gap between the comparing policies becomes more significant, implying that the former two are more efficient in the high SNR region. The most important observing is that the max-hmg policy always plays better than the max-min policy and achieves a diversity gain equal to N across the whole range of SNR. For the moderately asymmetric traffic (i.e., rA = 2.5bit / s ■ Hz, rB = 1.5bit / s ■ Hz ), the max-hmg can provide the best performance gains compared to the comparing policies regardless of SNR, as depicted in Figure 5. For the strong asymmetric traffic (i.e., r. = 3.5bit/s ■ Hz, r„ = 0.5bit/s ■ Hz), as can be seen AB form Figure 6, the max-hmg and the max-min perform the same and are always superior to the max-sum policy across the whole range of SNR. Additionally, we can find that the theoretic results are close to the Monte Carlo simulation results, which validate the accuracy of our derived expressions.

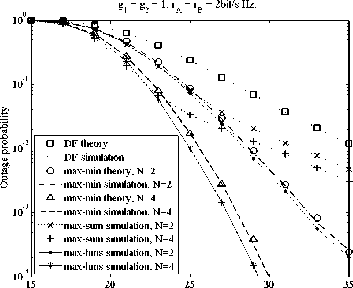
y(dB)

Figure 4. Outage performance comparison among the three examined policies under symmetric traffic and channels

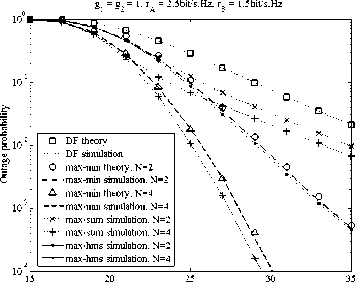
7(dB)

Figure 5. Outage performance comparison among the three examined policies under moderately asymmetric traffic while symmetric channels

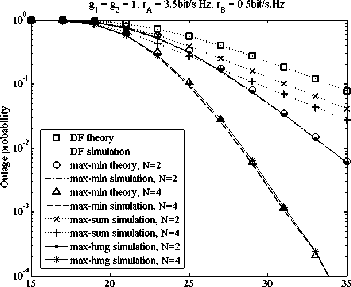
Y(dB)

Figure 6. Outage performance comparison among the three examined policies under strong asymmetric traffic while symmetric channels

For the asymmetric channels, the simulation results show the max-hmg policy is always superior to the max- min and max-sum policies across the whole range of SNR when the traffic is symmetric or moderately asymmetric. While for the strong asymmetric traffics the performance gains of the max-hmg and max-min policies are almost the same. Of note is that due to the space constraint, here, we omit the corresponding simulation results.

In general, we can conclude that the outage probability of two-way DF relaying can be measured by one-way channel for strong asymmetric traffics. For symmetric and moderately asymmetric traffics, the measure is determined by two-way links, simultaneously. Moreover, our results show that the proposed max-hmg policy can provide significant performance gains in terms of outage probability and always achieves a diversity gain equal to N across the whole range of SNR, regardless of the symmetric and asymmetric of the traffics and channels. Although, the max-hmg policy is inferior a bit to that of the max-sum policy in the low SNR region and symmetric channels, on the whole, all the results confirmed that the proposed policy is an efficient and appropriate method to implement relay selection.

И Conclusion

In this paper, we have examined the two-way DF relaying scenario in terms of outage probability from the viewpoint of asymmetric traffics and channels. Moreover, in order to make a good use of the available degrees of freedom of the channel, opportunistic relay selection (i.e., the max-min and max-sum policies) has bee studied and analyzed in terms of outage probability and diversity gain. In contrast to the current research activity that use hybrid scheme, a single-criterion based relay selection policy (i.e., max-hmg policy) has been proposed and applied in the two-way DF relaying scenario, and validated by Monte Carlo simulations. For the purpose of comparison, we have provided the exact expressions of outage probability for the max-min policy and the corresponding upper and lower bounds of outage probability for the max-sum policy. Then, numerical and Monte Carlo simulations have been conducted. Our results have shown that the proposed policy is an efficient and appropriate method to implement relay selection and can achieve significant performance gains in terms of outage probability and diversity gain. Moreover, the simulation results have validated the accuracy of our analytical analyses.

Appendix A Proof for Proposition 1

Recall that the outage probability can be expressed as

Pout. = ¹ — ^P { [ r A , r B ] ^€ R DF ( ^E 1 ) , ^E 1 } 14444244443 6

— P {[rA , rB ]e R DF (E2 ) , E2 } , 14444244443

(A1)

where Ε₁ and Ε₂ are defined in (3) and (4) respectively.

In the following, we derive the right two terms of (A1) separately. For the term 6 1 , we first rewrite it as follows

5 i = P { z_A <  min ( x , y ) , zB <  min ( x , y ) , E , }

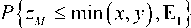
(A2)

where z_M is defined in (2). To facilitate the derivation, we calculate (A2) by separately considering the following two cases.

• (a) For x >  y , 5 1 can be written as

• ⁵ = P [ ^zm < у , x +7> ( у + 2 ) ² , x > у ^]

5 ₂ = Г² B A 2 exp ^{- A y} dy f⁽ y ^{+ 2} ) -4 A exp ^{- A}x dx ^{J z}M                   ^JzAB ^- У

+ J zAB A ₂ exp^- ^ 2 ^y dy J⁽ у ² ) ⁴ A 1 exp ^{- A} 1 ^x dx

= vA exp

zAB

.

(A8)

+^            +«

Л ₂e ^{A y}dyt       A e ^Ax dx             .    (A3)

^zm               ( y y ⁺ 2 ) - 4

= ^A 2 ^exP ( A ) J z^{+ e ex}P ^[ - ^A ( y ⁺ -2 ) ^{2 - A} У ] dy

^ 2 ( z f ^{- Z} A ) exp ( ^{- A} 1 z AB ) , A . = A 2 ;

Al^-A {exp [-^^1^^^ ]- exp [-Ai ( Zab - ZA )-^2 ZA ]} , ^1 * ^2.

(b) For x <  y , 5 1 can be written as

• ⁵ = ^P { ^zm <  ^x , у ⁺ 7 > ( ^{x +} 2 ) ² , ^x <  у }

+”           Г+Ю

= [ A e ^A dxl ₂ A ₂ e ^Ay dy            .       (A4)

J z M              ^J( x + 2 ) ^- 4

= A 1 exp (^) J exp [- A 2 ( x + . ) ² - A 1 x ] dx

Subsequently, by combing (A3) and (A4), we obtain the final expression of 5 1 ■

For the term 5 ₂, we also rewrite is as the following

5 2 = P { Za <  min ( x , y ) , Zb <  min ( x , y ) , aab <  x + У , E , }

= P { Zm <  min ( x , У ) , Zab <  x + У , E , }

(A5)

where z_AB is defined as z_AB = z_Az_B + z_A + z_B .

Also, we calculate (A5) by considering x >  y and x <  y .

• (a) For x >  y , (A5) can be expressed as

• ⁵ 2 = ^P { ^Z M <  У , z AB <  ^{x +} У , ^{x +} -4- < ( У ⁺ 2 ) ² , ^x >  У } . ^(A6) Then two additional cases should be considered, since it is significant to determine the integral region for the calculation of (A6).

• (1)    For the case where z „ <  -A— and z. < -^ B - (i.e., X A                                            B 1+ Z a              A 1+ z B X ,

Case 1 ), (A6) can be calculate as follows

5 ₂ = [ A ₂ exp ^{- A y} dy у ² ) ⁴ A 1 exp ^{- A x} dx z M                   y

= v ^exp ^[- ( A ⁺ A ) ^Zm ]               . ^(A7)

• ^{- A} 2 exp (4) J2 exp ^[ a ( y + 2 ) ^{2 - A} 2 у ] dy

• (2) For the case where z „ >  -A— and z. >  -B⁵- (i.e.,

X A                                            B 1+ Z a              A 1+ z B   X ,

Case 2 ), (A6) can be calculate as

A

Then, by combing (A7) and (A8), we obtain the final expression of (A6).

• (b) For x <  y , (A5) can be expressed as

• ⁵ 2 = P { ^zm < ^x , ^zab < ^{x +} у , у ⁺ i< ( ^{x +} 2 ) ² , ^x < у } .^(A9) As the former case, we can obtain the final expression of (A9) by calculating it in Case 1 and Case 2 separately. Then, by combing (A6) and (A9) we obtain the final expression of 5 ₂ . Finally, we can obtain the final

expressions of (10) and (11) by substituting 5 1 and 5 ₂ into (A3).

For the high SNR region, (11) can be approximate by equation (12) by using the approximation e ^{- x} « 1 - x .

x ^0

Appendix B Proof for Proposition 3

Recall that the outage probability can be expressed as

P DF. - mm = ^P { ^Z M >  min ( x k , У к )| m ‘ = ^k } ¹2 ' 6 1

^{+ P} { ^Zab > ^xk ⁺ Ук\^т* = ^k }

¹2 '

• ^{- P} { z AB >  xk ⁺ У к , ^{E k}|m‘ = ^k }                     . ^(A9)

• 1-------------------------------2

  -P{zM >min(xk,Ук),zAB >xk + yk\m* = k} 1-------------------------------------------------2

+ P { ZM > min ( xk , Ук ) , zAB > xk + Ук , Ekm‘ = k} 1-----------------------------------------------------2

For the term 6 1 , the calculation is straightforward, which is equal to p N . For the term 6 ₂, by applying the law of total probability it can be rewritten as

• ⁶ 2 = ^P { x k ⁺ У к <  z AB |mⁱⁿ ( x k , У к ) > min ( x , У , ) ,

i e N o z * к }                          , (A10)

_ P [ x k ⁺ У к < ^Zas ,^min ( x k . У к ) >^min ( x , У i ) , i e N n i # ^k ] _ 6 ₂₁

^{P [min} ( x k , У к ) >^min ( xl , У l ) , ^{z e N n i} # ^k ]            ⁶ 22

where N is defined as N □ { 1,2, l , N } . Then, we calculate (A10) accordingly. For the term 6 ₂₂ , it can be calculated as

0ц = Г ( 2 + ^)exp [ - ( 2 + Л) s ]

For the term 0 3 , we first rewrite is as follows

х [ 1 - exp( - 2 - 2 2 ) 5 ] N ^xds . (A 11)

_ у N -1 ( N -1 ) ^(-1)

= ^E l =0    t +1

Here, we used the binominal theorem

(a + в) K = E Ko [ KJ a в -1.

For the term 0 ₂₁, it can be written as follows

O21 = Г 22 e-22ydy S7 -y 21 e-2x х |^1 - exp(-2 - 22) ■ min (x, y)]N 1 dx

= £ zAB 2 2 e" ²y dy J z AB - y 2 e~^{2 1} x [ 1 - exp( - 2 - 2 2 ) ■ y ] N ^-1 dx

+ J 2 e" ²x dx J z B - x 2 2 e" ^{2 y} [ 1 - exp( - 2 - 2 2 ) ■ x ] N ^-1 dy

= ² E ГО I v ! I ^{( - 1)} ‘ Jo ² exP [ ^{- (} t ^{+ 1)( 2} 1 ^{+ 2} ■ y ] dy I N - 1 J ⁰

^- 2 2 exp I ^{2 z}a_B ) E N0 ^ N - j ^{( - 1)} t

^X J ₀ ^{2 e}xPM( ^{1 - 1)} 2 ^{+ ( 1 + 1) 2} 2 ] y } dy

+ 2 1 E N - [ N - J ( - 1) ¹ J/ exp [ - ( 1 + 1)( 2 + 2 2 ) ■ x ] dx

^- 2 exp ^(- 2 ^zab ) E Е ^ N -J ^{( - 1) 1}

х JJ AB exp { - [ ( 1 + 1) 2 + ( 1 - 1) 2 2 ] x } dx

(A12)

and further calculated as

0    0 ₃₁    P [ x k ⁺ y k < ^z AB , ^E1 ,^min ( x k , y k ) >^min ( x , y i ) , i ^e N ⁿ i * ^k J

^{3      0} 32              P _min ( x k , y k ) >min ( x, , y i ) , i e N n i * k ]          ,

(A14)

where 0 ₃₂ can be given by (A11). For the term 0 ₃₁, it can be expressed as

031 = P { xk + Ук < zAB , Ek ,min ( xk , yk )> min ( x, yi) , i e N n i * k}

= f . ' 2 . e - * ■ ' d>' JE - 4 2 1 «~ *

х { 1 - exp [ ^{- ( 2} 1 ^{+ 2} 2 ) y ] } N ¹ dy

+ [ ^W 2 e - ² 1 x dxV AB - x 2 e -²¹ y

^J 0                ^J ( x + 2 ) ² - 4 ²¹

х { 1 - exp [ - ( 2 ₁ + 2 2 ) x ] } N ¹ dy

= ² 2 ^exp ( ² ) J ₀ w { ^{1 -} exp [ ^{- ( 2} 1 ^{+ 2} 2 ⁾ у ] } N ¹

х exp _- 2 ₁ ( y + 1 ) 2 - 2 2 y J dy

• - 2 2 exp ( -2 1 Zab ) J ₀ w { 1 - exp [ - ( 2 + 2 2 ) y ] } N ¹

х exp _ ( 2 - 2 2 ) y J dy

• ^{+ 2} exp ( ^ T ) J ₀ w { ^{1 -} exp [ ^{- ( 2} 1 ^{+ 2} 2 ) ^x ] } N ¹

х exp _- 2 2 ( x + 1 ) 2 - 2 x J dx

• ^{- 2} exp ( ^{- 2} 2 Zab ) J ₀ ^W { ^{1 -} exp [ ^{- ( 2 + 2} 2 ^{) x} ] } ^{N 1}

х exp _ ( 2 2 - 2 ) x J dx

(A15) and further calculated as

N ^{- 1 (} N -^{1 ) ( 1)} ‘                                       'i- z AB -H

⁰ 21    E ₁ = 0    1 + 1    { ^{1 exp _ ( 1 + 1) ( 2 + 2 )} 2 J }

- 2 2 exp ( - 2 1 z ab ) х
^-L + y N -1 J N -1H_ x 2 +E 1 = 1 ( 1 - 1) 2 + ( 1 + 1) 2 2 х	^ з = 2 2 ;
{ 1 - exp _- ( 1 - 1) 2 Z B - ( 1 + 1) 2 2 z f ] }
N - 1 jy( -2L E 1 = 0 ( 1 - 1) 2 + ( 1 + 1) 2 2 '	, 2 * 2 2 .
{ 1 - exp _- ( 1 - 1) 2 ^2 - ( 1 + 1) 2 2 z f ] }
- 2 1 exp ( - 2 2 z ab ) х
^l + V n -1 J N zO(z2_ x 2 +E 1 = 1 ( 1 + 1) 2 + ( 1 - 1) 2 2 х	■ 2 = 2 2 ;
{ 1 - ex p [ -( 1 +1) 2 z 2 B- - ( 1 -1) 2, z f- ] }
у N -1   ( 1N -^П -                        ’ E 1 = 0 ( 1 + 1) 2 1 + ( 1 - 1) 2 2	. (A13)
	■ , 2 * 2 2 .
{ 1 - exp _- ( 1 + 1) 2 z 2 B - ( 1 - 1) 2 2 z f ] }	1

0» = 2 2 exp ( 2 ) E N -0¹ [ N - ₁ J ( - 1) ¹ exp [ х J , 2 exp { - 2 x ² - [ 1 2 + ( 1 + 1) 2 2 ] x } dx

+ 2 exp ( 2 ) E : ; 'f'   Д- 1) ¹ exp _ (^ J

J ₁ 2 exp { - 2 2 y ² - [ ( 1 + 1) 2 + 1 2 2 ] y } dy 2

^{- 2} 2 ^exp ( ^- 2 1 ^Zab )

, ^ 1 1-exp { - [ ( 1 -1) 2 1 +( 1 +1) 2 2 ] П )

^{( 1)}          ( 1 -1) 2 1 +( 1 +1) 2 2

х 5

( - 1) ¹

¹-^exp { - [ ^{( 1 -1) 2} 1 ^{+( 1 +1) 2} 2 ] n } 1,1

( 1 -1) 2 +( 1 +1) 2 2       , ² 1 * ² 2 .

Then, by substituting 0 ₂₁ and 0 ₂₂ into (A10), we obtain

the final expression of 0 ₂.

^{- 2} 1 exp ( ^{- 2} 2 ^Zab )

Q + E

N -1

1 =1

t

N - 1

( - 1) ¹

1-exp{- [ ( 1 +1) 2 1 +( 1 -1) 2 2 ] Q}       _     .

( 1 +1) 2 +( 1 -1) 2 2       , ^ 1 = ²

х5

( - 1) ¹

1-exp{- [ ( 1 +1) 2 1 + ( 1 -1) 2 2 ] Q} .       .

( 1 +1) 2 1 +( 1 -1) 2 2       , ² 1 * ² 2 .

(A16)

Then, by substituting 0;l and 032 into (A14), we obtain the final expression of 03.

For the term 0 ₄, we rewrite it as

0 _ 0 ₄₁ _ P [min ( x k , У к ) < z M , x k ⁺ У к <  z AB >( x k , У к ) >^miⁿ ( x , y t i e N ⁿi# к ^]

• ^{4      0} 42                     P ^[min ( x k , У к ) >mm ( x i ,y , ) , i e N n i # к ^{]                 .}

(A17)

Here, the term 0 ₄₂ can be given by (A11). For the term 0 ₄₁, two additional cases, i.e. Case1 and Case 2 should be considered when determine the integral region for the calculation.

• (a)    For the Case1 , we have 2 z_M >  z_AB . So, the integral region is the same as that of 0 ₂₁ . Therefore, 0 ₄₁ can also be given by (A13). So, we have 0 ₄ _ 0 2 .

• (b)    Compared to the Case 1 , the integral region is reduced for the Case 2 . Then, the final result of 0 ₄₁ should be subtracted 5 N from 0 ₂₁, where 5 N can be written as

zAB

5N _ f 2 "2e""2ydyf лв 21 e""1 x [1 - exp(-" - "2)y]   dx zM              y

+ J J AB 2 1e-"x dx J z AB - x 2 2e~" ^y [ 1 - exp( - 2 1 - 2 2 )x ] N -1 dy

_ 2 2 JJ AB e" " ^y ( e" " ^y - e" " ^z AB e " ^y ) [ 1 - exp( - 2 1 - 2 2 ) y ] N -1 dy

+ 2 1 JJ AB e" " ^x ( e" ^{2 x} - e" ^{2 z} A^B e " 2 ^x ) [ 1 - exp( - 2 1 - 2 2 ) x ] N -1 dx

(A18)

and further calculated as (A19). Thereby, 0 ₄₁ can be given by (A20), and 0 ₄ can be given by 0 ₄ _ ^{0 21}-ⁱ . For

• ^{5      0} 52                       P [min ( x k , y_k ) >min ( x , y ) , i e N n i # к ]                   ^.

(A21)

As the former case, 0 52 can also be given by (A11). For the term 0 51 , the integral region is the same as that of 0 31 due to z 2. + 2 z „ >  z.„ . So, we have 0,. _ 0 . and further

M MAB            51  31

obtain 0 5 _ 0 ₂. Consequently by substituting 0 , 0 ₂, 0 ₃, 0 4 and 0 5 into (A9) we obtain the final expression of (20) in the main part of this paper.

Moreover, in order to simplify the notation, we define two functions Л ( d 1 , d ₂, u , v , e ) and П ( d 1 , d ₂, u , o , e ) . The former is given as

Л(d 1, d2, u, v, e)_ф("DJ2eu’v,e),(A22)

where Ф ( d 1 , d ₂, u , v , e ) is given by equation (A23) and

Jt 2-1 ) '

D (e )_£ t-1

And the latter is depicted as

П(d 1, d2, u, to, e)_T(d1Dd2e7,e) ,(A25)

where T ( d 1 , d ₂, u , o ,e ) is given by equation (A26) and D ( e ) is given in (A24). According to the above analyses, we have the results given by (A27). Consequently, by using the approximation e - ^x ® 1 - x , we can obtain x ^0

equation (26) in the main part of this paper.

the last term 0 5 , we rewrite it as

5N _E N-1 (N -1+1) {exp Ht+1) (21+"2) zm ]-exp [-(t+1) (21+ "2) z2r ]} zAB

" 2 ( 2 ^Z M

) exp ^(- " 1 z AB ) + " 2 exp ^(- " 1 z AB ) ^ N ^-1 ( ₇^ ₇ + _K

^-< x { ^exp [ ^{- (} t ^- 1) 2 1 ^z M ^{- (} t ⁺ 1) 2 2 ^z M ] ^{- e}xp ^{[- (} t ^- 1) 2 1 ^f ^{- (} t ⁺ 1) 2 2 ^f ] } , " 1 ^_ " 2

" 2 exp ( ^- " 1 z AB ) ^ N -¹ ( t - N 2 + ₍ t + )) 2 2 ^x { exp [ ^{- (} t ^{- 1) 2} 1 z

- ( t + 1) 2 2 zm ] - exp [- ( t - 1) " 1 ^z^ - ( t + 1) 2 2 ^z^ ] } , 2 1 # " 2 .

1 I zm       i           1           1 к 1 W N -1 ( N -1⁾⁽ 1) t

" 1 ( "f - z M ) exp ^{(- 2} 2 z AB ) ⁺ " 1 exp ^{(- 2} 2 z AB ) L t _1 ( t + 1) " , + ( t - 1) " 2

- ^X { exp [ ^{- (} t ^{+ 1) 2} 1 z M - ⁽ t - ^{1) 2} 2 z M ] - exp ^{[- (} t ^{+ 1) 2} 1 z 2T - ⁽ t ^{- 1) 2} 2 ^f ] } , " 1 ^{_ 2} 2 ;

" 1 exp ( ^{- 2} 2 ^zab ) ^ N ^-1 ( t + 1 N " - ¹ ' ⁽ t - ) 2 2 { exp [ ^{- (} t ^{+ 1) 2} 1 z M

- ( t - 1) 2 2 zm ] - exp [- ( t + 1) 2 1 zf - ( t - 1) " 2 zt ] } , " 1 # " 2 .

(A19)

t. V-n )

0 = 0 - 5 " = S "- (-"-^ { 1 - exp [- ( t + 1 ) ( 2 1 + ^ 2 ) z ] }

- 22exP (-A zAB )X

z M ⁺ S t =1 ( t -1) 2 , + ( t +1) 2 2 ^{{ 1} exp ^{[ (} t ^{1) 2} 1 z M ⁽ t ⁺ 1) ^ 2 z M ^]} , A = ² 2 ;

S ( t ^N V( t + )) 2 2 { 1 — exP [ ^{- (} t "  ^{1) 2 Z} M — ⁽ t ^{+ 1) 2 Z} M ] } , ² * ²

(A20)

^- 2 1 exp ( - 2 2 ^Zab ) ^X

N -1 I N —1 | (-1) '

z M ⁺ S t =1 ( t +1) 2 +( t -1) 2 2 ^{{ 1} - ^{exp [- (} t ^{+ 1) 2} z M - ⁽ t - ^{1) 2} 2 z M ^{]} 2} 1 = ² ;

S    t +⁽ 1 " V( t ¹) 2 2 { 1 - exP [ ^{- (} t ^{+ 1) 2} z M - ⁽ t - ^{1) 2} z M ] } , ² * ²

e -1 I t J(-1) t

^ф ( d 1 , d 2 , u , v , 6 ) = S _t =0 " t + 1 { 1 ^- exP [ ^- ( t ⁺ 1 ) ⁽ d 1 ⁺ d 2 ) v J }

- d ₂ exp ( - d 1 u ) x

v ⁺ S e t - 1 e -‘t+ 1) d 2 { 1 ^- exp ^[ ( t ^- 1) ^d 1 v ^{- (} t ⁺ 1) ^d 2 v ] } ^{, d} 1 = ^d 2 ; S e =0 ( t - 1 e A + 1) d 2 { 1 ^- exp [ ( t - 1) d 1 v ^{- (} t ⁺ 1) d 2 v ] } , d 1 * d 2 .

(A23)

- d 1 exp ( - d 2 u ) x

e-1 (t ,)(-1)t v+St=1 (t+1 ed,+(t-в d2 {1- exp [-(t+1)2 v- (t-1)2 v ]}, d 1 = d 2;

S e =0 ( t + 1 ed 1 + (( t - 1) d 2 { 1 ^- exP ^{[- (} t ⁺ 1) ^d 1 v ^{- (} t ^- 1) ^d 2 v ^] } , d 1 * d 2 .

e -1 d t                                   W+ +¹

^ ( d , d ₂, u , ® , e ) = d ₂ exp^)^2          ( - 1) exp [ ¹ ₂ ² ]J[ ² exp{- d_xx ² - [ 2 + ( t + 1) ^di ] x}dx

^{12            2} 4xM^t- 0 _{( e} - ¹            _L 2 jj 2          ^{1       1}         2i

d t    ^                         w+ +1

+ d 1 exp ( -42- ) S _t = ₀ 1      J ^{( - 1)} t ^exP [ (⁺ )2^{1+ 2} ] ( 1 ² exp { - d 2 y ^- [ ⁽ t ⁺ 1) d 1 ^{+ td} 1 ] y } dy

V ^{e 1}7                         2

d ₂ exp ( - d 1 u )

x 5

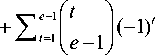
1-exp { - [ ( t -1) d , +( t +1) d 2 ] rn ) ( t -1) d , + ( t +1) d 2

, d 1 = d ₂;

d ₂ exp ( - d ₂ u )

x 5

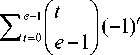
1-exp { - [ ( t -1) d , +( t +1) d 2 ] ® }    7       7

( t -1) d ₁ +( t +1) d 2        , d 1 * d 2 .

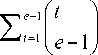
1-exp { - [ ( t +1) d 1 +( t -1) d 2 ] ^ } ⁽ t ⁺¹⁾ d 1 ⁺⁽ t ^-1) d 2

( - 1) t , d 1 = d ₂;

(A26)

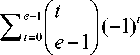
1-exp { - [ ( t +1) d , +( t -1) d 2 ] ® }    7        7

( t +1) d , +( t -1) d ₂        . d 1 * d 2 ^.

0 2 = P { z AB >  x k ⁺ Ук\^т * = ^k } = ^Л ( ² 1 , ² 2 , z AB , z 2T , " ) ;

6 3 = ^P { z AB >  xk ⁺ У к , ^{E k}|^m * = ^k } = ^П ( ² 1 , ² 2 , z AB , ^Q , " ) ;

⁵_f                                      I .      1    |^л ( 2 1 , 2 2 , ^z AB , z 2 B -, " ) ^,for Case¹;           ^(A27)

⁶ 4 = P { z M >  min ( x k , У к ) , z AB >  x k ⁺ У к m = ^k } =5

[л ( 2 1 , 2 2 , z_AB , z_A , N ) , for Case 2.

• ⁶ 5 = P { z M >  min ( x k , Ук ) , z AB >  x k ⁺ Ук , ^{E k} m * = ^k } = ^П ( ² 1 , ² 2 , z AB , ^Q , ^N )

Acknowledgment

This work is supported in part by the National Natural Science Foundation of China (Grant Nos. 60972039, 60872002, 61071086, 61001077 and 61071093) and the Scientific Research Foundation of Nanjing University of Posts and Telecommunications (Grant No. NY210072).