A Study of Hyperelliptic Curves in Cryptography

Published Online August 2016 in MECS DOI: 10.5815/ijcnis.2016.08.08

Hyper elliptic curves are being used in many important research fields like pseudo random numbers generators [21], coding theory [4, 10, 20], number theory algorithms [1, 18, 19] and cryptography [22, 23, 24, 25, 26] .

In 1989, Koblitz suggested using hyper elliptic curves instead of elliptic curves in order to design cryptography systems based on discrete logarithm problem (DLP). Hyperelliptic curves are expanded forms of elliptic curves. In other words, an elliptic curve is a hyperelliptic curve of genus 1. Having a short key size is the main advantage of hyper elliptic curves. It means that a hyper elliptic curve needs a smaller finite field to reach some level of security compared with an elliptic curve.

Further, group order of a hyperelliptic curve of genus g on a finite field with q element(s) is q ^g . So, in order to make a group of the order 2 ¹⁶⁰ by using an elliptic curve, one needs a finite field with 2 ¹⁶⁰ elements. Whereas to make the same group using hyperelliptic curves of genus 2, only one finite field with 2 ⁸⁰ elements will be needed. Likewise, for hyper elliptic curves of genus 3 and 4 a finite field with respectively 2 ⁵³ and 2 ⁵¹ elements will be required [25].

Of course, regarding researches done on hyper elliptic curves of genus 4, 5, 6, … these curves have a lower security level [14]. Contrary to elliptic curves which do not allow using index calculus algorithm for solving discrete logarithm problem, on hyperelliptic curves this attack is possible; which is considered a major shortcoming for them. Regarding the complexity of computations on hyperelliptic curves, it is very important to find appropriate hyperelliptic curves and improving their computations in order to make cryptography systems based on these curves applicable. Today, hyperelliptic curves of genus 2 and 3 can be efficiently obtained so that the resulted group will have an almost prime order.

Table 1. List of Abbreviations.

Wireless Sensor Networks	WSN
Elliptic Curve Cryptography	ECC
Hyperelliptic Curve Cryptography	HECC
Genus of hyperelliptic curve	g
considered the nth expansion of F q	F qn
Jacobin of a hyperelliptic curve C defined on F n .	J ( Fq n )
Multiplicative group of F *	F q * n
Multiplication/Inverse	1 M ]
Pairing function	П т

• II.    Mathematical Preliminaries

Some mathematical preliminaries are explicated below.

Definition 1: Suppose K is a closure of the field K. A hyper elliptic curve of genus g (g > 1) on K is C:y2 + h(x)y = f (x)gK[x,y]   (1). So that, h(x)EK[x] is a polynomial of the maximum degree g, and f (x )e K [x ] is a singular polynomial of degree 2g +1 , and this equation and its partial differential equations that are 2y + h (x ) = о and h ‘(x )y -f'(x ) = о don’t have a common solution on K . We call (x, y )e K x K a singular point on curve C if it is answer to the three above equations at the same time.

Definition 2: Suppose L is an expanded field of the K field. The set C(L) includes all L-rational points on C. It is consisted of points P =(u ,v )e L x L so that they hold true in relation(1) with a point in infinity that is shown by да. The set C (K ) is briefly called C.

Example 3: A genus 2-hyperelliptic curve and h ( x ) = о on real numbers’ field is introduced.

C : y ² = x ⁵ - 5 x ³ + 4 x

-10

-20

-30

-4         -3         -2          -1          0          1          2          3          4

Fig.1. Hyperelliptic curve C on R giant- step, Pollard and Pohlig-Hellman algorithms. Running time for the first and the second algorithms is radical of the group size and running time for the third algorithm is square root of the largest prime factor of the group order. Because in cryptography applications the group’s order is prime or almost prime, so, all these algorithms have square root time. The first index calculus algorithm to solve discrete logarithm problem on the Jacobin of a hyperelliptic curve was introduced in [2]. Also, the guidance account attack offered in [14] was the first instance of a public attack to the discrete logarithm problem defined on the Jacobin of low-genus hyperelliptic curves which had a shorter running time than the group order’s square root. These definitions and theorems are needed.

Definition 7: Suppose D and D are two elements of J_q So that D ₂ e< D_x >. The discrete logarithm problem on the Jacobin of a hyperelliptic curve for the pair ( D_x , D ₂) is computing the smallest number ЛеN so

Definition 4: Suppose P = ( x , y ) is a finite point on curve C. The opposite point of P is P = ( x , - y - h ( x ) ) so that P is on C . Also, the opposite point of ^да is considered да ( да = да ) . If a finite field P holds true in P = P , it is called a special point.

Example 5: Suppose curve

C : y ² + xy = x ⁵ + 5 x ⁴ + 6 x ² + x + 3 is defined on finite field Z₇ . Thus, g = 2, f ( x ) = x ⁵ + 5 x ⁴ + 6 x ² + x + 3 and h ( x ) = x . It is obvious that C does not have a singular point, So, C is a hyper elliptic curve:

Point (64 و ) is a special point.

Here is a method of computing number of group members resulted from a hyperelliptic curve. Consider J the Jacobin of a hyperelliptic curve C defined on F . Also, F is considered the nth expansion of F and N is order of the abelian group (J (Fn)).

that D₂ = ЛD_X .

Theorem 8: Take C as a hyper elliptic curve of genus g on the finite field Fq . If lnq < (2g + 1)' ^ then c < 2.181 exists so that the discrete logarithm problem in Jc (Fq), in the time duration L^2g +1I —,c I is computable [2].

Theorem 9: Take C as a hyperelliptic curve of genus g , defined on the finite field F_q . If q >  g ! then the discrete logarithm problem in J_c ( F_q ) in the time duration

O ( g q 2 ^+G ) is computable [14].

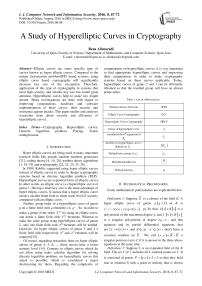
Of course, many improvements of the index calculus algorithm on hyper elliptic curves have been offered some of them have results as follows.

Take size of factor base as P |= O ( g ²q ^{( g} / ^{( g + 1 )) + f} ) and C as a hyperelliptic curve of genus g on the finite field F_q . If q >  g ! then the discrete logarithm problem in

J_c ( F_q ) in the time duration O

(   2-—+. I g 5q g+1

is solvable.

Result 6: Suppose C is a hyper elliptic curve of genus g

defined on F q ⁿ

and N_n =| J ( Fn )| . Then this relation

Now, if the factor base size is O

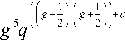
then

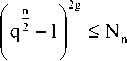
_n        2g

< I q 2 + 1 I holds and thus N_n « q^ng .

this time is _O I _g 5 _q ²"2 g + 1^{+ £} ) [33]. If | P B | = O ( g²q^{( ( g} 1)/ ^{g ) + £} )

then this time is o I _g⁵_q² g^+£ I [16].

• III.    Attacks

There are some attacks aimed at hyperelliptic curves. 10 years after Koblitz introduced hyperelliptic curves to cryptography (Diffie-Hellman key exchange) the best attacks of discrete logarithm problem for these curves were square root algorithms. Square roots algorithms are public key algorithms used for solving discrete logarithm problem in every group including shank’s baby- step

Theorem 10: For —g—— >  t discrete logarithm Ln ( q )

problem in Jc (Fq) , there is a hyper elliptic curve of genus g on F with maximum complexity of

L _q g

1P2

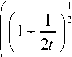
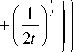
[11, 12].

As mentioned before, there is an index calculus attack with complexity O g5q g I and for g=3, 4 security level decreases.

For a genus 4-hyperelliptic curve defined on F , the discrete logarithm problem in J_c ( F ) with the

0.375        (  !+=j complexity O I Jc (F)    ) = O I q2 I will be solved.

So, the discrete logarithm problem of this case is weaker than the one generally mentioned. For g=3, this complexity is O

0.44         (   ⁴ +E j

(I ^J C ( F . J ) = ^O ( q ³ A .

It shows that almost all genus 3-hyper elliptic curves are weaker than the elliptic curves. Therefore, it is possible to say that for hyper elliptic curves of genus g >  4 index calculus attack can be done.

As a result, they are not appropriate to be used in public key cryptography. In case of using them, the group size must be well increased. Also, among hyper elliptic curves of other genus i.e. g = 1,2,3 , for g=3 , the group size must be selected in a way to prevent index calculus attacks offered in [33].

One other current attack for hyperelliptic curves is the descent Weil attack. This attack happens either if there is a composite finite field i.e. F so that, m is composite, or if m is a prime number that for a small number t holds true in ( 2 t = 1 mod m ) . Therefore, m must not be Mersen’s or Fermat’s prim number.

However, in such a case, using GHS algorithms and their improvements [15], the discrete logarithm problem can be solved. So, to prevent this attack, the curve must either be defined on a prime finite field F or a finite field F in which m is a prime number and order of number 2 in the multiplication group of p mode is a large number i.e. in relation 2 t = 1 mod p , t is a large number.

• •    Scalar multiplication of HECC with g=3 and h(x)=1 is always faster than that of HECC with g=2 .

• •    Scalar multiplication of HECC with g=3 is most often faster than ECC with affine coordinates.

• •    With an identical security level, software implementations of HECC with g=2 and g=3 ECC are equally efficient whereas hardware implementations of HECC with g=2 and g=3 are more efficient than that of ECC.

  •

  
  

  •

  
  

Scalar multiplication of HECC with g=2 and g=3 and

ECC with affine coordinates are equal if

I — I (Multiplication/Inverse) is small. In case this relation is big, then HECC with g=2 and g=3 is more efficient than ECC with affine coordinates.

If the relation(— 1 is small, HECC of genus g=2 is quite efficient and if (—j is big, HECC of genus g=3 is more efficient.

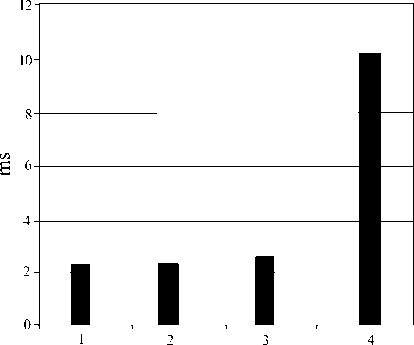
genus

Fig.2. Comparing Scalar Multiplications on Pentium 4 @ 1.8GHZ for 2 ¹⁶³ Security Level [34]

Table 2. Comparing of Key Size in HECC[33]

Security level	Elliptic Curve	Genus 2 Curve	Genus 3 Curve
256	94	47	32
512	128	64	43
1024	174	87	58
2048	234	117	78
4096	313	157	105
8192	417	209	139
16384	554	277	185

• IV. Comparing HECC and ECC

The followings are some conclusions regarding the comparison between HECC and ECC:

• • ECC with projective coordinates is almost always the most efficient system.

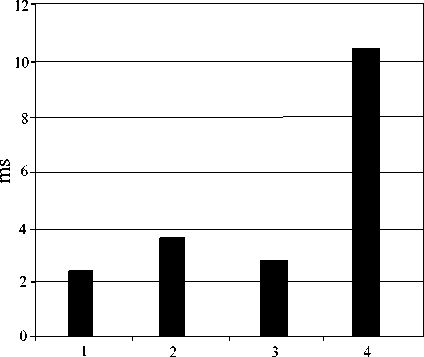
genus

Fig.3. Comparing Scalar Multiplications on Pentium 4 @ 1.8GHZ for 2 ¹⁸⁰ Security Level [34]

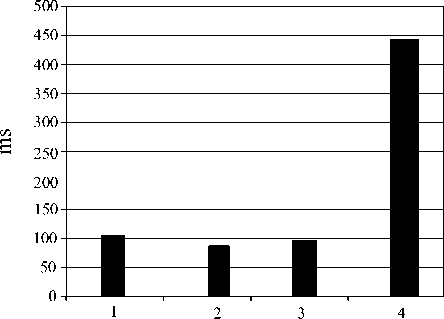
genus

Fig.4. Comparing Scalar Multiplications on ARM 7 TDMI @ 80MHZ for 2 ¹⁶³ Security Level [34]

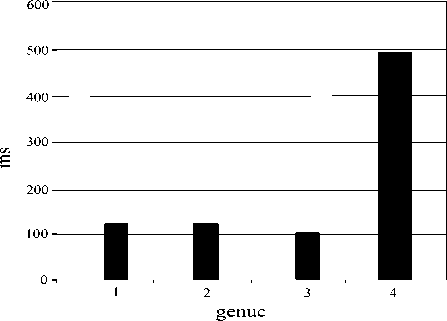
Fig.5. Comparing Scalar Multiplications on ARM 7 TDMI @ 80MHZ for 2 ¹⁸⁰ Security Level [34]

As it is clear, in hardware implementation for a security level of 2¹⁶⁰ , the genus 2-hyperelliptic curves are more efficient than hyper elliptic curves of genus 3 ; whereas with a security level of 2¹⁸⁰ it is the other way round [35].

Before this, it was generally agreed that because computations of genus 4-hyperelliptic curves were much more costly than hyper elliptic curves of smaller genus, hyper elliptic curves were not appropriate for application. While new findings show that for applications with lower security levels, genus 4-hyperelliptic curves are faster than genus 2-hyperelliptic curves. Moreover, it not only is as efficient as hyperelliptic curves of g=3 but also, can replace elliptic curves. In addition, in hardware implementation of applications with a lower security level like in groups with order 2128 , computations of hyper elliptic curves of genus g=4 are almost 1.46 times faster than that of hyperelliptic curves of g=2. It also uses the same efficiency as hyperelliptic curves of g=3. It is also noteworthy that compared with hyper elliptic curves of g=2, 3, hyperelliptic curves of g=4 are more appropriate to be implemented in embedded microprocessors than general processors. To gain a security level of 2128 , a hyper elliptic curve of g=4 can be defined on the finite field F . Thus implementing these curves on 32-bit processors will be really efficient. It will be more efficient than hyperelliptic curves of g=2 and almost equally efficient as hyperelliptic curves of g=3. Usually, when using cheap embedded processors, a lower security level will be needed. In practice, a group of the order 2128 will suffice. This security level is almost higher than that of RSA-512 [28-32].

V. Pairings on Hyper Elliptic Curves

Take C as a hyperelliptic curve of genus g defined on

F so that gcd (r, g ) = 1, rJ (F )| . Also, take r as a prime number. The embedding degree j (F ) related to r is the least integer number k so that r |(qk -1). In other words, F* includes the group n (the unit's r th roots).

q ^{k                                        r}

Some of pairing based protocol are in [5-10]. Another important parameter in pairing functions is called p - glogq value which is p =------ . This parameter is almost logr equal to the bit length of |j (Fq )| to the bit length of a subgroup of the order r. A Jacobin with a number of prime members has the least amount of p -value (p ® 1) . Hyperelliptic curves whose Jacobins have a small embedding degree and a subgroup with big prime order are appropriate to be used in paring functions. They are called pairing friendly [3, 13]. In practical application values of r > 2160 , k < 60 are needed. Also, as mentioned earlier, the best attack at the discrete logarithm problem is the p -Pollard algorithm which is implemented in a parallel way. Running time of this algorithm is

O (Jr) with r as the value of the biggest prime subgroup j (f ). For hyper curves of genus g=3, 4 there can be index calculus attacks complexities:

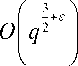
f         A

= O J ⁽ F q 1"

I          7

O q

-+s

with these respective

f          A= O J(Fq )ГI          7

To compare with the paralleled p -Pollard algorithm which depends on the subgroup of the order r, it can be said if p < - of g=3 and also p < — of g=4, then the index calculus attack reaches the upper boundary of the p -Pollard attack. However, the best algorithm to solve the discrete logarithm problem for hyper curves of genus g=2, 3, 4 have exponential running time. On the other hand, the best algorithm to compute the discrete logarithm in a finite field is the index calculus attack which has the sub- exponential running time related to the field’s size.

Therefore, in order to reach an equal security level in both groups (multiplication group resulted from a finite field and Jacobin group resulted from a hyper curve) the value of q k must be definitely larger than r.

Table 3. Embedding Degree for Genus 2-Hyper Curves with an Equal Security Level [28].

Security level (bit)	Size of subgroup (r)	Size of field expansion ( qk )	ρ ≈ 1	ρ ≈ 2	Embedding degree ( k )			ρ ≈ 8
					ρ ≈ 3	ρ ≈ 4	ρ ≈ 6
80	160	1024	6g	3g	2g	1.5g	g	0.8g
112	224	2048	10g	5g	3.3g	2.5g	1.6g	1.3g
128	256	3072	12g	6g	4g	3g	2g	1.5g
192	384	7680	20g	10g	6.6g	5g	3.3g	2.5g
256	512	15360	30g	15g	10g	7.5g	5g	3.8g

The table above shows examples of subgroup value, expanded field value, and the embedding degree size for an equal security level which are all held in relation r≈ qg/ρ . Subgroups of the prime order and expanded fields (with large discriminates) follow the NIST standard. The above table is based on g=2. For g=2, 3, 4, these procedures must be followed:

If the Jacobin order is almost prime (ρ ≈ 1) , then it is just required to arrange parameters in a way so that they can resist the index calculus attack. For g=3, the second column of the above table should be multiplied with and the fourth column at . For g=4, the second and 8                                   9, the fourth columns should be multiplied respectively at and . Embedding degree for super singular hyper curves of genus g=2 holds true in relation k ≤ 12 . For general hyper elliptic curves of genus g=2 in specific cases, it also holds true in relation k ≤ 12 . The quickest implementation of pairing functions has been offered for the pairing η which uses a super singular genus 2-hyper elliptic curve defined on a finite field with the discriminate 2. Embedding degree of this case is 12 .The results reached at by [28] exhibit that:

• •    Implementation of a pairing called h on genus 2-hyper curves has a similar function as implementation of the Tate pairing.

• •    The η pairing’s implementation on genus 2-hyper elliptic curves is much more efficient compared with that of h pairing.

• •    Implementation of the pairing η on genus 2-hyper curves is more efficient than implementation of the pairing η on super singular hyperelliptic curves defined on F .

• •    Computing the pairing function on genus 3-hyper curves is very inefficient than that of genus 2-hyper curves.

• •    Implementation time of a pairing function on genus 2-hyper curves defined on F is almost two times longer than implementation time of a pairing on hyper elliptic curves defined on F . To decrease this time

distance, it is essential to use super singular genus 2-hyperelliptic curves.

• VI. Conclusion

The current paper introduced hyper elliptic curves. It also offered comparisons between different types of these curves regarding their security and efficiency. Therefore, it can briefly be concluded that index calculus attack is possible for hyperelliptic curves of g ≥ 5 .So, they are not appropriate to be used in public key cryptography. In applications with no need of a high security level like WSN with low-cost embedded processors that use cryptography algorithms with smaller key size, hyper elliptic curves of genus g = 2,3,4 can be applied.