A Study on Contributory Group Key Agreements for Mobile Ad Hoc Networks

Published Online April 2013 in MECS

A Mobile Ad hoc Network (MANET) consists of a collection of wireless mobile nodes that are capable of communicating with each other without the use of any centralized administration or network infrastructure. With the explosion of cheaper, smaller, and more powerful mobile devices, Mobile Ad hoc Networks (MANETs) have become one of the fastest growing areas of research. This new type of self-organizing network combines wireless communication with a high-degree node mobility. The union of nodes forms an arbitrary topology. This flexibility makes them attractive for many applications such as military applications, where the network topology may change rapidly to reflect a force’s operational movements, and disaster recovery operations, where the existing infrastructure may be non-operational. The ad hoc selforganization also makes them suitable for virtual conferences, where setting up a wired network infrastructure is a time-consuming and high-cost task.

Nodes on MANETs use multi-hop communication: nodes that are within each other’s radio range can communicate directly through wireless links, whereas those that are far apart must rely on intermediate nodes to act as routers to relay messages. Mobile nodes can move, leave, and join the network, and routes need to be updated frequently due to the dynamic network topology.

In the literature there are number of protocols proposed for MANET routing. There are communication overheads in detecting optimum routes with power saving and detection of malicious nodes or captured nodes. The basic requirements for a Secured network protocol for MANETs are – Confidentiality, Integrity, Availability and Non-repudiation. Issues and challenges for MANETs in security provisioning are – Dynamic Topology, Scalability, Autonomous, Poor Transmission Quality, Bandwidth Optimization, Device Discovery, Infrastructure less and Self Operated, Limited Resources, Limited Physical Security, Ad hoc Addressing, and Topology Maintenance.

The security attacks can generally be distinguished into two types – Passive and Active attacks. A MANET should provide a reliable and secure communication mechanism as nodes join or leave the network and their time of association with the network cannot be predicted. The data traffic in the ad hoc network travels through multiple hops routed through a vulnerable wireless medium, enhancing the security risk.

MANETs are vulnerable to diverse types of security attacks as the transmission takes place in the open medium and constraint resources. Portability has made devices each time smaller, with resource limitation, and thus easy targets for overload attacks [1, 2]. The network decentralization, absence of support infrastructure and the dynamic topology increase the vulnerability to many attacks as impersonation attacks, Sybil attacks [3], selective forwarding, black-hole, wormhole attacks [4, 5], among others. Many solutions have been proposed for security problems on ad hoc net-works [1, 5, 6, 7]. In general, these solutions work in the preventive or reactive way and apply mechanisms and techniques to protect basic protocols and applications. However, techniques and mechanisms are used for a specific goal, being effective to one given case, but inefficient to others. Moreover, all existent techniques and mechanisms are themselves incapable of individually defending against all types of attacks and intrusions.

This paper studies the routing protocols for MANET based on the Group Key Management. The rest of the paper is organized as follows. Section II introduces the Group Key Management. Section III discusses the Operations and Metrics for Group Key Management. Section IV focus on classification of Group Key Management schemes. Section V discusses on Contributory Group Key agreements for MANETS. Section VI is challenges and future directions for key management. Finally Section VII represents the conclusion of this paper.

II Introduction to Group Key Management

Key management is a central part of the security of MANETs. In MANETs, the computational load and complexity for key management are strongly subject to restriction by the node’s available resources and the dynamic nature of network topology. The fundamental goals of key management systems are to manage the keys used in the networks and simultaneously prevent the improper use of legally issued keys, such as the unauthorized modification, disclosure, or replaying keys, as well as the use of out-of-date keys, etc.

Cryptographic algorithms are security primitives that are widely used to provide the services like authentication, data integrity, non-repudiation and data confidentiality to establishment a Key Management Protocol. A group key is a piece of input information for cryptographic algorithms. If it was released, the encrypted information would be disclosed. For secure group communication in an Ad hoc network, a group key shared by all group members is required. Key management for large dynamic groups is a difficult problem because of scalability and security. Each time a new member is added or an old member is evicted from the group, the group key must be changed to ensure backward and forward security. Backward security means that new members cannot determine any past group key and discover the previous group communication messages. Forward security means that evicted members cannot determine any future group key and discover the subsequent group communication information. The group key management should also be able to resist against colluded members.

Mobile nodes come together to form an ad hoc group for secure communication purpose. A key distribution system requires a trusted third party that acts as a mediator between nodes of the network. But in Ad hoc networks characteristically do not have a trusted authority. Group Key Agreement means that multiple parties want to create a common secret key to be used to exchange information securely. Furthermore, group key agreement also needs to address the security issues related to membership changes due to node mobility. The membership change requires frequent changes of group key. This can be done either periodically or updating every membership changes. The changed group key ensures backward and forward secrecy.

With frequent changes in group memberships, the recent researches began to pay more attention on the efficiency of group key update. Group key agreement is a building block in secure group communication in Ad hoc networks. The Group Key Management scheme includes important phases like – key generation phase, key distribution phase, and frequency-based key update phase.

According to recent literature, the centralized approach is regarded as inappropriate for MANETs because of the dynamic environment and the transient relationships among mobile nodes. Most researchers prefer the decentralized trust model for MANETs. Several decentralized solutions have been proposed in recent papers with different implementations, such as how the CA’s responsibility is distributed to all nodes, or to a subset of nodes.

III Operations and Metrics for Group Key Management

• A.    Dynamic Group Key Operations:

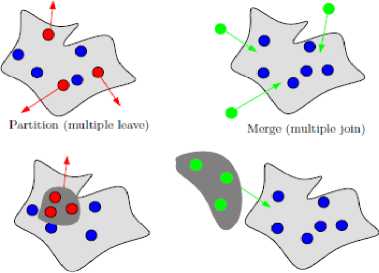
In order to accurately and fairly evaluate group key management protocols, definitions are needed that explain the operations used by the main group key management protocols. In the literature, it was found that there are eight major operations that were essential for establishing and sharing keys across the dynamic group. The Fig. 1 shows these operations.

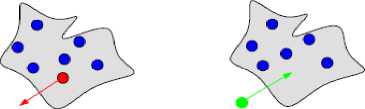
Leave                                  Join

Partition (subgroup)                    Merge (group)

Figure 1. Group key operations

Initialization operation – This is the initial creation of the group key and organization of the key management infrastructure

Join – This operation brings a new member into the existing group.

Mass join (Mass add) – This operation allows many new members to be added to an existing group simultaneously when these new members have not already formed a group of their own.

Merge (group fusion) – This operation, as opposed to mass join, is used when another group is combined with the existing group to become a new group.

Leave – His operation is used to remove a member from the group.

Mass leave – This operation is used when multiple members are simultaneously removed from the existing group.

Split (partition, or group fission) – This operation, different from mass leave, occurs when a single group is divided into two or more component groups.

Key refresh – This operation is to prevent the secret key from being used for a long time. Moreover, to prevent an adversary from breaking in, we should refresh the original key and generate a new secret key periodically.

• B.    Performance Metrics:

The following attributes are Performance metrics used to evaluate the efficiency of contributory key management protocols:

Number of rounds – The protocol should try to minimize the number of iterations among the members to reduce processing and communication requirements.

Number of unicast messages – This is number is the sum of the number of messages every member sends to other single members in the group per operation. This number is useful for determining total communication and is important if many or all nodes are on the same network collision domain, thus forcing these messages to be sent sequentially rather than simultaneously.

Number of broadcast messages – This is the sum of the number of messages sent by each member to all the other members in the group per operation. Since the messages go to all members of the group, it greatly affects total communication costs depending on the underlying network topology.

Number of messages – This is the sum of the number of unicast messages and broadcast messages. This number is used to determine the total time of communication in an underlying broadcast network The overhead introduced by every message exchanged between members produces unbearable delays as the group grows. Therefore, the protocol should require a minimum number of messages.

Processing during setup – Computations needed during setup time. Setting up the group requires most of the computation involved in maintaining the group, because all members need to be contacted.

DH key – Identify whether the protocol uses Diffie– Hellman (DH) [Diffie and Hellman 1976] to generate the keys. The use of DH to generate the group key implies that the group key is generated in a contributory fashion.

Number of sequential exponentiations – During an operation there will be a series of computationally expensive cryptographic operations (such as modular exponentiation used in the DH protocol). The protocols in the literature often require the results of one cryptographic operation prior to the execution of another. This metric represented the worst case scenario, the longest sequence of dependencies of these cryptographic calculations in the operation.

Number of signatures – This is the sum of digital signatures used in every round. In every round, the node initiating the operation sends one digital signature.

Number of verifications – Given that each message needs to be verified, the number of verifications is equal to the number of messages; however, several verifications can occur in parallel so care is needed with the number of sequential verifications that must occur during an operation

• IV Group Key Management Agreements

The Group key management protocols can be approximately classified into three categories [8] as

• •    Centralized Group Key Distribution (CGKD)

• •    De-centralized Group Key Management (DGKM)

• •    Contributory/distributed Group Key Agreement (CGKA)

• A.    Centralized Group Key Distribution (CGKD):

In CGKD, there exists a central entity called as group controller (GC) which is responsible for generating, distributing, and updating the group key. One of the famous CGKD scheme is the Logical Key Hierarchy (LKH). This was proposed by several research groups nearly at the same time, followed by many researchers proposing improvements and enhancements [9, 10, 11, 12, 13, 14]. Some of the Centralized Group Key Management protocols are

• •    Group Key Management Protocol

• •    Logical Key Hierarchy

• •    One-way Function Tree

• •    One-way Function Chain Tree

• •    Hierarchical a-ary Tree with Clustering

• •    Centralized Flat Table

• •    Efficient Large-Group Key

• B.    De-centralized Group Key Management (DGKM):

The DGKM approach involves splitting a large group into small subgroups. Each subgroup has a subgroup controller which is responsible for the key management of its subgroup. Subgroup controllers are also in charge of relaying encrypted data messages. The first DGKM scheme was IOLUS [15]. There followed some improvements and hierarchical group key management schemes [16, 17, 18]. Some of the De-centralized Group Key Management protocols are

• •    Scalable Multicast Key Distribution

• •    Iolus

• •    Dual-Encryption Protocol

• •    MARKS

• •    Cipher Sequences

• •    Kronos

• •    Intra-Domain Group Key Management\

• •    Hydra

• C.    Contributory Group Key Agreement (CGKA):

The CGKA schemes involve the participation by all members of a group towards key management. Such schemes are characterized by the absence of the GC. The group key in such schemes is a function of the secret shares contributed by the members. Being contributory in nature, the distributed schemes help in the uniform distribution of the work-load for key management and eliminate the requirement for a central trusted entity. Typical CGKA schemes include binary tree based ones [19] and n-party Diffie-Hellman key agreement [20, 19, 21]. Some of the Contributory Group Key Management protocols are

• •   Burmester and Desmedt Protocol

• •    Octopus Protocol

• •   Group Diffie–Hellman Key Exchange

• •   Conference Key Agreement

• •    Distributed Logical Key Hierarchy

• •    Tree–Based Group Diffie–Hellman

• •    Skinny Tree

• •   Distributed One-way Function Tree

• •   Diffie–Hellman Logical Key Hierarchy

• •    Distributed Flat Table

V Contributory Group Key Agreements

MANETs can be used in all those situations where there is no time or resources available to setup a backbone network or infrastructure. With their increasing usage, Secure Group Communication (SGC) over such networks becomes vital. In MANETs, since there is no pre-defined/fixed infrastructure, a Central Authority (CA) is not usually available, and there are generally equivalent levels of power and trust among the participating members. A contributory group key agreement scheme is most appropriate for SGC in this kind of environment. Several group key management schemes have been proposed for SGC in wireless networks. The Fig. 2 shows the required components for implementing contributory group key management schemes.

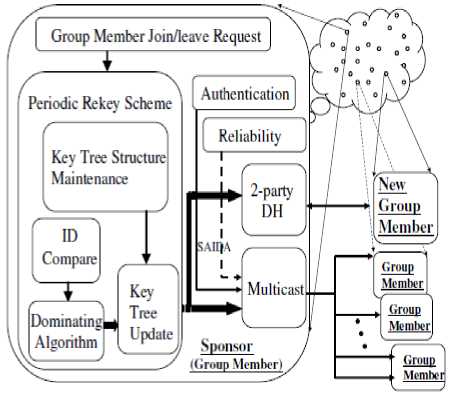
Figure 2: Contributory Group Key Management

A. Burmester and Desmedt (B-D) Protocol:

BD is a distributed group key management scheme proposed by Burmester and Desmedt [22]. It is an extension of the Diffie-Hellman key distribution system. The group key can be calculated in three rounds which are as follows:

Round 1 – Broadcast the partial keys

Round 2 – Calculate key material

Round 3 – Compute the group key

However, when a new group member joins or when a group member leaves, most of the group members need to refresh the random session and follow the steps mentioned above one by one. Therefore, this scheme requires high resources.

• B.    Octopus Protocol:

This protocol was proposed by Becker and Wille [1998]. This protocol is also based on DH key exchange protocol. In Octopus, the large group of n members is split into four subgroups namely, A, B, C and D. In every sub-group, there is one group member leader available, namely M A , M B , M C or M D , respectively. The leader member in each subgroup is responsible for collecting contributions from all its subgroup members and calculating the intermediary DH value I A (or I B , I C , I D ,). Then, the four group leaders launch the DH scheme to compute group key G and send G back to every sub-group member. Specifically, the group is split and the intermediate values are computed as below (r i is the contribution of group member M i ): Subgroup A includes group members M 1 … M n =4; the leader of sub group A, calculates I A = II 1ri. The sub-group leader, for example, A, should has a secure channel between every other subgroup member. Via these channels, A can obtain r1,…, rn/4 one by one. The same applies to B, C, or D. After the completion of this procedure, group key G can be computed as described below.

• C.    Group Diffie–Hellman Key Exchange (GDH):

GDH is a group key distribution scheme proposed by Steiner, Tsudik, and Waidner [23] in three versions. GDH extends the two-party Diffie-Hellman key exchange protocol into a group operation. GDH actually contains three key distribution schemes that are extended from the DH protocols. In GDH.1 and GDH.2, the overhead of computation is quite considerable due to the total of O(n²) exponentiation calculations. GDH.3 has been proposed to reduce this, in which every member only needs to perform a constant small number of exponentiation computations.

The first stage involves collecting contributions from all group members and user U n-1 obtains

M i N k I ^k n: I

g

, n - 1]}

In the second stage this value broadcasts to all other group members. At the third stage , every user U i (i ≠ n) factors out its own exponent and forwards the result to the last user U n . At the final stage , U n collects all inputs from the previous stage, raises every one of them to the power of N n and broadcasts the resulting n-1 values to the rest of the group. In the end, every group member has a value of the form

M { N *1 k ^el I,n ]^л k * i } ^g

and can easily compute the group key K n .

An important drawback of GDH.3 is that the success or failure of the group key generation depends on the performance of the last member in the group. The last group member receives n messages and needs to perform n exponentiations computations. This requires the member to have plenty of storage space and strong computational power. However, not every member has such power, especially in wireless networks. As the group size increases, the time taken for the key generation significantly increases and this causes a slow response to membership changes. Member addition and deletion can be handled easily in this scheme.

• D.    Conference Key Agreement (CKA):

Boyd [24] proposed a protocol for conference key agreement (CKA) where all group members contribute to generate the group key. The group key is generated with a combining function: K = f ( N 1 , h ( N 2 ), … , h ( N n )), where f is the combining function, h is a one-way function, n is the group size and Ni is the contribution from group member i . The protocol specifies that n-1 members broadcast their contributions ( Ni ) in the clear. The group leader, for example U 1 , encrypts its contribution N 1 with the public key of each (n-1) group member and broadcasts it. All group members who had their public key used to encrypt N 1 can decrypt it and generate the group key.

• E.    Distributed Logical Key Hierarchy (D-LKH):

This approach is proposed by Rodeh [25] as an extension to Centralized Logical Key Hierarchy without a support of a centralized server. In this approach, the Group Controller (GC) is completely abolished and the logical key hierarchy is generated among the members, therefore there is no entity that knows all the keys at the same time. In this scheme, every group member plays a symmetric role. This solution utilizes the logical tree which has two groups of members namely, left sub tree L and right sub tree R. Member M L is assumed to be L’s leader and member M R is R’s leader. Every group member in L agrees on a shared key K L , and those in R, a shared key K R . The protocol used to agree on a mutual key goes groups L and R as follows:

• 1.    M L , the group leader of L, chooses a new key K LR and sends it to the group leader of R, M R , using a secure channel.

• 2.    M L encrypts K LR with key K L and multicasts the cipher text to its group members in L. M R encrypts K LR with key K R and multicasts the cipher text to its group members in R.

• 3.    All members within L and R receive the cipher text and decrypt the group key, K LR .

• F.    Tree–Based Group Diffie–Hellman (TGDH):

In [26][19] Kim et al. has proposed a contributory group key agreement protocol named Tree-based Group Diffie-Hellman (TDGH) as an extension to the two-party DH protocol. This brought two important trends in group key management together viz., 1) key trees to efficiently compute and update group key and 2) Diffie-Hellman key exchange to achieve secure and fully distributed protocols. TGDH protocol suite has four protocols: join, leave, merge, and partition. These share a common framework with the following features: • Each group member contributes its equal share to the group key, which is computed as a function of all shares of current group members.

• •    This share is secret (private to each group member) and is never revealed.

• •    As the group grows, new member’s shares are factored into the group key but old member’s shares remain unchanged.

• •    As the group shrinks, departing member’s shares are removed from the new key and at least one remaining member changes its share.

• •    All protocol messages are signed, time-stamped, sequence-numbered and type-identified by the sender.

In TGDH the group key is derived from the contributions of all group members. All members maintain an identical virtual binary tree that may or may not be balanced. Each member is associated with a leaf node in the key tree. Members use Diffie-Hellman protocol to generate the keys along the path from its leaf node to the root.

In this protocol group member can take on a special sponsor role which involves computing intermediate keys and broadcasting to the group. Each broadcasted message contains the sender’s view of the key tree which contains each blind key known to the sender. Any member in the group can unilaterally take on this responsibility, depending on the type of membership event. In case of join or merge, all group members identify a unique sponsor. This sponsor is responsible for updating its secret key share, computing affected [key, blind key] pairs and broadcasting all blind keys of the new tree to the rest of the group. In response to a leave or partition, all members update the tree in the same manner. Group partition results in a smaller tree since some leaf nodes disappear. As a result, some subtrees acquire new siblings; therefore, new intermediate keys and blind keys must be computed through a Diffie-Hellman exchange between the new sibling’s sub-trees.

TGDH is operational efficient in communication and computation, because only one round is required to calculate the group key. The sponsor only needs to send one keying message. The keying message contains log 2 n blinded keys ( n is the number of users in the group). The members in the group perform, at most, log 2 n exponentiations computation to reach the group key. But, this protocol relies on a sponsor. If the sponsor fails, the whole key updating procedure stops. And also, each member needs to maintain an identical virtual binary tree. Substantial, storage space is required to maintain such a tree structure for a large group.

• G.    Skinny Tree (STR):

This is an extension of one of the earlier tree-based group key management by Steer et al. [27] proposed by Kim [19] to handle membership events. This scheme utilizes an unbalanced key tree in which every leaf node represents a group member. All intermediate nodes play a management role. In this the height of the key tree is always ( n -1), as opposed to log( n ) in TGDH. All other features of the key tree are the same as in TGDH.

Every group member M i should generate a random secret r i and calculate its leaf node’s blinded key BK = α^ri. In the first round, every member broadcasts BK = α^ri where 1 ≤ i ≤ n and n is the group size. To handle group members joining, STR adds a new leaf node to represent the new member. This new leaf node is treated as the current root’s sibling and a new root node is created which works as the former root and the new member's parent. The group member representing with the leaf node right below the new leaf node is selected as the sponsor. When a group member leaves, the leaf node representing the leaving group member and the corresponding sibling node are deleted. The group member represented by the leaf node right below the leaving member’s leaf node is treated as the sponsor. Finally, the updated blinded keys are multicast and every other group member can calculate the new group key. STR reduces the number of rounds needed to update the group key as compared with TGDH.

• H.    Distributed One-way Function Tree (D-OFT):

Dondeti et al. [28] proposed an approach using logical key hierarchy in distributed fashion as an extension to One-way Function Tree (OFT). As in TGDH, D-OFT uses the binary key tree for group generation and group management. Every group member is trusted with access control and key generation. A member is responsible for generating its own key and sending the blinded version of this key to its sibling. The blind key is calculated as below:

KB = g(K)                            (3)

where K: node key; K B : blinded key; g: one way hash function;

The leaf node’s key is generated by the group member and the intermediate node key is computed according to the formula:

K i = f (g (K left_child (i) , K right_child (i) ))       (4)

where f: mix function to mix together the two parameters.

The leaf member calculate the group key by knowing of all node keys on its key path and all blinded keys on its sibling key path. When group members join/leave, new contributions of the changing member's sibling should be refreshed and the corresponding node key and blinded key on its key path should be updated. A secure channel is assumed between the group members to send the updated node key and blinded key. This method is computationally efficient than TGDH, since the one-way hash function rather than the exponential operation is used to calculate the blinded key and node key. The secure channel between group members is a limit for this proposal.

• I.    Diffie–Hellman Logical Key Hierarchy (DH-LKH):

Perrig [29] and Kim et al. [26] also used a logical key hierarchy to minimize the number of key held by group members. The difference here is that group members generate the keys in the upper levels using the Diffie–Hellman algorithm rather than using a oneway function. The tree is built recursively from bottom to up. Initially, each member M i generates a random r i as a secret key associated to its leaf. To build upper level of the tree, two members: one as a leader of a left sub-tree and another one as a leader of a right sub-tree, broadcast their respective DH computations and hence allow to all the members to calculate the group key corresponding to the root of the tree. Because of the logical key hierarchy the number of key calculations are reduced from the order of O ( n ) to O ( logn ).

• J.    Distributed Flat Table (DFT):

Waldvogel et al. [30] extends further its solution, proposing to use the flat table in a distributed (DFT) fashion with no Group Controller (GC). In this scheme, no member knows all the keys at any time. Each member knows only the Key Encryption Keys (KEKs) that it is entitled to. The inconvenience in this is that a joining member is obliged to contact a group of members to get all the keys needed. Furthermore, since many members could be changing the same key at the same time, there could be serious delays in synchronizing the keys.

• VI    Open Challenges and Future Directions

Security is an important feature that determines the success and degree of deployment of MANETs. Key management is in the central part of any secure communication and is the weakest point of the security. Security of MANETs is more challenging because of the host mobility, shared wireless medium, resource constraint of physical devices, and lack of a fixed and trustable control point. Designing a key management system is a difficult problem that has received increased attention recently. The current research on key management in MANETs is still at its early stage. The security of group communication involves the management of group keys. Most contributory group key distributions are based on DH protocol with different implementations. Recent references paid more attentions to contributory and collaborative group key agreement, for example: [31–35], etc.

In [31] Shanyu proposed a Communication– Computation Efficient Group Key Algorithm (CCEGK) to provide efficient communication and computation, addressing performance, security and authentication. This group key management algorithm based upon two preceding group key management algorithms, EGK and TGDH. This algorithm fully implements an initialization operation and presents two mass leave operations, mass leave-balanced, and mass leave-imbalanced, while the TGDH algorithm only details a mass leave-imbalanced. TGDH and STR do not implement a balance operation, and CCEGK does.

R. Dutta and R. Barua [32] have proposed a new protocol named as DB protocol, which is an extension to the Burmester-Desmedt (BD) protocol. This has important differences as – simple key computation, less number of rounds for authentication, ability to detect corrupted group members and reduced computation complexities.

Sun and Liu [33] have presented a contributory group key agreement with a new logical key tree structure called PFMH. This scheme needs O(1) rounds of two-party DH for single user join event and O(log n) for single user leave event. This achieves lower rekeying cost than the existing tree-based contributory group key agreements.

In [34] Mao and Sun have proposed a Join-Exit-Tree (JET) key management framework for better time efficiency during member join and departure. This framework has reduced the time for a member join or departure event to O(log (log n)) from O(log n).

Balachandran et al. proposed contributory key agreement protocol for MANETs, called Chinese Remainder Theorem and Diffie-Hellman (CRTDH) [35]. This has shown solutions for two important problems of Secure Group Communication – requirement of member serialization and existence of central entity.

• VII    Conclusion

In this paper we have studied contributory group key management protocols for Secure Group Communications for Mobile Ad-hoc Networks. Based on different assumptions, many key management protocols have been proposed for MANETs. But none of the protocols can be used as a universal solution for all classes of Mobile Ad-hoc groups. A protocol should be chosen according to the expected dynamic behavior in the group, required level of the security for the application, and priority between computation and communication constraints. All key management approaches are subject to various restrictions such as the mobile device’s available resources, the network bandwidth, and MANETs’ dynamic nature. An efficient key management protocol for MANETs is an ongoing hot research area.