A Survey and Theoretical View on Compressive Sensing and Reconstruction

Published Online April 2016 in MECS DOI: 10.5815/ijigsp.2016.04.01

Due to Nyquist rate much of the signal processing has moved from the analog to the digital domain. As a result of this success the amount of data generated by sensing systems has grown from a smaller number to a larger number. Unfortunately in many important and emerging applications the resulting Nyquist rate is so high that we end up with far too many samples and it may be too costly or even physically impossible to build devices capable of acquiring samples at that necessary rate. After 20th century onwards amount of data generated grows in super exponential form which means data growth was about 30 to 40% per year. This amount of data generated exceeds the total storage available in the word. This is called DATA DELUGE problem. Even though storage capacity is increased but transmission rate or channel rate is not increased up to the mark. Rate of date generation is much larger than rate of increase in transmission rate. Compressive Sensing concept [2], [3], [5] and [11]

depicts that one can recover certain signals from less number of samples than Nyquist rate. Compressive Sensing is asymmetric which means it consist of dumb encoder and smart decoder. But it is a stable system [9]. This paper contains seven sections. First section includes introduction and data deluge problem, where as second section explains few fundamental facts such as Sparsity and Normed vector spaces. Third section contains relationship between CS theory and sampling theory. Fourth section contains theory related to design of sensitive matrix. Fifth section explains reconstruction algorithm in the form of graphical methods. Last two sections contain proposed work, literature survey and conclusion with future work.

• II.    Fundamental Facts of CS

• A.    Sparsity Property

  Analog

  
  

  Sample

  
  

  Compress

  
  

  К «N

  
  

Using Transform Encoder

Fig.1. General Compression.

General compression as shown in Fig.1 when analog object is uniformly sampled then it generates 'N' number of samples. These samplers are large in number and reduced using Transform coders. These coders compress the signal in to smaller numbers 'K' by converting from one domain (basis) in to other domain. Suppose the information is in image domain of dimension ‘N’ then it is converted into Wavelet or DCT (Discrete Cosine Transform) domain of dimension‘N’. After analysing ‘N’ dimensional wavelet or DCT samples it is found that most of the coefficients are very small and some coefficients (K) are large. Small coefficients are truncated and remaining coefficients are used for further processing. Finally signal is compressed from dimension ‘N’ to dimension ‘K’ which contains all the intrinsic information about the object. This concept was almost used in JPEG coder. This property is called sparsity and representation of analog object into few numbers like wavelet or DCT domain is called sparse representation [12]. All kinds of signals are naturally sparse in nature either in sampled domain or in other domain. Most of the practical signal contains sparsity nature. Even noise itself exhibits sparsity property. Sparse vector contains all zeros and few (K) nonzero entries. This property is represented mathematically using matrix called sparse matrix. This is defined as “any matrix with enough zeroes values that it pays to take advantage of them”. In compression these values are truncated and thus signal dimension is reduced. In time domain sparse signal is a simple vector of length ‘N’ in which only ‘K’ elements has nonzero value which is called as Canonical Sparse. When these elements are sorted they will obey the power law decay. Sparse signal always live in high dimensional or infinite dimensional spaces which are aligned with coordinate axis. For example if sparse vector contains three elements and one of them is zero means zero can be located any location of the vector. It seems to be very simple but these elements live in three separate two dimensional spaces which are aligned with coordinate axis as shown in Fig. 2 and are orthogonal to each other.

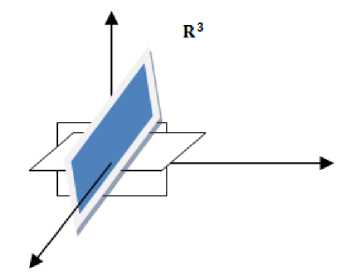
Fig.2. Three dimensional subspace-R3 (N=3, K=1)

A set of sparse signal is point in million dimensional spaces that live along some (ex: 10000) sub dimensional space as shown in Fig.3 which are aligned with coordinate axis.

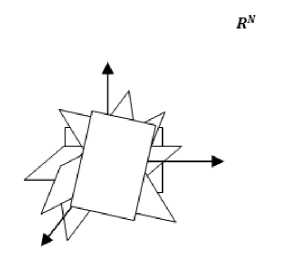
Fig.3. Million Dimensional Space

Compressible signal is a set of sorted elements of sparse vector of length ‘K’ . Each element of a vector is either wavelet or DCT coefficients (Ci) . Sort the vector coefficient according to its magnitude then it follows the power law decay property. A set   {Øi} where i = (1,2,3......n) is wavelet or DCT basis for RN are linearly independent. This implies that each vector in the space has a unique representation in the form of linear combination which is depicted in equation (1). XϵRN, there exist coefficients { Ci } where i = (1,2,3......n) such that x = ∑in=1 CiØi                         (1)

It means signal is sparse in some other domain (Øi) with value Ci then time domain signal can be expressed using above formula which is called as dual basis formula. Let

Fij denote the n x n matrix with column given by ø i and F_i denotes entries then complete signal F can be completely represented by equation (2).

x = Фc(2)

Two wavelet or DCT bases are said to orthonormal if they satisfy following condition as shown in equation (3).

(Øi,Øj) ={10,,   ii≠=jj

An orthonormal basis has the advantage that the coefficient F can be easily calculated from equation (4).

c = ФTx.(4)

By using the sparsity concept if we express only those sets which are linearly dependent then those basis are called as frame. Naturally dimension will be reduced from F to F and matrix dimensions will be reduced d x n such that all sparse xϵR^d . This concept is extended in CS for signal reconstruction.

• B.    Normed Vector Space

Every system can be modeled in a linear fashion. Each system process the signals to produce proper results, therefore signals should be in linear form. Linear property indicates that when we add signal it should produce new kind of signal. In vector space using length, angel and distance of each signal is used to estimate the proper value. Mathematically signals are viewed as vectors in an n-dimensional Euclidian space, denoted by RN . Using Lp norms these signals are analyzed. In mathematics, the Lp spaces are function spaces defined using a natural generalization of the form p-norm for finite-dimensional vector spaces. These Lp norms are defined as shown in equation 5.

(∑ⁿ |x|^P) P¹ , p ∈ (1, ∞);

‖x‖ p = 1     max IxI, P = ∞                 ⁽⁵⁾

i = 1,2,…n

Norm of a vector is calculated by taking Pth power of each element and adding them. Usually Normed vector space is concerned to discrete and finite domain signals. If P = 2 it is energy and P < 1 it is called as bounded norm or quasi norm which is highly non convex. It means if we connect two points using straight line then that line will not touches any other point which is defined in vector.

The result will be a new kind of signal means no other signals exist in between them.

P=1  P=2

P = да

P = 1/2

Fig.4. Unit Sets in Two Dimensional (R2) for the LP norms

Quasi norm can be defined by equation (6).

||x|| 0 “ |supp(x)|where supp(x) = {i: x i ^ 0 }

This quasi norm denotes the coordinates of sparse signal which is having nonzero coefficient. These Lp quasi norm exhibits different properties for different values of. Strength of the signal is measured using above Lp norms. If 'x' is element of vector defined in two dimensional spaces. Reconstruction of ‘ xc ’ in one dimensional affine space is to minimize approximation error (x — xc) using Lp norms. The choice of will play major role in minimizing the error. Larger value of will increase the error. Bounded norm as shown in Fig. 5 means less than one closely estimate the value. In CS same concept is extended to higher dimensional space to reconstruct the signal.

important points are to be highlighted whenever mathematical model is designed for sampling process. First one is information preservation and second one is reconstruction. Since Y = X naturally information is preserved and by using some trivial operation will gives back from.

Sampling, processing without aliasing and reconstruction using SINC interpolation are linear only compression that is converting ‘N’ to ‘K’ is non linear. In compressive sensing we are not interested in all the samples we are interested in sparse samples. Sampling model is modified to incorporate compressive theory.

B. Compressive Theory

Compressive sensing is all about to cut off the middle concept that is sampling process and develop new type of device which captures the light coming from object and straight away to 'M' measurement [8] which is as same as 'K' sparse signal as shown in Fig. 7 . When data is compressible, it can be directly acquire a few representations with little information loss which are negligible.

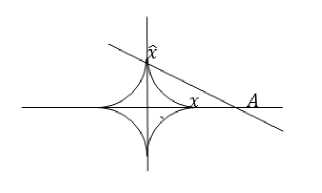
Fig.5. P=1/2 Bounded P Norm

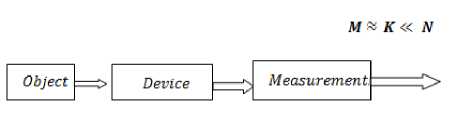
Fig.7. Block Diagram of Compressive Sensing

III. Compressive Sensing

A. Sampling Theory

Actual sampling is operating on analog signal which is essentially a linear identity operator. This operation can be modeled using matrix Y = Ф X as shown in figure Fig. 6.

This dimensionality reduction can also be represented as Y = ФX where ^T.. is MXN which contain information related to sparse measurements as shown Fig. 8 such as co ordinates, coefficient and basis. These sparse signals are obtained by transforming in to new basis and keeping large coefficients and truncating small coefficients. The number of compressive measurements must be close to . It means M « K « N . These measurements are sparse signal. Each measurement carries same amount of information which is called as democratic [10]. In CS mathematical model we are not multiplying by big identity matrix but we are multiplying by short matrix. Present CS is all about discrete and finite system. We are using non adaptive measurement which means they do not depend on previously acquired measurements. CS work starts by

N X 1

Y y1 y2

У3 y4

Ф = I. N X N Identity matrix

X x1 x2 x3 x4

N X 1

LynJ

L0

1-1

xn

Fig.6. Sampling Model

'X' is a analog signal and 'Y' is digital signal which is obtained by multiplying by identity matrix on analog signal. Since operator is linear identity matrix then samples are as per Nyquist rate and Y = X . Two

assuming measurements are available and by how to acquire measurements.

ignoring

w x 1

Fig.8. Mathematical Model of CS Measurements

Since we are interested in only sparse measurement therefore sparse matrix is too short so that only sparse samples will be extracted from analog signal 'X' . Now for

this CS model we have to verify information preservation. Since 'Ф‘ is too short and it does not have rank 'n' so information is not preserved. There are infinitely other 'x' which will give exact same 'y' which means X = Ф^т Y does not give unique solution. Therefore same mathematical model is modified to incorporate information preservation. Since 'X' is analog signal which contain 'K' sparse signal and in CS importance will be given to sparse signal.

Arbitrary Columns

AfXl

-yl" >2 уз.

Ф^ Ф^ Ф;/

Ф^ Ф^ Ф^' ф^ ф^ ф .

хТ х2 .хЗ.

КХ 1

Fig.10. Sparse Matrix Obtained Using RIP

M X 1

Y

У1 y2

ym.

Ф M X к

Ф 11

Ф 21

Ф 12

Ф ₂₂

Ф 13

Ф 2 3

matrix

Ф 14

Ф 24

. Ф М1   Ф М2   Ф М3   ^Ф M4

Ф 1K ^Ф 2K

Ф MK.

X ■ xF x2 . xk.

К X 1

Assume that two sparse signal located in 'K' dimensional sub space with some Euclidian distance in Rⁿ .

R^w Mapping R^M

Fig.9. Modified Mathematical Model of CS Measurements

First key realization is if we assume 'X' is sparse signal then 'Y' is a linear combination of 'K' columns which are corresponds to the coordinates of ‘X' . CS model is modified by including M X K sparse matrix as shown in Fig. 9 . But it is difficult to identify columns of sparse vector since we do not know where the big coefficients are present. In practice it is very complex. If we are able to identify 'K' columns then it is a very simple problem. Second key realization is to design better sparse matrix of dimensions M X K such that it should have rank 'K' or select 'K' columns which are orthogonal to each other.

• IV. Design of Sensing Matrix

This design is based on three important matrix properties

• •    Null Space Property

• •    Restricted Isometric property

• •    Bounded Coherence.

For recovery there should not be two vectors x, x' such that Фx = Фx' because it would be impossible to differentiate among vectors from single measurement. Null space satisfies above requirement since null space means no vectors which are defined by equation (7).

Ч(Ф) = { г:Фг=0}          (7)

Using null space property it is proved that for any yeRm there exist at most one signal x e Xk such that y = Фх if and only if spark (Ф) > 2K. Spark of matrix is defined as smallest number of columns which are linearly independent. Critical design problem of compressive sensing is to design Ф of dimension M X N such that if we take arbitrarily columns out then it should have rank and these columns should be orthogonal to each other. This is called Restricted Isometric Property [6], [7].

Structural representation of designed Ф is as shown in Fig. 10 for K = 3 and M = 3 . Where sparse matrix contains coefficient values which are taken randomly which means value of 'i' and 'j' are any random values.

X1and X2

Fig.11. Geometrical Representation of Information Preservation

Ф x1 and Ф x1

When it is projected means mapping from R^N to R^M (dimensionality reduction) as shown in Fig. 11 using Ф then above two points will be located at same distance apart. This is nothing but distance preservation and indirectly it is information preservation. RIP ensures that Hx1 - x2H2 » HФx1 - Фx2H2 which means information preservation. But it is too complex and too lengthy because we have to repeat taking arbitrarily F_i columns from M x N matrix for every possible combinations means N^K times and out of all selection we have to find every possible 'K' column which obeys RIP property. Since 'N' are million (Mega Pixel) dimensions so it is too complex and too lengthy. But some mathematician reduced the complexity by deriving a formula (8) for random matrix which is called as randomized technique [14]. Most of the random matrix (Gaussian matrix, Bernouli etc) have high probability to exhibits RIP property as long as following formula holds

M = O(Klog( N ))«N          (8)

Number of measurement grows linearly by 'К' and logarithmically by 'N' . We can preserve information in signals by acquiring them by randomized sensing. Instead of sampling, linear measurements are taken by random set of weights applied over entire signal and adding them to construct the 'Y' which is all about information preservation in CS. Coherence (9) is one of the properties of sparse matrix which enables us to recover the signal. It is defined as “largest absolute inner product between any two columns of sparse matrix.

ц(Ф) = max |< Ф j ¹ for 1 < i < j (9) №l|2 |Ф₎|2

This coherence will define the range that is ц(Ф) e

N-M

IJ m(N-1)

Solution using l₂ X = (Ф^тФ) ¹ Ф^TY       (11)

1] .If N » M then lower bound becomes ^ (Ф) >

-=. Since is million dimensions it is difficult to find out VM

all possible columns which are having RIP property. Therefore initially it is mentioned too complex and too lengthy but now because of coherence property complexity is reduced by defining the range. It means signal which is to be recovered is somewhere in that defined range. These techniques are used in Compressive Sensing Based Greedy Pursuit Reconstruction Algorithms

In this we are finding minimum energy signal present in the signal. Geometrical solution using l₂ norm as shown in Fig. 14 is blowing up the sphere which is at origin until it touches the hyper plane at some random angle. The point of touch between sphere and hyper plane is smallest energy signal which agrees above equation. That is the best X according to l₂ optimization.

V. Compressive Reconstruction

Y

Ф has nul space of dimension '■n — m¹

M X 1

У1

y2

.ym.

■ Ф 11   Ф 12    Ф 13    Ф 14  ...... Ф i,_n-_m

^Ф 21   ^Ф 2 2   ^Ф 23   ^Ф 24     ^Ф 2,п-т

■^Ф mi   ^Ф m2   ^Ф m3   ^Ф т4 ...... ^Ф m,n-m-

X

[X2

Х3

х4

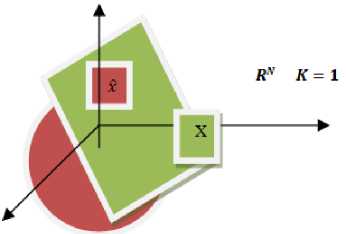
Fig.14. Geometrical Solution Using l2

- xn-

Fig.12. Given Y= x. For which we have to find out x

Reconstruction means for given 'Y' as shown in Fig. 12 (measurements) how to get 'X'. Random projection does not have full rank but we can exploit the fact that we are not interested in acquiring aerial ‘X' , we are interested in acquiring sparse 'x' in CS. For this we are using geometrical structure of sparse signal and Normed vector space. Geometrically null space of is represented using hyper plane of dimension n — m as shown in Fig. 13 which is aligned with coordinate axis with certain angel. All the 'x's such that Фx lives on null space translated to the point 'x'. It means solution is somewhere in the hype plane.

This solution is bad because the sphere and hyper plane touches far away from coordinate axis with random angel so it is not proper signal. Using l₀ minimization (12) reconstruction is improved. Graphically In this method instead of searching minimum energy signal 'x' , we have to search sparsest in the plane.

Optimization x = argmin|x|0          (12)

Since N is million (Mega Pixel) and K is in terms of 10000. This is solved using NP hard algorithm and these algorithm searches all 'K' dimensional subspace to find out sparsest 'X ' . Important factor about these algorithms is that same algorithm can be used to reconstruct the signal irrespective of its basis. Recently some mathematician uses 1 1 minimization (13) for signal reconstruction.

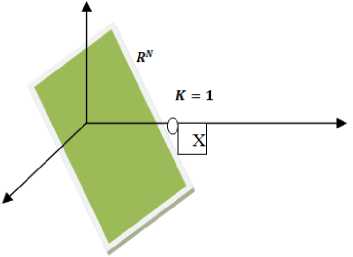
Fig.13. Geometrical structure of Fi of n-m dimensions

Optimization x = argmin|x|1        (13)

But on the hyper plane there are infinite x's present over there. Then search in null space for the best 'x' according to some criteria like least square. Using 1₂ norm which is defined in equation (11) optimize the problem. Optimization (10) means find out the minimum Normed ‘x’ out of all the 'x ' which gives Y = Фx .

Optimization X = argmin||x||2 (10)

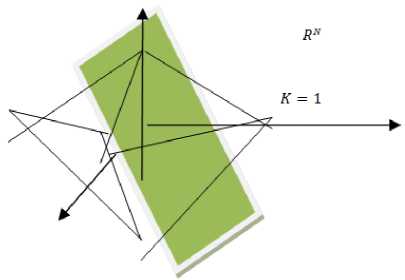
Fig.15. Geometrical Solution Using l0 minimization

Here taking the magnitude of the entire coefficient in the vector and add them will give one sparse signal. Like this we have to repeat for all sub spaces and finally original signal is recovered by using polynomial linear algorithm. Geometrically ( F ig . 15 ) it is as same as L ₂

optimization only difference is we are using pointy structure instead of sphere. This pointy structure may be diamond. When it is blown it pierces at coordinate axis. That point of intersection is the recovered signal.

• V I. Proposed Work and Its Literature Survey

In this work we propose optimized high speed VLSI implementation of Compressive Sensing reconstruction algorithm using FPGA as a prototype.

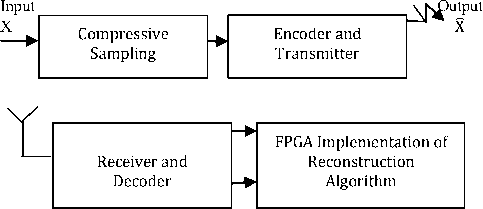
Fig.16. Block Diagram of Proposed Work