A Survey of Artificial Life and Nature-inspired Techniques in Computer Graphics and Visualization

Organically-based models have long been an inspiration for computer graphics techniques which often seek to replicate living creatures and natural phenomena. Some approaches use an image-based technique and operate on a raster grid of numerical values. Others use collections of computational agents which can move independently. But a common aspect is that the rules which govern each pixel, voxel, or agent, are deceptively simple when compared to the complexity of the output. Examples of some of the techniques we will explore in this paper are reaction-diffusion textures, diffusion-limited aggregation, Physarum simulation, boids, multiscale Turing patterns, cellular automata, and differential growth. Some techniques have been active areas of research and spawned many variations. For example, the cellular automata technique has given rise to many recent variatinos, including multiple neighborhoods cellular automata, cyclic cellular automata, and more.

The emergent behavior which characterizes these systems has inspired artists, game developers and those working in other creative fields. By modifying the original, or even just by exposing the parameters of the system to users through a user interface, the power of these techniques may be harnessed for procedural content generation and artistic expression.

In the following section we give an overview of the nature-inspired techniques which are relevant to computer graphics and visualization, and some of the applications that utilize them. Later, the techniques will be compared, contrasted and categorized and the taxonomic relation among them will be described.

2.    Literature Review 2.1.    Reaction-Diffusion Textures and Multiscale Turing Patterns

The reaction-diffusion model of pattern formation was first proposed by Turing [1] to explain such things as the arrangement of arms in a regenerating Hydra and the positioning of leaves around the stems of a Woodruff bush. The analysis presented by Turing was mostly mathematical, describing the conditions for stability and instability in a system of two or more interacting morphogens , the chemicals which govern morphogenesis. The general system of equations governing the concentration of the two morphogens ( u and v ) is:

^ = d u V²u + f(u, v) (1)

^ = d_vV²v + g(u,v) , (2)

where the first term on each right-hand-side is the diffusion term, and d_u , d_v are the diffusion rates of the morphogens, and V² is the Laplacian operator. The reaction functions, f and g , will determine the nature of the patterns generated. Simulation generally starts at a state slightly perturbed from equilibrium. For some parameter values the system may converge to another stable equilibrium. The discretized grid of u or v values can be used along with a color palette to create a color image of the resulting pattern. In the field of biochemistry, many researchers followed with proposed reaction functions which are capable of recreating the patterns on seashells [2], angelfish [3], mammals [4] and snakes [5], and many others.

Witkin and Kass [6] proposed using reaction diffusion to synthesize texture maps for meshes. Whereas previous approaches to solving reaction-diffusion equations used scalar constants for d u and d v , making the diffusion process homogeneous and isotropic, Witkin and Kass' approach used a spatially-varying diffusion tensor (matrix) to make the diffusion process inhomogeneous and anisotropic. Their method numerically solves the equations on a Euclidean domain, but they used the inhomogeneity and anisotropy to avoid texture distortion when applying the texture to the mesh. Turk [7] proposed simulating the process directly on a manifold to avoid the distortion problem.

An example reaction diffusion texture is shown in Fig. 1. This image was generated using the Gray-Scott reaction equations. Different parameter values can give results like stripes, spots and other transient patterns. Substituting different reaction equations gives rise to other families of patterns.

In general the reaction-diffusion equations can also be written as:

^U = div(D_u Vu) + f(u, v) (3)

= div(D_vVv) + g(u, v) , (4)

where div is the divergence operator, D_u, D_v are diffusion tensors which depend on the underlying mesh geometry at each point, and V is the gradient operator, and f and g are reaction functions. The reaction functions can be classified in different ways, depending on how they lead to conditional stability. For example, in activator-inhibitor systems the presence of the activator morphogen causes the production of more of itself and the inhibitor. On the other hand, the inhibitor suppresses creation of the activator. By changing D_u and D_v the spatial scale and orientation of these effects can be modified.

Similar equations to 4 were used by Sanderson et al. [8] to apply reaction-diffusion textures to the problem of vector field visualization. This involves constructing diffusion tensors D_u and D_v at each point such that the diffusion is anisotropic, and the principal diffusion direction is aligned with the vector field at that location. The resulting images feature highly coherent image intensities along streamlines, and more contrast perpendicular to the flow. Reactiondiffusion was also used to simulate the appearance of fruit ring rot [9]. It has also been used as an image processing technique to create artistically stylized images [10], as well as to restore images corrupted by noise and for image superresolution [11, 12].

The diffusion process was generalized even more to become non-Gaussian, governed by higher order tensors [13], to generate more complex patterns, including some with an inorganic appearance. Similar results were obtained by Kim and Lin [14] by allowing the diffusivity function to be an arbitrary function in polar coordinates.

Computational artist, Jonathan McCabe, generated multiscale Turing patterns inspired by reaction-diffusion textures using a single chemical species [15]. Diffusion is performed by local averaging, and the reaction is driven by local concentration differences at various scales. The resulting images have a richer more fractal structure than typical reaction-diffusion textures, as seen in Fig. 2.

Fig. 1. Reaction-diffusion texture example.

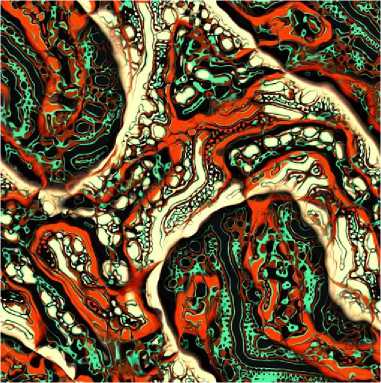
Fig. 2. Multiscale Turing pattern example.

• 2.2.    Diffusion-Limited Aggregation (DLA)

• 2.3.    Physarum

Diffusion-limited aggregation [16] emulates the random walks of diffusing molecules in a 2D or 3D space to generate branching dendritic structures. The process can reproduce the appearance of natural phenomena, such as coral, vasculature, plants and other objects with a branching fractal structure which grow by aggregation [17]. DLA is a possible model for biological self-assembly [18]. In the DLA process, particles move randomly through empty space until they encounter the aggregate structure. The initial structure may be a single particle, or a more complex shape. The aggregation process repeats for a given number of particles, generally thousands or more. An example DLA image is shown in Fig. 3.

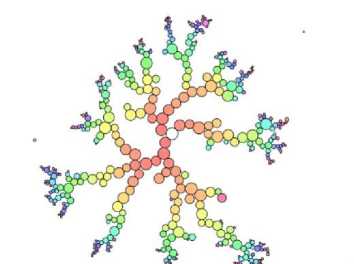
Fig. 3. Diffusion-limited aggregation example.

By incorporating a force field in the random walk, more control over the final form can be taken [19]. This is not a completely artificial concept, since hydrodynamics are known to play a role in coral formation [20]. Bourke [21] described an implementation of DLA in 3D and developed methods for constraining the results to lie within a given mesh. Desbenoit et al. [22] use DLA as the basis for modeling lichen growth on structures to improve the realism of virtual scenes. DLA has also been used as part of a hybrid approach to simulating ice growth [23].

However, while DLA process is adept at generating rudimentary biological phenomena, its capacity to facilitate the formation of intricate shapes might be limited. This limitation can be attributed to the inherent random walk nature of the DLA process, which has the potential to interact with pre-existing structures, thereby influencing the final outcome of the structure's formation. Additionally, the simulation of aggregation growth involves the interaction of a substantial number of particles, reaching into the millions, thereby prompting considerations regarding its viability for resource-intensive real-time applications.

Physarum polycephalum is a member of the myxomycetes class. Though commonly known as slime molds, they are not true fungi, as was once thought, and share some characteristics with protozoa. Physarum polycephalum, specifically, has been an active subject of study due to its complex pathfinding and foraging behavior. Low-level mathematical models of Physarum motion have been developed which allow emergent behavior of the organism to be simulated and visualized.

Physarum polycephalum can often be found in damp forest leaf litter. As it forages for food in organic debris it moves and grows by chemotaxis - movement in response to a chemical stimulus - attracting it toward some substances and repelling it from others. It feeds by surrounding a food source, secreting digestive enzymes, and then absorbing the nutrients. At the microscopic scale, the motion is due to oscillating flow of protoplasm and formation of new branches in the flow network. Agent-based models of the motion have been developed which allow the organism to be simulated.

The structure and behavior of Physarum have been studied for decades [24]. Interest has spanned beyond biology research into computational science and the arts. Physiological properties of the slime mold have been used for sound synthesis and musical composition [25, 26], and it has been the subject photographic and interactive media exhibitions [27, 28].

Physarum has emerged as a model of distributed intelligence that can solve problems, such as shortest path [29], in ways that approximate man-made networks, like the rail system of Tokyo [30]. It solves these problems by flattening out into a thin sheet to explore a wide area, then contracting back into a compact network after a food source is found. Agent-based simulations inspired by Physarum have solved minimum spanning tree [31] and travelling salesman problems [32]. Elek et al. [33] used a stochastic model inspired by Physarum to analyze sparse cosmological data and visualize trajectories between dark matter and galaxies.

Jones [34] modeled Physarum motion in terms of collection agents (representing protoplasm) which can move through an environment, and sense and deposit a chemoattractant into a "trail map". Simulaton results reveal dynamic transport networks which, depending on parameter values, may converge to a stable pattern, or may continue to evolve. Jones performed a systematic analysis of the effect of simulation parameters on the visual appearance of the resulting patterns and explained several of them in terms of low-level physiological processes and high-level slime mold behavior. Jones also experimented with chemorepulsion, making the particles avoid the trail map, resulting in a different family of striped patterns. Some sample Physarum images are shown in Fig. 4.

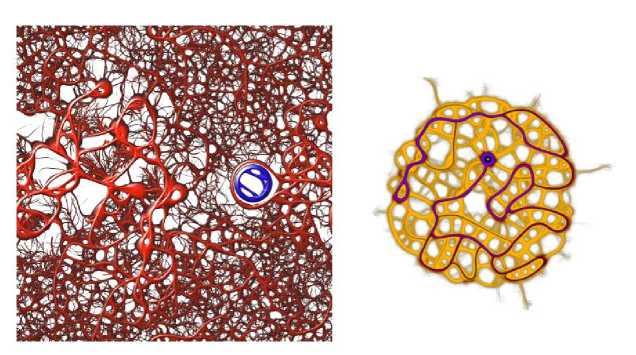
Fig. 4. Physarum.

Jenson [35] described a GPU-based variant of Jones' simulation which was implemented in terms of graphics operations (e.g. point sprites, frame buffer objects). Moving particles representing protoplasm are simulated in a shader and are rendered into a trail map texture which then undergoes additional processing. As demonstrated by Arsiliath [36] the Physarum model can also be implemented as a compute shader. McGraw and Ferdousi [37] extended the Physarum simulation to model multiple species which compete for resources and territory, as a metaphor for social conflict.

• 2.4.    Boids, swarm chemistry

Craig Reynolds' Boids [38] manifest convincing flocking behavior in a collection of agents obeying a few simple rules, and has been the basis for many approaches to realistic crowd simulations in computer graphics applications [39], and even as a visualization technique for the emotional state of crowds [40].

The three rules governing the agents (’boids’) are:

• •    Separation: avoid colliding with nearby boids.

• •    Alignment: keep a velocity similar to nearby boids.

• •    Coherence: stay close to nearby boids.

Each rule can have different distance thresholds for what is considered `nearby', and a weight for the corresponding force. An image sequence from Boids simulation is shown in Fig. 5.

Fig. 5. Boids flocking image sequence.

Hartman and Benes [41] added an additional rule to the original three which gives the flock of boids a leader to follow. This can result in more natural flocking behavior. Moere [42] applied the boids concept to information visualization, as a way of emphasizing how data values change over time.

The rules which define Boids' behavior result in several vector-valued quantities which are summed together to combine their influences. Dodgson and Scott [43] used that as motivation to use Boids to teach vector arithmetic concepts to undergraduate students.

Caporal et al. [44] used Boids in a performance art piece. During the Biodance performance a dancer wears a Virtual reality head-mounted display and holds two motion tracked controllers. The performer can influence the swarming behavior of boids through pose, motion and controller input. The space of curves and strokes generated by Boids, sometimes combined with other techniques, such as genetic programming, has been explored multiple times [45, 46] in the context of computational art pieces. However, the simplicity of the rules governing Boids, when combined with other techniques, can pose challenges to their effectiveness in handling complex scenarios and intricate animations.

Swarm Chemistry [47] is based on similar attraction and repulsion rules as Boids. Additional visual complexity arises from the fact that each agent can have different parameter values governing attraction, repulsion and the interaction radius. The resulting system is animated in an organic way. Sayama also describes evolutionary approaches to designing parameters to achieve desired behavior of the system. Moreover, attaining scalability in Swarm Chemistry can present challenges due to the large agent populations and the diverse individual rules governing these agents. However, simplifying these rules might potentially limit the inherent complexity of real-world swarm behaviors.

In Clusters [48] the agents are grouped into species, and attraction and repulsion rules are determined per species pair. Details of the implementation are not given, but others have tried to replicate the technique and achieved similar results. As suggested by the name, particles tend to clump together into clusters which may be stable or may split and merge in an organic fashion. Clusters are briefly described as implementing a kind of symbiogenesis, an evolutionary theory that mitochodria and chloroplasts in cells originated as independent organisms. It can be seen that mitochodria bear a striking similarity to bacteria and may have descended from cyanobacteria Marguli. The parallel in Clusters is that particles initially moving independently may join together into a persistent symbiotic union.

• 2.5.    Differential Growth (DG)

In certain thin structures, like leaves, flowers and some animal bodies, the rate of growth at edges may be faster than other locations. This leads to a characteristic ruffled or wrinkled appearance seen in kale leaves, carnation flower petals, and sea slugs. Sharon [49] describes the phenomenon in terms of symmetry-breaking and the mechanics of thin-shell structures.

Simulating differential growth requires an initial discretized curve or mesh, values of simulation parameters like stiffness, and a means of collision detection. The mesh grows in a mitosis-like fashion by inserting new vertices and maintaining distances between vertices and their neighbors while avoiding self-collisions with other parts of the evolving structure. An image of Differential Growth in 2D shown in Fig. 6.

The complex organic forms have inspired many computational artists to explore the space of shapes this biomechanical model can generate, both in rendering and fabrication. Andy Lomas incorporated additional rules for nutrient creation based on a process akin to photosynthesis, and transport of the nutrients through the structure [50].

Lomas' simulation continues until the shapes consist of tens of millions of particles. The renderings show a rich natural looking fractal structure. A 3D-printed sculpture of the forms has been displayed in computer art exhibits [51]. The differential growth process was also explored in a series of vase designs and fabrications [52].

Fig. 6. Differential growth of a closed curve in 2D.

Yu [53] developed a web-based interactive tool for designing differential growth shapes which incorporated the influence of gravity. A small user study showed that users were able to understand the connection between mechanical parameters and the resulting shapes and could use the tool as an effective design aid.

Nervous System is a design and fabrication studio which produces works heavily inspired by natural processes. The Floraform project [54] involved the development of tools for interactive design and control of the growth process. As suggested by the name of the project, the resulting animations and fabricated sculptures and jewelry are reminiscent of ruffled flower petals.

• 2.6.    Cellular Automata (CA)

There is a long history of CA, and multiple surveys of the literature have been written [55, 56, 57].The origins of cellular automata lie in von Neumann's research into self-replicating machines. They are closely related to models of computation, like Turing machines. The automaton is a grid of cells which may be in one of a finite number of states. Early work started on 1D grids, but the ideas extend to 2D and 3D grids. Hexagonal grids and other topologies have also been explored. Local rules govern how a cell's state changes based on the states of other cells in a predefined neighborhood.

The first CA seen graphically by many people is Conway's Game of Life, which was originally a model of population. For this 2-dimensional CA, the neighborhood of each cell is defined to be the 8 adjacent cells (the Moore neighborhood). The two possible states for each cell are "alive" and "dead". The three simple state transition rules are:

• •    A living cell with two or three live neighbors remains alive.

• •    A dead cell with three live neighbors becomes alive.

• •    All other live cells die and dead cells remain dead.

The rules are applied simultaneously to all cells in the grid. When visualizing the simulation several interesting characteristic patterns can be seen. Some stable regions emerge. Some periodic patterns, with names like "blinker" and "pulsar", appear. Some moving structures, like the "glider" also can be seen moving throughout the grid. The scale of these patterns is fairly small, just a few cells by a few cells. An example image is shown in Fig. 7.

Fig. 7. Conway’s Game of Life cellular automaton.

Computing the Game of Life on a larger grid just makes those details relatively smaller and harder to see. One variation, called SmoothLife [58], generalizes the game by making the domain and state values continuous rather than discrete. This permits scaling for zooming into smaller structures, and the resulting patterns are smooth instead of blocky, with a more organic amoeba-like appearance. Similar features, such as gliders can also been seen, however, they are able to move smoothly rather than along a discrete set of a few directions.

CA and concepts from evolutionary algorithms have been used for procedurally generating caverns and terrains [59, 60, 61, 62] and indoor dungeon-like levels [63] for videogames .

Moere applied cellular automata to the problem of data clustering [64] to create more comprehensible visualization of complex, high-dimensional datasets. Gobron used per-triangle 2D grids [65] to evolve CAs over triangle meshes. This allows textures to evolve naturally over a surface without distortion. Cracking and peeling surfaces [66] can also be achieved by evolving the CA over a 3D mesh. Tarakanov and Adamatzky used a CA model to determine how clothes drape over virtual characters [67].

The dynamic evolving nature of CA makes it an option for simulating natural phenomena, such as fire, fluids and granular flow. Li et al. [68] use CA to model how fire propagates in underground mines. Boldea [69] used lattice gas CA, a set of particle coupled with the CA grid, for fluid simulations in graphics applications. A GPU implementation of water flow using CAs was described by Topa and Mlocek [70]. A probabilistic CA has been used for modeling granular media in games [71]. This method computed the CA on a custom Margolus neighborhood, an alternating set of 2x2 blocks, for computational efficiency.

Extension of the CA grid and some rules to high dimensions is easy, but the computation time will tend to increase. Gobron described efficient techniques for 3D CA computation on the GPU [72].

Many computational art projects have explored the architectural forms that can be generated by CAs. Krawczyk [73] developed methods to modify the CA output make the results structurally sound, since it is possible that during evolution cells will be generated that have no means of support. Devetakovic [74] extended 2D CAs to 3D by allowing a 2D CA to evolve upwards. She also defined complex smooth NURBS surfaces using CAs.

While Cellular Automata (CA) display considerable potential in generating captivating patterns, they also give rise to scalability concerns when applied to large grids due to their computational demands. The implementation of CA requires complex data structures for rendering. Gobron, for instance, utilized Triangle Strips (TS) and Triangle Fans (TF) rendering structures in CA applications, offering fast and convenient rendering capabilities. Additionally, Tarakanov and Adamatzky addressed the challenge of simulating virtual clothing using an automata network, which boasts faster execution times and minimal CPU and memory requirements. Furthermore, Boldea successfully implemented fluid simulations in both 2D and 3D representations, ranging from lower (20 x 20) to higher (200 x 200) grid resolutions, with incoming molecules from cells geometry.

In the following paragraphs we will give an overview some the many variations of cellular automata that have been proposed.

Multiple Neighbourhood Cellular Automata (MNCA) were proposed by the researcher and computational artist known as Slackermanz [75] on his blog and social media posts. The technique involves using multiple large neighborhoods shaped like concentric rings, which drives up the computational cost of calculation. The sum of live cells in each neighborhood is compared in order to determine state changes. Details of the technique are presented on the Softology blog [76], which also describes the many graphical demos included in the Visions of Chaos tool. MNCA can generate many patterns reminiscent of evolving bacterial colonies. MNCA employs multiple distinct neighborhoods, each with its unique update functions to determine the next-step pixel values. These update functions are continuously evaluated during the execution process, contributing to the computational demands. However, the use of GPU-acceleration can be advantageous in mitigating the computational costs associated with MNCA.

Cyclic Cellular Automata Fisch et al. [77] use modular arithmetic to achieve a "wrap-around" effect in state computation. For example, if a cell can be in n possible states, through n - 1, then incrementing the state n - 1 will result in 0 . Likewise, decrementing 0 wraps to n - 1. Patterns such as repeatedly advancing waves and persistent spirals can be generated. Reiter [78] explored the variety of spirals which emerge from different CCA neighborhoods.

Continuous cellular automata generalize state values to be really valued rather than integer. SmoothLife, mentioned earlier is one such example, but others have been described in the literature. MergeLife [79] is a continuous CA which incorporates another generalization, multiple channels of states. In MergeLife the three channels are directly interpreted as red, green, blue color channels for visualization. Chan describes a system called Lenia [80, 81] which is a continuous CA, and he also catalogued many of the life forms which which may emerge from different configurations of the system. Continuous CA have been applied to image processing problems like edge detection and segmentation [82].

Neural cellular automata (NCA) incorporate characteristics from neural networks into a CA architecture. By replacing the discrete neighborhood logic usually used in CAs with convolution kernels, and incorporating additional hidden layers to implement the CA update rules, a differentiable system is obtained which can be trained using backpropagation techniques. Growing neural cellular automata [83] can generate a small target image, an emoji in the demo code, from a single seed pixel. The resulting pattern is robust to corruption. If a small portion is erased it can regenerate, much like a salamander can generate lost limbs. NCA has also been applied to the problem of image segmentation [84], texture generation from examples [85, 86], generating levels for videogames [87], and generating small voxelized models [88].

• 2.7.    Ant Behavior Simulation

Ants are social species. They work together and live together in highly organized colonies. Ant colonies consist of a queen, workers, and brood(eggs, larvae, pupae). The queen's main role is laying eggs, and young workers take care of the queen and her brood. The older workers' roles are collecting food and protecting the nest from the enemies. Workers have their task preferences, and use communication with nestmates, and environmental cues to decide which task they will perform.

Ants have extraordinary communication skills. They use chemical signals called pheromones to communicate among themselves. 'Danger' pheromones are released in response to enemies to alert nearby ants. 'Food' pheromones create chemical trails from their nest to promising food sources. Ants can smell the pheromones through their antennae and respond to the messages accordingly.

• G. Greenfield and Machado [89] published a survey paper on ant behavior and ant colony-inspired visual art. Examples include paintings based on two types of ants competing for territory and two colonies with 500 simulated ants interacting for 3,000-time steps.

3.    Comparison and contrast of Nature-inspired Graphics Techniques

Pogonomyrmex barbatus (P. barbatus) colony's main food source is seeds. Seeds are a good source of water and fats, which the ants store in their nest for months or several years. The process of seed collection is known as foraging behavior. P. barbatus colonies consist of a queen and three types of workers: nest patrollers, trail patrollers, and foragers.

Nest patrollers leave the nest to assess the foraging area, determine the days of foraging trails and eventually return to the nest. Patrollers also release a chemical within 20 centimeters of the nest to make the direction for trail patrollers. Trail patrollers follow the general direction of nest patrollers and travel around 20 meters until they find a seed and get it back to the nest. Trail patrollers determine the best possible foraging direction from the nest. When both nest patrollers and trail patrollers return to the nest, foragers access their rates of return of seed bearers and decide whether to leave the nest for seeds.

Morehead and Feener Jr [90] has more details about the foraging behavior of P. barbatus. G. Greenfield et al. [91] described ant painting pattern formation based on clockwise seed foraging behavior during patroller trails.

Implementations of ant and ant-colony behavior have used a wide variety of implementations, ranging from CA grid-based techniques [92], to approaches similar to Physarum in that pheromones are deposited into a trail map [93]. The parameters governing ant behaviors in the simulation, including direction, magnitude, pheromone levels, and string length in ant genomes, can be readily calibrated to accurately replicate real-world ant behaviors.

From the previously mentioned biologically-inspired graphics techniques we can see many similarities and common themes emerge. In all cases, individual computational elements interact with other elements and change their state according to some rules, but the identity of the computational elements, and the nature of the communication differ.

Communication and sensing at a distance, three main domains of computation exist in the techniques: pixels or voxels within an image grid, independent particles in a 2D or 3D space, or vertices connected into 2D curves or 3D meshes.

RDT and CA, for example, are image-based techniques which can be computed on 2D or 3D grids. Communication in these systems is simplified due to the regularity of the grid. From any given voxel, neighboring voxels can be directly addressed, though care may be needed near the boundary of the image domain. The values stored in the grid may be discrete, as in CA, or continuous (floating-point) values, as in RDT. Techniques which rely on blurring (Physarum) or, equivalently, diffusion (RDT) propagate information through their domain as a natural consequence of the blurring/diffusion operation. The convolution kernel used in blurring and the discretized differential operators (like Laplacian) used to compute diffusion define the speed at which information can propagate through the domain.

DLA, Boids, and Swarm chemistry work on collections of disconnected points. This requires more computational effort to find neighbors than in image grids. An exhaustive search over all other particles would be prohibitive for large numbers of particles, but spatial hashing, uniform grids or hierarchical data structures like quadtrees and octrees can speed up processing.

Differential growth relies on explicit connectivity between elements, which defines a discrete curve in 2D and a surface in 3D. In DG, immediate neighbors can be found by traversing edges. Spatial search is still useful here to prevent self-intersection by vertices which are not neighbors. In DLA the search for neighbors is the primary activity of the particles. They randomly diffuse through their environment until they find another particle to stick to.

Physarum is an interesting case which is a hybrid of image- and particle-based since the moving agents are points, but they communicate through a trail-map image by rendering into it.

Competing forces , the delicate balance between competing forces can lead to unpredictable behavior when those forces are near equilibrium. Examples of opposing interactions include the activator-inhibitor class of reaction-diffusion systems. In these 2-species models, one morphogen is an activator which increases production of both species, and the inhibitor inhibits creation of the activator. The feedback loop between these two behaviors and resulting instability is a major factor in pattern formation.

In boids, and other particle-based systems there are separation forces which prevent agents from intersecting immediate neighbors, but also coherence forces which encourage large-scale clustering behavior.

In CAs, the rules for state update may have similar nearly-balanced opposition. In Game of Life, for example, living cells with 2 or 3 neighbors stay alive, and dead cells are revived if they have 3 neighbors. Changing these thresholds upsets the delicate balance and results in less stable images.

Regularization , the process of blurring and diffusion in many techniques can be seen as communication technique, but they also serve as a form of regularization. In images, blurring and diffusion can reduce the effect of noise and smooth discontinuities like edges.

This reduces the effect of noise and prevents small disturbances due to noise or instability from propagating. In differential growth there is no blurring or diffusion, but explicit smoothness constraints minimize curvature or length to prevent small discontinuities from being amplified over time.

Turing identified instabilities as a source of pattern formation in reaction-diffusion textures. These instabilities are driven by reaction rules and differing diffusion rates for the two morphogens. The resulting textures are the result of a non-trivial equilibrium state in the system. But, without regularization through diffusion the resulting texture could simply degenerate into noise.

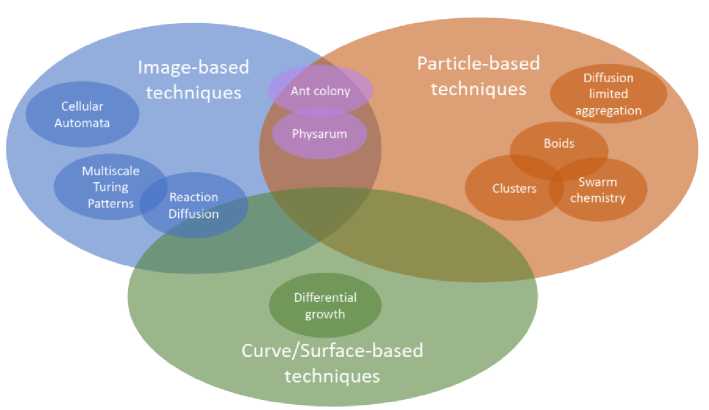
The Table 1 summarizes the comparison and contrast of various biological-inspired graphics techniques. We have also summarized the technique as a concept map to visualize the relationships between the techniques we have discussed. It is shown in figure 8. This representation lets us visualize which techniques are similar to each other and how they relate to the computational domains. For example, reaction-diffusion techniques have been computed on an image domain and directly on mesh surfaces, so RD intersects the overlap on image-based techniques and curve/surface-based techniques. Physarum uses individual protoplasm particles as agents, but those agents communicate through a trailmap image, so it is entirely within the intersection of image-based techniques and particle-based techniques.

Table 1. Comparison of nature-inspired graphics techniques

Techniques	Computational domain	Communication mechanism	Regularization
Reaction-Diffusion Textures (RDT)	Image	Diffusion	Diffusion
Diffusion-Limited Aggregation (DLA)	Particles	Random walk	Blurring
Physarum	Image and Particle	Blurring	Blurring
Boids	Particles	Search	Coherence force
Clusters, Swarm Chemistry	Particle	Search	Local force summation
Multiscale Turing Patterns	Image	Pixel neighborhood	Diffusion
Cellular Automata (CA)	Discrete and continuous images	Pixel neighborhood	None
Differential growth (DG)	Discrete curve and mesh Vertices	Curve and mesh connectivity	Smoothness constraint
Ant colony behavior	Particle	Pheromone trailmap or pixel neighborhood	Various implementation

Physa rum

Boids

Clusters

Curve/Surface based techniques

Reaction Diffusion

Differential growth

Swarm chemistry

Cellular

Automata

Multiscale Turing Patterns

Ant colony

Diffusion limited aggregation

Particle-based techniques

Image-based techniques

Fig. 8. Concept map of artificial-life techniques.

4.    A Taxonomy of Nature-inspired Graphics Techniques

Based on our analysis of the techniques presented here we have developed a taxonomy of artificial life techniques. Figure 9 represents the taxonomy of nature-inspired graphics techniques. This visualization includes more specific variations of techniques, which would have led to excessive clutter in the concept map.

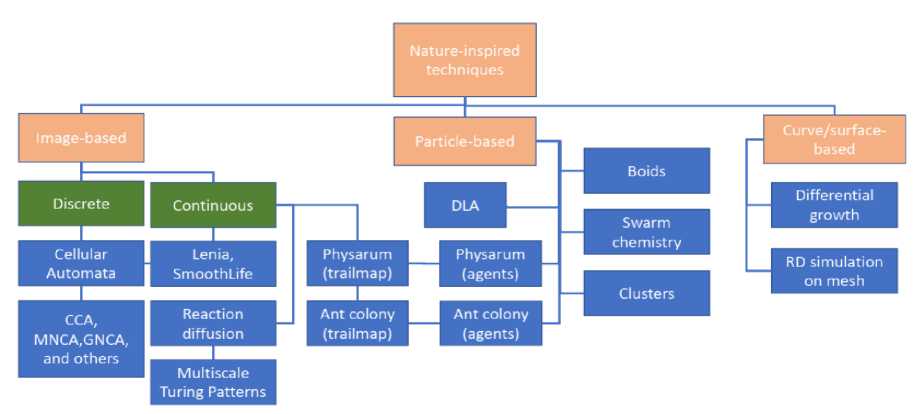
Fig. 9. A Basic Taxonomy for Nature-inspired Graphics Techniques.

5.    Conclusion and Future Work

In this paper we have described and classified many artificial life techniques in the computer graphics literature. We also explored many applications, such as procedural content creation and computational art. Part of the appeal of artificial life in these applications is the property of emergence - that seemingly complex behavior and patterns can arise from simple rules. Simple rules are easily understood and modified by the programmer or artist, giving a flexible, powerful framework within which, the space of images and behaviors can be explored. The process of working with these systems seems to be equal parts creation and discovery.

Although the various techniques may seem unrelated at first glance, there are many underlying similarities which we have described and presented as a taxonomy. What remains unknown are what the minimal set of criteria are for biologically-convincing behavior to emerge from these systems. Understanding the sufficient and necessary conditions would enable development of entirely new techniques. Our hope is that the taxonomy is a starting point for such an investigation.

By comparing and contrasting techniques and finding common themes and patterns it is possible to experiment with variations of existing techniques and hybrids of multiple existing techniques from which new behavior may emerge. Another dimension of these systems which bears further investigation is scale. Real biological systems at the human scale may consist of trillions of cells, but computational techniques at that large scale would lack the interactivity of the systems described here. The patterns and behaviors which emerge from these systems tend to be small. For example, the gliders and walkers which emerge from Conway's game of life are on the order of a few pixels wide, limiting their detail, even when the size of the computational gride increases.

A final open area for continued investigation is how to explore the parameter space of these systems. Artificial life techniques are characterized by a large number of tunable parameters which govern the behavior of the system. Automated techniques for exploring that space and an identifying useful or interesting result would improve the productivity of developers and artists.