A Top-Down Partitional Method for Mutual Subspace Clusters Using K-Medoids Clustering

Published Online September 2017 in MECS DOI: 10.5815/ijieeb.2017.05.06

Subspace clustering is an extension of traditional clustering [1]. It finds set of objects that are homogeneous in subspaces of high-dimensional datasets. Mutual subspace clustering is the process of finding mutual subspace clusters from multiple sources. A single data source is used in subspace clustering whereas in mutual subspace clustering multiple data sources are used.

For example, consider an application of analyzing cancer patients [2]. For this purpose, both clinical data and genomic data have to be collected to develop effective therapies for cancers. Examining clinical data or genomic data individually might not expose the inherent patterns and correlations present in both data sets. Therefore, it is important to integrate clinical and genomic data and mining knowledge from both data sources. Clustering is a powerful tool for uncovering underlying patterns without requiring much prior knowledge about data [3-6]. To determine phenotypes of cancer, subspace clustering has been broadly used to explore such data.

To understand the clusters on clinical attributes well, and to find out the genomic explanations, it is highly appropriate to find clusters which are manifested in subspaces in both the clinical attributes and the genomic attributes. To check whether the cluster is mutual in a clinical subspace and a genomic subspace, the clinical attributes and genomic attributes are used to verify and justify. The mutual clusters are more understandable and interpretable. Mutual subspace clustering is used to integrate multiple sources and mine the related clusters [7].

Consider a data source as a set of points in a clustering space. Let S 1 and S 2 be two clustering spaces formed by subset of attributes. And S 1 ∩S 2 = Φ, and O be a set of points in space S 1 ∪ S 2 on which the clustering analysis is applied. A mutual subspace cluster is a triplet (C, U, V) such that C ⊆ O, U ⊆ S 1 , V ⊆ S 2 and C is a cluster in both U and V respectively. U and V are called the signature subspaces of cluster C in S 1 and S 2 respectively. To make this simple, only two clustering spaces will be considered. However, this model can be easily extended to situations where more than two clustering spaces present.

This paper is organized as follows. Section II discusses the recent developments of the subspace clustering techniques and mutual subspace clustering techniques. The proposed methodology id detailed in section III. The results are analyzed in section IV. The paper is concluded in section V.

• II.    Related Work

Based on the strategy of subspace clustering there are two approaches namely, top-down approach and bottom-up approach [8]. Top-down approach finds an initial clustering in the full dimensional space and evaluates the subspaces of each cluster that iteratively improves the clustering results. The bottom-up approach finds dense regions in low-dimensional spaces and candidate low dimensional clusters are combined them to form clusters in higher dimensional spaces [1]. The redundancy of subspace clusters is eliminated either as post pruning step or in the methodology itself as a wrapper approach.

The top-down methods of locality is determined by some approximation of clustering based on weights for the dimensions obtained so far [9-10]. The algorithms like PROCLUS, ORCLUS, FIND-IT, and δ – clusters determine the weights of instances for each cluster [1114]. The algorithm COSA is unique in that uses the k-nearest neighbors for each instance in the dataset to determine the weights for each dimension for that particular instance [14].

The monotonicity of weak density is used by DUSC (Dimensionality on Biased Subspace Clustering) [15]. DUSC overcomes the problem of density divergence. The density divergence refers to the phenomenon of the data objects being spread farther apart with the increase in the number of dimensions. The process of DUSC is helpful in pruning the search space. Since the density threshold is not same for all the dimensions, the pruning criterion cannot be applied on the search space. The property of monotonicity no more holds. So, if a lower dimensional subspace does not yield any subspace cluster with a specified density threshold, a higher dimensional subspace may yield a subspace cluster with a different threshold [15].

Instead of subspace clusters being generated and then removing the redundant ones, the approach of INSCY (Indexing Subspace Clusters with-in-process-removal of redundancY) finds only subspace clusters which are non-redundant [16]. To accomplish this process a special index called SCY- tree is used to store the regions which are likely to hold subspace clusters. This technique reduces the repeated scanning of database cost for frequent pattern information which in turn stores the whole dataset in the SCY-tree data structure in a compact form with respect to all the projections with one scan of the database only.

Top down k-means method is appropriate where larger mutual subspace clusters exist [7]. That is, in a particular dataset most the points belong to a single mutual subspace cluster. The main goal of mutual subspace clustering is to derive the mutual subspace clusters that supports the multiple data sources. The process of mutual subspace clustering starts with arbitrary k points c 1 …. c k in the clustering space S 1 as the temporary centers of clusters C 1 ……C k respectively. The k centers do not necessarily belong to object set, O.

The data points in O will be assigned to the clusters according to their distances to the centers in space S₁and that point will be assigned to the closest center of the cluster. For each cluster in the subspace the signature subspace is found and the center of each subspace cluster. In this process firstly, we find the signature subspace and the center each subspace cluster in S₂. The Average pair wise distance is used to estimate the signature subspace in S 2 . The Average pair wise distance is used to measure the compactness of the cluster.

This iterative process will be repeated until the clustering gets stable with low miss-assignment rate and the removal of conflict points. Once the conflict points are removed the clustering gets stable and finally the mutual subspace clusters are derived. The algorithm k-means which is sensitive to outliers may substantially distort the distribution of data because of an object with extremely large value [6,8].

• III.    Proposed Methodology

The process of replacing representative objects by non-representative objects will be done iteratively as long as the quality of the resulting clustering is improved. To measure the average dissimilarity between an object and the representative object of its cluster, the quality is estimated by using a cost function. A non-representative object o random is determined which is a good replacement for current representative object o j . The following four cases are examined for each of the non- representative objects, p.

Case 1: p currently belongs to representative object, o j . If o j is replaced by o random as a representative object and p is closest to one of the representative objects, o i, then p is reassigned to o i .

Case 2: p currently belongs to representative object, o j . If o j is replaced by o random as a representative object and p is closest to o random, then p is reassigned to o random.

Case 3: p currently belongs to representative object, o i . If o j is replaced by o random as a representative object and p is still closest to o_i, then the assignment does not change.

Case 4: p currently belongs to representative object, o_i. If o j is replaced by o_random as a representative object and p is closest to o random, then p is reassigned to o random.

A reassignment will be occurred each time, and a difference in absolute error, E will be contributed to the cost function. If a current representative object is replaced by a non-representative object, the cost function is calculated by the difference in absolute error-value. The total cost of swapping is the sum of costs incurred by all non-representative objects. To reduce the actual absolute error E, if the total cost is negative, then o j is replaced or swapped with o random . The current representative object, o j is considered acceptable, if the total cost is positive and cluster members are not changed in the iteration.

• A. Algorithm

Input: a set of points O in clustering spaces S 1 and S 2, the number of clusters k, and parameters θ;

Output: a set of k mutual subspace clusters.

METHOD

END-DO

END-DO

The portion of data points in O which are assigned to different cluster in each iteration has been defined as the miss-assignment rate. The clustering of mutual subspace clusters gets stable when the miss-assignment rate and the signature subspaces of the clusters gets stable. When the signature subspaces of the clustering spaces do not change and the miss-assignment rate will be lower than θ% in two consecutive rounds of refinement, then the iterative refinement stops. Here θ is a user-specified threshold value.

On the other side approximate points might not belong to mutual subspace clusters then the iterative refinement might fall into an infinite loop, subsequently the two clustering spaces does not agree with each other on those points. To identify potential infinite loop, the cluster assignments has been compared in two consecutive rounds of two clustering spaces. The mis-assigned point each which is assigned in different clustering spaces for different clusters, and it is repeatedly assigned to the same clusters in same clustering spaces, then the cluster centers gets stable and the point that does not belong to any mutual cluster is removed. The removed point is named as a conflict point. When these conflict points are removed. Then the centers and the clusters gets stable, thus deriving mutual subspace clusters.

• IV.    Experimental Results

Table 1, 2, 3 and 4 show the corresponding values of execution time for the increased k value when run on different datasets. Figure 2, 3 and 4 shows the performance of the proposed methods in terms of execution time for the other datasets and the corresponding values are tabulated in Table 2, 3 and 4.

"с 60000 з 50000

Е 30000 | 20000 10000

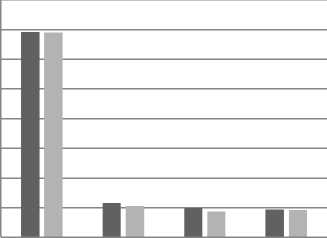
k=2     k=4     k=6     k=8

No. of clusters

Purity is the most common metric used for measuring the quality of the clusters [6,8]. The Purity of a cluster is defined as the ratio of the number of data objects belonging to a maximum class to the total number of its cluster members. In this research work, the subspace clusters with respect to multiple data sources are identified. The purity of a subspace cluster is computed with respect to the signature spaces. The class labels of the abovementioned datasets are compared while computing their purity.

"с 40000 8 35000

Ё 25000 ф 20000 р 15000 10000 5000 0

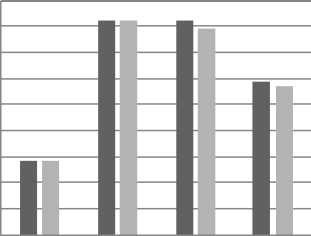
k=2     k=4     k=6     k=8

No. of clusters

Table. 5, 6, 7 and 8 depict the purity of the resulted mutual subspace clusters when run datasets Housing dataset, Wine recognition dataset, Seeds dataset, Column3weka dataset respectively for different values of k. It could be observed that, as the k value increases, the purity of the mutual subspace clusters is improved.

• V. Conclusion

In this research work, a new data mining problem of mining mutual subspace clusters from multiple sources is studied. Most of the real time applications deal with multiple data sources describing the data objects in various contexts. There is a high need for efficient and effective techniques for carrying data analytics in a more meaningful way. This is helpful for the data analysts to make sound decisions.