A Two-Phase Constructive Heuristic for Minimum Energy Broadcasting in Wireless Ad Hoc Networks

Published Online November 2010 in MECS

Wireless ad hoc networks have received significant attention in recent years due to their potential applications in the battlefield, disaster relief operations, and so on. In fact, wireless ad hoc networks are expected to fulfill a critical role in applications in which wired backbone networks are not available, and even economical so as to build for a short temporary usage. Such a network consists of a collection of mobile hosts, which dynamically forming a temporary network without the use of any existing infrastructure [1].

Since there is no preinstalled infrastructure, a communication session is achieved either through a single-hop transmission if the communication parties are close enough or through relaying by intermediate nodes otherwise. The selection of relay nodes is a major issue in routing algorithm design. Another important issue in the routing of ad hoc networks is the energy consumption. In ad hoc networks each node relied on batteries and it may be impossible to recharge or replace batteries during a mission [2]. Therefore, the limited battery lifetime imposes a constraint on the network performance. In order to maximize the network lifetime, the traffic should be routed in such a way that the energy consumption is minimized. Consequently, energy efficiency is an important design consideration for such networks [3].

Broadcast is an important function in applications of ad hoc networks, such as in cooperative operations and group discussions. Broadcasting is an effective means of one to all communication, and is typically implemented by creating a broadcast tree.

Our problem is a source-initiated broadcasting of data in static all-wireless networks. Data is distributed from a source node to each other node in a network. The main objective of this paper is to construct a minimum energy broadcast tree rooted at the source node of a network. Nodes belonging to a broadcast tree can be divided into two categories: relay nodes and leaf nodes. The relay nodes are those that relay data by transmitting it to other nodes (relaying or leaf nodes), while leaf nodes only receive data. Each node can transmit at different power levels and thus reach a different number of neighboring nodes. Given the source node s , we aim to find a set consisting of pairs of relaying nodes and their respective transmission levels so that all nodes in the network receive a message send by s , and the total energy expenditure for this task is minimized. This problem has referred as the minimum energy broadcast (MEB) problem [4]. The problem is proved to be NP-hard [5]. Hence, we use approximation methods as they are generally considered to be the only practical way to solve most real life problems.

In this paper, we propose two new heuristics for the MEB problem based on adaptations of the Fuzzy Greedy Heuristic (FGH) for hard combinatorial optimization problems [6]. The heuristics are named the Fuzzy Greedy Heuristic Broadcast Link-based Minimum Spanning Tree (FGH_BLiMST) and the Fuzzy Greedy Heuristic Broadcast Least-Unicast-cost (FGH_BLU). They consist of two phases: arranging the network nodes in a priority order and then constructing a broadcast tree using the well-known BLiMST and the BLU algorithms. Considering a wide range of instance problems of varying sizes has shown that the FGH_BLiMST and the FGH_BLU give a significantly improved performance relative to the BLiMST and the BLU heuristics, respectively.

The remainder of the paper is organized as follows: in section ΙΙ, the problem definition is outlined. The prior related work is then discussed in section III. Section ΙV belongs to the concept of the fuzzy greedy heuristic and its adaptations. The adaptations consist of two phases: arranging the network nodes in a priority order using the fuzzy greedy evaluation function and then applying the BLiMST or the BLU heuristics. The performance evaluation is outlined in section V. Concluding remarks contain some suggestions for further researches.

• II.    Preliminaries

In wireless ad hoc networks, it is possible to establish a link between any pair of nodes, provided that each has a transceiver available for this purpose. In order to send a message from a node s to a node t , node s needs to emit the message with enough power such that t can receive it. In a model, the power P s required by a node s to transmit data to node t must satisfy the inequality

Ps dist(s,t)a    ^                              (1)

The term dist(s, t) denotes the Euclidean distance between s and t , a >  1 is the distance power gradient, and Y >  1 is the transmission quality parameter. In an ideal environment (i.e. in the empty space) it holds that a = 2 . However, a may vary from 1 to more than 6 depending on the environmental conditions of the network location

In such networks, a power value is assigned to each node. These values, according to (1), determine the range of each node. The range of a node s is the area in which other nodes can receive all messages sent by s .

Using the ranges, one can determine the transmission graph G = (V, E). The vertex set V is the set of nodes, and the edge from s to t is in E if and only if t is within the range of s. All nodes in the range of a node i can receive messages sent by i. The minimal range needed for node i to establish all its out-going connections in G is therefore rG (i) = max dist (i, j).

j ^e N G ( i )

Where N_G(i) denotes the set of out-neighbors of node i in G . The total power needed to establish all connections in G is therefore

c ( G ) = £ Y . r G ( i) ^a . i e V

Since the value of Y does not influence the relative quality of the solutions, we assume Y =1 for the rest of the paper.

Thus, the problem we address involves the designation of which nodes are to be transmited, and the power levels at which they are to do so. Our assumptions are the same as [8] in which the node locations are fixed, and the channel conditions unchanging. We also assume that nodes in a network are equipped with omni-directional antennas. Hence, by a single transmission of a transmitting node, due to the broadcast nature of wireless channels, all nodes that fall in the transmission range of the transmitting node can receive its transmission. This property of wireless media is called Wireless Multicast Advantage, which we refer to this as the WMA [9].

We assume a fixed N -node network with a specified source node, which has to broadcast a message to all other nodes in the network. Any node can be used as a relay node to reach other nodes in the network. All nodes are assumed to have omni-directional antennas. The power matrix of the network, P is an N×N symmetric matrix, in which ( i,j ) ^th element represents the power required for node i to transmit to node j and is given by

• ^P , j = ^di “■ = [ ( x i - x j ) 2 ' I y i - y j ) 2 ] a0 2 , i * ^j . (4)

Where {( x i , y i ): 1 <  i <  N } are the coordinates of the nodes in the network, a is the distance power gradient and d ij is the Euclidean distance between nodes i and j [10].

The shortest-path vector of the network, D is a vector with N elements, in which the i^th element represents the corresponded power of the shortest path from the source node s to node i . It is assumed that an underlying un-icast algorithm (such as the Bellman-Ford or Dijkstra algorithm) provides minimum distance paths from the source node to every other node in the network.

• III.    Related Work

There has been a growing interest in the development of energy-efficient broadcast trees for wireless ad hoc networks. Several energy-aware algorithms have been proposed for the MEB problem. We will now discuss some of those methods that are most relevant to our discussion.

Some works are on the configuration of a network topology with good (or required) connectivity by using minimal power consumption [11], [12], [13], such as minimizing the maximum power of nodes or minimizing the total power consumption of all nodes. Some other works about energy-efficient broadcast are focused on routing protocols, such as in [14], [15], [16]. These routing protocols are distributed routing algorithms that select routes with less energy cost.

Most of the works on energy efficient broadcast are focused on configuring energy power of each node. That is, given the geometry position of a set of nodes in a plane, find the transmitting power of each node such that the energy cost of the broadcast tree is minimized [9], [3], [8], [17], [18]. Wieselthier, Nguyen and Ephremides discussed some fundamental issues associated with energy-efficient broadcast in [9] and several broadcast schemes were proposed and evaluated. They focused on the WMA as the difference between wired and wireless networks. In [3] and [8], they proposed three centralized greedy heuristics to compute an energy-efficient broadcast tree by assigning a range to each node, namely, the Broadcast Least-Unicast-cost (BLU), Broadcast Linkbased MST (BLiMST), and Broadcast Incremental Power (BIP). BLU and BLiMST are link-based approaches which are based on conventional networking technologies. In particular, BLU applies the Dijkstra’s algorithm [19], while the second one constructs a spanning tree with minimum energy according to Prim’s algorithm [20]. BIP is a node-based approach, which is a variant of the Prim’s algorithm by using the WMA property. Wan, Calinescu, Li and Frieder [17] proposed the Broadcast Average Incremental Power (BAIP) as a variation of BIP. The Greedy Perimeter Broadcast Efficiency (GPBE) algorithm in [21] applies the same procedure as BIP, but it is based on another greedy decision metric, defined as the number of newly covered nodes reached per unit transmission power. The Minimum Longest Edge (MLE) and the Minimum Weight Incremental Arborescence (MWIA) are two other heuristics which proposed in [22]. The MLE first computes a minimum spanning tree using as link costs the required transmission powers and then removes redundant transmissions based on the nature of the wireless broadcast. In MWIA, a broadcast tree is constructed using as criterion a weighted cost that combines the residual energy and the transmission power of each node. Optimistic Most Energy Gain (OMEGa) is another heuristic which proposed by Min and Pardalos [23]. In OMEGa, an optimistic energy gain (lower bound or upper bound of lower bound of actual energy gain) of a transmission is used as a measure for transmission selection. With time complexity comparable to that of BIP, OMEGa improves the quality of solutions significantly.

The solutions developed in [3], [8], [9], [17], [18] are mainly based on the geometry features of the nodes in the plane. Some other solutions are based on the graph theory (i.e. based on the connectivity among the nodes in the network), such as in [24], [4], [25].

A heuristic can be further improved by a local search technique. These kinds of techniques can be classified as either tree based or power assignment based. Sweep [9], Iterative Maximum-Branch Minimization (IMBM) [26], Embedded Wireless Multicast Advantage (EWMA) [4], Broadcast Incremental-Decremental Power (BIDP) [27], and Shrinking Overlapped Range (SOR) [28] are some typical examples of tree based algorithms where a tree is updated to a new tree at each improvement step by removing some of the links of the previous one and adding new links. The power assignment based algorithms like r-shrink [29] and Largest Expanding Sweep Search (LESS) [30] make moves based on a new power assignment for each node in the network.

Min [31], investigated three iterated algorithm implementations, IBIP, IOMEGa, ISOR, that are based on BIP, OMEGa, SOR. The algorithms run iterations to find better solutions of the problem. In each iteration, fixing the source node’s transmission power, the algorithm finds the intermediate solutions. And after all the iterations, the algorithm will give the output of the best solution so far. For more details, the interested reader is referred to the excellent survey of Guo and Yang [32].

In [33], we introduced an adaptation of the fuzzy greedy heuristic using the BLiMST. Our focus in this paper is on improving the BLU heuristic using the fuzzy greedy approach devised by Sheibani in [34].

• IV.    The Fuzzy Greedy Heuristic

We aim to improve the BLiMST and the BLU heuristics for the MEB problem using the fuzzy greedy approach. Both two new approaches consist of two phases: arranging the nodes in a priority order and then constructing a broadcast tree similar to the basic heuristics. The priority of the nodes is determined according to the following function

Д ( x ) =

1 + я ff Ь А) x - ₆ ) ² la A ) j

.

In this equation, x is a generic variable associated with the data defining a particular instance of the MEB problem. The parameter θ is a basic measure for evaluating the priority to be assigned to x . The parameter λ is a tuning parameter that is chosen by experimentation such that 0 ≤ λ < 1 to adjust θ .

• A.    The FGH_BLiMST Heuristic

To exploit the fuzzy greedy heuristic idea, we represent x with P i,j as the power required for a transmission from node i to node j . The parameter θ can be assumed as the cost o f the minimum energy broadcast tree obtained by the BLiMST. The steps of the first heuristic are as follows:

• (1)    Calculate μ ( P i,j ) for each element of the power matrix, P .

• (2)    Determine the minimum energy broadcast tree using the BLiMST and select a new node with maximum μ ( P_i, j ) for adding to the broadcast tree under construction.

• (3)    Repeat step 2 until all nodes included in the broadcast tree.

• B.    The FGH_BLU Heuristic

In this case, the adaptation of the fuzzy greedy heuristic is expressed by representing x with d i as the shortest path between the source node s and the destination node i . The parameter θ can be assumed as the cost of the minimum energy broadcast tree obtained by the BLU algorithm. Thus, the basic operations of the second heuristic are described as follows:

• (1)    Calculate μ ( d i ) for each element of the shortest-path vector, D .

• (2)    Determine the minimum energy broadcast tree using the BLU and select a new node with maximum μ ( d i ) for adding to the broadcast tree under construction.

• (3)    Repeat step 2 until all nodes included in the broadcast tree.

It should be noted that in both cases, there are some additional computational efforts independent of N for tuning the parameter λ to obtain the best performance of the heuristics.

Let x min and x max be the smallest and the largest values of x , respectively. We define a small enough value λ min = x _min / ( x _min + θ ) for θ > 0 and any λ ≤ λ _min, for which inequality x ≥ λ min θ / (1 – λ min ) holds. We also define a big enough value λ max = x max / ( x max + θ ) for θ > 0 and any λ ≥ λ max , for which inequality x ≤ λ max θ / (1 – λ max ) holds. It is clear that by setting the parameter θ to zero or setting the parameter λ to a small enough value ( λ ≤ λ min ), µ ( x ) becomes a decreasing function, so that both of the algorithms arrange the nodes by ascending order of the nodes. Whereas, for λ ≥ λ max , µ ( x ) becomes an increasing function and so the heuristics arrange the nodes by descending order of the so-called elements. For more details on the fuzzy greedy evaluation methodology, we refer the interested reader to [35]. The following propositions show that the BLiMST and the BLU heuristics are the special case of our proposed heuristics.

Proposition 1 The FGH_BLiMST heuristic reduces to the BLiMST heuristic if λ is set to a small enough value .

Proof It is obvious that μ ( x ) becomes a decreasing function such that λ ≤ λ _min. Therefore, the FGH_BLiMST heuristic arranges the nodes by ascending order of P i,j . This is equivalent to the BLiMST heuristic.

□ Proposition 2 The FGH_BLU heuristic reduces to the BLU heuristic if λ is set to a small enough value .

Proof It is obvious that μ ( x ) becomes a decreasing function such that λ ≤ λ min . Therefore, the FGH_BLU heuristic arranges the nodes by ascending order of d i . This is equivalent to the BLU heuristic.

□

V.    Performance Evaluation

We performed a simulation study to evaluate our proposed algorithms. The simulations were performed using networks of sizes 20 and 50 nodes on 30 different instances of each size in C++ code. The test problems were taken from (http://dag. . The distance power gradient a assumed to be equal to 2. The performance metric used is the total power of the broadcast tree. For each heuristic, the solution quality is measured by the percentage deviation of the obtained solution from the basic solution (i.e. the BLiMST solution and the BLU solution) through (6).

_      , . c - c' . _ _

Error% =-----x 100.                 (6)

c'

Where c is the minimum transmission power of the obtained broadcast tree using the new heuristics, and c' is the corresponding value obtained by the BLiMST or the BLU heuristic.

• A.    Analysis of Computational Results

We introduced the tuning parameter λ to obtain a good performance of the proposed heuristics. The efficiency of the fuzzy greedy heuristic depends greatly on the choice of the parameter λ in an effective range. If the rang is too small, the probability that it includes the best λ value will be low. If it is too large, the algorithm may waste computational resources and so the waiting time for an improvement could be long. In this experimentation, we evaluate the results obtained for all possible values of λ between λmin and λmax up to 2 decimal places (i.e. with increments of λ equal to 10–2) for each instance.

The simulation of the FGH_BLiMST resulted in different values of X, whose minimum value ( X _mm) varies from 0.0000221 to 0.0027763. The range of the values of λ _max is between 0.6503787 and 0.7702372. In view of the fact that the FGH_BLU was implemented by means of the Dijkstra algorithm, for every instance problem the values of λ min equal to 0 and the values of λ max equal to 0.99. In particular, at each iteration of the Dijkstra algorithm, the elements of the shortest-path vector, D change dynamically; thus, we selected 0, as it is equal to the minimum value of the obtained X m _in at each step. Similarly, 0.99 is corresponded to the maximum value of the obtained X max in every iteration.

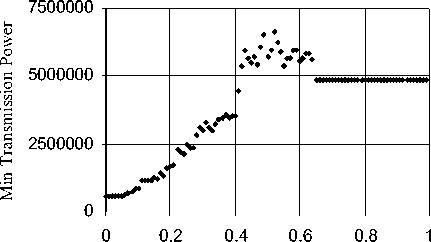
The results show that there exists an effective value of λ between λ min and λ max for which the adaptations of the FGH heuristic yield a good performance that is at least as good as that of the basic heuristics (i.e. the BLiMST or the BLU). Where there are several such λ values, we select the one that corresponds to a minimum transmission power of a broadcast tree, which is closest numerically to the average of these λ values. The selected value is referred as λ *. Fig. 1(a) and Fig. 1(b) exemplify the effect of different values of λ on the computational performance of the proposed heuristics.

The FGH_BLiMST results show that the range of the values of λ * is between 0.00 and 0.06 with the standard deviation 0.01, the average 0.06, the median 0.01, and the mode 0.00.

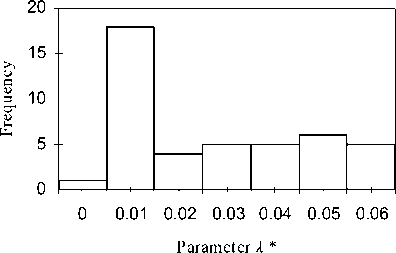
On the other hand, assessing different values of X * obtained by FGH_BLU indicate that they vary from 0.00 to 0.59 with the standard deviation 0.08, the average 0.06, the median 0.04, and the mode 0.01. Fig. 2(a) and Fig. 2(b) show the distribution of the values of λ* as histograms.

In Table I and Table II, the overall performance of the FGH_BLiMST and the FGH_BLU have been reported for different values of λ between λ min and λ max up to two decimal places. According to Sheibani [6], it is expected that the performance of the heuristics with tuning the parameter λ up to four decimal places are sufficiently extensive; however, tuning X up to two decimal places results in a substantial improvement over the basic heuristics.

We recall that, in Table I, the results related to λ min are equivalent to the BLiMST heuristic (by Proposition 1). For every instance, there exists a value of X for which the solution obtained is less than or equal to that of the BLiMST heuristic.

Parameter λ

(a)

(a)

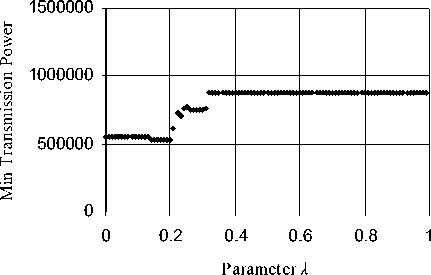
Figure 1. The performance on the instance p20.00 with different values of λ : (a) FGH_BLiMST (b) FGH_BLU .

(b)

In a sense, the FGH_BLiMST can be said to dominate the BLiMST approach. In 43.33% of the instances studied, the minimum transmission power obtained is strictly less than that of the BLiMST heuristic. In addition, on average, 2.20% of all values of λ (up to two decimal places) between λ min and λ max lead to a value of minimum transmission power that is less than or equal to that of the BLiMST heuristic. On average, this adaptation of the FGH heuristic has an error of 0.20% less than that of the BLiMST heuristic.

Similarly, in Table II, it is obvious that the results related to λ _min are equivalent to the BLU heuristic (by Proposition 2). For every instance, there exists a value of λ for which the solution obtained is less than or equal to that of the BLU heuristic. In a sense, this adaptation of the fuzzy greedy heuristic can be said to dominate the BLU approach. In 51.67% of the instances studied, the minimum transmission power obtained is strictly less than that of the BLU heuristic. In addition, on average, 5.03% of all values of λ (up to two decimal places) between λ min and λ max lead to a value of minimum transmission power that is less than or equal to that of the BLU heuristic. On average, this new heuristic has an error of 2.03% less than that of the BLU heuristic.

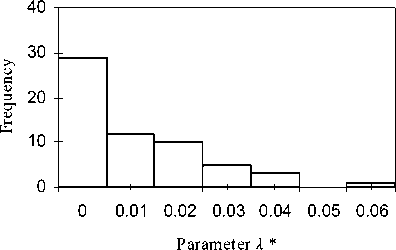
Figure 2. The distribution of λ * as a histogram: (a) FGH_BLiMST (b) FGH_BLU.

(b)

• B.    Computational Complexity

The adaptations of the fuzzy greedy heuristic have the same computational complexity as the basic heuristics. In fact, the FGH_BLiMST and the FGH_BLU have the computational complexity of O ( N³ ) and O ( N ² ), respectively. For the computational experiments discussed in this section, the heuristics were invoked a fixed number of times for any given problem instance. This number, say t , depends on whether we decide to let λ take all possible values to 2, 3 and 4 decimal places over the range from λ min to λ max . The choice of t is then independent of N . Thus, our experimental results have a computational time that is t times that of the BLiMST or the BLU heuristics. In this sense, our approaches are of course more computationally expensive than that of the basic heuristics.

TABLE I.      T he O verall R esults O btained by T he

FGH_BL i MST

Problem size ( nodes )	Problem	Error %
		λ ≤ λ min	λ max ≤ λ	λ *
20	p20.00- 29	0	900.73	– 0.41
50	p50.00- 29	0	1482.61	– 0.003
Average		0	1191.67	– 0.20

TABLE II.     T he O verall R esults O btained by T he FGH_BLU

Problem size ( nodes )	Problem	Error %
		λ ≤ λ min	λ max ≤ λ	λ *
20	p20.00- 29	0	40.48	– 2.30
50	p50.00- 29	0	149.01	– 2.49
Average		0	94.74	– 2.39

However, the theoretical computational complexity of the approaches remains unaffected, since t is a fixed number that is independent of N . We would argue that the additional computational expense incurred by these approaches, compared to the BLiMST or the BLU heuristics, is justified by the significant reduction obtained in the average error.

VI.    Conclusion

In this paper, two new polynomial time heuristics for the minimum energy broadcast problem was proposed. The effectiveness and the efficiency of the proposed heuristics were examined on a set of instance problems of varying sizes. The developed FGH_BLiMST and the FGH_BLU give a significantly improved performance relative to the well-known BLiMST and the BLU heuristics.

For future researches we believe that the following topics are potentially useful: (1) developing efficient adaptations of the proposed heuristics to improve similar approaches for the problem considered, and (2) developing efficient methods using the fuzzy greedy evaluation concept in other areas of combinatorial optimization would be of interest.

Acknowledgment

This research is supported by Iran Telecommunication Research Centre (ITRC) grant number 17570/500. This support is gratefully acknowledged.