A Wavelet Based Approach for Compression of Color Images

Published Online January 2013 in MECS

There are several color spaces to represent a color image, e.g. RGB, HSL, HSV etc. The RGB color model is most popular due to its simplicity. It is well known that the RGB components of color images are highly correlated and if the wavelet transforms of each color component is obtained, the transformed components will also be highly correlated [1][2]. This shows that efficient compression can be achieved using redundancy reduction. Entropy of color image is another important parameter that can be used to characterize the texture of the image. It is important in determining the quality of compressed image, as it decides the maximum codeword length [3]. If image entropy is small, less number of bits are required to represent the image, means more compression can be performed.

Discrete Wavelet Transform (DWT) is a popular technique for image coding applications. In this method the entire image is transformed and compressed as a single data object rather than block to block, allowing for a uniform distribution of compression error across the entire image. DWT has high de-correlation and energy compaction efficiency. The blocking artifacts and mosquito noise are absent in a wavelet based coder due to the overlapping basis functions [4]. Mainly wavelet families can be divided into two parts: orthogonal and biorthogonal. Orthogonal wavelets use the similar filter for reconstruction whereas the length of reconstruction filter differs from the synthesis filter in case of biorthogonal wavelets. The selection of wavelet function is crucial for performance in image compression [5]. Important properties of wavelet functions in image compression applications are compact support, symmetry, orthogonality, regularity and degree of smoothness [6][7].

In our experiment four wavelet families are examined: Daubechies (Db), Biorthogonal (Bior), Coiflet (Coif) and Symlet (Sym). Quality estimation is done on the basis of entropy, PSNR and redundancy. The entropy calculation is done on the basis of color histogram. Section II shows the properties of wavelets, which are important for compression. In section III compression scheme is discussed in detail, in section IV compression quality characterization parameters are discussed. In section V entropy calculation is done from color image histogram. In section VI experimental results are discussed and results are analyzed for various wavelet filters. Finally, in section VII results are concluded and best wavelet filter is finalized.

• II.    WAVELET PROPERTIES

To achieve a high compression rate, it is often necessary to choose the best wavelet filter bank and decomposition level, which will play a crucial role in compressing the images. The selection of wavelet filters plays a crucial part in achieving an effective coding performance, because there is no filter that performs the best for all images [8]. The choice of optimal wavelets has several criteria. The main criteria are [9] [10]:

• 1.    Orthonormality

• 2.    Filter Length

• 3.    Vanishing order or moment

• 4.    Smoothness

• 5.    Decomposition level

• 6.    Regularity

Orthogonal Filters lead to orthogonal wavelet basis functions; therefore the resulting wavelet transform is energy-preserving. The efficiency of a transform depends on how much energy compaction is provided by the transform. Wavelet Filter can be used to analyze or decompose signals and images called decomposition. The same components can be assembled back into the original signal without loss of information, which is called reconstruction or synthesis. Shorter synthesis basis functions are desirable for minimizing distortion that affects the subjective quality of the image. Longer filters are responsible for ringing noise in the reconstructed image at low bit rates [11]. Each wavelet family is parameterized by an integer N called the filter order, which is proportional to the length of the filter. The length of the filter is related to the degree of the smoothness of the wavelet and can affect the coding performance. This relation is different for different wavelet families [12] and non-smoothness basis function introduces artificial discontinuities are reflected as spurious artifacts in the reconstructed images. Higher filter order gives more energy and increases the complexity of calculating the DWT coefficients, while lower order preserves the energy. i.e. it preserves the important edge information. Therefore, we must take care of wavelets in image compression application concerning that good balance between filter orders, degree of smoothness and, computational complexity. These properties depend on the image contents. Vanishing order is the measure of compaction property of the wavelet and it corresponds to the number of zeros in the LL sub band .

Filter Response is another critical property that affects the subjective quality of the reconstructed image. The filter responses approach the ideal rectangular response with the increase in the number of zeros and these numbers of zeros also corresponds to vanishing order of the wavelet. Wavelet Transform can be used to analyze or decompose signal and image called decomposition. The same components can be assembled back into the original signal without loss of information called reconstruction or synthesis. The decomposition process can be iterated with successive approximations being decomposed. However, in practice more than one decomposition level is performed on the image. Successive iterations are performed on approximation coefficients; this successive iterations process yields better energy compaction. The quality of the compressed image depends on the number of decompositions, and these decomposition iterations depend on the filter order. Higher order does not imply better image quality because of the length of wavelet filter. This becomes a limiting factor for decomposition. Usually five levels of decomposition are used in current wavelet based compression [13]. Regularity is one of the properties of the wavelet; greater regularity often does not improve the visual quality.

• III.    COMPRESSION SCHEME

The compression scheme involves three major steps, which are, color space decomposition, wavelet subband decomposition and entropy coding. The first step is to break the color image into different color components represented by RGB color model. These components are forming three different channels. After this stage all the color components are transformed individually. The main purpose of this transformation is to de-correlate the image data and to confine the information into few transform coefficients to achieve the image compression. The second step involves wavelet subband decomposition. Discrete wavelet analysis is computed using the concept of filter banks. Filters of different cutoff frequencies analyze the signal at different scales. Resolution is changed by the filtering and the scale is changed by upsampling and downsampling. The signal is effectively decomposed into two parts, a detailed part (high frequency), and an approximation part (low frequency). The subsignal produced from the low filter will have a highest frequency equal to half that of the original. More specifically this means that upsampling can be used to remove every second sample. The approximation subsignal can then be put through a filter bank, and this is repeated until the required level of decomposition has been reached. The Discrete Wavelet Transformation (DWT) is obtained by collecting together the coefficients of the final approximation subsignal. Overall the filters have the effect of separating out finer and finer details and if all these details are ‘added’ together then the original signals are reproduced. The wavelet transform produces as many coefficients as there are pixels in the image. These coefficients can then be compressed more easily because the information is statistically concentrated in just a few coefficients. This principle is called transform coding [14].

After that, the coefficients are quantized and the quantized values are entropy encoded. Sub-band decomposition has the main advantage of dividing an image into layers with different frequencies. Another property of subband decomposition is that the original image can be reconstructed from the sub-bands with minimum distortion [15]. The first stage subband decomposition is done through the two-dimensional wavelet transform on the image. After the decomposition process, the energy subbands obtained are, Low-Low (LL), Low-High (LH), High-Low (HL) and High-High (HH). The least energy containing the most redundant band is HH band and it is treated as Gaussian noise and therefore is ignored. The LH (lower subband) and HL (higher subband) bands also exhibit the characteristics of a high frequency signal; but there exists correlation among the horizontal and vertical pixels for the former and latter bands, respectively. Although the wavelet transform is an orthogonal decomposition, the visual patterns among coefficients in adjacent subbands hold a striking array of interrelated activity.

Wavelet transform can be applied to both the space and frequency domain. The objective of this step is to produce quantized values, which are directly used by the encoding process. The next stage is the entropy encoding to minimize the coding redundancy. After entropy encoding stage we get three different compressed bit streams for three color channels. The bit streamer combines these three bit streams into a single bit stream and final output is a compressed color image.

IV.COMPRESSION QUALITY CHARACTERIZATION

The compressed image has lost some information in the process of encoding, so some distortion is introduced. The distortion measurement is done by objective quality parameters, which are, PSNR, entropy, redundancy and energy retained. PSNR provides a measurement of the amount of distortion in a signal, with a higher value indicating less distortion. For n-bits per pixel image, PSNR is defined as:

Where, RMSE is the root mean square difference between two images. The PSNR is given in decibel units (Db), which measures the ratio of the peak signal and the error signal (difference between two images).

The fundamental component of image compression is reduction of redundancy and irrelevancy. Redundancy reduction aims at removing duplication from image, and irrelevancy reduction omits parts of the signal that will not be noticed by Human Visual System (HVS). The redundancies in an image can be identified as spatial redundancy,   spectral redundancy and temporal redundancy.   The redundancy measurements in compressed images are done with various filters. Entropy is measured from the 3-D histogram of reconstructed image. The maximum entropy value is achieved when the pixel values are distributed uniformly, and the minimum entropy value is achieved when the image consists of only one level value. In image compression, low image entropy suggests that a high compression ratio can be achieved using efficient coding. The image with lower entropy implies lower image quality for lower information content.

R

PSNR = -0log  - — db                        (1)

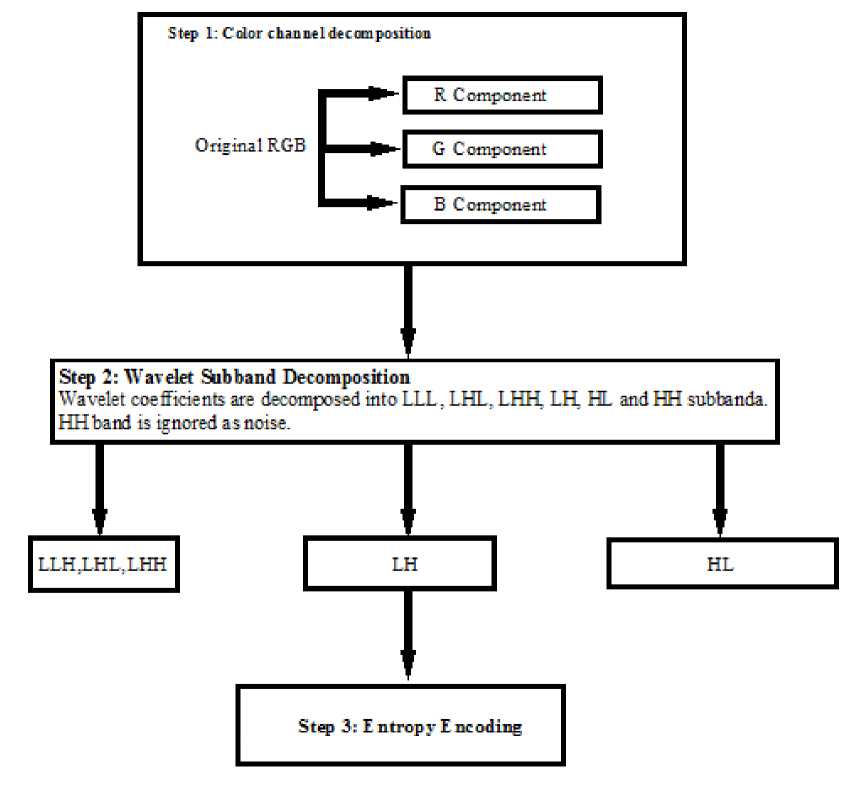
Figure 1: Scheme for color image compression

• V.    ENTROPY CALCULATION THROUGH COLOR HISTOGRAM

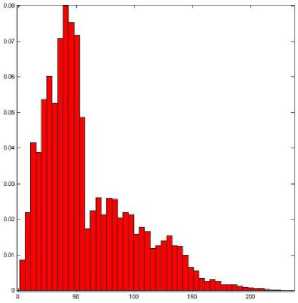
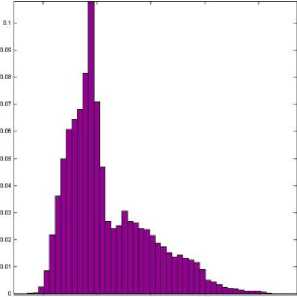
A histogram of an image is measured using 256 bins, which correspond to the 256 quantize levels, and the count of each level is divided by N to give the probability. The maximum entropy value is achieved when the pixel values are distributed uniformly, and the minimum entropy value is achieved when the image consists of only one and the histogram shows one bin. Therefore, the entropy of an image changes with the distribution of the histogram of the image. When an image is natural image, the histogram typically consists of combinational Gaussian distributions in the range (0, 255). In image compression, low image entropy suggests that a high compression ratio can be achieved using efficient coding. The image with lower entropy implies lower image quality for lower information content. In Figures 3 to 6, histograms of uncompressed Zedla test image and compressed image with Db, Sym, Coif and Biortho wavelet filters are shown. The normalized histogram of uncompressed image has more rise and fall; it has a more uniform distribution with more consistent numbers in each bin. And after compression the distribution of pixels become more uniform, which shows that the entropy value is increased and redundancy can be minimized. Entropy values are slightly higher in compression through Biorthogonal filter. Thus more redundancy reduction may be done by using Biorthogonal filter.

• VI.    RESULTS AND DISCUSSION

The wavelet based technique is used to measure the quality of compressed images. The quality estimation parameters are energy retained, entropy and redundancy. The test images used are shown in figure 2. However, experimental results for Zedla image are discussed in detail.

Figure 2: Color test images

TABLE 1: PERFORMANCE EVALUATION OF DB WAVELET FAMILY

Thres hold	Haar			Db4			Db10			Db30			Db40
	PS NR	ER	Red und	PS NR	ER	Red unda	PS NR	ER	Redu ndanc	PS NR	ER	Redu ndan	PS NR	ER	Redun dancy
20	36.6	99.8 4	0.98 9	36.6 1	99.8 8	0.98 9	36. 6	99.9 40	0.98	99. 36.	99.97	0.989 9	36. 7	99. 97	0.989 998
40	31.4	99.6 6	0.98 9	31.5 6	99.7 5	0.98 99	32. 2	99.8 72	0.98	32. 3	99.94	0.989 9	32. 4	99. 94	0.989 995
60	28.5	99.4 8	0.98 9	28.8 3	99.6 3	0.98 99	28. 9	99.7 98	0.989	28. 84	99.90	0.989 9	28. 86	99. 91	0.989 991
80	26.6	99.2 4	0.98 99	27.0 0	99.4 6	0.98	27. 1	99.6 84	0.98	27. 2	99.84	0.989 9	27. 5	99. 85	0.989 985
100	25.1	99.2	0.98	25.6 4	99.4	0.98	25. 7	25.0 3	0.98	25. 72	24.94	0.98	25. 74	23. 60	0.98

TABLE 2: PERFORMANCE EVALUATION OF COIF WAVELET FAMILY

Thres hold	Coif1			Coif2			Coif 4			Coif 5
	PSNR	ER	Redu ndanc	PSNR	ER	Redu ndanc	PSNR	ER	Redu ndanc	PSNR	ER	Redu ndanc
20	36.6	99.89	0.989	36.67	99.92	0.989	36.54	99.94	0.989	36.53	99.95	0.989
40	31.6	99.78	0.989	31.6	99.84	0.98	31.4	99.8	0.98	31.6	99.9	0.989
60	28.9	99.66	0.989	28.9	99.76	0.98	28.7	99.8	0.98	28.6	99.84	0.989

80	27.0	99.5	0.989	27.1	99.64	0.98	26.8	99.7	0.98	99.7	99.76	0.989
100	25.6	99.45	0.98	25.8	99.6	0.98	25.5	99.71	0.98	99.71	99.77	0.989

TABLE 3: PERFORMANCE EVALUATION OF SYM WAVELET FAMILY

Thres hold	Sym2			Sym5			Sym10			Sym30
	PSNR	ER	Redun dancy	PSNR	ER	Redun dancy	PSNR	ER	Redun dancy	PSNR	ER	Redun dancy
20	36.64	99.88	0.989	36.60	99.92	0.98	36.45	99.94	0.989	36.38	99.9	0.989
40	31.62	99.75	0.989	31.56	99.83	0.98	31.33	99.88	0.989	31.21	99.9	0.989
60	28.86	99.63	0.989	28.81	99.75	0.98	28.56	99.82	0.989	28.43	99.8	0.989
80	27.00	99.46	0.989	26.99	99.62	0.98	26.73	99.72	0.989	26.58	99.7	0.989
100	25.63	99.4	0.989	25.65	99.6	0.989	25.39	99.7	0.989	25.23	99.7	0.989

TABLE 4: PERFORMANCE EVALUATION OF BIORTHO WAVELET FAMILY

Thres hold	Biortho1.1			Biortho1.3			Biortho2.4			Biortho2.6
	PSNR	ER	Redund ancy	PSNR	ER	Redund ancy	PSN R	ER	Redun dancy	PSN R	ER	Redund ancy
20	36.6	99.87	0.9899	36.5	99.87	0.98	39.7	99.9	0.98	39.6	99.93	0.98998
40	31.5	99.71	0.9899	31.4	99.71	0.98	34.5	99.8	0.98	34.4	99.85	0.98998
60	28.7	99.56	0.9899	28.5	99.56	0.98	31.7	99.7	0.98	31.5	99.77	0.98997
80	26.8	99.34	0.9899	26.6	99.34	0.98	29.7	99.6	0.98	29.6	99.64	0.98996
100	25.4	99.3	0.989	25.2	99.3	0.989	28.3	99.2	0.989	28.1	99.2	0.98998

О             56            100            150            200

Figure 3: Histogram of original Zedla image

Figure 4: Histogram of Zedla image compressed with Db40

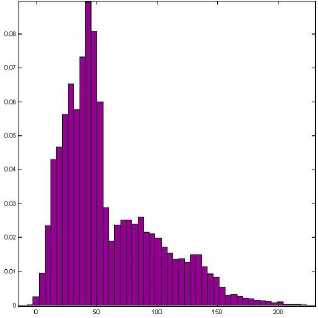
Figure 5: Histogram of Zedla image compressed with Sym30

Figure 6: Histogram of Zedla image compressed with Biortho2.6 filter

• VII.    ANALYSIS OF RESULTS

Results show that the PSNR values are going to decrease as the filter order is increasing within the same wavelet family at same threshold. This shows, although the compression is going to increase with increasing filter length, the compression quality becomes poorer. This is probably due to the process of upsampling and downsampling, as with long filter more zeros are involved in the process, which causes the loss of information and hence the poor quality.

Further, the entropy decreases with increasing threshold, which shows that more compression can be performed. The image entropy value remains unaltered with the increase of filter order; this shows that this is the image property, not the coding algorithm, which affects the entropy values. The redundancy values are decreasing with increasing threshold, which shows the decreasing probability of repetition of neighboring pixels in the compressed image. The effect of filter order is same in both the orthogonal and biorthogonal wavelet families. In both the families redundancy values are decreased with increasing filter order. Redundancy values are 43% higher in orthogonal wavelets as compare to biorthogonal one. All the wavelets do not have the same properties so the compression for different wavelets will have to be different. Orthogonal filters lead to orthogonal wavelet basis functions; hence, the resulting wavelet transform is energy preserving. However, in the case of biorthogonal wavelets, the basis functions are not orthogonal and thus not energy preserving.

Again, the Haar wavelet transform is the simplest one to implement, and it is the fastest. However, because of its discontinuity, it is not optimal to simulate a continuous signal. Based on our experiments, Haar wavelet has obtained the worst compression result, which proves the above statement. Also it is found that visual quality of compressed image deteriorates using longer filters e.g. visual quality of compressed image is superior for Db2 filter as compare to Db40, although it is having higher entropy values.

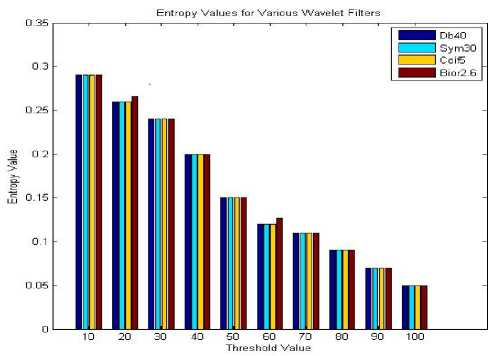
Figure 7: Performance of various filters for entropy calculation

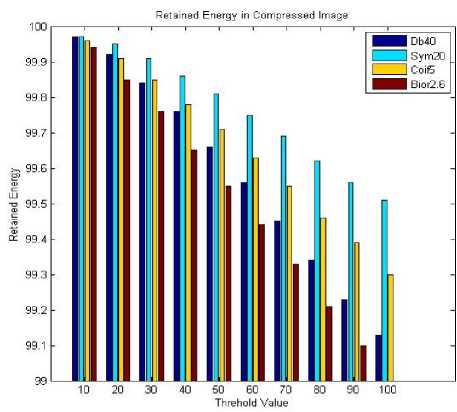
Figure 8: Performance of various wavlet filters for ER

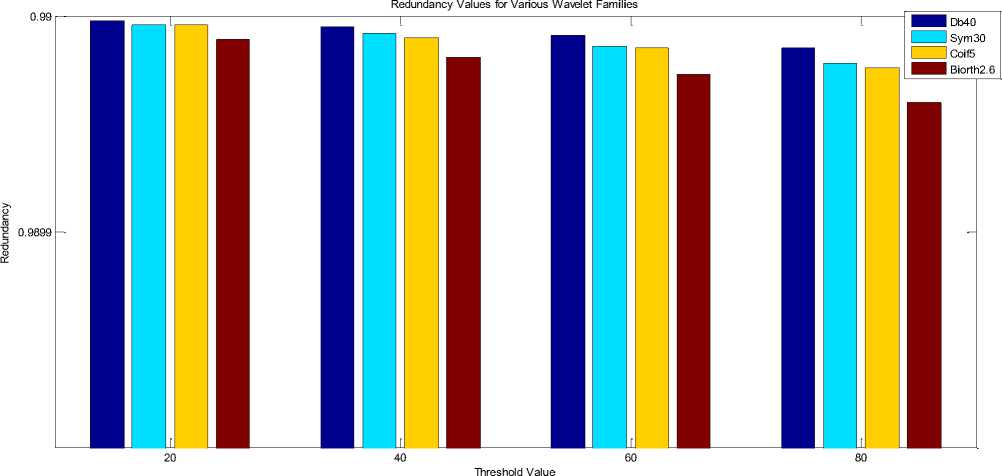
Figure 9: Performance of various wavlet filters for redundancy values

• VIII.    CONCLUSION

In the present work RGB image compression is done by dividing the image into different color channels and compression is performed over each of the channel separately. Proposed scheme is estimated on the bases of ER, entropy and redundancy reduction. Results indicate that better compression can be achieved by using Biorthogonal wavelets whereas orthogonal wavelets are more energy preserving and are having less redundancy. Thus it can be concluded that better compression results can be found if proper wavelet in RGB color space is used depending upon the applications.