Ab initio исследование разогретого плотного аргона

Исследование разогретого плотного вещества представляет большой интерес в физике конденсированного состояния и физике плазмы [1]. Разогретое плотное вещество находится в следующей области параметров: температура 103 — 106 К, плотность 10-1 — 102 г/см3, и давление 101 —104 ГПа. При таких условиях плазма является неидеальной с сильным межчастичным взаимодействием. В природе подобные состояния реализуются в первую очередь в астрофизических объектах, таких как белые и коричневые карлики и газовые гиганты; в лабораторных условиях — с помощью ударных волн, Z-машин, в алмазных наковальнях и разнообразных лазерных установках (см. обзор [2]). Часто исследуются элементы с полностью заполненной электронной оболочкой: водород (дейтерий) [3-5] или благородные газы: гелий [6, 7], неон [7], аргон [8-11], криптон [12], ксенон [7, 10, 13]. В экспериментах обнаруживается высокая проводимость газов (флюидов) при больших давлениях и плотностях,

(с) Сартап Р. А., 2024

• (с) Федеральное государственное автономное образовательное учреждение высшего образования «Московский физико-технический институт (пациопальпый исследовательский университет)», 2024

но и при температурах, заметно ниже энергии ионизации. Возникает вопрос о природе фазового перехода диэлектрик-проводник, или, по-другому, о металлизации.

В случае водорода (дейтерия) фазовый переход с резким ростом проводимости можно рассматривать как близкий к плазменному фазовому переходу [14]. Важная особенность плазменного фазового перехода - то, что он первого рода и имеет скачок плотности. Впервые скачок плотности был получен в разогретом плотном водороде в работе [4], а в работах [15, 16] обнаружена скрытая теплота перехода (см. обзор [17]). Возможность подобного перехода также отмечена и для благородных газов [18]. Однако для них в экспериментах скачок плотности внутри жидкой фазы обнаружен не был, хотя наблюдался рост проводимости на несколько порядков в диапазоне плотностей единиц г/см3.

Методы молекулярной динамики (МД) повторяют результаты экспериментов как минимум на качественном уровне. Из-за необходимости учета квантовых эффектов расчеты проводят в рамках теории функционала плотности (ТФП). Для водорода был воспроизведен скачок плотности [5, 19, 20]; для увеличения точности в [5] использовались интегралы по траекториям. В работе [21] был воспроизведен рост проводимости для гелия, но признаков фазового перехода первого рода обнаружено не было. Вычисления для неона [22] указывают на ионизацию первой и второй электронных оболочек. Моделирование криптона также указывает на переход в проводящее состояние [23].

В работе [11] была получена ударная адиабата аргона на Z-машине и достаточно точно воспроизведена методом квантовой МД. Расчеты проводимости с помощью МД, как и её измерения в эксперименте, в [11] не проводились. В рамках аналитических моделей аргон рассчитывался с помощью химической модели «САХА» в [18] и с использованием модифицированной модели «3+» в [24]; ни в одной из моделей плазменный фазовый переход явно обнаружен не был.

В этой работе методами квантовой молекулярной динамики исследуется разогретый плотный аргон на предмет наличия предполагаемого плазменного фазового перехода. Рассчитано уравнение состояния в области температур Т = 4000 — 25 000 К и плотностей р = 1 — 20 г/см³. Рассчитаны значения электрической проводимости вдоль полученных изотерм, результат сравнивается с существующими аналитическими моделями. Дополнительно произведена оценка параметра неидеальности плазмы.

Электропроводность о(ш) вычислялась как

о(ш) = Е0ШЕ(2^ (ш),

где Eq — диэлектрическая постоянная, е ⁽²⁾ (ш) — мнимая часть диэлектрической функции Е = e ⁽¹⁾ +ze ⁽²⁾. Напрямую из формулы (1) нельзя определить значение статической проводимости од, поскольку наличие частоты ш в сомножителях обращает её в ноль. Для оценки од зависимость ю(ш), полученная по формуле (1), аппроксимировалась формулой Друде о(ш) = o q /(1 + (wt)²) в диапазоне малых ш параметром t.

Мнимая часть диэлектрической функции е ⁽²⁾ (ш) вычислялась по формуле Кубо -Гринвуда [28]:

^Е Т \^w, RI) = 3_m2_w2^ Iqlim   ^  ^2wk [^{f (T}, ^En,k)   f (T,E_n/ ^,k+q)] x

n,n‘,a,k х | (и-п/ ,k |^«

ika\un,k'^\ 5 (En‘,k+q   En,k   ^w) , где T — темпе'ратура. Ri — ионная koiхфпгуратщя. e — 'заряд электрона, m — масса электрона.. Q — объем системы, q — волновой вектор падающего излучения, п. п‘ — электронные состояния, a — пространствен пью координаты, k тонки в зоне брн.ъттоэна Д-сстка). Wk — вес точек в зоне бриллюэна, f (T, E) — распределение Ферми - Дирака, En,k — собственные значения (энергетические уровни) соответствующей волновой функции фп,к в уравнении Кона - Шема. Сама фп,к представляется в виде суммы плоских волн с помощью блоховских функций фп,к = егкгНп,к-

Формула Кубо - Гринвуда (2) включается в себя суммирование по всему спектру частот. Технически спектр дискретен из-за конечного объема расчетной ячейки, и вместо суммы с 5-функцией берется сумма с функцией Гаусса в сомножителях. По умолчанию, в коде VASP ширина функции Гаусса берется равной электронной температуре, устанавливаемой как параметр для распределения Ферми - Дирака. Подобный выбор ширины гауссиана ведет к недооценке проводимости при высоких температурах, где электронная температура достигает порядка единиц эВ [29]. В этой работе ширина функции Гаусса для расчета проводимости предустановлена равной 0.05 эВ.

3.    Результаты

Всего рассчитаны 8 изотерм в области температур T = 4000 — 25 000 К и плотностей р = 1 — 20 г см³. Для ясности на рис. 1 представлена серия изотерм до 12 г см³, начиная только от 8000 К. В случае фазового перехода первого рода ожидалось обнаружить ступеньку на уравнении состояния подобно той, которая обнаруживается при моделировании фазового перехода в разогретом плотном водороде [19, 20]. В разогретом плотном аргоне давление растет плавно с ростом плотности вдоль изотерм, что указывает на отсутствие перехода. Теоретически скачок плотности может быть малым, и имеющийся дискретизации сетки плотность-температура может быть недостаточно, чтобы увидеть излом. Поэтому дополнительно рассчитана одна изохора 6 г/см³ с медленным остыванием, начиная с 14 000 К и заканчивая твердой фазой (рис. 2). Значения температуры и давления на рис. 2 взяты как среднее в промежутке одной пикосекунды моделирования (2000 МД-шагов). Для случая медленного изменения температуры излом также не обнаруживается.

Данные по электропроводности представлены на рис. 3. Изотермы, полученные методом квантовой молекулярной динамики, качественно схожи с полученными с помощью аналитических моделей [18, 24]: есть минимумы, которые сглаживаются с увеличением температуры (см. врезку на рис. 3), хотя положения минимумов отличаются на порядки по как по плотности. При любых моделях изотермы сходятся с увеличением плотности, что можно интерпретировать как переход в металлоподобное состояние. Проводимость разогретого плотного аргона изменяется плавно как с ростом плотности, так и с ростом температуры. Последнее говорит об отсутствии плазменного фазового перехода, так как тот предполагает скачок проводимости.

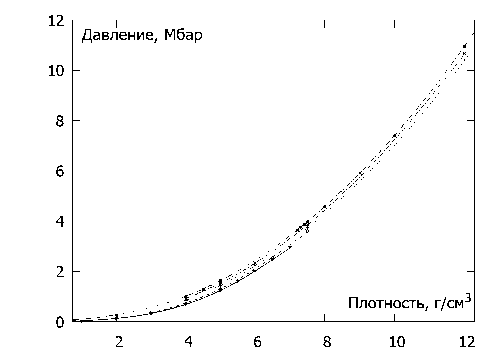
Рис. 1. Уравнение состояния разогретого плотного аргона. Изотермы снизу вверх: 8000 К (сплошная линия с треугольниками), 10 000 К (пунктир с кружками), 15 000 К (пунктир точками с крестами-плюсами), 20 000 К (штрих-пунктир с крестами-иксами), 25 000 К (штрих-пунктир с двумя точками со звездочками). Линии, построенные по точкам, являются аппроксимацией сплайнами

Давление, Мбар

Температура, 103 К

8      9     10     11     12     13     14

Рис. 2. Изохора 6 г/см3 разогретого плотного аргона. Рассчитана путём медленного изменения температуры термостатом Нозе - Гувера. Термодинамические параметры получены рассчитаны как среднее в промежутке одной пикосекунды моделирования (2000 МД-шагов). Пунктирная линия проведена для удобства восприятия

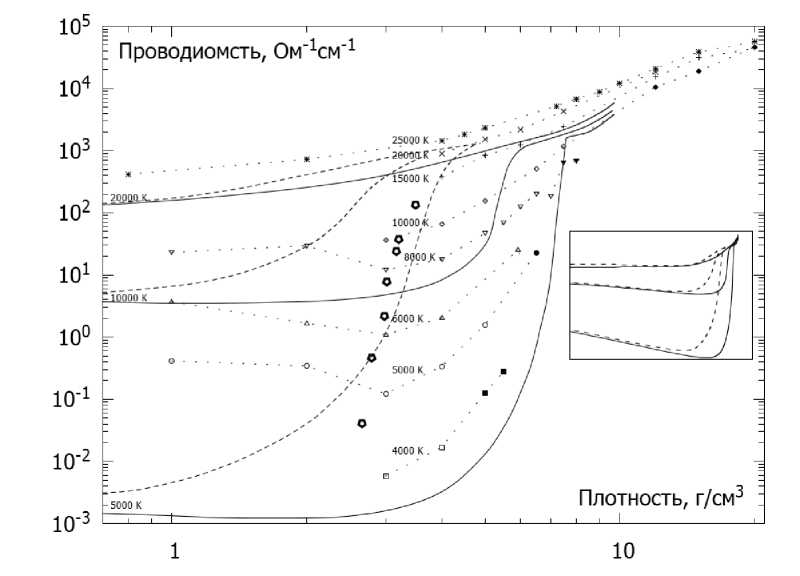
Рис. 3. Электрическая проводимость разогретого плотного аргона. Сплошные линии - изотермы из [18] (химическая модель «САХА»), пунктирные линии - изотермы из [24] (химическая модель «3+»). Точки, соединенные прореженным пунктиром - результат данной работы. Закрашенные квадраты, кружки, треугольники и ромбы - твердая фаза, все остальные точки - жидкая (флюид). Полужирными пятиугольниками обозначены экспериментальные данные [9]. На врезке - результат тех же аналитических работ [18, 24] в тех же координатах, но с увеличенным масштабом по плотности

Результаты МД количественно отличаются от экспериментальных данных [9]. Ударная адиабата [9] (полужирные пятиугольники на рис. 3) получена в диапазоне плотностей р = 2.5 — 3.5 г/см3 и температур Т = 7300-24 400 К. Экспериментальная температура примерно в 2 раза больше, чем предсказывают МД и аналитические модели [18, 24]. Это можно объяснить сложностью определения температуры в эксперименте: измерялась только яркостная температура, а реальная — высчитывалась. Подобное расхождение между МД и экспериментом на ударных волнах можно найти в исследовании дейтерия [30].

В ходе моделирования был получен проводящий твердый аргон (закрашенные точки на рис. 3). Это качественно новый факт, так как использовавшиеся ранее аналитические модели [18, 24] применимы только для жидкости (флюида), а в экспериментах твердый аргон измерялся только при значительно более низких температурах. Расчет этой работы показывает, что электропроводность продолжает расти вдоль изотерм с ростом плотности несмотря на пересечение линии плавления.

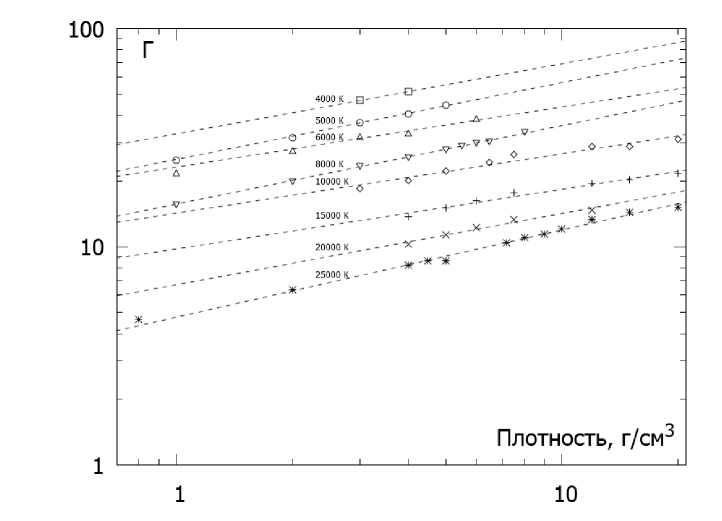
Рис. 4. Параметр неидеалыюсти плазмы Г. Прямые линии проведены как аппроксимация степенной функцией Г(р) = Ар^а

Дополнительно рассчитан параметр неидеальности Г по формуле [31]:

г ^е2      ( ³    У^{1/3 е}2

^Г= т = и "Д  кт                   ⁽³⁾

где е — заряд электрона, к — постоянная Больцмана, Т — температура, г_е — радиус ячейки Вигнера - Зейца, п_е — концентрация свободных электронов.

Для оценки п_е использовалось правило сумм, позволяющее оценить плазменную частоту [32]:

[ “ (2)_М,    "2    ²"2^е2П е

0 ^⁽⁾  d_u =2 _Up =       .

В рамках теории функционала плотности нет разделения на связанные и свободные электроны. Для аргона учитывалось 8 валентных электронов. Оценка п_е ограничивается только внутризонными переходами.

Результаты расчета параметра неидеальности представлены на рис. 4. В исследуемой области плотностей и температур аргон представляет собой сильно неидеальную плазму: параметр неидеальности варьируется от 5 до 50. Эта оценка примерно в два раза больше, чем в [8], где применялась самосогласованная вариационная модель жидкости. В двойном логарифмическом масштабе изотермы ложатся на прямые с примерно одним и тем же наклоном, т.е. Г ~ ра, а = 0.27 — 0.36. По фор муле (3) а и должно быть в районе 0.33 из-за зависимости от концентрации электронов в степени одна треть.

4.    Заключение

Проведено исследование разогретого плотного аргона методами квантовой молекулярной динамики. Воспроизведен рост электропроводности в области температур Т = 4000 — 25 000 К и плотностей р = 1 — 20 г/см³. Результат качественно согласуется с предсказаниями аналитических моделей [18, 24] и с экспериментальными данными [9]. Металлизация происходит плавно с ростом плотности и температуры. Построено уравнение состояния по сериям изотерм; скачков плотности не обнаружено. Признаков плазменного фазового перехода в исследуемой области параметров не обнаружено.

Работа выполнена при финансовой поддержке РФФИ по гранту 20-32-90023 (Аспиранты). Расчеты были выполнены на суперкомпьютерном кластере МСЦ РАН.