Ab initio modeling of Raman and infrared spectra of calcite

The physical properties of the most thermodynamically stable polymorphic phase of the CaCO3 crystal, calcite, have been extensively studied experimentally and can be used to test modern methods of quantummechanical (ab initio) modeling based on the equations of the density functional theory (DFT) [1]. Calcite is widely used in modern optical instruments operating in the infrared and visible wavelengths of electromagnetic radiation. First of all, due to its anisotropic properties, calcite is used in devices of polarization optics. In this paper, we simulate the Raman and infrared (IR) spectra of calcite in an approach based on the semi-classical theory of the Drude–Lorentz scattering, for electromagnetic radiation with a wavelength significantly exceeding the dimensions of the atom [2]. In this approach, the crystal is considered as an ensemble of effective oscillators characterized by a set of natural vibration frequencies and “oscillator forces”. To find the parameters of the model, quantum mechanical methods are used to calculate the spectrum of the elastic vibrations of the crystal and the complex dielectric tensor, which is written in the diagonalized form as the sum of two terms f ν2

^ (^V) = Е-орЩ + Е 2 p 2 p. ----,                   ⁽¹⁾

• ^{ii         opt , ii}     p ν ² _p -ν ² - i νγ _p

where the double index ii defines the direction of polarization, εopt – is the optical (high-frequency) dielectric tensor, νp, fp и γp are the frequencies of the transverse optical oscillations, the oscillator strengths and damping factors for the mode of oscillation p, respectively. The optical dielectric tensor is calculated in the model of quasi-free electrons and the Hartree-Fock or Kohn-Sham approaches [3], as an electron density response to the applied external field, using perturbation theory methods. The calculation of the natural vibration frequencies νp (eigenfrequencies) is performed in the harmonic approximation. For this, the matrix H of the second derivatives of the total energy is calculated from the Cartesian coordinates of the atoms in the relaxed unit cell in which the atoms are in equilibrium. The oscillation frequencies are found as eigenvalues of the Hessian matrix at the Г-point:

( Я²Р )

H r , ь =                      I ^,                         (2)

VMaMb ( duaidubj J where E is the total energy, uαi is the i-th Cartesian coordinate of the α atom.

Methods for calculating Raman and IR spectra, in the above approximation, are described in [4, 5] and are used by us as they are implemented in the CRYSTAL14 software package [6]. In particular, the classical absorption coefficient averaged over the polarization directions is expressed in terms of the imaginary part of the complex refractive index n_i ^* _i ( ν ) = ε _ii ( ν ) :

I (^v) = 3 'EL ^p Im [ n *i ^{( v )} ] .                        ⁽³⁾

Computational Methods

The calculation of the energy of the unit cell of the crystal and all its derivatives in the DFT is performed using all-electronic basis sets of Gaussian type and the hybrid functional B3LYB [6], in the program complex CRYSTAL14 [13]. The choice of this software package is because it has proved to be an effective software product for calculating the structural and frequency properties of ionic crystalline compounds [7]. The choice of the hybrid functional B3LYP, in which the exchange and correlation interactions are described taking into account both the Hartree–Fock exchange and the Kohn–Sham correlation contributions, is due to the large positive experience of its use in calculations of organo-inorganic dielectric structures. In order to take into account the dependence of the calculation results on the choice of the all-electronic basis, we perform calculations with three basic sets: the minimal STO-6G Pople’s base set [8], the basic set with polarization properties – POB-TZVP [9] and the adapted basic set BSD [10]. The first two sets are optimized for the calculation of individual molecules and one-component crystalline structures, respectively. The BSD basic set is a modification of the STO-6G basic set and is optimized for the calculation of compounds containing CO complexes. In the CRYSTAL14 package, the level of accuracy of calculating the energies of the Coulomb and Hartree–Fock exchanges is controlled by a set of TOLIN-TEG parameters, which were chosen as {8, 8, 8, 8, 18}. The accuracy of calculating the self-consistent value of the energy of a unit cell was assumed 10–9 Hartree. The number of basis vectors in the irreducible Brillouin zone is given by the parameter IS = 8, which corresponds to 65 independent k-vectors. The relaxation of cell parameters and atomic positions to equilibrium values was carried out until the effective pressure became less than 0.02 GPa.

Results

The first step is to optimize the geometry of the cell and the position of the atoms for a different choice of basic sets. Table 1 shows the values of the parameters of the crystallographic cell of calcite (hexagonal symmetry group N-167, R 3 C ) for three different basic sets that are compared with the experimental data obtained at T =80 K. The values obtained for the relaxed values of the lattice parameters and c do not differ from the experimental values by more than 1.5 %, which is considered a good approximation. The STO-6G basic set reproduces the calcite crystal density well, but the density values obtained with the other two basic sets are also quite satisfactory.

Table 1. Parameters of a crystalline calcite cell

Basic set	STO-6G	POB-TZVP	BSD	Experiment, [4]
a, Å	5.03	5.06	5.05	4.99
c, Å	16.69	17.32	17.28	17.06
ρ, g/cm3	2.72	2.59	2.61	2.71

The standard test of checking the mechanical stability of a structure is to calculate the matrix of its elastic constants and check for the positivity of its eigenvalues. Table 2 contains the non-zero elastic constants of the CaCO3 crystal, as well as the calculated and experimentally measured values of the modulus of compression (K), the shear modulus (G) and the linear deformation modulus or Young's modulus (E). The elastic moduli are calculated from the values of the elastic constants, as the average of the quantities obtained from the formulas of Reuss and Voigt (Hill's notation) [11]. Also in Table 2 are the calculated values of the Poisson's ratio ν. It can be seen that the basic sets of POB-TZVP and BSD describe the experimental data much better than the minimum set of STO-6G. Another important characteristic of the elastic prop- erties of a crystal is the dispersion spectrum of phonons and the density of states of the phonon spectrum, which are shown in Figure 1, the calculation is performed with a basic set of BSD for the supercell {2, 2, 2}.

Table 2. Non-zero elastic constants of calcite

Constants Cab, and elastic module, GPa	Experiment, [12]	Basic set
		STO-6G	POB-TZVP	BSD
C 11	146.0	208.5	151.7	160.2
C 12	59.7	100.2	53.7	59.3
C 13	50.8	90.4	52.6	55.6
C 14	–20.5	–36.5	–18.3	–17.9
C33	85.0	108.9	81.6	91.6
C 44	34.0	40.5	34.9	36.1
E Н	88.2	85.5	90.2	96.0
G H	32.0	31.1	34.7	36.9
K H	76.8	113.2	74.3	80.3
ν	0.31	0.37	0.30	0.30

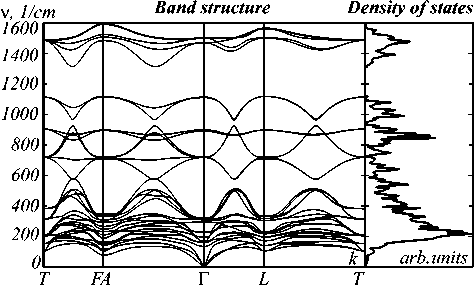
Fig. 1. The phonon spectrum of calcite along the path of high symmetry in the space of the reciprocal lattice

The spectrum observed experimentally at T = 80 K [4] and calculated Raman shifts for different choice of basis sets is collected in Table 3, and the Raman spectrum of calcite is shown in Figure 2. In calculating the complex dielectric tensor ε _ii ( ν ), using the formula (1), the following values of the optical dielectric tensor obtained in the approximation of quasi-free electrons were used: for the base set STO-6G – ε xx = ε yy = 2.43 and ε zz = 1.61; for the basis of POB-TZVP – ε xx = ε yy =2.45 and ε zz = 1.88; for the basis BSD – ε _xx = ε _yy = 2.51 and ε _zz = 1.97. The results of the calculations demonstrate good agreement with experiment when choosing a basic set of BSD, for which the difference between the calculated and experimental values for four frequencies out of five is from 1 to 6 cm^–1. A significant difference (about 35 cm ^–1) is observed only for the highest frequency.

Table 3. Spectrum of Raman frequencies

Raman frequencies	Basic set			Experiment, T=80 K
	STO-6G	POB-TZVP	BSD
ν, cm-1(Eg)	174.0	170.1	158.1	159.0
ν, cm-1(Eg)	394.7	364.2	286.5	286.9
ν, cm-1(Eg)	699.3	669.1	709.8	712.4
ν,cm-1(A1g)	1115.5	917.4	1094.1	1087.1
ν, cm-1(Eg)	1522.5	1167.3	1471.2	1436.6

Intensity 80 V '

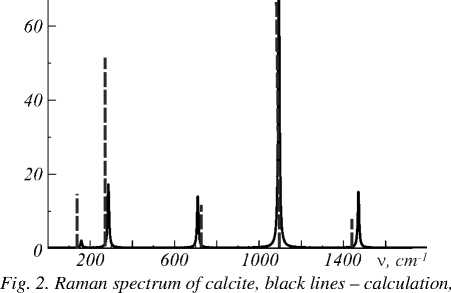
dashed vertical lines – experiment. Intensity is presented in arbitrary units

The Figures 3 and 4 show the results of calculations with the basic set of BSD for the real (n) and imaginary (k) parts of the complex refractive index n ^*, which characterize the scattering and absorption properties of the calcite crystal by electromagnetic radiation in the infrared wavelength range. The refractive index n depends on the polarization of the radiation and the directions of the crystallographic axes of the crystal. In the static limit ( λ→ ∞), its values for mutually perpendicular directions are 2.69 and 2.43 (calculation with the BSD basis), and in the high-frequency (optical) limit – 1.58 and 1.40, which is reasonably consistent with the experimental values for a wavelength of 633 nm – 1.58 and 1.49. Calculations show that the imaginary part of the refractive index k is approximately isotropic and the absorption is independent of the polarization of the IR radiation (see Figure 4) and it is characterized by five narrow absorption bands with significantly different intensities in the range from 6 to 100 µm.

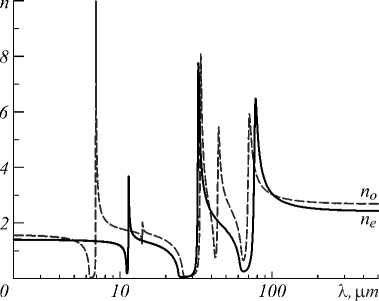
Fig. 3. Calcite refractive index n=Re[n*], as a function of wavelength, for rays parallel to the crystallographic axes a (b) and c of the calcite lattice, respectively

Calcite is a pronounced dielectric with a wide band gap between valence energy levels and the conduction band. Our calculations give the following values for the width of the indirect bandgap: the basis of STO-6G – 5.87 eV, the POB-TZVP basis – 7.62 eV and the BSD basis – 7.69 eV. Thus, the edge of the optical absorption zone begins in the region of the ultraviolet spectrum and the calcite is trans- parent in the visible part of the spectrum and in the region of the peak of standard solar radiation (1.5–3.5 eV).

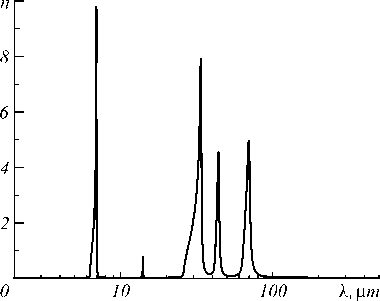
Fig. 4. Coefficient of extinction of calcite k=Im[n*], as a function of wavelength

Conclusion

Modern ab initio methods of quantum mechanical calculations make it possible to describe and make predictions for Raman and infrared spectra of scattering and absorption of electromagnetic radiation of crystal structures. The calculations performed in the CRYSTAL14 software for calcite crystals (CaCO₃) are in good agreement with the available experimental data, which confirms the correctness of the theoretical approach based on the density functional theory [1] and its great predictive capabilities.