Ab initio моделирование энергии растворения азота в ГЦК-решётке железа

Легирование примесями повышает прочность железа, а также влияет на магнитные, электрические и упругие свойства. Обычно легирование осуществляется растворением атомов замещения (хром, марганец, никель [1–3]) или атомов внедрения (углерод, азот [4–5]). Влияние большинства примесей хорошо изучено как экспериментально, так и методами первопринципного моделирования [1–9]. Например, растворённый в матрице азот улучшает стойкость к локальным типам коррозии, что позволяет создавать высокопрочные нержавеющие стали. Несмотря на это работ посвящённых первопринципному моделированию эффектов растворения азота [5] очень мало. В частности отсутствуют расчеты энергии растворения азота в аустените. Попытки моделирования энергии растворения из первых принципов, были предприняты только для ОЦК-железа [6].

Растворение азота в ГЦК-железе представляет собой экзотермическую реакцию (протекает с выделением тепла). Обзор экспериментальных работ проведён в книге [10]. Энтальпия растворения азота в ГЦК-железе составила –0,13 эВ. Но этот результат лишь качественно совпадает с результатами, полученными Фриском при помощи термодинамической оценки с использованием базы данных Calphad [11].

ГЦК-фаза железа стабильна в температурной области, существенно выше точки Нееля, оцениваемой 80 К, и даже выше точки Кюри α-Fe. Её следует рассматривать как парамагнетик с магнитным моментом 0,6µB [12–13]. Моделирование парамагнитного состояния методами зонной теории довольно затруднительно, поэтому возникает вопрос, какая модель его лучше всего описывает. В нашей предыдущей работе [4] моделирование проводилось в немагнитном (НМ) и антиферромагнитном двухслойном состоянии (АФМД), причём АФМД состояние лучше воспроизводило экспериментальные результаты.

Одним из первых получивших, что АФМД состояние является основным для ГЦК-решётки, был Кюблер [7]. В своей работе он ASW методом выполнил расчёты для НМ, АФМД и ферромаг- нитного (ФМ) состояний. В последующих исследованиях Херпера [8] и Медведевой [9], в которых к рассмотрению было добавлено антиферромагнитное однослойное состояние, также было получено, что АФМД состояние является наиболее стабильным из коллинеарных магнитных структур ГЦК-железа. Моделирование в НМ состоянии менее ресурсоёмкое, в отличие от других состояний, поэтому его удобно использовать для качественных оценок.

Таким образом, проведя анализ работ, мы пришли к выводу, что целесообразно рассмотреть: энергию растворения, влияние азота на геометрические параметры системы после его растворения, а также отделить упругий вклад от растворения азота от химического. Следовательно, целью данной работы являлось ab initio моделирование энергии растворения азота в различных магнитных фазах ГЦК-железа, с помощью программного пакета WIEN2k [14]. Как и в нашей предыдущей работе [4], моделирование проводилось в двух различных магнитных состояниях ГЦК-железа: НМ и АФМД состоянии.

Методика

В данной работе расчёты проводись из первых принципов полнопотенциальным методом FLAPW [15], с учетом обобщенного градиентного приближения PBE-GGA [16] в программном пакете WIEN2k, обеспечивающим высокую точность расчета полной энергии при минимальном количестве подгоночных параметров.

В нашей работе использована ГЦК-супер-ячейка, состоящая из 32 атомов с параметрами R mt (Fe)=2,0 а.е., K max =5 а.е.^–1. Для определения геометрических параметров необходимо использование N k = 64 точки в схеме Монхорста – Пака[17], а чтобы гарантировать точность вычисления полной энергии в 1 мРб, необходимо его увеличить до N_k = 343. Обсуждение параметров моделирования было проведено нами в работе [4].

Энергия растворения азота определялась формулой

A H = E ( Fe 32 N ) - E ( Fe 32 ) - 2 E (^ _g ) ) ,

Энтальпия диссоциации молекулы азота

Таблица 1

Работа	Значение энергии, эВ
Да нн ая ра бот а	10,5
[18]	9,867
[19]	10,558
Эксп. [20]	9,8

Таблица 2

Параметры решётки ГЦК железа до и после растворения азота

Суперячейка НМ, Å АФМД, Å Эксп. [21], Å Fe32 3,45 3,54 3,534 Fe32N (3 ат. % N) 3,475 3,56 3,574 где E (Fe32N) - энергия отрелаксированной супер-ячейки, состоящей из 32 атомов железа и 1 атома углерода, находящегося в октапоре; E (Fe32) - энергия суперячейки, состоящей из 32 атомов железа; E (N2(g)) - энергия молекулы газообразного азота.

А т ом а з о т а при ра с творе н и и упру го ра с т ал кивае т бли ж а йш ие а т ом ы желез а , а т а кже в с ту па ет в химическое в за им од ей с тви е с а т ома м и же л ез а . Упруго е и хим иче ско е в з а и м оде йс тв ие м ожно вычислить, используя формулы:

^E уп р = E ( ^N ) нер - E ( F e 3 2^N ) ;

Eхим = E (Fe32N)нер - E (Fe32N) — 2 E (N2(g) ), где E (Fe32N )нер - энергия нерелаксированной суперячейки, состоящей из 32 атомов железа и 1 атома азота.

М ол е к у л а а з ота м одел иро в а л а с ь в кубе со сте нк а ми 15 а . е . При инте г рирова ни и в обра тном прост ра нс тв е , для дос т ижени я н еоб ход им ой т очности было достаточно 1 k -т очки в ЗБ [18–19]. Для пров е рки т очнос ти на ше й м оде л и произ в ед ен о сра в не н ие эн т ал ь пи и д ис социа ц и и со значением э н тал ь пи и в ра бо т ах друг их ав т оров (т а бл . 1). Из-за перекрытия маффин- т и н рад и у с ов в м о л е куле азота, нам пришлось взять R_mt ( N) = 1,0 а.е.

Из табл. 1 видно , что н аш р езу л ь т а т о тли чается от экспериментального на 7 % [20] , н о сов п адает с резу л ьт а т а м и по лу че н н ым и в ра бо те из пе рв ы х принципов [19] , чт о поз во л яе т говорить о дос т оверности расчетов.

Результаты расчета энергии растворения азота

При растворении одиночного атома N в су-перячейке НМ ГЦК-железа увеличивается параметр решётки с 3,45 до 3,475 Å и атом азота расталкивает ближайшие атомы железа на 6,6 %. При растворении азота в АФМД состоянии происходит увеличение параметра решётки с 3,54 до 3,56 Å (табл. 2) и образование в первом окружении слегка искажённого октаэдра, у которого магнитные моменты апикальных атомов выстраиваются в одном направлении, т. е. происходит переворот спинов (см. рисунок). При этом планарные атомы смещаются на 6,6 % и имеют магнитный момент 1,46 µB, а апикальные: один поменявший направление спина смещается на 3,4% и имеет магнитный момент 0,3µB, другой атом с магнитным моментом 2,08µB смещается на 5,1 %.

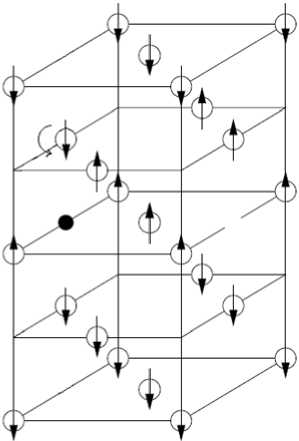
Результат растворения атома азота в решётке ГЦК-железа в АФМД состоянии

Сравнение энергии растворения азота проведено в табл. 3.

Из табл. 3 видно, что значение энергии растворения азота согласно АФМД расчёту, ближе к экспериментальному значению, чем в НМ, как и в ранней нашей работе [4]. Тем не менее, при использовании АФМД магнитной структуры возникает проблема. Нарушается магнитное состояние ячейки. Из-за переориентации спинов атомов железа в ближнем окружении атома азота ячейка приобретает отличный от нуля магнитный момент, что отличается от реального состояния парамагнитного ГЦК-железа.

Упругий и химический вклады в энергию растворения азота представлены в табл. 4.

Таблица 3

Энергия растворения азота в ГЦК Fe

Работа	Энергия, эВ
Данная работа, АФМД	–0,27±0,02
Данная работа, НМ	–0,42±0,02
Эксп. [10]	–0,13±0,005
[11]	–0,53

Таблица 4

Упругий и химические вклады в энергию растворения азота

Магнитное состояние	Упругий вклад, эВ	Химический вклад, эВ
НМ	1,47	1,08
АФМД	1,35	1,05

Из табл. 4 видно, что при растворении азота упругий вклад больше, чем химический. Химический вклад почти не зависит от того, в каком магнитном состоянии проводилось моделирование.

Заключение

Таким образом, в результате проведенных исследований:

• 1.    Впервые из первых принципов была вычислена энергия растворения азота в ГЦК-железе, а также разделён упругий и химический вклад в неё. Получено, что упругий вклад при растворении азота больше химического.

• 2.    Показано, что при растворении одиночного атома N в ГЦК-железе увеличивается параметр решётки с 3,45 до 3,475 Å и атом азота раздвигает ближайшие атомы железа на 6,6 %. При растворении азота в АФМД состоянии происходит увеличение параметра решётки с 3,54 до 3,56 Å и образование в первом окружении слегка несимметричного октаэдра, у которого спины апикальных атомов выстраиваются в одном направлении.