Ab initio моделирование межфазной границы феррит/цементит

Хорошо известно, что растворимость углерода в низкотемпературной полиморфной ОЦК-модификации железа очень низка, так что практически весь углерод в промышленных сплавах железа (сталях), как правило, содержащих от 0,5 до 5 ат. % С, присутствует в виде карбида железа Fe 3 C (цементита), существующего совместно с почти чистым α -желе-зом (ферритом). В медленно охлажденных сталях цементит является частью структурной составляющей, называемой перлит, представляющей собой смесь тонких пластин феррита и цементита [1]. Среднее расстояние между пластинками перлита, который образуется изотермически из аустенита, зависит от температуры превращения и существенно влияет на твердость и прочность сталей [2].

Среди множества причин, объясняющих пристальное внимание специалистов к структуре перлита, можно выделить то, что из сталей с такой структурой изготавливается большое количество изделий (канаты, высокопрочная проволока, рельсы, заготовки для волочения, арматура и др.), в которых перлит в значительной степени определяет важнейшие механические свойства, а следовательно, надежность и долговечность конструкций. Кроме того, перлит представляет собой уникальную сложную структуру, которая может быть воспроизведена во многих модификациях [3, 4].

Межфазные границы феррит/цементит также играют важную роль в процессах адсорбции примесей (например, водорода) в стали. В частности, хорошо известно [5], что в поковках многих инструментальных сталей (штамповых, быстрорежущих и др.) практически никогда не наблюдаются флокены, хотя содержание водорода в них может достигать достаточно больших значений. Поскольку карбиды не растворяют водород [6], то высказывалось предположение о захвате водорода в ловушку межфазными границами α -твёрдого раствора с карбидами железа, хрома, титана и др. [6–9].

Помимо экспериментальных методов исследования для количественного анализа взаимодействия примесей с дефектами решётки используют методы компьютерного моделирования [10–12]. Данные методы позволяют построить структурную модель самих дефектов, оценить их энергетические и магнитные характеристики, а также провести

Физическая химия и физика металлургических систем

исследования взаимодействия дефектов с примесями. Настоящая работа посвящена моделированию межфазной границы феррит/це-ментит: определению оптимальных параметров моделирования и оценке характеристик границы.

Построение структурной модели межфазной границы феррит/цементит

Цементит Fe3C имеет орторомбическую решетку, принадлежащую к пространственной группе Pnma. Элементарная ячейка с параметрами a = 4,524; b = 5,088; c = 6,741 Å [13] содержит 12 атомов железа и 4 атома углерода. Структура цементита состоит из плоских слоев трехгранных призм, образованных ато- мами железа, которые параллельны плоскости (001). Внутри каждой призмы находится атом углерода. Имеется два типа кристаллографически неэквивалентных слоёв атомов железа, находящихся в позициях, обозначаемых G

(general) [14]:

± [[ x , y , z ]];

± [[1/2- x , 1/2+ y , z ]];

± [[ x , y , 1/2- z ]];

± [[1/2- x , 1/2+ y , 1/2- z ]]

и S (special):

± [[ u , v , 1/4]];

± [[1/2- u , 1/2 + v , 1/4]].

Атомы углерода при

расположении в

центрах «нормальных» призм имеют координаты [15]:

± [[ r , ^ , 1/4]];

± [[1/2- r , 1/2 + 5 , 1/4]].

Согласно [16] параметры равны:

x = 0,333; y = 0,175; z = 0,065;

u = –0,167; v = 0,040; r = 0,43; s = –0,13.

Разные пластины каждой из фаз в пределах одной колонии перлита имеют единую кристаллографическую ориентировку, а взаимная ориентировка двух фаз обеспечивает наилучшее сопряжение их кристаллических решеток по габитусной поверхности пластин [17]. Для сопряжения решеток известны три типа ориентационных соотношений (ОС): Багаряцкого с габитусной плоскостью (001) ц || (112) ф , Исайчева (101) ц || (112) ф и Петча–Питча (001) ц || (125) ф [17, 18]. Соотношения Багаряцкого и Исайче-ва очень близки и имеют разориентировку всего в 4° [17]. Для перлита, образующегося при небольших переохлаждениях ниже критической точки, доля колоний с ОС Исайчева и Петча –Питча примерно одинакова, но с понижением температуры превращения вероятность реализации ОС Исайчева повышается [19]. Поэтому для дальнейшего исследования было выбрано именно ОС Исайчева.

Габитусные плоскости (101) в железной подрешетке цементита образуют двенадцатислойную укладку со средним межплоскостным расстоянием V a ² + c ² /12 = 0,677 А, причем можно выделить плоскости двух типов, содержащие атомы железа в G - и S -позициях, расположение атомов в которых несколько различается (рис. 1). Наиболее вероятно, что плоскости (101) ц , образующие когерентную межфазную границу, будут содержать S -атомы, во-первых, поскольку укладка атомов в

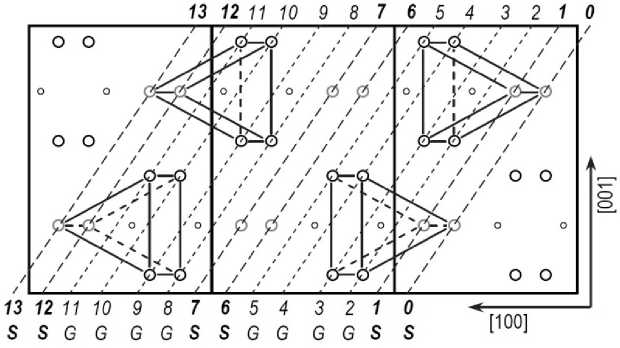
Рис. 1. Проекция решетки цементита вдоль направления [010]. Пунктиром показаны плоскости (101). Атомы железа в позициях S изображены светлее; кружочки меньшего размера – атомы углерода в центрах «нормальных» трехгранных призм

таких плоскостях гораздо ближе к плоскости (112) α , а во-вторых, поскольку при этом не нарушается целостность образующих решетку цементита трехгранных призм, внутри которых находятся атомы углерода.

Для построения структурной модели данной межфазной границы, пригодной для перво-принципного моделирования, необходимо сконструировать суперячейку, позволяющую ввести периодические граничные условия. Для того, чтобы обеспечить целостность поверхности раздела при данных граничных условиях, межфазная граница должна быть параллельна одной из граней суперячейки. В нашем случае система координат должна быть изменена таким образом, чтобы габитусная плоскость (101)ц || (112)ф была параллельна одной из координатных плоскостей. Супер-ячейка должна состоять из двух частей: це-ментитной и ферритной, содержащих достаточное количество атомных плоскостей для того, чтобы взаимодействие соседних границ раздела было незначительным. Подробно процесс построения такой суперячейки описан в работе [20]. Выбранная суперячейка содержит 64 атома: 56 атомов железа (по 28 в цементитной и ферритной частях) и 8 атомов углерода (рис. 2, а). Для удобства моделирования моноклинная суперячейка с углами α = γ = 90°, β = 67,73° была преобразована таким образом, чтобы стать ближе к орторомбической (α = 94,221°, β = γ = 90°) при сохранении слоистости структуры и количества атомов на границе (рис. 2, б).

Определение параметров моделирования

Расчет электронной структуры был проведен полнопотенциальным методом линеаризованных присоединенных плоских волн (FLAPW) с учетом обобщенного градиентного приближения (GGA) в программном пакете WIEN2k. В методе FLAPW волновые функции, зарядовая плотность и потенциал разлагаются по сферическим гармоникам в непере-крывающихся атомных сферах радиуса R mt и по плоским волнам в остальной области элементарной ячейки. Предполагается, что внутри muffin-tin сферы зарядовая плотность сфе-рически-симметрична. Волновые функции в междоузлии раскладываются по плоским волнам с вектором обрезания K max . Эта величина является одним из основных параметров, влияющих на точность, так как она определяет

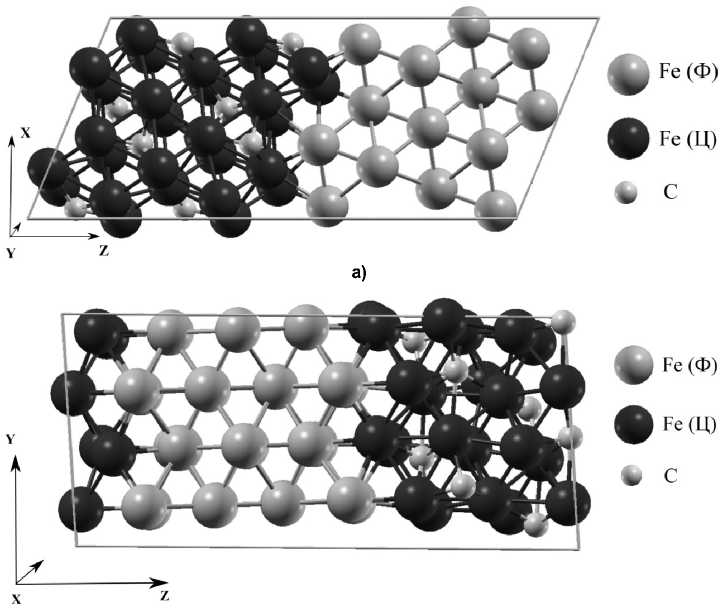
б)

Рис. 2. Структура суперячейки с межфазной границей феррит/цементит: а – при α = γ = 90°, β = 67,73°; б – при α = 94,221°, β = γ = 90°. Ф – феррит, Ц – цементит

Физическая химия и физика металлургических систем

число базисных функций (размер матриц). Еще одним немаловажным параметром является количество k -точек. Эта величина характеризует дискретную сетку, используемую для численного интегрирования по зоне Бриллюэна.

В первую очередь была выполнена оптимизация количества k-точек, так как этот параметр не зависит от других. Были взяты зна- чения:

a =5,088; b =8,118; c =16,842 Å;

α =94,221°, β = γ =90°;

R mt (Fe)=2,0 a.e.; R mt (C)=1,4 a.e.;

E cutoff =–7,0 Рб (340 эВ), K max =5,0 а.е.^-1.

На рис. 3 представлен график зависимости энергии системы от количества k-точек. (Здесь и далее для каждого параметра моделирования указывается относительная энергия, равная разнице между энергией системы и ее ми-мальным значением для данного параметра.)

Как видно из рис. 3, увеличение k -точек выше 64 не приводит к значительному изменению величины полной энергии (в пределах 0,01 эВ), следовательно, оптимальным значением количества k -точек является 64.

При данных параметрах проведена серия расчетов, позволяющая определить постоянные решетки равновесной структуры межфазной границы феррит/цементит. Для этого сначала варьировался объем системы при постоянных значениях параметра решетки c и отношении a/b (вместе с объемом менялся и угол α) (рис. 4).

Из рис. 4 видно, что для двух значений объема (679,924 и 686,862 Å3) энергия систе-

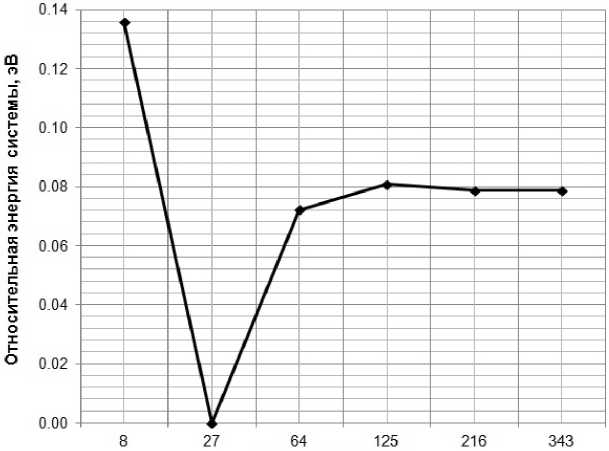
Количество к-точек

Рис. 3. Зависимость энергии системы от количества k -точек

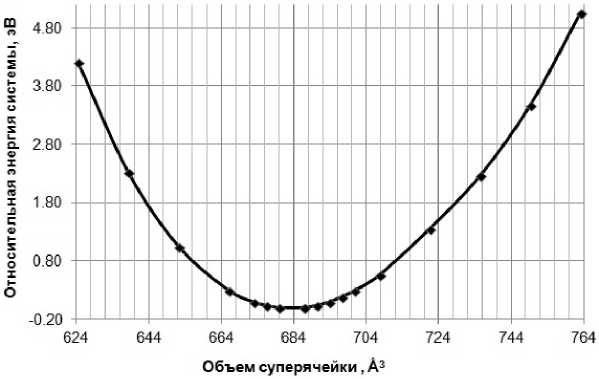
Рис. 4. Зависимость энергии системы от объема суперячейки

мы отличается незначительно. Поэтому для обоих случаев была проведена релаксация положений отдельных атомов в суперячейке до тех пор, пока результирующая сила на каждом атоме не стала меньше 0,025 эВ/Å. Было получено, что более низкой энергией обладает система с объемом 679,924 ų (–2 % от исходного объема). После определения оптимального объема системы необходимо было найти значения параметров решетки ( a , b , c ). Была проведена оптимизация параметра c при постоянных значениях объема системы ( V ) и отношения a / b (рис. 5). Исходные параметры были следующими:

a =5,037; b =8,037; c =16,836 Å;

a = 93,9451°; p = у = 90°.

Как видно из рис. 5, требованию минимального значения энергии системы отвечает параметр решетки c = 17,173 Å (+2 % от ис- ходного значения). Именно эта структура была отрелаксирована, и были получены следующие параметры:

a =4,987; b =7,957; c =17,173 Å;

a = 93,9451°; p = у = 90°.

Дальнейшее изменение параметров решетки приводит к несущественному изменению энергии (менее 0,01 эВ). Параметры решетки для цементитной области отличаются от экспериментальных данных, но незначительно:

a = 4,987 менее 2 % (5,088 Å) [13], b = Va2 + c2 =7,957 менее 2 % (8,118 A), c = 8,197 Å менее 1 %.

Для ферритной части постоянная решетки соответствует значению 2,84 Å, что хорошо согласуется с экспериментальным значением 2,86 Å [21] и оптимальным значением согласно первопринципным расчётам 2,84 Å [22].

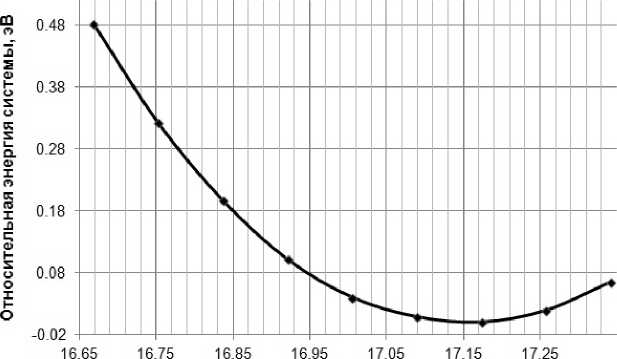
Параметр решетки с, A

Рис. 5. Зависимость энергии системы от параметра c

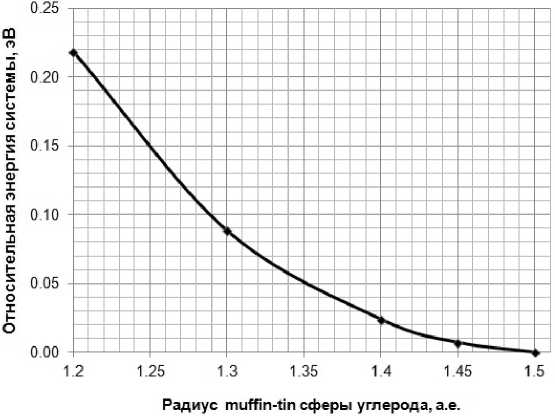
Рис. 6. Зависимость полной энергии системы от R mt углерода

Физическая химия и физика металлургических систем

Таким образом, площадь границ раздела двух фаз была равна 39,6 Å2/ячейку.

Затем необходимо было определить оптимальный параметр muffin-tin сферы для углерода (для чистого железа уже был найден этот параметр, R mt (Fe)=2,0 a.e. [22]). Для этого с ранее оптимизированными параметрами была получена зависимость полной энергии системы от R mt углерода (рис. 6).

Из графика видно, что увеличение R mt (С) свыше 1,45 приводит к незначительному изменению полной энергии (менее 0,01 эВ), и, следовательно, оптимальным значением является R mt (С) = 1,45. Тогда параметр R mt K max , контролирующий сходимость, равен 7,25.

После определения параметров моделирования проводилась основная релаксация положений отдельных атомов в системе в соответствии с силами Хеллмана – Фейнмана до тех пор, пока результирующая сила на каждом атоме не становилась меньше 0,01 эВ/Å. Все это обеспечивает погрешность результатов расчетов не более 0,01 эВ.

Определение энергии формирования границы

Одной из наиболее важных характеристик перлита является энергия формирования межфазной границы, поскольку эту величину можно измерить экспериментально, и она содержит основную информацию о процессах взаимодействия на границах раздела двух сред. Энергия формирования межфазной гра- ницы феррит/цементит определялась соотношением [23]:

E Fe/Fe₃C - E Fe - E Fe₃C γ Fe/Fe₃C =

где E _{Fe/Fe C} - полная энергия системы, содержащей межфазную границу феррит/цементит; E _Fe - полная энергия объемного кристалла феррита; E _{Fe C} - полная энергия объемного кристалла цементита; S - площадь межфазной границы.

Рассчитанная энергия межфазной границы феррит-цементит (4) составила 0,594 Дж/м2, что хорошо согласуется с экспериментальными данными (0,700±0,300 [24], 0,740 [25], 0,500±0,360 [26], 0,690 Дж/м2 [27]) и теоретическими значениями, полученными для ОС Багаряцкого (0,450 [28], 0,615 Дж/м2 [29]).

Была также исследована зависимость среднего магнитного момента атомов железа и межплоскостного расстояния вблизи межфазной границы от номера рассматриваемой плоскости (рис. 7). Из рис. 7 видно, что наблюдается хорошая корреляция между значениями магнитного момента и межплоскостным расстоянием для атомов железа. В ферритной части магнитный момент практически не изменяется и уменьшается по мере приближения к границе раздела фаз. В цементит-ной области зависимость среднего магнитного момента от номера плоскости носит осциллирующий характер. Это связано с тем, что це-

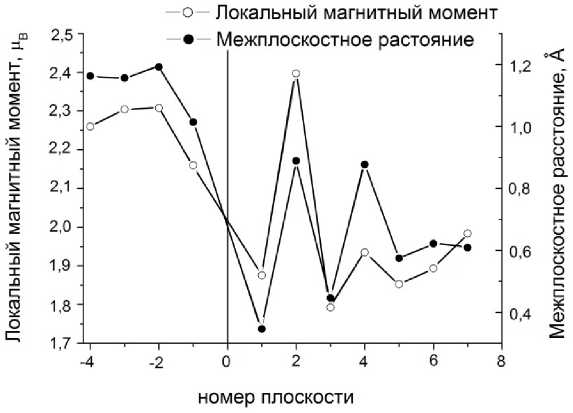
Рис. 7. Сравнение зависимостей локальных магнитных моментов Fe и расстояний между слоями атомов Fe от номера атомного слоя. Вертикальная сплошная линия показывает положение межфазной границы. Отрицательные номера плоскостей соответствуют ферритной фазе, положительные – цементитной

ментитная часть представляет собой чередование двух слоев железа и одного слоя углерода. Поскольку в межфазной области расположение атомов железа более рыхлое, то приповерхностные слои в цементитной части смещаются по направлению к границе раздела, и при этом два слоя Fe, между которыми отсутствует углерод, сближаются, а два других расходятся. Таким образом, наблюдается флуктуационное поведение межплоскостного расстояния вблизи границы относительно среднего значения.

Заключение

В работе построена модель межфазной границы феррит/цементит с ориентационным соотношением Исайчева. Определены оптимальные параметры моделирования данной системы, позволяющие достичь высокой точности. Вычислена энергия формирования межфазной границы, оказавшаяся равной 0,594 Дж/м2, что находится в хорошем согласии с имеющимися в литературе данными, как экспериментальными, так и теоретическими. Для магнитных моментов и межплоскостного расстояния для атомов железа в двух решетках (феррита и цементита) наблюдается хорошая корреляция: с уменьшением расстояния магнитный момент Fe уменьшается, и наоборот.

Исследование поддержано грантом Российского научного фонда № 16-19-10252.