Аберрации синтезированных дифракционных линз, вызванные ошибками их изготовления

G = ----,                                                                              С2)

2f 8f о о гДе ^0 * расчетное фокусное расстояние ДЛ на длине волны Ао, г - расстояние в плоскости линзы от ее оптической оси.

из выражения связан с f₀ и А_о а * Г* Г. к _ к

2f'   8f*3

о о

Для описания

С2) следует, что радиус k-й изофазы структуры идеальной ДЛ уравнением изофаз при наличии ошибок синтеза структуры введем полярные координаты в плоскости ДЛ р и 9, отсчитываемые от расчетного центра кольцевых зон и полярной оси 0Y, соответственно. Тогда координата р^ k-й изофазы может быть легко выражена через радиус соответствующей изофазы идеальной линзы:

Рк * гк * iok'                                                                  <А> где Дрк * ошибка позиционирования к-й изофазы.

В приближении аберраций третьего порядка, а также при условии, когда

Дрк « г, из выражения (4) следует, что rk = °к • 2pkiok;

. .                ■

Г. = Рь/ к к'

а сама ошибка может быть представлена в виде

Дрк = Дгк + Ус к cos О + Ек cos2 О,(6)

где Дгк - отклонение радиуса к-й изофазы от расчетного значения; ус к - смещение центра к-й изофазы; Ек - величина, характеризующая эллиптичность к-й изофазы и равная разности ее полуосей.

Подставив соотношения (5>. (6) в (3) получим уравнение к-й изофазы при наличии ошибок позиционирования

Pl     Pl     Pl

------з* тт (Аг. + у . cos О + е. cos Э) = —у2- •(7)

2t;   ее    о к с'к

Эйконал записи структуры ДЛ, изофазы которой описываются уравнением С?), имеет вид

I               О2      РЦ Р

G Ср/О,у ) = к— - ---j - — (Дг + у cos О + е cos О) .(8)

°       *2^  8f; f*

Сравнивая выражения (2) и (8), видим, что при наличии ошибок позиционирования ДЛ формирует аберрированный волновой фронт, а его волновая аберрация описывается соотношением

Д60 (Р/О,ус) = -^-(Дг + ус cos О + Е cos2 О).С9)

f о

Для оценки максимально допустимого значения каждой из рассматриваемых ошибок воспользуемся критерием Штреля, согласно которому сфокусированное пятно практически не отличается от дифракционно ограниченного, если нормированная интенсивность в дифракционном фокусе не меньше 0,8 [io] . Кроме того, как это было оговорено выше, будем считать, что ошибки позиционирования являются степенными функциями апертуры ДЛ, т.е. в рассматриваемом приближении могут быть представлены в виде

Дг(р) = В-ра; у (р) = Ора;

а                                                                          1101

е(р) = А-ра, где А, В, С - константы; 0 < а < 3.

Тогда при отклонениях радиусов изофаз кольцевых зон от расчетных значений получаем, что

X

А г = Ь Са) * ------- ~ Ь(а)Д ,(11)

max            .    ।min’ t9 °А'

где

. ,       Са+3)Са+5)     /а+2    ,   , ..,

ЬСа) = -------------- • V -57г- ; (а * 1),11 с)

, 2     .              20’ па - 1

ДГтах ~ максимально допустимое отклонение радиуса изофазы от расчетного значения на краю ДЛ; Од, - апертурный угол в пространстве изображений; Am^n * период структуры на краю ДЛ.

При этом дифракционный фокус линзы смещается вдоль ее оптической оси и Отстоит от параксиального фокуса на величину

• △ г

24(а+1)         max                                                     (13)

Д т = -------------- (а+3)(а+5) tg од,

Отметим, что при а = 1, т.е. при линейной зависимости ошибки Дг от апертуры ДЛ, как следует из выражения (9) с учетом первого из соотношений (10), волновая аберрация линзы представляет собой аберрацию расфокусировки. Она, не ухудшая качества изображения, приводит к изменению фокусного расстояния ДЛ на величину, определяемую формулой (13). При а * 1 волновой фронт, формируемый ДЛ, искажен сферической аберрацией и, в частности, при а = 3 - сферической аберрацией Зей- деля .

Если ошибка позиционирования такова, что приводит лишь к неконцентричности кольцевых зон структуры ДЛ, радиусы изофаз которой удовлетворяют уравнению (3), то допуск на максимальное смещение центра крайней изофазы где

у с , та х

= с (а)

tg

~ с(а)Л

min

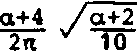
(а * 0) .

^15)

Дифракционный же фокус смещен вдоль оси 0Y и отстоит от параксиального фо куса на величину

Ду'

4у

'с,тах а+4

Очевидно, что при а = О, т.е. когда, несмотря на смещение, зоны остаются концентричными, линза формирует неаберрированный волновой фронт. При всех остальных же значениях а волновой фронт, формируемый ДЛ, искажен аберрациями типа комы и, в частности, при а = 2 - комой Зейделя.

При ошибках позиционирования, приводящих к эллиптичности изофаз, максимально допустимое знамение разности полуосей крайней изофазы структуры линзы

А

= а (а) ----^-— «в а(а)«А . z(17)

max               1min'

t9 °A'

где

а(а) (а+3)(а+5) У----2(а±2)           .

n        5(3au+ 6a3+90a3+ 240a +227)

При этом дифракционный фокус смещается вдоль оси линзы на величину

• △ f' = _12Со±12-- Ееах .

°    (a+3)(а+5) t g Од,

В отличие от вышерассмотренных случаев линза с эллиптичными зонами формирует аберрированный фронт при любом значении а и, в частности, при a = 1 качество изображения ограничено астигматизмом Зейделя, а при a = 3 - аберрацией типа птеры пятого порядка [э].

Таким образом, результаты данной работы позволяют прогнозировать аберрации синтезированных ДЛ, оценивать их качество, а также выработать требования к точностным характеристикам генераторов изображения, используемых для синтеза зонной структуры.