Аберрации второго порядка градиентной среды: методы расчета

Покажем, что аналогичными свойствами обладают градиентные Среды с функцией распределения квадрата показателя преломления (ПП) вида:

n 2 ( ^x , У , ^z ) = ( n о ( ^z ) ) 2 ⁵ N i ( ^z ) ( ^x 2 ⁵ У 2 ) ⁵ ₃₂  (1)

+ N ₂ ( z ),J ( x ² + y ² ) + N 3 ( z ) ( x ² + y ² ) + ... + .

Согласно [3] ход реального луча в градиентной среде описывается системой дифференциальных уравнений:

dT dt

= 2 v ( n ² ( R ) ) = n ( R )v n ( R )

— = T (R) dt

где n (R) dt = (dx )2 +(dy )2 +(dz)2 ;

R = (x; y; z)T - радиус-вектор точки (x;y;z) на траек- тории луча;

T = ( p; q; l) T = n (R )(cos a;cos e;cos Y) T -      вектор оптических направляющих косинусов; а; в; у - углы, оброазованные касательной в точке (x;y;z) с осями координат OX; OY; OZ соответственно;

T z А ( dn dn dn ) V n (R) = I —;---;— I

(dx dy dz J градиент ПП в точке

(x;y;z).

Рассмотрим бесконечно близкий к оптической оси луч. Для такого луча координаты точки на траектории и оптические направляющие косинусы можно представить в виде:

R = R + 5 R ;

T = T , axial

+ 5 T ,

где R axiai = ( 0;0; ^z ) ^T ; T axiai = ( ° ° n о ( ^z ) ) ^T ;

5 R = ( 5 x ; 5 y ; 5 z ) T и 5 T = ( 5 p ; 5 q ; 5 l ) T - бесконечно малые первого порядка малости.

Дифференциальные уравнения (2), (3) при бесконечно иалых 5 R и 5 T преобразуются в выражения:

n о ( z ) d i p = N i ( z ) 5 x ; dz	(4)
n о ( z ) d T q = N - ( z ) 5 у ; dz	(5)
/ x d 5 x _ n о ( z )—t" = 5p ; dx	(6)
l A d 5 y e n о ( z )t" = 5 q . dx	(7)

Система уравнений (4), (5), (6), (7) описывает ход параксиального луча в градиентной оптической среде [3]. Если обозначить через ц ( z ) n ( z ) углы параксиального луча с оптической осью в саггиталб-ном сечениях соответственно, то :

⁵ p ( z ) = - n о ( z ) ^ ( z )

5 q ( ^z ) = ^{- n} о ( ^z ) n ( ^z )

Вновь рассмотрим бесконечно близкий к оптической оси луч, учитывая теперь величины первого и второго порядка малости. В этом случае

R = R_m +5 5 R + - 5 ² R axial            ₂

T = Taxiai + 5T 5 2 52 T где 52R = (52x;52y;52z)T ; 52T = (52p;52q;521)T -бесконечно малые второго порядка малости.

Уравнения (2), (3) раскладываем в ряд Тейлора, сохраняя величины до второго порядка малости. После преобразований полученных выражений с учётом (4)-(7) имеем:

n₀ ( z ) d ^ d-P. = N 1 ( z ) 5 ² x + 3 N 2 ( z ) 5 x ^( 5 x ) ² + ( 5 y ) ² (8) ⁿ о ( ^z ) d ^ dT = N ¹ ( ^z ) 5 ² y ^{+ 3} N 2 ( ^z ) 5 y^ ( 5 x ) ^{2 +} ( 5 y ) ^{2 (9)}

n о (z) dyq = 5 2 p dz

/ \ d5 q e21 \ n о (z)™=5q dz

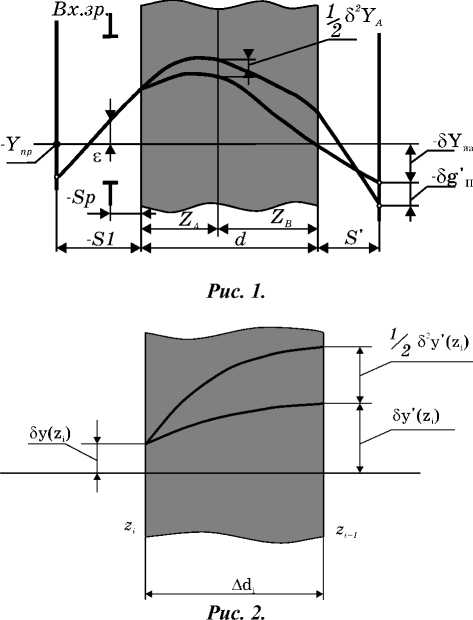
Рассмотрим находящийся в однородных средах пространства предметов и пространства изображений оптический элемент, представляющий ограниченную плоскими поверхностями градиентную среду с распределением ПП (1). Рассчитаем ход через этот элемент бесконечно близкого к оптиче- ской оси луча с учётом величин до второго порядка малости (рис. 1).

В среде пространства предметов имеем [3]: ⁸ Qi = - n n i = ( m - y _np ) n i /( S_p - S i ) ;           8 ² q - = 0;

8 p 1 = - n p 1 = Mn 1 Д S _p - S 1 ); 8 ² p 1 = 0. На первой поверхности элемента:     8 x 1 = S p 1 ;    8 ² x 1 = 0 ;

8 y 1 = S 1 n ; 8 ² y 1 = 0. Преломление луча на этой поверхности описывается       формулами:

-np = 8p- = -nо (0)p(0) = 8p(0);      82p(0) = 0 ;

- n n 1 = 8 q 1 = - n ₀ ( 0 ) n ( 0 ) = 8 q ( 0 ) ; 8 ² q ( 0 ) = 0. Значения координат    8 x 2 = 8 x ( d ) ;    8 y ₂ = 8 y ( d ) ;

8 ² x ₂ = 8 ² x ( d ) ; 8 ² y ₂ = 8 ² y ( d ) и оптических направляющих косинусов 8 p ₂ = 8 p ( d ) ; 8 q ₂ = 8 q ( d ) ; 8 ² p ₂ = 8 ² p ( d ) ; 8 ² q ₂ = 8 ² q ( d ) в точке встречи луча со второй поверхностью (z=d) находятся в результате интегртрования дифференциальных уравнений (4)-(7) и (8)-(11) при начальных условиях: 8 x ( 0 ) = 8 x , ;         8 p ( 0 ) = 8 p_x;         8 y ( 0 ) = 8 y - ;

8 q ( 0 ) = 8 q 1 ;       8 ² x ( 0 ) = 8 ² x 1 ;       8 ² p ( 0 ) = 8 ² p 1 ;

8 ² y ( 0 ) = 8 ² y 1 ; 8 ² q ( 0 ) = 8 ² q 1 . Преломление луча на второй поверхности описывается формулами: - n ₃ p ₃ = 8 p 3 = - n ₀ ( d ) p ( d ) = 8 p ( d ) = 8 p ₂; 8 ² p 3 = 8 ² p ( d ) ; - n 3 n 3 = 8 q 3 = - n ₀ ( d ) n ( d ) = 8 q ( d ) = 8 q ₂; 8 ² q ₃ = 8 ² q ( d ) .

Координаты точки встречи луча с плоскостью изображения с учётом первых и вторых порядков будут:

x  = 8x + — 82 x u3u32 u3

y = 8y +—82 y u3u32 u3

где

8 x _vk = 8 x ₂ + 8 p 3 S'/ n 3 ; 8 ² x _vk = 8 ² x ₂ + 8 ² p 3 S 7 n 3 ;

⁸ у_Ц к = ⁸ y 2 ^{+ 8} q з ^S 7 ⁿ 3 ; ^{8 2} y_VK = ^{8 2} y 2 ^{+ 8 2} q 3 ^S 7 ⁿ 3 •

На основании (12) и (13) аберрации второго порядка луча равны:

⁸ g ‘ I = 2 ^{8 2} yu 3 ;

8 G ‘, = - 8 ² x II

. u 3

Таким образом, задачу расчета аберраций второго порядка для градиентных сред можно считать решенной. Существенным недостатком изложенной методики является необходимость решения системы дифференциальных уравнений (8)-(11).

Рассмотрим усовершенствованную методику рассчета аберраций второго порядка, свободную от указанного недостатка. С этой целью разделим градиентную среду плоскостью на части А и В. В результате рассчета величин второго порядка малости через часть А в плоскости раздела частей А и В имеем 8 ² xA = 8 ² x ( z_A ) ; ^{8 2} y A = ^{8 2} y ( z A ) ; ^{8 2} p A = ^{8 2} p ( ^za ) ; ^{8 2} q A = ^{8 2} q ( ^za ) •

Продолжая расчет величин второго порядка малости через часть В при начальных условиях ^{8 x}BO = ^{8 x} A ; ^{8 y}BO = ^{8 y} A ; ^{8 p}BO = ^{8 p} A ; 8 ² q _BO = 8 ² q A , в плоскости изображения получим: ^{8 x} u 3 ab ; ^{8 y} u 3 ab ; ^{8 x} u 3 ab ; ^{8 x} u 3 ab •

Можно поступить иначе. Если в качестве начальных условий для расчета величин второго по-лядка малости через часть В принять 8 ² x _BO = 8 ² y _BO = 8 ² p _BO = 8 ² q _BO = 0 , то в плоскости изображения        определим        величины

82x    ; 82yu38 82p3B; 82q3B.   Рассчитаем также u3AB        B через часть В до плоскости изображения параксиальный луч с начальными координатами 82 xbo = 82 x A;      82 yBO = 82 yA;      82 pbo = 82 pA;

82qBO = 82qA; в результате в плоскости изображения получим 825си 3ab ;82 y ;82p3 ab ;823 ab • u 3 ab

Т.к. общее однородное решение системы дифференциальных уравнений (4)-(7) подобно общему однородному решению системы дифференциальных уравнений (8)-(11), то выполняются равенства:

• ⁸ xu 3 AB = ⁸ xu 3 B ^{+ 8} x^ u 3 AB ^;

• ^{8 y} u 3 AB = ^{8 y} 3 B ^{+ 8 y} u 3 ab ;

• ^{8 p} 3 AB = ^{8 p} 3 B ^{+ 8 p} 3 AB ;

• 8 ² q 3 AB = 8 ² q 3 в + 8 ² q 3 ab •

Для ЦООС в параксиальной области известен обобщеный инвариант Гюйгенса [3], справедливый при любом значении z в любой среде:

Q 0 = nAH - нД h =

= n 0 ( z ) a ( z ) ^H ( z ) — n 0 ( z ) ^e ( z ) h ( z ) = , (14) = n₃ a ₃ H 2 - n 3 p ₃h 2 = n₃ a ₃ H u 3 - n₃ P ₃hu 3

где ( a ; h ) и ( P ; H) - углы и высоты двух произвольных параксиальных лучей; h u З и H u З - высоты этих лучей; h 2 и H 2 - высоты этих лучей на второй поверхности градиентного элемента.

Примем, что ( a ; h ) - угол и высота апертурного (первого вспомогательного [3]) параксиального луча, который пересекает плоскость изображения при h _u З =0 [3]. Тогда высота H _u З в плоскости изображения другого, входящего в инвариант (14) па-раксимального луча определяется как

Н = -Q ⁰-, u ^{3    a} 3 n 3

где a 3 - угол первого вспомогательного луча в пространстве изображений.

Величина 32yu3AB находится из расчета пара- ксиального луча, поэтому для нее на основании уравнения (15) можно записать:

³ yu 3 AB

Ly a3 n 3 ’

где L y - меридиональный квазиинвариант [3]:

L y = ^{3 2} у ( ^zA ) n о ( ^zA ) ^a ( ^zA ) + h ( ^zA ) ^{3 2} q ( ^zA ) .

Аналогично для саггитального сечения:

2 x

3 xu 3 AB   „ a3 n 3

где L x - сагиттальный квазиинвариант [3]:

Lx = 32 x ( zA ) n0 ( zA ) a ( zA ) + h ( zA ) 32 P ( zA ) .

Очевидно, что градиентную среду можно разделить не на две, а на любое количество m частей. Меридиональный и саггитальный квазиинварианты для каждой i -й части Среды определяются уравнениями:

L yi = ^{3 2} у ' ( z i ) n 0 ( z i ) ^a ( z i ) + h ( z i ) ^{3 2} q ' ( z i ) ;

Lxi = 32 x' ( zi ) n0 ( zi ) a ( zi ) + h ( zi ) 3 2 P '( zi ) ,

где zi+1 = zi + Аdi; a (zi+1) = a' (zi); h (zi+1) = h '(zi).

При этом в начале каждой i -й части среды примем: 3 ² x. = 3 ² y. = 3 ² p. = 3 ² q i = 0 .

Интегрированием системы дифференциальных уравнений           (8)-(11)           находим

3 ² x '( z i ) ; 3 ² y '( z i ) ; 3 ² p '( z i ) ; 3 ² q '( z i ) в конце каждой i -й части Среды (рис. 2). Суммарно от всех m частей градиентной Среды имеем:

• ^a 3 n 3 ³ 2 xu ₃ ^^L;                       ⁽¹⁶⁾

i = 1

m a3 n332 yu 3 = ^ Lyi i=1

Рассмотрим случай, когда величина A d i бесконечно малая. В этом случае для нахождения величин 3 ² x ‘ ( z i ) ; 3 ² y ‘ ( z i ) ; 3 ² p ‘ ( z i ) ; 3 ² q ' ( z i ) воспользуемся разложением в ряд Тейлора и с учетом (8)-(11) получаем:

3 ² x' (z .) = 3 ² x zz_l ) + ³³ x    A d. =

^{( , )          ( , )} dz z = z i      i ;                      (18)

= 3 2 x ( zi ) + 3 2 p ( z ) A di / n 0 ( z )

^{3 2} У ' ( ^zi ) = ^{3 2} У ( ^zi ) ⁺

d 3 2 y
	=
dz	z = z i      1 ;                     (19)

= 3 2 У ( zi ) + 32 p ( zi ) Adi /n 0 ( zi )

3² p ‘ ( z i ) = 3² p ( z i ) + d^ dz

A d i =

= 32 p (zi) + (N1 (z) 32 xi +

+ 3 N2 (zi) 3xi ^ (3xi)2 +(3yi )2) A di / n 0 (zi)

3 ² q ‘ ( z^ = 3 ² q ( z . ) + d ^ q dz

A d i =

z

= 32 q (zi) + (N1 (z) 32 yi +

+ 3 N2 (zi) 3yi ^ (3xi)2 +(3y,-)2)A di / n 0 ( zi )

;

.

Выражения (18)-(21) можно преобразовать, принимая во внимание, что

3 2 x (z) = 3 2 y (z) = 3 2 p (z) = 3 2 q (z) = 0 : 32 x'(zi. ) = 0; 3 2 y ‘(zi ) = 0; 32 p' (zi) = 3 N2 (zi) 3xi -J (3xi )2 +(3yi )2 A di /n 0 (zi); 32 q' ( z. ) = 3 N2 ( z. ) 3у. yj (3xJ2 +(3у.)2 A di /n 0 (zi.);

L xi = h ( ^zi ) ³ N 2 ( ^zi ) ^{3 x}i J ( ³ x ) ^{2 +}( ³ у , -) ^{2 a} di In 0 ( z ) ;⁽²³⁾

L yi = ^h ( ^zi ) ^{3 N} 2 ( ^zi ) ³ У. ^ ( ^{3 x}i ) ^{2 +} ( ³ y , -) ^{2 A} di Iⁿ 0 ( ^zi ) .⁽²⁴⁾

Заменяя в (16), (17) суммирование на интегрирование и учитывая (23), (24), получаем:

2 a 3 n 3 3 g ‘ I =

d h ( z ) 3 N2 ( z ) 3У ( z ) J (3x ( z ))2 +(3У ( z ))2

=j-----------TH-----------dz

0                       n ^{0 (} z )                           ; (25)

2 a ₃ n ₃ 3 G I'I =

d h (z) 3 N2 (z) 3x (z) J (3x (z ))2 +(3y (z ))2

= j-----------Гы-----------dz

• ^{0                         n 0 ( z} )                            . (26)

При этом 5 g’_n и 5 G’ ii включают в себя все аберрации луча, в т.ч. дисторсию.

Рассмотрим расчет меридиональной сферической аберрации второго порядка. Из уравнения (25) при 5 x= 5 p=0; 5 y(z)=h(z); 5 q(z)=-n₀(z) a (z) получаем:

d 3 N ₂ ( z ) ( h ( z ) ( ³

2 a 3 n 3 8 g ‘ с _ф = J                 _dz .         (27)

0        ⁿ 0 ^{( z} )

Дисторсия второго порядка определяется уравнением

d

^{2 a} 3 n 3 ^{8 g} II Dist = J

3N2 (z)( H (z)( H (z) h (z)(3

dz ,(28)

n 0 ( z )

где ( в ; Н ) - угол и высота полевого параксиального луча (второй вспомогательный луч [3]).

Может быть доказано, что если градиентный элемент ограничен не плоскостями, а сферическими поверхностями, то формулы (25) и (26) остаются в силе, т.к. сферические поверхности не вносят аберраций третьего порядка, а характерные для теории аберрации третьего порядка поверхностные составляющие [3] в теории аберрации второго порядка отсутствуют.

При наличии в оптической системе нескольких градиентных сред поперечная аберрация второго порядка описывается выражениями:

k

• 2а'n ^g I, = £ L yj ;

j = 1

k

• 2 а'n 8 G II = ^ L _xj .

j = 1

где k - число градиентных сред: a‘ - угол первого вспомогательного луча в пространстве изображе- ний; меридиональный и саггитальный квазиинварианты для каждой j - среды определяются на основании вышеприведенных выражений:

d j

L , = J

h (z)3 N2 (z) 8, (z )V(8x (z ))2 + (8У (z ))2

ⁿ 0 ( ^z )

dz ; (29)

djh ( z ) 3 N2 ( z ) 8x ( z )V(8x ( z ))2 +(8, ( z ))2,

L j =^J------------------ n rc z )------------------ ^dz -⁽³⁰⁾

Все подинтегральные величины в (29), (30) соответствуют j -й среде.

Для градиентной оптической системы в виде градиентного стержня с плоскими поверхностями были вычисленны по формулами (25)-(28) поперечные аберрации второго порядка, а также аберрации реальных лучей. Длина стержня 23.5мм; функция распределения П: n ² ( x , y , z ) = = 1.5 ² - 0.01 ( x ² + y ² ) - 0.0005 ^(x ² + y ² ) . Предметная плоскость бесконечно удалена от первой поверхности стержня; входной зрачок расположен на расстоянии -Sp=5 мм. Плоскость изображения совпадает с плоскостью Гаусса S’=41.29684*10^-3 мм.

В таблице 1 приведены аберрации осевого пучка, вычисленные на основании расчета реальных лучей и с использованием формулы (27).

Дисторсия второго порядка, вычисленная для угла поля ю =-30’ с использованием выражения (28) и на основании расчета реального луча, равна 5 g’ D _ist=-0.47599*10^-3 и 5 g’ iiD _iSt=-0.47970*10 " ³ соответственно. В таблицах 2 и 3 приведены значения аберрации наклонного пучка ( ю =-30’) в меридиональном и сагги-тальном сечениях, определенные на основе расчета хода реальных лучей и по формулам (25), (26).

Высоты лучей во входном зрачке подобраны таким образом, чтобы влиянием аберрации третьего, четвертого и более порядка можно было пренебречь. Результаты расчета по формулам (25)-(28) теории аберрации второго порядка имеют хорошее совпадение с результатами расчета реальных лучей.