Аберрация света (ВЕРСИЯ - ЭТО)

Вывод формул аберрации света на основании ВЕРСИИ Элементарной теории относительности. Физическая интерпретация процесса аберрации света.

Содержание

• 1.    Определение

• 2.    Вывод формул для углов наблюдения

• 3.    Аберрация света

• 4.    Физический процесс регистрации событий

• 5.    Критические углы наблюдения

• 6.    Заключение

• 5.2    Фиктивный угол наблюдения собственного источника света наблюдателем N 1 из начала координат основной ИСО.

  

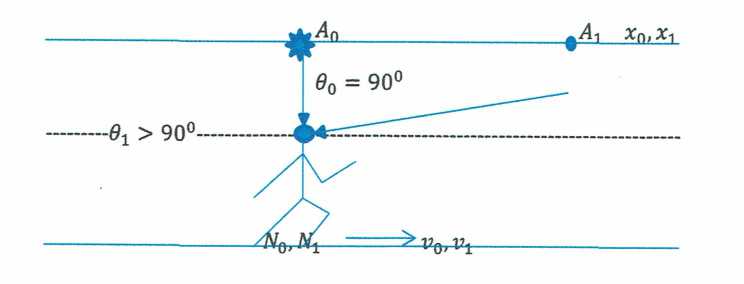
  Рис. 5.

  
  

  В этом случае: cos 0_О = 0, sin 0_О = 1, 0_О

  
  

  = "/и -

  
  

  cos 0 1

  sin 0 1

  
  

  cos 9₀-Р

  1—Р cos 9₀

  
  

  ^- Р ,

  
  
  
  

  У1-Р² sin9 o 1—Р cos 9₀

  
  

  . ।       - ■ .

  
  

Принятые сокращения.

ЭТО — Элементарная теория относительности.

СТО — Специальная теория относительности.

ИСО — Инерциальные системы отсчёта.

1.    Определение

П.1 Аберрация света. Видимое смещение неподвижного объекта при наблюдении его в разных системах отсчёта называется аберрацией света. На рисунке 1 представлена графическая иллюстрация такого смещения. В зависимости от скорости движения приёмника света угол наблюдения объекта над горизонтом меняется. В качестве неподвижной точки принимается начала координат собственной ИСО. Полученные результаты будут справедливы и по отношению к любым другим неподвижным точкам. Неподвижные точки излучают световой сигнал, который улавливают подвижные наблюдатели ^(Л^) соответствующих ИСО (основной или параллельной) под определённым углом 9 к траектории движения приёмника, рис. 1.

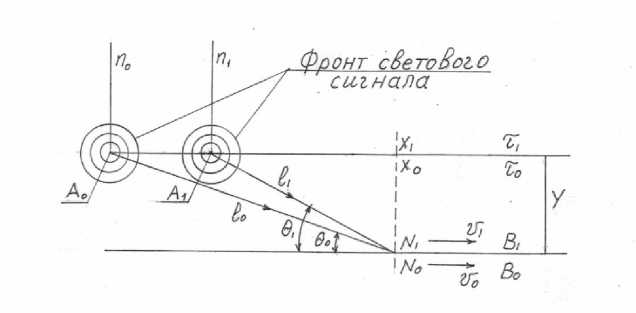
Рис. 1

Траектории В₁, В_о отстоят от осей Ч, То на одинаковом расстоянии Y абсолютного пространства, 1₁,1 о — расстояния между центрами координат и наблюдателями в собственных ИСО.

2.    Вывод формул для углов наблюдения

Основой вывода формул углов наблюдения являются преобразования координат в варианте ВЕРСИЯ — ЭТО. Чтобы отделить эти преобразования от преобразований Лоренца в СТО, назовём их кратко Лоренц – ВЕРСИЯ.

Из рис. 1 определим косинусы углов наблюдения:

О — Х0 — Х0        О — Х1 — Х1

COS ио — , —     , COS ui — _ —     ,

? 0     ^с0^                   ^ 1      ^С^1

где C o — С - постоянная скорость света в основной ИСО ( ~ 30 * 10 ⁷ m/c ); с₁ — с/(1 + ■^г) — не постоянная скорость света в параллельной ИСО.

Используем преобразования координат Лоренц [2, таблица 1].

Для наблюдателя N o основной ИСО, прямые преобразования: i                        _ 1

• 1)    Хо — Х1(1+1)2 + Voti(1+ 5)4 .

  _ 1

  2)   t o — t i (1+ C l ) ² + X i

  
  

  M1+ «< .

  
  

Разделим первое уравнение на второе и на скорость света в основной ИСО:

cos 6₀

X o

Cto

•J ,/) ,'■;,/;

ct1y    c ² J    c у C²y

——

_1              1

(1+4)- 2 + x ⁱ 'o (1+4)² у c² I     ct1cy   c ² у

.

Используем выражения (1) и обозначим соотношение — = /?.

В результате последовательных преобразований получаем между углами наблюдений с точки зрения наблюдателя N_o : cos 0_О — ^f+,^cos9 1 , sin 0_О — V1 — cos²6₀ .

⁰     1+fcos9 1 ,         и \             и

связь

Аналогично для наблюдателя N₁ обратные преобразования:

параллельной

ИСО,

% 1 =

t 1 ^—

X o -V o t o 1              ,

ИГИ)

to-_Y„ 'o

“•o ^Xo _c 2

_1 ИГИ)

.

Разделим первое уравнение на второе параллельной ИСО:

и

на скорость

света в

- ^%1 - X o -V o^ cos У^ —    —      v₀

C 1 t 1     t o -X oc2

И) ■

Xo '0 cto c 1 ^X o'o . cto c

Используем выражения (1). В результате последовательных преобразований получим связь между углами наблюдений с точки зрения наблюдателя ^:

cos О, — cos^ ^f , sin О, — J1 — COS ² 0_t .

¹      1-fcos9_o ,             ¹ -V               ¹

3. Аберрация света

Формулы для углов наблюдения в ВЕРСИИ и СТО совпадают полностью:

cos 9₀

sin 6₀

f+cos 9 1 1+f cos 9 1 ;

V1-f² sin 9 1

1+fcos9 1 ;

cos У1 — sin У1

cos 9o-f

1-fcos9o ;

= V1-f² sin9 o

1-f cos 9o

Формулы соответствуют варианту движения наблюдателей от источника света. В противном случае скорость V u и Р имеют отрицательные знаки. Разница углов наблюдения называется

углом аберрации а — 0 i — 0q •

Пренебрегая всеми степенями Р^п кроме первой (Р « 1) , получим приближённое выражение для связи углов наблюдения. Косинусы малых углов можно принимать за единицу.

^1-Р2         V^21

sin 81 = sin во 1-^ = sin       = sin во

Умножая числитель и знаменатель на сопряженное выражение (1 + Р) , получим соотношение:

sin 91 = sin во 1+2= (1 + Р) sin во

Для малых углов справедливы равенства: sin 9 1 = 9 1 + 5 1 и sin 9 о = 9 о + 5_о , где 5 систематическая погрешность замены синуса угла на значение самого угла в радианах. Следовательно, можно записать:

5 1 - 5_о = ±Д5 « 0 :

sin 9 1 - sin 9_о = 9 1 - 9_о ± Д5 = 9 1 - 9_о = а

Тогда угол аберрации из уравнения (6) приблизительно равен:

а = Р sin 9_о = ^ 0 sin 9_о = к sin 9_о.                     (7)

Более точное значение аберрации даёт формула:

а = (J 1i| - 1) sin 9 о = к sin 9 о.                     (8)

Постоянная годовой аберрации к для средней орбитальной скорости Земли, принятая Международным Астрономическим Союзом, составляет 20,49552 " угловых секуд.

4.    Физический процесс регистрации событий.

Представим себе длинный коридор, разделённый на две части. Левая часть, это область действия основной системы отсчёта с наблюдателем ^ о. Правая часть, это область действия параллельной системы отсчёта с наблюдателем N 1. Область основной ИСО покрывает область параллельной ИСО. Иллюстрация приведена на рис. 2, 3.

Начало события №1

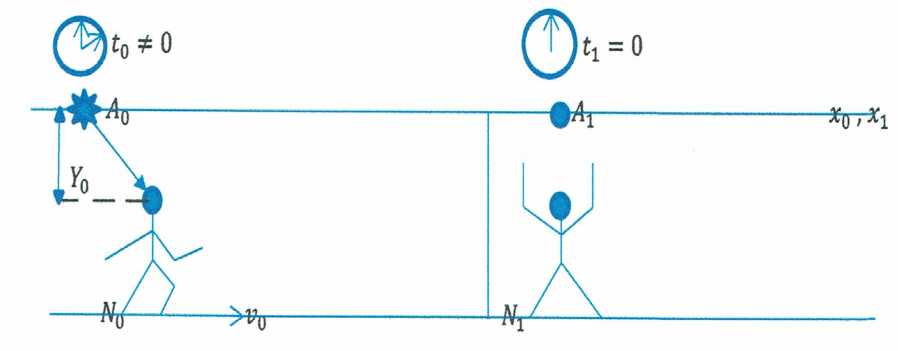
Рис. 2.

Начало события №2

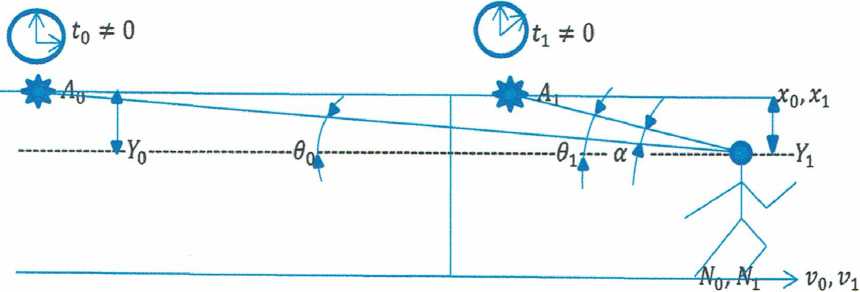
Рис. 3.

Наблюдатель N_o основной ИСО включает источник света в центре собственных координат Л д и запускает часы, событие №1. В основной системе отсчёта начинает протекать время t₀ . Наблюдатель N_o движется в сторону центра координат Л 1, со скоростью V g и непрерывно наблюдает собственный источник света с момента его появления. Его смещение относительно координатной оси Y_o .

Наблюдатель N параллельной ИСО находится на расстоянии Y 1 от центра координат Л 1 в состоянии покоя. Он не видит чужого источника света, его часы стоят, время в параллельной ИСО отсутствует. Когда наблюдатель N g достигает центра координат Л 1, он толкает наблюдателя N 1 . Тот в свою очередь включает источник света в центре собственных координат Л 1 и запускает собственные часы, событие №2. В параллельной системе отсчёта начинает протекать время t 1.

С момента столкновения оба наблюдателя совпадают в пространстве и времени обоих ИСО, перемещаются синхронно, в одном направлении. Каждый из них наблюдает свой источник света в центре собственных координат. У каждого наблюдателя собственные единицы измерения расстояний, времени и скорости движения вдоль общей траектории. Смещения У₀и К 1 в абсолютном пространстве одинаковые. Поскольку пространственные углы в обоих ИСО инварианты, то их единицы измерения в радианах совпадают. Наблюдатель N_o видит начало события в основной ИСО. Наблюдатель N , видит последствия этого события в параллельной ИСО.

Существует частный случай , который широко используется в СТО и ЭТО. Это, когда центры координат А₀, А 1 совпадают в пространстве и времени единой ИСО ( абсолютное пространство в его локальном смысле ). Оба наблюдателя включают свои источники света одновременно. Лучи наблюдения этих источников совпадают. Аберрация равна нулю. Во любом случае свет различают на «свой» и «чужой».

sin 61 = sin 60 , а = 61 — 60 = 0.

В общем случае , сдвиг наблюдения событий во времени вызывает аберрацию лучей наблюдения в пространстве. Точки, в которых наблюдаются события, называются точками наблюдения . События одной ИСО будут наблюдаться в другой ИСО только в том случае, если их последствия реально достигают точек наблюдения. Если последствия не достигают точек наблюдения, то такие события скрыты за горизонтом событий, т. е. в промежутке между центрами координат двух ИСО. Примерами таких событий являются чёрные дыры во Вселенной.

5.    Критические углы наблюдения 5.1    Реальный угол наблюдения собственного источника света наблюдателем N0 на границе с параллельной системой отсчёта.

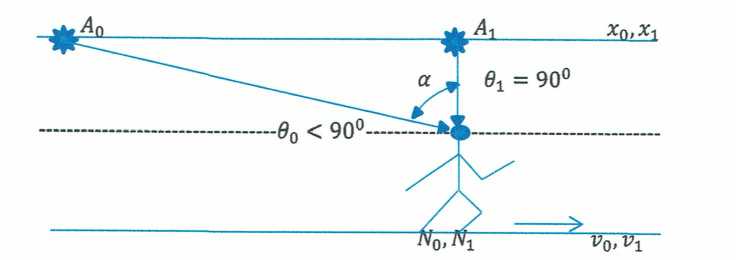
Рис. 4.

В этом случае: cos 01 = 0, sin 01 = 1, 01 = ^^ •

„        /?+cos9!       D....

cos 0« =         = ^

sin 0_O = VEpin^ = yr—g 2,

0      1+/?cos9L

a = | — arc sin 0O.

Максимальное значение аберрации при V o = С и /? = 1, a = 2.

Минимальное значение аберрации при Vo « С и /? ~ 0, a = 0.

Наблюдатель N_o может находится в прошлом, настоящим и будущем времени параллельной системы отсчёта. Угол 0 о зависит также от поперечного смещения У 0. Зная значения У 0, аберрацию С и условное положение центра Д 1 или Д о в основной системе отсчёта, можно вычислить расстояние между центрами координат в масштабах основной ИСО. При очень больших значениях У 0 ситуация с бегунами приходит к виду аберрации далёких звёзд. Векторы скоростей Vo и V 1 направлены перпендикулярно лучам наблюдения.

До ^ Д, - Уо tan a.

Луч наблюдения направлен мимо центра координат А1(01 > 900). Наблюдатель N1 не видит собственного источника света до тех пор, пока угол 01 не достигнет критического значения 900. Угол считается фиктивным по тому, что между центрами координат время в параллельной ИСО отсутствует. Наблюдатель N^He может находится в отрицательном времени собственной параллельной системы отсчёта.

• 1.    Выражения типа « С точки зрения наблюдателя одной системы отсчёта или другой системы отсчёта …. » должны быть тщательно обоснованы. Не везде, где находиться один наблюдатель может находиться и другой.

• 2.    Результаты анализа Лоренц – ВЕРССИИ в части аберрации света совпадают с выводами официальной СТО. Следовательно, ВЕРСИЯ – ЭТО как теория имеет право на существование.

• 3.    Земля с точки зрения аберрации находится в основной ИСО. Аберрацию света далёких звёзд можно наблюдать на Земле только на малых скоростях движения приёмника, т.е. при V o « С .

• 4.    Источники света и наблюдателей всегда можно поменять местами. Неподвижные наблюдатели будут находиться в центрах координат, а в пространстве будет двигаться единый источник света.

• 5.    Наблюдатели не имеют массы, энергетический обмен на границе систем отсчёта между ними не происходит. Этот фактор отличает аберрацию от преобразований Лоренца. Аналогично преобразованиям координат с массовыми точками, «чужой» свет из основной ИСО заменяется на «свой» свет в параллельной системе отсчёта.

Результаты анализа при этом не меняются, но интерпретация физического процесса аберрации усложняется.