About possibility of mixing of liquid metal with external rotational magnetic field

Development and implementation of new technologies for effective mixing of liquid metal is still a vital problem. It is known that duringmixingprocess various ingots are formed with different physical and chemical properties. Development of a new theoretical method for calculation of chemical reaction rate of various impurities in liquid metal is an important task in metallurgy. Various atoms and molecules in liquid metal move on trajectories similar to trajectories of Brown particles. Thus when considering motion of atoms and molecules all degrees of freedom need to be considered equally.

Liquid metal (molten metal of crude-iron and steel) can have density around 7000 kg/m3 at the temperature of about 1600 °C [1 – 3]. Processes of carbon oxidation in liquid metal play very important role, С+О = (CO). It is known that carbonization already begins at temperatures of 400 – 600 °C [1-3]. As the process of carbonization goes on the temperature of molten metal goes down. The melting temperature of iron containing 4.3 % carbon can go down to 1147 °C.Carbon oxide plays an important role in reduction reactions of iron [1-3]:

FFeO 43 ₊ ⁺ CCO ; SO CO CO 2 66807JZT

FeO + CO = Fe +CO 2 - 16060 J/mol.

Methods and equipment

Numerical calculations were carried out on PC using Maple 15 package are used. We expanded an analytical (theoretical) solutionof the differential equation for a Brownian particle into general threedimensional case.

Results

We have received the following new differential model for calculation of interaction rate of С and О atoms in liquid metal dnc        2

F=f ・ d ] ， ² • n c • n o • v rel .

个"•喰Z • Vrel, where di,2 = d2,i = q + q - effective diameters of interacting atoms, % = 0.76-10-10 m-radius of a carbon atom, q = 0.58 • 10-10 m-radius of an oxygen atom, t - time, s.

Average speed of relative motion is defined byequation Vrei = |v2 - vj. In our case v2 二 vc -rr absolute speed of a carbon atom, Vi 二 V° - absolute speed of an oxygen atom.

In molten liquid metal atoms of oxygen and carbon can move freely, so their movements can be described as in molecular-kinetic’s theory. If atoms are partially ionized, then oscillating motion within one crystal cell will be accompanied by transition of potential energy to kinetic energy and back. However, total chaotic movement of atoms will be like movement of a Brownian particle. Average kinetic energy of atoms remains constant and is not lost to potential energy of interaction with atoms.Excluding moments of time where atoms collide, their motion can be described as in molecular-kinetic’s theory.The definition equation for relative speed of motion looks like [4]:

v rel =

8RT ＜丄丄 )]^{12 n} QoR ] ,

where R =8.31 J / (mol*K) - a universal gas constant; Т - absolute temperature, K; 卩 ° , 卩 c - molarmasses of atoms, kg/mol.

The equations (2) and (3) form a nonlinear system of equations, whose analytical solution is:

n c = n c,0 • ^exp [ "ⁿ- ^d 2 ₂ • n o • v rel • ^{t ]} , ^,

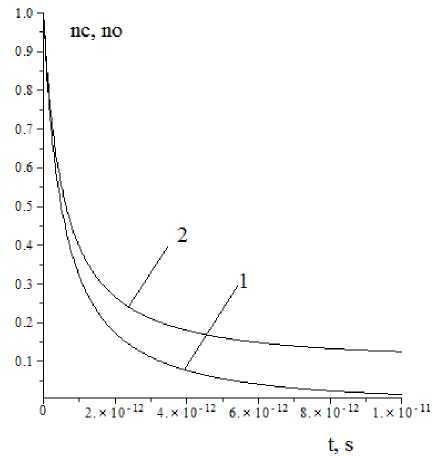
Fig. 1. Change of concentration of carbon – 1 and oxygen – 2 atoms in liquid metal as a function of time very small time interval t~10-11 -10-10 s, Fig. 1. Fig. shows change of relative concentration of carbon and oxygen atoms as a function of time. Element, which has higher initial concentration than the other, decreases more slowly.

If initial concentration of oxygen atoms is taken very small, so that only one collision (one interaction) of С+О is considered at a time, then an estimated time of reduction of carbon concentration can increase up to 10¹² s. By performing calculations at various initial concentrations n o , an estimated time (for reduction of a level of carbon n_CO to 0.5 %) equal to 3 minutes is obtained. Thus it is possible to reduce time of technological processing of liquid metal to level of 1-3 minutes.

Careful attention needs to be paid to the fact that our calculations and results correspond to an ideal case: arrangement of impurity atoms is uniform throughout the volume; there are no retarding factors, such as the inverse reaction of CO decomposition;there are no convective currents (loss of atoms);absence of stagnation zones in molten metal;impurity atoms have equal initial concentrations (nc=no) and so on. In reality not every collision of a carbon atom with an oxygen atom results in formation of a CO molecule.

We have done calculations for 1 m³ of liquid metal with the following initial conditions. Liquid metal has three components: n °b 二 п ғе + n c + n o , pf = 7000 kg/m³, Т=1873 K - density and temperature of liquid metal, n c =0.04* n °b (at 4 %) - mass concentration of carbon, N f© = 7.467 • 10 28 , Nc = N ° = 1.394 - 10 28 - initial total quantity of iron, carbon and oxygen atoms in 1 м 3 of liquid metal. For a carbon atom we obtain: free path length 纵 = 6.714 - 10 ^{- 11} m; average speed v c = 18¹⁰.⁴¹ m/s; diffusion coefficient D e = 4.05 卜 10^-8 m²/s. Similarly, for atom an oxygen atom we receive: 九 o 二 7.916 ・ 10 ^{- 11} ； D o = 4.137^10-8 m^2/s ； v o = ¹⁵67.71 ^m/s, v rei 二 2395.82 m/s.

Thus the problem of more intensive and uniform mixing of all volume of liquid metal, so that all atoms of C and O could enter into reaction simultaneously and in the shortest possible time, is pressing. We see the solution of a problem in application of rotating variable magnetic field.

Fig. 2. Penetration of magnetic field through a piece of a brick

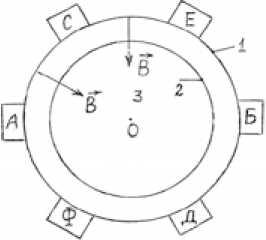
АБ – winding 1, СД – winding 2, ЕФ – winding 3, 1, 2 – external and internal walls of a melting bath, 3 – molten metal

Fig. 3. Scheme of an arrangement of three-phase winding on external side of a case of a melting bath or converter

Fig. 2 shows magnetic field penetrating a brick with finite wall width. These bricks are used in converter walls or in a melting bath in the metallurgical furnace. Apparently at vertical position of a brick the magnetic disk does not fall at all under action of gravity, it is kept with the force of magnetic attraction. This means that magnetic field possesses significant penetrating capacity through a brick.

In Fig. 3 the scheme of an arrangement of external windings around a case of a melting unit is shown. This arrangement of winding generates alternative rotating magnetic field. Thus we suggest a new application of rotating magnetic field, which is used widely in three-phase windings r of electromagnetic motors - [5-7]. The vector of magnetic induction B = f(t) rotates around an axis O with the fixed frequency ω.

Resultant magnetic field is rotating because magnetic field is generated in three windings 1, 2, 3 with phase shift of 120 degrees – [5-7]

^B 1 二 ^B m ^sin ① t,

B 2 = B_msmWt - 120 o ),                                                       (7)

B3 = Bmsingt- 240o), where Bm – amplitude of a magnetic field vector, T.

The magnitude of a vector of magnetic induction B does not depend on time and is equal [5-7]

з

в = ]B m .

r                          n                                3c

The effect of rotation of B(t) in space results from — phase shift of projections B x = B m sin 3 t

3B and By = — Bm cos 3 t, so tga =    = tg ① t.

2                 B y

Kinematic viscosity of steelmaking slags changes in the range of v = 3*(10^-6÷10^-4) m²/s and kinematic viscosity of liquid steel changes accordingly in the range of 4·10^-7÷8·10^-7 m²/s [1-3]. For water this parameter is equal to 9·10^-7 m²/s. It appears that liquid metal has low viscosity. r

By penetrating into depth of liquid metal periodically rotating magnetic field B(t) will drag behind itself and cause to rotate some layer of liquid metal. The given method is good in that the magnetic field will rotate layers of liquid metal which adjoin or stick to an internal wall of a converter or a melting bath. Thus layers of molten metal, which are the least involved in mixing before, will be mixed the most.

Fig. 4 is the photo of a constant magnet with which we have conducted experiments using thin metal grit. Distortion of magnetic field by thin layer of a metal sheet was studied. As experiments have ► shown, flat thin iron sheets do not weakennoticeably magnetic field B . Similar experiments were done using the ring magnet in Fig. 2. Thus thin layered metal sheets on external sides of melting baths and converters will not reduce substantially penetration of magnetic field into internal volume of liquid metal.

►

Interaction of an external exciting magnetic field B with the magnetic fields of currents I1 and I2 is shown in Fig. 5. The current I1 is generated when magnetic flux Ф=B∙S increases, and the current I2 is induced when flux decreases. It follows from Faraday’s law of induction for boundary parts of external magnetic field vector, which are shown in Fig. 6, part 1 and 3. In these boundary parts of external rr r magnetic field the doughnut-shaped internal induced field Bp = B]+ B? turns to 90o and “sticks” to a wall of a melting bath 2 (Fig. 5). This phenomenon is similar to Helmholtz vortices observed in fluid

Fig. 4. the source of cylindrical magnetic field

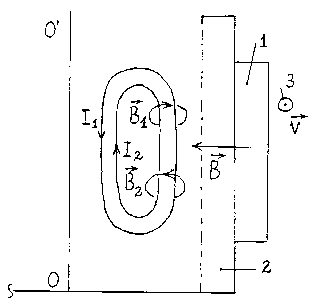
Fig. 5. Interaction scheme of external and of induced internal magnetic fields in a melting bath

r

1 – windings for generation of an external magnetic field B , 2 – wall of melting bath, 3 – direction of rotation rr r of a vector B, Bi, B? - induced magnetic fields, OO' - the axis of a melting bath mechanics. We note that currents I1 and I2 are results of superposition of two currents: I1 = I1,e + I1,i I2 = I2,e + I2,i. The index “e” corresponds to current of free electrons and the index “i” corresponds to current of positive or negative ions.

-

In the central (constant) part of the external magnetic field B (Fig. 6, part 2) the direction of currents ►

I1 and I2 depends on a direction of rotation of the vector B , a designation 3 in Fig. 5. The direction of currents can be determined by the rule of the right hand. Direction of the magnetic volumetric force acting on an element of volume can be defined by the left hand rule. Interaction of the internal induced 二                              — magnetic field vector Bp with the external magnetic field vector B leads to attraction, repulsion or ► cross-sectional (relative to B ) movement of some finite layer of liquid metal. As a result this volume of liquid is involved in mechanical motion and there will be mixing of various layers of liquid metal. The thickness of layer of liquid involved in motion depends on the cross-sectional size of a winding 1 in Fig. 5. Hence rotating magnetic field and volume of liquid metal brought to motion by this field has finite cross-sectional sizes.

The proposed method of intensification of intermixing of liquid metal does not only apply for interaction of С+О. It is possible to apply the method to improve mixing and to increase the rate of chemical reaction of all other impurities in various molten metals and their species.Calculation of mixing rateof impurities plays an important role in the manufacture of semiconductor crystals, which are widely used in electronic industry.

There are particles composed of several atoms and molecules within liquid metal, for example, such as CO, SO, FeC, CaO, NO. There are also large enough particles of slag and structures composed of severalatoms of external impurity. All of these particles and even single atoms in liquid metal can move like Brownian particles. Analysis of the equations describing motion of Brownian particles is vital for the metallurgical branches. In [4, 8, 9] the following equation for calculation of distance traveled by a Brownian particle along X axis is received:

2 kTt x -----

3 яц а

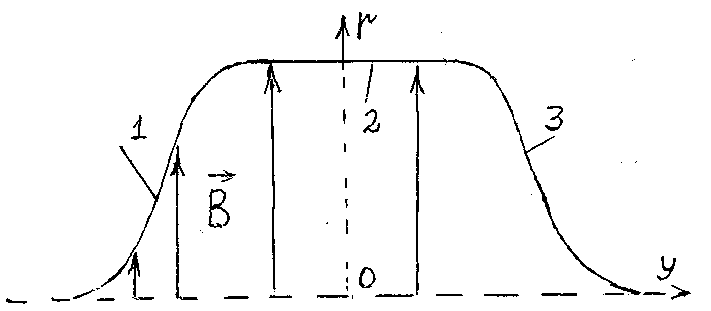
Fig. 6 – Cross-sectional distribution of external magnetic field vector B

1,3 – gradient (boundary) part of the magnetic field, 2 – constant (central) part of the field where µ-dynamic viscosity of liquid, a – particle radius, Т – absolute temperature, t-time.

In literature equation for one-dimensional motion of a Brown particle is presented [4, 8]

d2xdx m—2 = -в『+Fx (t), dt t

Alsoin literature three-dimensional equation is given [9]

m 粤= -В^Г + S dt dt where r = r(x,y,z) - radius-vector of a particle, F (t) = F(t)=(Fx,Fy,Fz) - force casual in magnitude and direction. This force characterizes casual wandering trajectories of particles [4, 8, 9],

B = 6 叩a

r coefficient in the Stocks' equation for drag resistance force Fc = B • v, v — speed of a moving particle. For r simplification purposed equation (12) is multiplied in scalar way on r and after some transformations the scalar equation turns out [9]

mg ( _r 2 卜 в . _d_r 2 = _mv 2 ₊( F ( _t ) , r ) .                                          ₍₁₃₎

dt

Let’s average out the given equation on set of particles and then we will receive m 与(r2 )+ B . * 二 3kT,                                      (14)

dt as mv2/2 = 3kT/2 - according to the theorem of uniform distribution of thermal energy on degrees of freedom and(F (t),r )= 0 - force averaged over time is equal to zero.

The analysis carried out by us has shown that the equation (14) can't be integrated twice ifintegration is done from t = 0 up to the arbitrary time moment t, and then both parts of the result are dividedby a time interval t, as it is done in [9]. In this case after the first integration the equation turns out to be [9]

md 2 B 2

Ir j 丨 * r        3_k^T .

2t dt 2t

This equation can’t be integrated in time any more as a denominator with t is present – [9].

We found that the three-dimensional equation (14) can be integrated successfully twice in time if a technique for integration of the one-dimensional equation (10)used in [8] is implemented.According to this method first we will accept a designation z 二 *Г2. Then (14) will be rewritten as md  B

• z 二 3kT .

..-z +—

2 dt    2

This is ordinary differential equation of the first order – [10]

y‘+p（x）y 二 q（x） whichhas the solution

y

exp

U x \ Tp(x)dx

x

( v

У О + J Q ( v ) exp 〕 P ( u ) du

L dv

xo

I xo       丿

From (16) and (17) we will receive precisely dt в 卜 6BT.

Integrating (18) and using (12) and using initial conditions q = 0 at t=0 from (18) we will easily receive r2 = 6kT = JkTt b 咿

Equation (19) is the solution of a given problem and shows an averaged square of radius-vector of three-dimensional motion of a Brownian particle.The same result can be obtainedfrom the equation (9) if following assumption is made [4,8]

x² = y² = z² .                                                                   (20)

Then the equation (19) follows from the fact that r² = x² + y² + z² [8,9].

Discussion

As is known, metallurgical manufacture is a set of complicated interconnected technologies and processes demanding considerable material inputs. We hope that equal consideration of fundamental and applied sides during the solution of the important scientific and technical problem will lead to increasedprobability of success. Therefore we invite for cooperation all interested foreign partners and colleagues.

Theoretical proof that it is possible to mix liquid metal on the basis of influence of an external rotational magnetic field was given. The magnetic field rotates on a circle similarly to how the magnetic field in a stator of electromagnetic motors and generators rotates. Laboratory experiments have shown that magnetic field can pass through a brick. Numerical calculations which show asymptotic decrease – 575 –

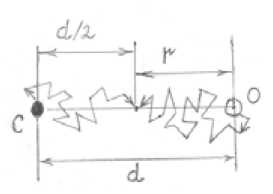
Fig. 7. Scheme ofa Brownian particle movement. Atoms C, O

in concentration of carbon Nc and oxygen No atoms in time are carried out. The model is constructed on an assumption that frequency of interaction of these atoms approximately corresponds to frequency of casual collisions under the theory of effective sections. Free atoms of carbon C and oxygen O in liquid metal don’t lose kinetic energy as a result of potential interactions. Therefore the given model works approximately. Procedure for exact integration of the equation of motion for the Brown particle in three-dimensional case is shown.

Let two particles be within the liquid environment and be at initial time t_ο at distance d from each other. It is possible then to assume that particles are distributed evenly over all liquid volume with step size of d, Fig. 7. Let each particle after some time t to travel to a new position at distance r = d/2. In this case external borders of two volumes will overlap, Fig. 7. Distance r can be calculated with the equation (19) as distance traveled by Brownian particle. From there it is possible to find time t. From time it is possible to calculate average frequency of collisionor impact and from there probabilities of interaction of Brown particles. Equation (19) can be used for calculation of v rel , then model (2-3) will improve.

We stress distinctive and useful points of our conclusion. 1) – the detailed solution of the threedimensional equation (13, 14) has universal value, unlike when the one-dimensional equation (10) is considered only. In three dimensionalcase it is not necessary to do the assumption (20), and this causes projections of a displacement vector to be independent and to have any value. It is easy to pass from _ consideration of r toconsideration of its components x, y, z. In equation (19) numerical coefficients have values: 1/3, 2/3, 1.0; 2) – In this case it is not necessary to search for (or to select empirically) some partial solution of the non-uniform equation – [9]

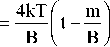
- 8

When using a boundary condition r₀ = 0 it is not necessary to apply a condition that t₀ = Bm <  10

o has very small size – [8]; 3) – Based on probability (frequency) of collisions and on chemical interaction of Brown particles it is possible to solve an inverse problem – to find value of viscosity of the liquid.

Conclusions

• 1.    The hypothesis that rotating variable magnetic field can be used to intensify mixing of molten metal in a melting bath or converter is offered and physically proved.

• 2.    The numerical solution of kinetic equations for casual collisions with use of free-path length of atoms shows that concentration of impurities can decrease to desired level in time interval ranging – 576 –

• 3.    Procedure for exact integration of the equation of motion for the Brownian particle in threedimensional case is shown.

from about several seconds to units of minutes. This shows necessity for improvement of mixing of molten metal with the use of magnetic field, which can also increase efficiency of the technological process.