Абстрактная модель искусственной иммунной сети на основе комитета классификаторов и ее использование для распознавания образов клавиатурного почерка

Один из основных мировых трендов на сегодняшний день связан с развитием технологий искусственного интеллекта (ИИ). Под этим термином подразумевается способность программ выполнять задачи, которые считаются прерогативой человека – классификация, кластеризация, регрессия (аппроксимация функций, прогнозирование временных рядов). Важнейшим свойством для ИИ является возможность быстрого и устойчивого обучения на малом числе примеров , что означает способность ИИ обрабатывать большие объемы данных, а также формировать достоверные решения и делать высокоточные предсказания, даже если обучающая выборка ограничена в объеме и не в полной мере репрезентативна .

Для решения задач из области ИИ существует множество свободно распространяемых программных продуктов (TensorFlow, Keras, Apache MXNet, ONNX, Chainer, Deeplearning4j, Theano и др), позволяющих сторонним разработчикам использовать методы машинного обучения при создании интеллектуальных приложений. Большинство библиотек машинного обучения базируется на многослойных искусственных нейронных сетях (ИНС). Идеи использования «глубоких» нейросетевых архитектур активно популяризуются, в том числе крупными корпорациями (Google, NVidia, Intel, Microsoft). Во многих случаях эти идеи доведены до эффективных практических решений. Тем не менее, этот аппарат имеет недостатки [1], в частности:

– на небольших выборках итерационные алгоритмы обучения проявляют неустойчивость (склонность к переобучению, падение точности при незначительных изменениях параметров ИНС);

– для настройки многослойных сетей требуется огромная база примеров (десятки, сотни тысяч);

– обучение глубоких нейронных сетей не может быть полностью автоматизировано и всегда ведется под контролем человека (инженер-исследователь вынужден подбирать слишком много параметров, влияющих на структур у нейронной сети и алгоритм обучения, что создает большие трудозатраты);

– известные теоремы о представимости функций в виде ИНС и о сходимости процедур обучения градиентным спуском не дают четкой информации о составлении оптимальной конфигурации ИНС под заданную задачу или обучающую выборку;

– существующие алгоритмы обучения в той или иной степени подвержены проблемам переобучения, затухания градиентов, попадания в локальные минимумы поверхности ошибки, параличей сети.

В настоящей работе рассматривается альтернативный биоинспирированный подход, лишенный указанных недостатков, который может применяться при ма- лых объемах и низкой репрезентативности обучающих выборок. Предложены абстрактная модель искусственной иммунной сети (ИИС) на базе комитета классификаторов и устойчивые алгоритмы ее обучения (с учителем и с подкреплением) для задач классификации.

В работе 2005 года [2] описаны проблемы аппарата ИИС, к которым относится его слабая теоретиза-ция (недостаток строгих доказательств работоспособности, сходимости алгоритмов обучения). Эта проблема остается актуальной в 2020 году [3, 4], хотя работы по расширению доказательной базы ведутся [5]. Настоящее исследование апеллирует к хорошо зарекомендовавшим себя методам построения и обучения ансамблей моделей [6] для усиления формально-теоретической основы предлагаемых решений.

В качестве предметной области для демонстрации эффективности разработанных модели и алгоритмов выбрана задача построения метода биометрической аутентификации субъектов по клавиатурному почерку (индивидуальным особенностям ввода пароля на клавиатуре или мобильном устройстве). Данная задача актуальна в контексте проблем информационной безопасности и относится к трудноразрешимым.

Научная задача и достигнутые ранее результаты

При биометрической аутентификации выполняется сравнение «один к одному» предъявляемого образа и эталона определенного субъекта. Для каждого пользователя следует обучать отдельный автомат верификации образов, который настраивается с использованием обучающих выборок (рис. 1) «Свой» (примеры, принадлежащие пользователю) и «Чужие» (примеры, не принадлежащие пользователю).

Все данные (Z классов образов¹)

Выборка Чужие

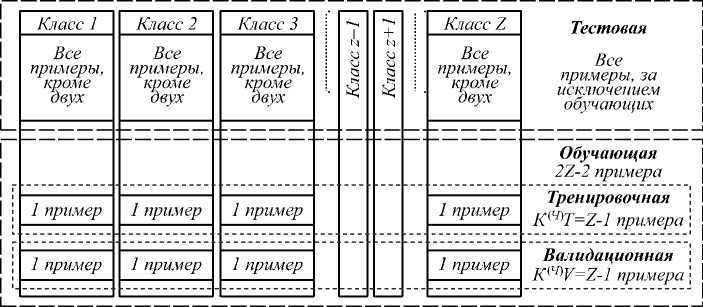
Выборка Свой Класс z Всего Кг примеров

Тестовая №-K

Обучающая K^T+KW примеров

Тренировочная К^(С)Т примера

Валидационная K^tc'V примера

Рис. 1. Структура выборок для испытуемого под номером z, где кт/^(С/Ч) - объем выборки, T- тренировочная, V- валидационная, С - «Свой», Ч - «Чужие», к(С>=кт(С>+к^С>

Объем выборки «Свой» в биометрической системе аутентификации ограничен 10–30 примерами, обучение должно выполняться за короткий промежуток времени (иначе система не будет востребована на практике). Выборка «Чужие» не ограничена в объеме (можно использовать одну большую выборку «Чужих» для обучения всех автоматов аутентификации).

Обычно биометрические данные предварительно подвергаются обработке, в ходе которой из образца данных удаляется незначимая информация и извлекаются биометрические параметры – признаки . При использовании стандартной клавиатуры признаками являются временные задержки нажатий (между нажатиями) клавиш, если для снятия характеристик используется мобильное устройство, то к этим признакам добавляются показатели силы нажатия на экран и площадь соприкосновения пальца с экраном. В настоящей работе использовались базы образов клавиатурного почерка, представленных векторами признаков и не требующие дополнительной обработки.

Признаки клавиатурного почерка малоинформативны и меняются в зависимости от времени суток и психофизиологического состояния человека [7]. Как следствие, обучающая выборка «Свой» оказывается нерепрезентативной. Проблема репрезентативности для выборки «Чужие» остро не стоит.

Вероятность «ложного допуска Чужого» (FAR) должна быть ничтожно мала, а вероятность «ложного отказа Своему» (FRR) может быть выше (приемлемый уровень – 10–25 % ошибок). Показатели FRR и FAR взаимозависимы, их соотношение определяет пороговый коэффициент, с помощью которого их можно балансировать. Сравнение методов распознавания иногда осуществляется по средней точности (Mean Accuracy, далее MAC= 1 –(FRR+FAR)/2) – соотношению верных решений и количества опытов. Однако чаще используется коэффициент равной вероятности ошибок EER, когда выполняется условие: EER ≈ FAR ≈ FRR ≈ 1 – MAC. Для этого при тестировании строятся характеристические кривые (ROC-кривые), отображающие взаимную зависимость FRR, FAR и порогового коэффициента. Если MAC принимает низкие значения, например, менее 0,9 (или EER> 0,1), то, настроив систему на FAR= 0,0001, мы можем получить 1 ≥ FRR> 0,5 (более 50% «ложных отказов»). Все зависит от характера ROC-кривых.

Достигнутые ранее результаты (табл. 1) говорят о том, что найти решение этой задачи затруднительно, в том числе в нейросетевом логическом базисе. Для использования потенциала методов «глубокого» обучения требуется большой объем обучающей выборки, не реализуемый на практике (320 примеров на человека). Рассматриваемая научная задача хорошо иллюстрирует ограниченность применимости ИНС.

Табл. 1. Достигнутые показатели надежности для методов классификации субъектов по клавиатурному почерку

Сведения о методе классификации	Объем обучающей выборки «Свой» ĸ(С) (на человека)	Описание базы данных образов	EER	MAC
			в долях / вероятностях
Рекуррентные ИНС (2 LSTM блока, оптимизатор Adam) [8]		Б1 (n=31) : 51 испытуемый (по 400 примеров ввода пароля ".tie5Roanl" на клавиатуре, всего 20400 образов), данные получены за 6 месяцев (испытуемые вводили по 50 примеров через определенный период времени) [10]	0,227	0,773
Рекуррентные ИНС (3 GRU блока, оптимизатор Adam) [8]			0,15	0,85
Рекуррентные ИНС (3 LSTM блока, оптимизатор Adam) [8]			0,219	0,781
Малые и «глубокие» сверточные ИНС с предобучением и без [9]	200–300			≤ 0,925
«Манхэттенская» масштабируемая метрика [10]	200 примеров		0,096	0,904
Меры Махаланобиса и ближайшего соседа [10]	200 примеров		0,10	0,9
Статистическая техника (на базе z-оценки) [10]	200 примеров		0,102	0,898
Машина опорных векторов (SVM) [10]	200 примеров		0,102	0,898
Автоассоциативный многослойный персептрон [10]	200 примеров		0,161	0,839
Мера Евклида [10]	200 примеров		0,215	0,785
Нечеткая логика [10]	200 примеров		0,221	0,779
Метод k-ближайших соседей (k-NN) [10]	200 примеров		0,372	0,628
«Глубокая» ИНС, оптимизатор Nadam [11]	320 примеров			0,92
SVM [11]	320 примеров			0,7115
Наивный Байес [12]	34 примера	Б2 (n=71) : 42 испытуемых (по 51 примеру ввода ".tie5Roanl" на планшете или смартфоне), данные временных задержек, силы нажатия, площади касания [12]		0,7893
Сети Байеса [12]	34 примера			0,9194
C4.5 (J48) [12]	34 примера			0,6902
k-NN [12]	34 примера			0,7298
SVM [12]	34 примера			0,8833
Случайный лес [12]	34 примера			0,9304
Многослойный персептрон [12]	34 примера			0,8626
Мера Евклида [12]	34 примера		0,157	0,843
«Манхэттенская» метрика [12]	34 примера		0,129	0,871
Мера Махаланобиса [12]	34 примера		0,166	0,834

Архитектура клеток иммунной сети

Прежде всего, отметим, что ИИС (как и ИНС) – крайне упрощенная конструкция, которая не подразумевает строгого соответствия своему биологическому прототипу. Искусственные иммунные системы (сети) в компьютерных науках принято рассматривать как семейство алгоритмов [4], основанных на соответствующих теориях о естественной иммунной системе (ЕИС): дендритных клеток, негативного отбора, клональной селекции (положительного отбора), сетевых алгоритмов (последние чаще всего называют иммунными сетями, а не системами, далее все типы иммунных моделей будем называть ИИС).

Иммунная система содержит множество клеток (макрофаги, дендритные клетки, лимфоциты), которые обладают способностью обнаруживать и удалять чужеродные организмы (антигены). Назовем все такие клетки детекторами [4] – вычислительными элементами, способными анализировать распознаваемый образ либо его отдельные фрагменты и реагировать на него пропорционально тому, насколько этот образ соответствует антигену. Шкала реакций задана на интервале действитель- ных чисел [0; 1], где 0 – полная уверенность в том, что клетка принадлежит организму (гипотеза «Свой»), а 1 – полная уверенность в обратном (гипотеза «Чужой»). Силу взаимодействия между клетками ИИС и антигеном также называют аффинностью. Каждый детектор следует рассматривать как бинарный классификатор, состоящий из нескольких функций, последовательно применяющихся к биометрическому образу. Образ представляет собой вектор признаков фиксированной длины ā = {a1, a2,…, an}, где n – количество признаков, которое должно присутствовать в образе. В общем виде получ ение реакции i-го детектора на входной образ ā можно описать формулой (1):

u = Ф х ( у ' = ф ( у = f ( а = R ( a , V ), ^Г, ® , - ),T i ) ) , (1)

опишем функции детектора и их параметры:

• 1)    ᾱ = R ( ā, Ψ ) – функция-рецептор, предоставляющая интерфейс взаимодействия для детектора и антигена. Данная функция извлекает ŋ из n признаков, содержащихся в ā , Ψ – множество номеров признаков из ā , которые должен анализировать -й детектор. Вектор ᾱ = { a 1 , a 2 ,…, a ŋ } является подмножеством ā с собственной сквозной нумерацией элементов;

  2) y = f x (a, g , 0 i ) - функция-ядро детектора, параметрический функционал, который вычисляет близость вектора а к эталону класса образов «Свой»; x - тип функционала (ниже даны формулы (2 -11)); g - вектор параметров функционала, которые влияют на характер вычислений; 0 i = {р. 1 , р 2 , ^, р ₉ , О 1 , 0 2 , ^, о ₉ }, р j и a j - статистические оценки параметров распределения значений j -го признака из вектора а. Данные из множества 0 i рассчитываются на основании нескольких случайных примеров из обучающей выборки (далее фолд ). В настоящей работе для построения ядер детекторов применялись следующие функционалы: мера Минковского (2), разные вариации меры Байеса-Минковского (3 - 5), «наивный Байес» в дифференциальной (6) и интегральной форме (7), параметрические критерии (8 -11). Разные функционалы образуют различные виды детекторов, которые дают слабо коррелированные решения относительно друг друга. Из любого функционала можно получить разные меры близости за счет изменения параметров g . Часть представленных мер близости применялась в работе [13] при построении «гибких» нейронных сетей.

  
  

  более точную оценку близости при разных уровнях взаимной коррелированности признаков. Желательно подбирать признаки Y i таким образом, чтобы коэффициенты парной корреляции г-д были близки по значению [1], причем для меры Минковского r -,_t <0,5, а для меры Байеса-Минковского r -,_t > 0,5.

  
  

  n

  ^f ; ( « . g = ^{ g 1 , g 2 ^,■■■^, g n ^}, ® - ) = П P g, ^{( a} - , P j , ^a - ), ⁽⁶⁾ j =1

  ⁿ

  ^f ; ( « . g = ^{ g 1 , g 2 ^,■■■^, g n ^}, ©J = П P g - ^{( a} - , P - , - ⁽⁷⁾

  - =1

  где P _g ( a , p, a) и p _g ( a , p, a) - значение функции распределения и плотности вероятности соответственно, с учетом значения признака a - и его параметров распределения (р - и a - ) для класса «Свой». Реализация этих функций зависит от закона распределения, который определяется параметром g - . В настоящей работе использовалось три вида закона распределения:

  - нормальный ( g - = 1):

  
  

  P 1 ( a - , p - -, a - ) =

  
  

  f Ka, ^g = ^{ g ^}, ©О =

  
  

  f : ( « , g = { g }, © - ) = L

  j =1

  
  

  ⁽ p - ^- a j ) ^a -

  
  

  ( p t - a t )

  
  

  ^g

  
  

  _-

  
  

  ⁽ p - ^- a j )

  
  

  ^g

  
  
  
  

  P ( a - , p - -, a - ) =

  
  

  e

  a j V2n

  
  

  a j V2n

  
  

  a t

  
  

  ^a -

  
  

  , (3)

  
  

  ( a j —P j ) 2a?

  ^,

  
  

  a

  J ^e

  p - ^{- 5 a} -

  
  
  
  

  (9 на '

  ^{2 a} - ² d 9 ,

  
  

  где p и a - математическое ожидание и среднеквадратичное отклонение -го признака;

  - логнормальный ( g - = 2):

  
  

  ^f l ( a . ^g = ^{ g ^} ® / ) = ^g L

  
  

  ( p t - a t )

  
  

  (-a - ) ^a

  
  

  p 2 ( a - , p - -, a - )

  
  

  e

  aj-a j V2n

  
  

  ( Ln (9)-p - ) ² 2a - ²

  
  

  ^f i ^{( a} , ^g = ^{ g ^}, ® / ) =

  
  

  v at a / gg L----

  \ - =1 ^a t ^a -

  
  

  n

  
  

  ^g

  
  

  ,

  
  
  
  

  1             a j      _ ^{( Ln ( 9 ) -} p - ^{) 2}

  P i ( a - , p - , a - ) =------- [ e    ^{2a - 2} d 9 ,

  a j a j4 ² n p-5a₁

  
  

  где a - - значение j -го признака, p j и a j - математическое ожидание и среднеквадратичное отклонение j -го признака, g - степенной коэффициент, g е [0,01; 100]. Мера Минковского ориентирована на нахождение расстояния в пространстве признаков с низким уровнем взаимной корреляционной зависимости r -,_t < 0,5 (где r -,_t - коэффициент парной корреляции Пирсона между j -м и t -м признаками). Когда признаки независимы ( г-дК 0), оптимальное значение степенного коэффициента g = 2 (мы имеем меру Пирсона, а при a j =1 - меру Евклида). При g =1 мы получаем меру «городских кварталов», при g ^ю мера Минковского стремится к мере Чебышева. Если пространство признаков искривлено из-за корреляционных связей между признаками (0 >  r -,_t < 0,5), то изменение g позволит выполнять более точное вычисление расстояний Минковского. Мера Байеса-Минковского, напротив, ориентирована на обработку сильно зависимых признаков ( г-д >0,5). Изменение g позволяет давать

  
  

  где p и a - параметр масштаба и формы;

  - закон распределения Лапласа ( g - = 3):

  
  

  a.

  p 3 ( a - , p - , a - ) = 2^ e ^{-a -} i a , ^{-p -} i ,

  
  

  P 3 ( a - , p - , a - )

  
  

  0,5 e ^a - ^{( a} - ^-p-\ a j

  j

  1 - 0,5 e ^-a - ⁽ a - -^ j ) , a - >p -’

  
  

  где p и a - коэффициенты сдвига и масштаба.

  Параметры клавиатурного почерка, а также большинство других биометрических признаков имеют законы распределения, близкие к указанным выше [14]. При решении иных задач распознавания образов перечень законов распределения может быть расширен.

  
  

  ^f - ( a , '^g = ^{ g ^}, © - Э =

  = J g /l P 1 ( 9 , p a , a _a ) - P 1 ( v ,0,1) | ^g ■ d 9 ,

  -5

  
  
  
  

f 8 ^{( a} , g = ^{ g ^}, ® i ) =

= J ^g^ p i ( d , Ц a , Q a ) - P 1 ( 9 ,0,1) | g ■ d 9 ,

-5

^f 9 ^{( a} , g = ^{ g^} , ® i ) =

= J g/|P(9, Ц a , Qa) ■ (1 - 71(9,0,1)) |g ■ d9, f1o(a, .g = {g}, ®i) =

= J Vl P 1 ( 9 , Ц a , Q a ) ■ P 1 ( 9 ,0,1) | g ■ d 9 .

-5

Последняя группа функционалов (8 – 11) представляет собой модификации критериев согласия, используемых для сравнения эмпирически наблюдаемой функции распределения (плотности вероятности) для величины å с теоретической (эталонной), при этом предполагается, что закон распределения близок к нормальному, å – нормированное значение любого признака, μ å и σ å – математическое ожидание и среднеквадратичное отклонение. Нормирование (приведение всех a j к единой случайной величине å ) производится по данным из Θ i в соответствии с формулой:

aj-µj a=

σ j .

Параметры распределения å для класса «Свой» должны принимать стандартные значения (μ å ≈ 0 и σ å ≈ 1), для образов «Чужих» будут наблюдаться значительные отклонения (μ å ≠ 0 и/или σ å > 1). Предложенные функционалы (8 – 11) обобщают критерии Джини, среднего геометрического вероятности и плотности вероятности, рассмотренные в работах [15, 16];

• 3)    y' = φ( y , T i ) – функция нормирования откликов y относительно порога T i , который вычисляется в процессе настройки i -го детектора. Функция нормирования может иметь 2 реализации:

φ(y, Ti) = y / Ti, если y – это расстояние от ᾱ до эталона класса «Свой» (чем меньше, тем ближе), тогда Ti – это максимальное значение функции-ядра i-го детектора, при поступлении на его вход обучающих образов «Свой», либо:

φ(y, Ti) = Ti / y, если y – это вероятность того, что ᾱ принадлежит классу «Свой», тогда Ti – это минимальное значение функции-ядра i-го детектора, при поступлении на его вход обучающих образов «Свой». Физический смысл y (расстояние или вероятность) зависит от функции-ядра соответствующего детектора (например, для меры Евклида требуется использовать первый вариант, а для «наивного Байеса» – второй);

• 4)    u i = ϕ χ ( y' i ) – функция активации, дополнительный нелинейный элемент детектора, который определяет особенности реагирования на антиген. Функция активации также необходима, чтобы при-

• вести отклик детектора к области значений [0; 1]. В настоящей работе применялись сигмоиды (арктангенс, гиперболический тангенс и др.). В качестве функций активации имеет смысл использовать либо наиболее быструю из сигмоидальных, либо применять функции, которые дают как можно более отличающиеся результаты, чтобы создавать детекторы с низкой коррелированностью решений на базе однотипных мер близости (в целом x в большей степени влияет на характер преобразований (1) детектора, чем χ).

Одной из теоретических проблем аппарата ИИС является слабая обоснованность используемых мер близости [2] (чаще всего применяется мера Евклида). Согласно теореме «об отсутствии бесплатных завтраков» (No Free Lunch) ни одна мера близости не может быть оптимальной для всего множества задач распознавания образов. Поэтому в настоящей работе каждый детектор определяет аффинность уникальным способом, а состав детекторов «подстраивается» под задачу и определяется в процессе обучения ИИС.

Искусственная иммунная сеть как система двух комитетов классификаторов

Предлагается разделить детекторы на две группы: врожденный и приобретенный иммунитет, и рассматривать их как два комитета (ансамбля) слабых классификаторов, обучаемых при помощи разных алгоритмов. Коллективное решение комитета из N детекторов может быть вычислено как среднее частных решений:

u = ф ( D * = { D * ,... dN}, a ) =

NN

= ¹ ⋅ϕ ( D ^* , a ) = ¹ ⋅ u.

N ^∑ i=1 ⁱ N ^∑ i=1 ⁱ

Врожденный иммунитет (ВИ) передается посредством генов, органы иммунной системы формируются еще при эмбриональном развитии. У эмбрионов B-лимфоциты образуются в печени и костном мозге. В предлагаемой модели костный мозг является местом пребывания иммунокомпетентных детекторов, параметры и состав которых определяются в ходе эмбрионального (и постэмбрионального) развития. Так, ВИ формируется в процессе итерационного обучения ИИС с использованием тренировочной и валидацион-ной выборок (рис. 2). Последняя используется для промежуточной оценки надежности решений ИИС при смене поколения детекторов (схожие практики применяются при обучении ИНС). Обе выборки являются непересекающимися подмножествами обучающей выборки (рис. 1).

Приобретённый иммунитет (ПИ) развивается с течением жизни и определяет способность организма обезвреживать специфические антигены, которые попадали в организм ранее. В формировании ПИ участ- вует тимус – орган, в котором происходит созревание и обучение T-лимфоцитов. В предложенной модели тимус осуществляет настройку и отбор иммунокомпетентных детекторов, используя валидационную выборку. Адаптивный иммунный ответ приводит к появлению иммунологических клеток памяти (представленных в ИИС детекторами), которые долгое время пребывают в «спящем состоянии» до повторной встречи с тем же антигеном. В разработанной модели ИИС приобретенный иммунитет формируется в процессе функционирования ИИС. Если решение об отнесении образа к категории «Свой» или «Чужой» является неоднозначным, могут генерироваться новые иммунокомпетентные детекторы.

Генератор детекторов

Генерация I детекторов ^L

J Генерация

J детекторов

КОСТНЫЙ МОЗГ осуществляет обучение ИИС с учителем

• 1.    Поиск идентичных детекторов врождённого иммунитета. ’

• 2,    Настройку детекторов (с использован нем образов из тренировочной выборки).

• 3.    Оценку силы детекторов' [реакций на образы «Свой» и «Чужой» из валида-циднной выборки).

• 4.    Дифференцировку детекторов ' по силе.

• 5.    Отбор детекторов для нового поколения и архивацию поколений.

Идентичные и слабые детекторы

Идентичные детекторы

ТИМУС участвует в обучении ИИС с учителем:

Ч. Поиск детекторов, идентичных с уже существующими.

2. Настройку детекторов (с использованием образов из тренировочной выборки).

Новые детекторы

МЕХАНИЗМ ОБУЧЕНИЯ

Решение принято: авторизация либо отклонение доступа

{антиген....... собственная клетка)

Детекторы, которые дали /^

неопределённое решение I।

1  Распознавание|

|     антигена।

1I

БЕЗ УЧИТЕЛЯ

Продолжается, пока не будет принято более определённое коллективное решение детекторов

Детекторы врождённого иммунитета

। Распознавание । антигена ।

Детекторы приобретённого иммунитета

Детекторы, кото* рые склоняются к гипотезе «Свой» или «Чужой»

Клетки памяти

" Сигнал о ^

1 неизвестном г | антигене |

Решение неопределённо: активация приобретённого иммунитета

Рис. 2. Функциональная схема ИИС

Идея объединения классификаторов в комитет основана на теореме Кондорсе, которая утверждает: если мнения экспертов независимы и вероятность правильного решения каждого из них больше 0,5, то с увеличением количества экспертов вероятность правильного решения комитета экспертов возрастает и стремится к единице. Причем чем выше вероятность верного решения для каждого эксперта в отдельности, тем выше вероятность верного решения комитета. Отметим, что решение любого детектора можно инвертировать, чтобы преодолеть барьер Кондорсе в 0,5 (известны также доказательства других теорем [17], позволяющих обойти барьер Кондорсе).

Однако на практике решения классификаторов, играющих роль экспертов, в той или иной мере кор-релированы. Чем ниже коррелированность решающих правил, тем более ощутим положительный эффект при их комплексировании. Таким образом, имеются следующие гиперпараметры , которые влияют на эффективность комитета детекторов:

– N – количество детекторов;

– RD – матрица коэффициентов корреляции Пирсона r(ūi, ūl) между решениями всех возможных пар де- текторов, где ūi – вектор реакций i-го детектора на примеры образов «Чужих» из тренировочной или валидационной выборки;

– ∆ u – сила детекторов, их способность давать как можно более высокие показатели разницы средних уровней реакции на образы «Свой» и «Чужой» (12):

∆ u = μ u ^{( Ч )} – μ u ^{( С )} , μ u ^{( Ч )} > μ u ^{( С )} .                        (12)

В рамках предыдущих исследований [18] была апробирована стратегия снижения уровня коррелиро-ванности решений детекторов, которая оказалась недостаточно продуктивной. Процедура оценки показателей r(ūi, ūl) и дифференциации по ним детекторов оказалась ресурсоемкой. Кроме того, не наблюдалось сходимости алгоритма настройки ИИС. Процесс обучения был слишком длительным и не всегда приводил к ожидаемому результату (не всегда удавалось найти N детекторов с заданным минимальным уровнем взаимной коррелированности решений). По этой причине в настоящей работе выбрана стратегия повышения силы детекторов при условии, что они не должны быть идентичными. При появлении в ИИС идентичных или слабых детекторов происходит апоптоз – процесс программируемой клеточной гибели для уничтожения дефектных клеток (рис. 2).

Необходимо, чтобы решения всех детекторов врожденного и приобретенного иммунитета не являлись полностью коррелированными. Поэтому после генерации детектора должна осуществляться проверка идентичности параметров нового детектора и уже существующих. При обнаружении «двойника» его следует удалить и сгенерировать детектор снова. При этом значения параметров ğ можно считать равными, когда они отличаются менее чем на 10 ^–1 . Конечно, решения детекторов будут в той или иной степени коррелированы (но не на 100%). Чем сильней различаются параметры D i и D l , тем менее коррелированы решения i -го и l -го детекторов.

Генерация и настройка детекторов

Детектор можно описать множеством параметров D i = {Ψ i , ğ, x , χ }. Сгенерировать детектор означает сгенерировать данные параметры. Приведем псевдокод функции генерации детектора:

method GenerateDetector(RF)

// RF – матрица парных коэффициентов корреляции // между признаками

// random( min ; max ) – генерация случайного числа

Ŋ = random(2; n /2)

r max =random(0,1; 1)

if r max >0,5 then r min = random(0; r max ) else r min = random(0,5; r max )

// Выбрать признаки с уровнем взаимной

// корреляции более r min , но менее r max

Ψ i = GetFeatures( r min ; r max ; RF)

// Если признаков с заданным уровнем корреляции

// нет, сгенерировать номера признаков снова if Length(Ψi) < ŋ go to begin

// Выбор меры близости (Мера Минковского не

// подходит для обработки сильно коррелированных

// признаков, а Байеса-Минковского – для слабо

// коррелированных)

if r max > 0,5 then x =random(2; 10)

else x = random(5; 11)

if x = 11 then x = 1

else if 5 ≤ x ≤ 6 then for j from 1 to ŋ do gj = random(1; 3) end else g = random(0,01; 100)

// Выбрать случайную функцию активации

Χ = GetRandomActivationFunction( )

D i = {Ψ i , ğ, x , χ }

// Если новый детектор идентичен одному из

// детекторов ВИ или ПИ, то сгенерировать заново if IsIdenticalToExisting(Di)=true then

D i = GenerateDetector(RF)

return D i

В разработанной ИИС реализуется идея случайных подпространств признаков, но в отличие от алгоритма «случайный лес» Ψi задается с учетом корреляции между признаками. Этот прием называется симметризацией корреляционных связей [19].

Другая идея, которая реализована при генерации детекторов, заключается в объединении разнородных случайных классификаторов (например, описывая признак разными законами распределения, можно получить несколько «наивных» классификаторов Байеса, решения которых не полностью коррелированы). Примером подобной техники является нейросетевое обобщение множества различных критериев [15].

Настройка детектора связана с вычислением порога T i и эталонных описаний признаков Θ i (μ j и σ j ).

Настроенный детектор можно обозначить как D ^*i = {Ψ i , ğ, x , χ , Θ i , T i }, а функцию (1) – как ϕ( D ^*i ).

Алгоритм обучения иммунной сети с учителем (формирование врожденного иммунитета)

Известны следующие базовые методы и подходы для обучения ансамблей моделей:

• 1.    Бэггинг (bootstrap aggregating) – метаалгоритм композиционного обучения машин, основная идея которого заключается в обучении базовых (слабых) классификаторов на разных подмножествах обучающей выборки. Базовые классификаторы могут быть идентичными или иметь разные архитектуры. Бэггинг уменьшает дисперсию голосов базовых классификаторов и помогает избежать переобучения. Принцип работы бэггинга схож с принципами работы метода случайных классификаторов, а также методов накопления сигналов при их обнаружении и заключается в повышении отношения сигнал / шум.

• 2.    Бустинг (boosting) – семейство алгоритмов машинного обучения, преобразующих слабые обучающие алгоритмы к сильным. Бустинг строит ансамбль путём тренировки каждого нового классификатора, уделяя больше внимания обучению на тех тренировочных примерах, которые предыдущие модели классифицировали ошибочно (например, путем присвоения весов обучающим примерам), и имеет тенденцию к переобучению. Эффективность этого подхода доказана экспериментально и теоретически, что впервые подтверждено для алгоритма AdaBoost [20].

• 3.    Стекинг (stacked generalization) предполагает построение многослойных структур из ансамблей классификаторов, когда выходные данные ансамбля первого слоя воспринимаются ансамблем второго слоя как входные данные (метапризнаки). При использовании стекинга увеличивается необходимый для обучения объем выборки, так как для корректного обучения метамодели каждый слой требуется настраивать на разных тренировочных примерах.

При разработке итерационного алгоритма обучения ИИС были учтены первые два подхода (бэггинг позволяет компенсировать склонность к переобучению бустинга), но от стекинга решено отказаться, учитывая малый объем обучающей выборки, а также тот факт, что ИИС не образует конструкций в виде слоев.

В разработанном алгоритме на каждой итерации происходит генерация новой популяции детекторов, которые настраиваются с учетом нескольких случайных тренировочных примеров (бэггинг), и выполняется промежуточная оценка их эффективности как на тренировочной, так и на валидационной выборке (рис. 3), слабые детекторы уничтожаются (апоптоз), в результате появляется новое поколение иммунокомпетентных (более эффективных) детекторов. Мерой эффективности (обученности) детекторов можно считать ∆ u (12) . По результатам последней валидации вычисляются оценки μ u^(С) и μ u^(Ч) для коллективного решения детекторов ВИ. Эти параметры используются для построения интервала неопределенности решения (ИНР) [μ u^(С) ; μ u^(Ч) ]. ИНР является частью механизма подкрепления при дообучении ИИС в процессе функционирования. Этот механизм активируется при формировании ПИ, что будет изложено в следующем параграфе.

На каждой итерации обучения синтезируются новые образы «Чужих» (рис. 3) путем скрещивания тренировочных примеров, которые хуже всего классифицируются детекторами ВИ (далее сильные «Чужие»). Сильные «Чужие» дают наименьшую среднюю совокупную реакцию детекторов ü . Скрещивание образов ā k и ā m происходит с помощью линейной интерполяции значений признаков:

a c ,j =

Csyn + 1 - c c --ak , +---a„ k,j                         m,j syn                       syn где Csyn – количество синтетических примеров, порождаемых парой «сильных Чужих» предыдущего поколения (в настоящей работе Csyn = 1), c – номер синтетического примера, j – номер признака. Этот способ синтеза «Чужих» наиболее эффективен, если значения признаков имеют распределения, близкие к нормальному, на нем основан ГОСТ Р 52633.2-2010, имеющий отношение к тестированию средств высоконадежной биометрической аутентификации.

Синтетические образы, получаемые путем скрещивания сильных «Чужих», добавляются в тренировочную выборку. Детекторы нового поколения настраиваются с учетом синтезированных примеров, что позволяет следующему поколению детекторов лучше классифицировать образы «Чужих», наиболее близких к образам «Свой». Таким образом, ИИС одновременно «учится» создавать образы более сильных «Чужих» и распознавать их. Предложенный механизм размножения сильных «Чужих» при обучении является еще одной вариацией бустинга.

На скорость и эффективность алгоритма обучения, представленного на рис. 3, более всего влияют следующие основные параметры:

I ВИ – количество итераций обучения (валидаций);

N ВИ – количество детекторов ВИ;

Q – количество сильных «Чужих» (на каждой итерации генерируется C syn ^ Q ( Q – 1)/2 примеров).

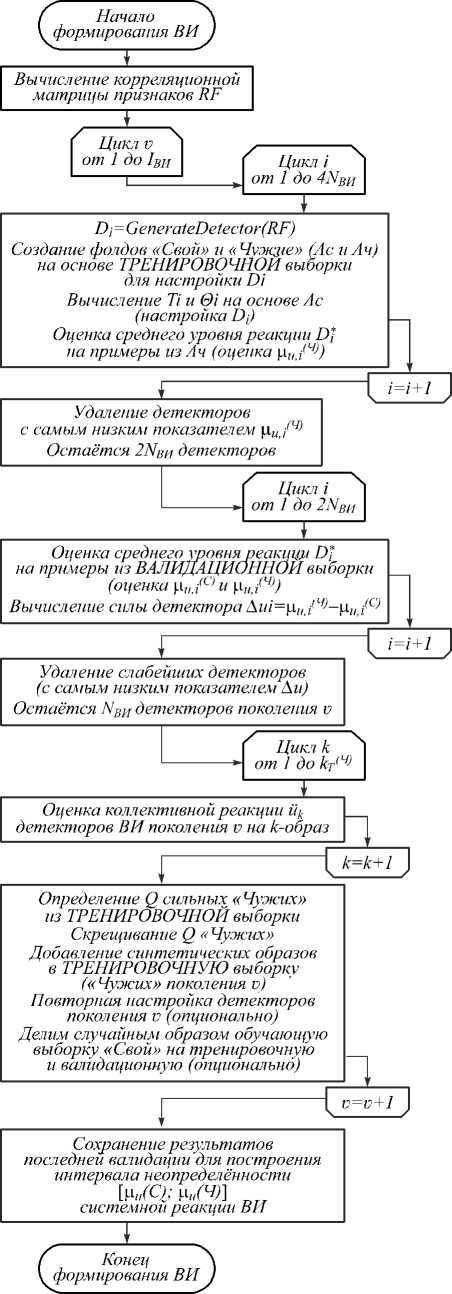
Рис. 3. Алгоритм формирования ВИ

Также параметрами алгоритма являются объемы тренировочной ( ĸ T ) и валидационной выборок ( ĸ V ), размеры фолдов «Свой» ( ĸ F^(С) ) и «Чужой» ( ĸ F^(Ч) ). В настоящем исследовании размер фолдов определялся из соотношения ĸ F^(Ч) = ĸ T^(Ч) /3, ĸ F^(С) = 2^ ĸ T^{(С )} /3. Объем тренировочной выборки «Чужие» и размер фолда «Чужие» не являются фиксированными, а увеличиваются с каждой итерацией обучения при добавлении в тренировочную выборку синтетических примеров . Валидационная выборка всегда остается неизменной.

Алгоритм дообучения иммунной сети с подкреплением (формирование приобретенного иммунитета)

Если обучающая выборка нерепрезентативна, эффективность детекторов ВИ может не соответствовать оценке ∆ u (12), при этом нет гарантий, что плохо настроенные детекторы в действительности преода-левают барьер Кондорсе (для таких детекторов оценки на тестовой выборке должны принимать вид μ u,i^(Ч) < μ u,i^(С) ). Обойти барьер Кондорсе можно, если дать возможность детекторам ПИ голосовать за коллективное решение детекторов ВИ.

Введем следующее правило, основанное на ИНР: при u i >  μ u^(Ч) или u i < μ u,i^(С) решение D ^*i считается определенным, а при μ u^(С) <  u i < μ u^(Ч) решение D ^*i не определено. Если при распознавании образа решение детекторов ВИ считается неопределенным, то активируется механизм ПИ (рис. 4). Генерируются новые детекторы, которые настраиваются на других данных – примерах из валидационной выборки. Для новых детекторов вычисляются реакции u i , но при формировании коллективного решения учитываются голоса только тех детекторов, которые дают определенный ответ (эти детекторы становятся клетками памяти), детекторы ПИ с неопределенным ответом уничтожаются. На скорость и эффективность алгоритма дообучения, представленного на рис. 4, более всего влияют следующие основные параметры:

I ПИ – количество итераций обучения;

N ПИ^(max) – максимальное количество детекторов ПИ (тогда N ПИ – их фактическое количество).

Введение I ПИ позволяет избежать бесконечного цикла дообучения. Детекторы приобретенного иммунитета могут компенсировать недостаток априорных знаний о классах образов «Свой» и «Чужой».

Результаты эксперимента

Для проверки эффективности предложенных модели и алгоритмов использовалось 3 базы клавиатурного почерка: из работ [10] (Б1), [12] (Б2) (см. табл. 1) и собственная база (Б3). Последняя включает 32 человека, каждый из которых 50 раз ввел на клавиатуре фразу «система защиты должна постоянно совершенствоваться» ( n = 63, учтены только попытки безошибочного ввода).

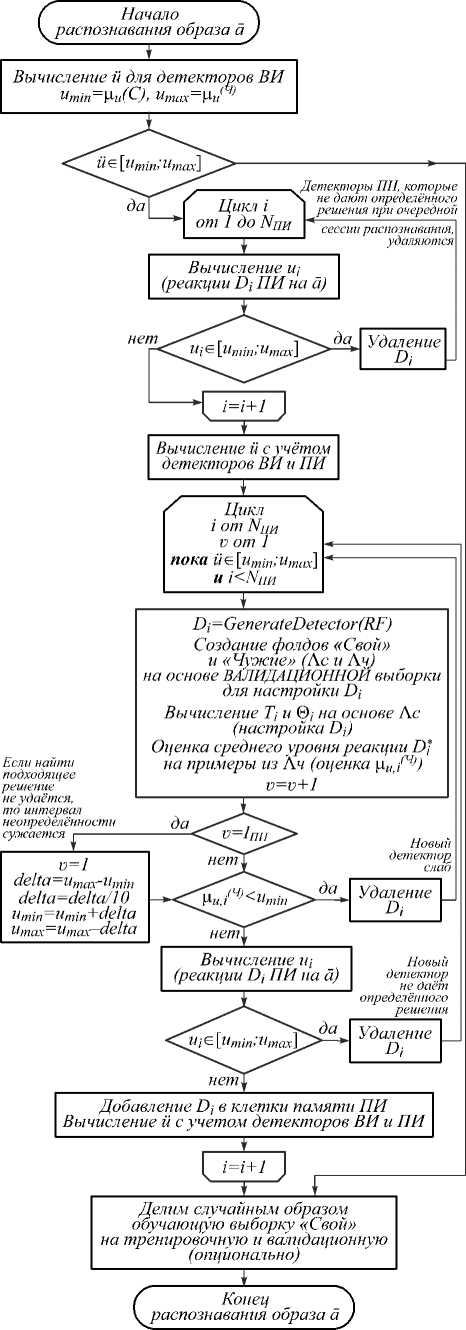
Рис. 4. Алгоритм работы ПИ

Опыты проводились при различном объеме обучающей выборки примеров «Свой»: от ĸ ^(С) =20 до

к ^(С) = 40. Тренировочная к тС и валидационная к^ С выборки примеров «Свой» (подмножества обучающей) перед обучением делились в соотношении: к -С = 2- к^ С . Тренировочная к -Ч и валидационная к^Ч выборки примеров «Чужих» включали по одному примеру от каждого испытуемого из набора данных, кроме примеров «Свой» (рис. 1). Остальные примеры использовались в качестве текстовой выборки. Тестирование проводилось методом перекрёстного сравнения (при расчете FAR образ каждого субъекта сравнивался с эталонами всех остальных субъектов). Таким образом, для каждого испытуемого объем тестовой выборки «Чужих» варьировался в зависимости от набора данных так: Б1 – 19900, Б2 – 1968, Б3 – 1488. Показатели FRR и FAR вычислялись как отношение числа ошибок «ложного отказа» или «ложного доступа» к числу соответствующих опытов. Результаты представлены на рис. 5 и в табл. 2.

Рис. 6 иллюстрирует, как определить EER, а также что FRR и FAR можно балансировать, например FRR=0,193 при FAR=0,0001 (рис. 6 б ).

Надежность решений зависит от того, как была составлена обучающая выборка. Это наглядно видно при тестировании на базе Б1 [10], которая отсортирована по временным меткам. Если выбирать обучающие примеры равномерно (как в [11], где MAC=92,6), то обучающая выборка будет репрезентативной, но если обучать и тестировать систему на образах испытуемого, которые были введены в разные дни (с большим перерывом), то репрезентативность выборки окажется низкой. В этом случае наблюдается более существенная разница в надежности решений для режима ВИ (когда используются детекторы только врожденного иммунитета, т.е. Н _ПИ7^тас) =0) и ВИ+ПИ (когда используются детекторы врожденного и приобретенного иммунитета, т.е. Nm(^max) >0).

EER 0,15

0,1463

----Б1, 2^=25 (нерепрез.)

--Б1, к<с)=40

Б2, #>=21---БЗ, к<с)=24

Б2, к^=27

БЗ, к^=27

0,12

\ 0,1251 --— --_     0,1174           0,1174          0,1174          0.1178

0,1112       0.1234         0И91           ojj73         ()1Пб         о]]б7

0.09

0,0857

0,06

_ 0,0682

0.0*555:

2-0912                                                           ппе7П

^ JTpSeO^JlSM, 0.0839   0,0844  Q.Q833_ q, 0822 0,0824_0Д)339

0^07!9 0 0700 0,0680 0,0690 0,0706  0^717 ~9о7оТ"о?О7О9 0,0722  0 0?00  q

(111603 0,0592 0.0569  0,0564 0,0568 0,0556 0.0531  °’0581

0,0406 0,0390 0.0387

0,0641 00608

0,03

О'—

а)

EER 0,15 V

0,12 -

0,09 -

0,06 -

0,0389

0,0417

0,0358 0.0335 °^5А. 29183._?^.3.64,_0,0353 0,0333

0,0314    0.0319 0,0328 О,О319"“о*О299 0,0316 "o"^)""0,0313......"o*O285

1ви

0,1451

35    300

450	600    750    900   1050	1200  1350	1500	3000
X________	Б1, к^^—25 (нерепрез.) Б1, к(с)=40            -----	Б2,к<с)=21 - ■Б2,к^=27 .....	-БЗ. .....БЗ,	км=24 ' к(с)=27 ,

0,1231 п

0,1369

0,1192 □

0,1078

0,1026 °-

0,1068

0,0870

0,0748

0,0623

0,0810 - у 0906

0,0804 ^.u-vyvo

0.0655

<М186 _о,117О  0.П63    0J154 ____{fi ip6 0Jp}_₅

0 0969 00949   00939

°---о--------- 0,0886   0,0874   0,0882

0,0689 о,О68О 0.0676

0.0752        ----------------------0----

0,0713   0,0674    0,0691

.^0,0502 0,0498 0,0493    0 0482

0,0672

—а— 0,0654 0,0454

0,0670 --В—

0,0687

0.0421

0,0653

----В

0,0682

0,0416

0,03 -

0,0395     0,0393      _{0 0373}   q‘q₃*5......"■■■-.»................_.......

°-0324       0,0288

0,0287

б)                 5       10      20      30      40      50     100     150     200

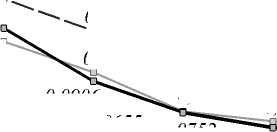
Рис. 5. ROC-кривые, демонстрирующие результаты эксперимента при использовании только врожденного иммунитета (ИпИ^гпа:х> = 0) при Q = 4: Нви = 50 (а), 1ви = 50 (б)

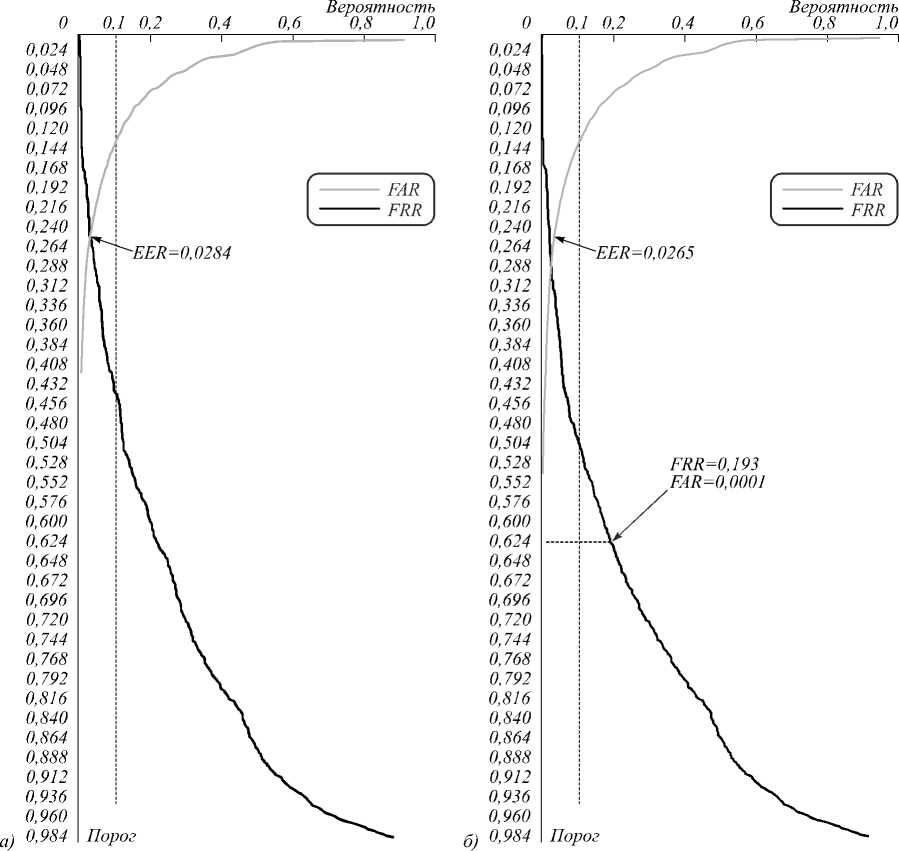
Рис. 6. ROC-кривые, демонстрирующие результаты эксперимента для Б3, при Q = 4, IВИ = 1500, ĸ(С) = 27: а) ВИ (NВИ = 50, NПИ(max) = 0), б) ВИ + ПИ (NВИ = 50, NПИ(max) = 25)

Табл. 2. Сводная таблица основных показателей надежности в зависимости от объема обучающей выборки ĸ(С) и от использования ПИ, при IПИ = 5, Q = 4

База	ĸ(С)	IВИ	NВИ	NПИ(max)	EER
Б1	25	1500	50	0	0,1167
Б1	25	1500	50	50	0,1028
Б1	40	1050	50	0	0,0821
Б1	40	1050	50	25	0,0798
Б2	27	1500	50	0	0,058
Б2	27	1500	50	25	0,0612
Б3	27	1500	50	0	0,0284
Б3	27	1500	50	25	0,0265

Чем дольше обучается ИИС, тем надежнее ее решения, но чем лучше обучена ИИС, тем больше времени требуется, чтобы поднять надежность еще выше (рис. 5а). Процесс обучения является достаточно устойчивым, но при высоких значениях IВИ все-таки наблюдается незначительная склонность к переобучению. При увеличении NВИ (рис. 5б) показатель EER монотонно снижается, темп снижения постепенно ослабляется и почти полностью останавливается, когда решения детекторов ВИ становятся сильно зависимыми (что неизбежно при росте их количества).

Оценка характера влияния других параметров на результаты работы ИИС является темой дальнейших исследований. На данном этапе можно утверждать, что разработанная модель и алгоритмы ее обучения удовлетворяют основным принципам построения ИИС [21], которые применительно к настоящей работе можно переформулировать так:

• 1.    Распределенный характер вычислений и проявление эмерджентности (ИИС может повышать качество решений в процессе функционирования, в отличие от базовых классификаторов, точность распознавания для ИИС выше, чем для каждого классификатора в отдельности).

• 2.    Достаточно устойчивый процесс обучения (склонность к переобучению незначительна при формировании ВИ).

• 3.    Способность ИИС к адаптации, обусловленная двойной пластичностью: структурной и параметрической (меняются параметры и состав детекторов).

• 4.    Взаимодействие – врожденный иммунитет формирует параметры, которые влияют на механизм подкрепления детекторов приобретенного иммунитета.

• 5.    Надежность решений ИИС зависит от объема и чувствительности популяции детекторов.

• 6.    Формирование памяти при помощи механизма приобретенного иммунитета.

Заключение

Предложены модель искусственной иммунной системы и алгоритмы ее обучения с учителем и с подкреплением. Предложенные решения основаны на применении методов математической статистики, ансамблей классификаторов, многомерных функционалов Байеса [1, 19], а также аналогий с теориями о естественной иммунной системе. В настоящей работе не приводится строгих доказательств сходимости предложенных алгоритмов, но даны достоверные свидетельства, доводы и результаты эмпирических исследований, которые говорят об их высокой эффективности. В задаче аутентификации по клавиатурному почерку разработанная ИИС превосходит многослойные ИНС (и другие рассмотренные в работах [8– 12] методы) либо дает сопоставимые с ними показатели ошибок распознавания при гораздо меньшем объеме обучающей выборки (в разы). При этом ИИС легко обучить, достаточно лишь указать параметры N ВИ и N ПИ , напрямую влияющие на объем ИИС и надежность ее решений, а также I ВИ и I ПИ , напрямую влияющие на длительность обучения, время принятия решений и их надежность (обучение является устойчивым независимо от данных параметров).

Хочется подчеркнуть, что в настоящей работе не утверждается превосходство предложенного аппарата над нейронными сетями в общем случае. Это разные инструменты для решения разных задач. Их также можно использовать совместно. Например, извлечение признаков может выполняться при помощи глубокой сверточной нейронной сети (предварительно обученной «сжимать» образ до определенного количества признаков), а распознавание образов – с помощью иммунной модели.

Мощность предложенной модели ИИС связана с количеством вариаций мер близости, используемых в основе детекторов. В рамках будущих исследований целесообразно создать таблицу, в которой будут представлены различные функционалы, их параметры и свойства, чтобы сделать генерацию детекторов более эффективной под конкретную задачу.

Предложенный аппарат столкнулся со следующими проблемами:

• –    детекторы способны работать только с признаками, но не способны анализировать «сырые»

• да нные. Требуется разработать архитектуру детекторов, способных извлекать признаки (по аналогии со сверточными сетями);

• –    разработанная модель не позволяет решать задачи кластеризации и регрессии. Требуется разработать адаптированную для данных задач модель ИИС;

  – в разработанной модели имеется незначительная склонность к переобучению при формировании ВИ (исправить этот недостаток видится возможным, если контролировать коррелированность решений детекторов непосредственно либо изменять гиперпараметры ИИС в зависимости от ИНР). Устойчивость процесса дообучения при формировании ПИ пока мало изучена, что требует дальнейших исследований.

Тем не менее, данные проблемы не являются критическими и могут быть решены. Дальнейшие исследования планируется направить на поиск решений указанных проблем, а также: на оценку влияния параметров Q , N ПИ , I ПИ ; разработку и обоснование механизма мутаций детекторов; применение разработанных положений в других задачах; оптимизацию кода и алгоритмов (с использованием параллельных вычислений) для ускорения обучения.

Работа выполнена при финансовой поддержке РФФИ (грант № 18-37-00399).