Acoustic lightweight pseudo random number generator based on cryptographically secure LFSR

Random numbers defined as “A sequence of integers or group of numbers which show absolutely no relationship to each other anywhere in the sequence. At any point, all integers have an equal chance of occurring, and they occur in an unpredictable fashion” [1]. Random number generator (RNG) is indispensable in many areas like gaming, gambling, simulation, industrial testing, lotteries, randomized algorithms [2] [3], and it has a crucial role in cryptography. Random numbers should be uniformly distributed and statically independent. The measure for randomness is called entropy, which quantifies the degree of uncertainty. Claude E. Shannon introduced entropy in 1948 in his paper "A Mathematical Theory of Communication." [4]. The mathematical definition of entropy for a variable X is:

Я(х) = - X, PU = х) lo₈₁ Р(Х = х)

where Р(Х = х) is the probability that the variable X takes on the value .

The true random number generator does not fulfil the need of the applications that required random numbers, due to the inability of true random number generators to produce random numbers at the desired rate, they do not satisfy the requirements of some applications. Thus, pseudo-random numbers generator comes in the picture but with the security pitfalls. The goal of proposed pseudo-random numbers generators in this paper is to increase the security and output rate while reducing complexity. To increase throughput a graphics processing unit (GPU) has been used which is a massively parallel computation platform with thousands of cores, and provide high peak performance with low cost and power usage. GPU architecture is throughput oriented, which is miraculous for executing same instruction across various data (Single Instruction Multiple Data, oriented SIMD). NVIDIA introduced CUDA (Compute Unified Device Architecture) which is a parallel computing platform and API to utilize high-performance graphic processors for general purpose computations. CUDA program is divided into two parts: the host-side which is run on CPU and the device-side which is executed on the GPU [5]. This paper presents how the proposed generator is immune to the major vulnerabilities of PRNGs, and the speed of the generator is heightened with the help of graphics processing unit (GPU) as it provides the large number of FLOPs at low cost, and we show the performance of proposed generator on different three different systems.

• II.    Background

• A.    General Security Requirements of RNGs are [6]

Requirement 1: The output of random number generator should not have any statistical weaknesses.

Requirement 2: Even if the sub-sequences of random numbers are known it should be infeasible to compute or guess predecessors or successors with a probability higher than without knowledge of these sub-sequences.

Requirement 3: Even if the internal state is known it should be infeasible to compute or guess previous random numbers with a probability higher than without knowledge of the internal state.

Requirement 4: Even if the internal state is known it should be infeasible to compute or guess previous random numbers with a probability higher than without knowledge of the internal state.

• B.    Types of Random Number Generators

True random numbers generators (TRNGs): TRNG extracts the randomness from a natural phenomenon that has some entropy source. TRNGs are Stronger than PRNGs because the PRNGs are based on mathematics, and the mathematical proof of randomness is impossible, while TRNGs do not rely solely on mathematics but also on sets of physical postulates which lie outside of mathematics and serve as a non-deterministic source for producing random numbers. TRNGs are mainly used by online gambling companies, state security agencies and the product labelling and testing industry. Examples of TRNGs are radioactive decay, keystroke timing, atmosphere noise.

Limitations of TRNG:

• •    High price, due to expensive hardware

• •    complex design.

• •    Output not always available, the application speed will be bound by TRNG’s event’s speed.

• •    Less entropy is expected from the physical events.

Entropy source

Binary Conversion

Random bits sequence

Fig.1. True Random Number Generator.

Pseudorandom number generator (PRNG): It is a deterministic algorithm which generates a sequence of numbers (or bits) whose statistical properties are similar to the properties of the sequence of truly random numbers. A PRNG has an internal state which is also known as a secret state which produces deterministic output that is indistinguishable from random numbers to those who do not know and cannot guess the internal state. A PRNG starts from an arbitrary initial state which is defined by seed, the internal state updates on each request. The overall security of PRNG depends on its seeds and the algorithm, so the seed should be secret and random.

A PRNG is considered as a single point of failure for the majority of cryptosystems, and it differs from true random number generator as the pseudorandom number generator is necessarily periodic and has been derived from a deterministic algorithm. The period after which PRNGs repeat the same sequence of bits is called depth of PRNG, and it is very dangerous, as the repeated sequence makes the system free lunch for adversaries.

TRNGs are more secure than PRNGs as the degree of randomness is higher, but PRNGs are essential as they can quickly generate a large sequence of random numbers using small a seed and they are also cost effective.

Seed

DeterministicAlgorithm

Pseudo random bits sequence

Fig.2. Pseudo Random Number Generator.

Characteristics of Pseudo-Random Number Generator:

• •    Deterministic algorithms are used to generate random numbers.

• •    Randomness: The sequence should appear random even though it is deterministic.

• •    Reproducibility: The generator produces the same sequence when the seed is repeated.

• •    Period length: It is the length of the cycle after which the generator starts to produce the same sequence, and the reseeding is required.

• •    Seed: The security of pseudorandom number generators are based on the seed, if the seed is known to others then the sequence will be predictable.

• •    Unpredictability: Pseudo-random numbers should exhibit unpredictability.

• •    Forward unpredictability: If the seed is secret the next sequence should be un-guessable even the previous sequences are known.

• •    Backward unpredictability: generator should be irreversible; the intruder should not be able to guess the seed by knowing generated sequences.

• C.    Linear Feedback Register (LFSR)

Linear Feedback Register is a set of cyclic binary states, and the current state is the result of computation of its predecessor state. The initial value of the LFSR is known as a seed, and each iteration creates a different state of ‘n’ bits. The inner state is shifted to the right; the rightmost bit is the output. The bit positions affecting the next state are known as taps. The taps are XORed successively with the output bit and replace the leftmost bit; this operation is known as Linear feedback.

An LFSR with well-chosen taps can produce a sequence of bits that appears random and has a very long cycle which is called m-sequence (maximum sequence).

N-bit LFSR has a period length of 2n-1[7]. A 32bit LFSR can produce over 4 billion random bits sequence. The LFSR sequence depends on the seed value, the tap positions, and the feedback type.

The necessary conditions for maximal-length LFSR are:

• •    The number of taps should be even.

• •    The feedback vector must be relatively prime; there must be no divisor other than one common to all taps.

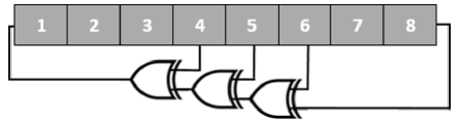
Fig.3. 8-bit LFSR with Feedback Polynomial x8 + x6 + x5 + x4 +1 with Maximum Length of 255.

• III.    Related Work

There are incalculable works concerned with the generation of uniformly distributed random number sequence in the last decade. There are simple arithmetic algorithms like a linear congruential generator, lagged Fibonacci generator, linear feedback shift register generator [8], but many of these early PRNGs have inadequacies [9] [10]. There are many proposed pseudorandom numbers generators; some are stream cipher based [11] [12] [13], some are temporal [14], and some are chaotic based [15] [16], and some are cellular automata-based [17] [18], but the problem is there is a trade-off between security, complexity, and the output rate.

Kelsey, J., Schneier [19] have discussed some vulnerabilities that most of the exciting PRNGs enduring of it; they also discussed the countermeasures of these vulnerabilities. A potent immunizer for PRNGs is a hash [20], and it was considered as an impediment solution, but with the help of parallelism nature of GPUs, it becomes a favorable solution. Many studies proved the enhancement of hashing speed using GPU [21] [22].

• IV.    Problem Statement

PRNGs are indispensable for cryptography applications, wherever necessary the output shall be unpredictable from previous outputs. There are many limitations with PRNGs.

• A.    Limitations of PRNGs

Short period of PRNG (or depth of PRNG): The period of PRNG is a major problem as the PRNGs will repeat their sequences after they reach the end of seed’s period, the repeated sequence makes the output of PRNGs predictable. One of the ways to extend the period of a PRNG is to use LFSR as it has a period length of 2n-1 if the chosen feedback vector is designed according to the above rules and another way is by increasing the reseeding rate which is not a good option. The period of PRNG should be long enough to support practical applications.

Bias in PRNGs: It means a certain number occurs more often than others, and it has been proved by Paul Peach [23] that any PRNG based on mathematical formula will contain patterns and periodicities that act as constraints upon their variability. We used LFSRs because they have little bias and as the size of LFSR is increased the bias becomes negligible.

Predictability: The mathematician Berlekamp-Massey found that a given N-bit LFSR with unknown feedback polynomial requires only 2N bits to predict the 2N+1th bit. The best way to impede the disclosure of internal structure of LFSR is to use cryptographic hash function so that we can securely generate a long sequence of bits (m-sequence) without the need of re-seeding the PRNG before generation 2ⁿ-1 bits.

Seed should be secret: The use of seed is to initialize the initial state of PRNG, and the seed completely determines the PRNG-generated sequence. If the seed value is known then the entire PRNG is compromised, so the initial PRNG security phase is to secure the seed, for that we used a pool of seeds to increase the complexity of guessing the selected seed due to permutation and combination. Also, we have used a secret key, so the output is not dependent only on the seed value.

Speed: Speed is the main problem of TRNG and the Hybrid random number generators (PRNG + TRNG = HRNG). Since most of the time, the seed sources produce entropy at a low rate.

• B.    Attacks on PRNGs [19]

Robustness against attacks is the distinction between general PRNG that used in stochastic simulations and the cryptographically secure PRNG.

The purpose of attacks on PRNGs is:

• •    Predict the unknown output of PRNG.

• •    Gain information about the inner state and thus, know the future output.

• •    Manipulate the output of the PRNG.

The possible attacks on PRNGs are categorized into three categories: cryptanalytic attacks, input based attacks, and state compromise extension attacks.

Direct cryptanalytic attack: In this kind of attack, the attacker tries to get the information about the inner state or predict the future output of PRNG by having knowledge of previous output. This type of attack can be prevented by using cryptographic primitives like hash functions.

Input-Based attacks: In this attack, the attacker gets the control of PRNG inputs and able to modify the input to the PRNG which allows an attacker to make inferences about the internal state of the PRNG. It may be further categorized into known input, replayed input, and chosen input attacks. The goal of this kind of attack is to minimize the possible outputs of PRNG, so the attacker can drive the output or force the PRNG to produce designated output.

• •    Chosen input attack: In this type of attack the attacker can directly manipulate the input of the PRNG, to force the generator to cycle or repeat a specific previous output.

• •    Replayed input attack: It is similar to chosen attack, but the attacker replays the existing input without modifying it.

• •    Known input attack: In this attack, the attacker uses the knowledge of the input to limit the possible outputs of PRNG. This attack is possible if the entropy of input is low or the input is observable (e.g., using latency of network hard drive as a seed).

State Compromise Extension Attacks: In this attack, the attacker uses the knowledge of compromised state to derive the previous or future output. The state can be compromised if there is a security breach in a system on which the generator is running, or the generator was seeded from a source which was accessible by an attacker or due to insufficient entropy.

• •    Backtracking Attack: The attacker uses the knowledge of compromised state to derives previous outputs.

• •    Permanent Compromise Attack: Using the knowledge of compromised state, the attacker can derive both the previous and the future output. The generators cannot be recovered from a compromised state until they are re-seeded.

• •    Iterative Guessing Attack: The attacker uses the knowledge of internal state at time t and observes the subsequent outputs to learn the internal state at time t+ε. This attack utilizes guessable unknown input (seed) to determine the internal state at time t+ε.

• •    Meet-In-The-Middle Attack: It is a combination of Backtracking Attack and Iterative Guessing Attack. The knowledge of internal state at time t and t+2ε is used to determine the state at time t+ε.

• •    Correlation-Attack : It is the most common attack on LFSR based PRNG; it exploits a statistical weakness of PRNG. The hash function can resist the correlation attacks, but to add one more security level we have used the mod, so it will be incredibly intricate to find out what was the original output of PRNG. And it is essential to prevent this type of attacks because it becomes harder to recover if the attacker at any time is able to acquire the internal state.

• V.    Proposed PRNG

We have proposed a cryptographically secure PRNG which is fast and immune to many known cryptanalysis attacks on PRNGs. This PRNG consist of a sampling unit, the pool of samples, sample selector, 256-bit seed, 256- bit salt and a hash function. The sampling unit takes the sound as an input from a sound file or via microphone and generates 16-bit samples which then be stored in the pool of samples which can hold up to 1024 samples.

As suggested by Bruce Schneier [19], the best Armor for PRNG is the pool which cumulates the incoming events that contain entropy, and collect them till you have sufficient events to seed the internal state without the attacker having the capability to guess the content of pool. The sampling function continuously runs in the background and overwrite the content of pool.

The pool contains 1024 unique samples so to guess the pooled samples there are 2 ^1024 combinations and then for each combination there are LD!4^z possibilities to guess the seed, so this complexity helps to immunize the

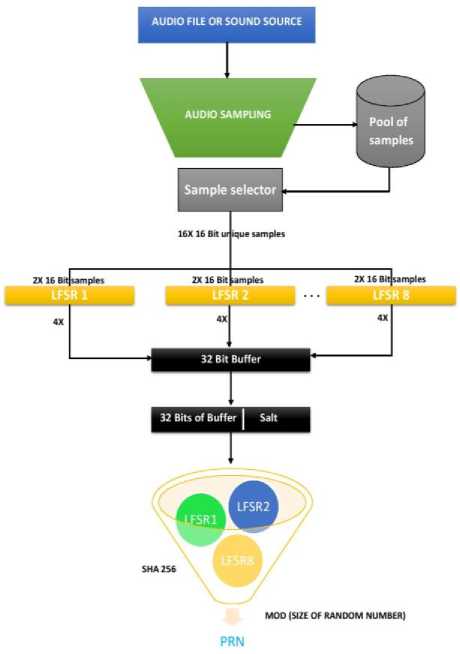
Fig.4. Architecture of Proposed PRNG.

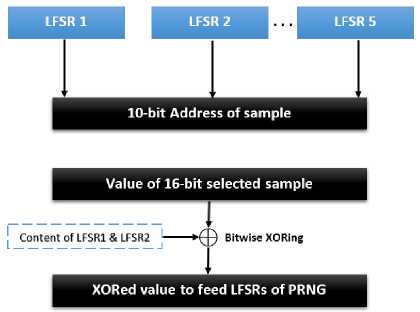
Fig.5. Architecture of selector.

PRNG by making it impossible to guess the internal state in forward manner. The sample selector randomly selects 32 samples from the pool out of which 16 samples are used as a seed and the other 16 samples are used as a salt. The seed then load into eight 32-bit LFSRs, two samples per LFSR and the taps of LFSRs should be carefully chosen to produce an m-sequence (maximum depth). Each of eight 32-bit LFSRs are shifted once in a single iteration, and there are four iterations to produce 32 bits which then will be stored in a 32-bit buffer. The content of the buffer will then combine with the 256-bit salt (it is preferred that size of salt must be equal to the size of the output of hash function) and be passed to the hash function (SHA-256) which will mask the inner state of the generator. The mod operation can be applied to the output of the hash function to limit the range and to make the statistical deviation much harder to detect by limiting the number of bits of random data in a single request.

Hashing salt with the content of buffer prevent the dictionary and rainbow attacks, thus prevent revealing the information of internal state in a reverse manner, and it is critical because any leakage of internal state content will compromise the entire PRNG. Reseeding of the generator and changing the salt required after generating one billion random numbers.

The selector is composed of five 8-bits LFSRs which are fed with 40 bits of 12-digit password and shifted twice to generate 10-bit sample address to select a random sample (address space of pool is 210) see Figure 5. All selected samples are XORed with the content of first and second LFSRs of the selector before feeding them into LFSRs of PRNG, XORing will filter out the effect of injected data. Samples with all ones or all zeroes are not accepted, and all the containing samples should be distinct.

The collection of entropy should be performed locally, as the network sniffing can reveal seed information. This PRNG is immune to Direct Cryptanalysis Attack, Input Based Attack, State Compromise Extension Attack, Correlation Attack, Brute-force attack. Table 1 showing the PRNG threats and the corresponding methods to immune the PRNG to those threats.

• VI.    Algorithm

The algorithm is divided into three threads execute in parallel to achieve higher performance, where the sampling thread is continuously run in the background.

Initialization:

• 1:    Get Password // 12 digit password

Thread 1: Sampling

• 2:    Source ← audio file or microphone interface

• 3:    while not exit do

• 4:    Pool [n] ← Sample(Source) //samples with all 1 or 0 should be filter out

• 5:    IF n = Pool_Top - 1

• 6:    Then n ← 0

• 7:    Else n ← n + 1

• 8:    End while

Thread 2: Selector

• 9:    LFSRs [5] [8] ← Binary( Password )

  // fill LFSRs with 40 bit binary of password

• 10:    For i ← 1 to 32 do

• 11:  Address ← Shift( LFSRs , 2)

  //shift all the LFSRs twice

• 12:    Sample ← Select( Address )

  // select sample from a given address of pool

• 13:    Seed ← Sample ⊕ LFSRs [1,2]

  // XOR sample with the content of LFSR 1 & 2

• 14:    End For

• 15:    For i ← 1 to 32 do

• 16:  Address ← Shift( LFSRs , 2)

• 17:    Sample ← Select( Address )

• 18:  Salt ← Sample ⊕ LFSRs [1,2]

• 19:    End For

• 20:    PRNG( )

Table 1. Threats and the Corresponding Protection

Threat	Protection
Direct cryptanalytic attack	Hash
Input-Based attacks	XOR, Random sample selector, Pool of samples
- Chosen input attack	XOR, Random sample selector
- Replayed input attack	XOR, Random sample selector
- Known input attack	Pool of samples
State Compromise Extension Attacks	Salt, Hash
- Backtracking Attack	Hash, and LFSR also don’t allow this without completing the cycle.
Correlation attack	Hash, Mode

Thread 3: PRNG

• 21:    LFSRs [8] [16] ← Seed

• 22:    Buffer ← Shift( LFSRs , 4)

  //shift all LFSRs 4 times

• 23:    RN ← SHA-256( Buffer + Salt )

  //Output random number (sequence of bits)

• 24:    n ← n + 1

• 25:    IF n > one billion

• 26:    Then Selector( )

• 27:       n ← 0

• 28:    End IF

• VII.    Test Results

The NIST statistical test suite is used to check whether the given sequence of bits is random or not, this suite tests the null hypothesis (H0), which verify that the input sequence of bits is random. This test suite consists of 15 tests which are probabilistic, and there are two types of errors, type I error is occurred when the data are random and H0 is rejected, and type II error is occurred when the data are nonrandom and H0 is accepted. ∝ denotes the probability of a type I error, and it is known as the level of significance of the test. Statistical tests results represent by p-value which is a real value between 0 and 1, and H0 is accepted only if p-value >∝, which is in this case 0.01.

Table 2. Test Results

Test	Min. P value	Max. P value	Ratio of success tests
Frequency	0.212	0.780	100%
Block-frequency	0.109	0.467	100%
Cumulative-sums (forward)	0.533	0.878	100%
Cumulative-sums (reverse)	0.224	0.696	100%
Runs	0.878	0.957	100%
Longest-runs of ones	0.689	0.707	100%
Rank	0.381	0.636	100%
FFT	0.403	0.562	100%
Overlapping-templates	0.110	0.264	100%
Non-periodic-templates	0.090	0.466	100%
Universal	0.248	0.844	100%
Approximate entropy	0.361	0.398	100%
Random-excursions	0.456	0.743	100%
Random-excursions Variant	0.584	0.821	100%
Serial 1	0.372	0.590	100%
Serial 2	0.022	0.414	100%
Linear-complexity	0.164	0.719	100%

NIST statistical test suite [24] has been used in this study to assess randomness of generated sequences by the presented generator. All the tests are performed ten times on different 256-bits outputs of the PRNG, Table 2 shows the results of maximum and minimum p-values of tests and the percentage of success out of 10 for each test. Figure 6 is a numerical analysis of test results which shows the difference between the maximum and the minimum p-value of each test.

To execute the benchmark, we used three different systems. SYSTEM 1: Intel i7-7920HQ quad-core CPU with clock speed 3.10 GHz and maximum Turbo Frequency 4.10 GHz, with 16-GB DDR4 main memory clocked at 2400 MHz, and an NVIDIA TITAN X Pascal graphic card which is based on GP102 graphics processor, and has 3,840 CUDA cores spread across 30 streaming multiprocessors (SM) and 6 graphics processing clusters (GPCs), along with 12288 MB GDDR5X memory, and 384-bit bus width. SYSTEM 2: Intel i5-7287U dual-core CPU with clocked speed 3.30 GHz and maximum Turbo Frequency 3.70 GHz, and 8 GB DDR4 main memory clocked at 2133 MHz. SYSTEM 3: Intel i3-4030U dualcore CPU with clock speed 1.90 GHz, and 4 GB DDR3 main memory clocked at 1600 MHz.

SYSTEM 1 is used for GPU-based implementation of the algorithm, which results in extremely high throughput, and the SYSTEM 2 and SYSTEM 3 are used for standard CPU based implementation. Table 3 shows the quantity of generated random numbers with respect to time and the number of thread. SYSTEM 1 has the highest generation rate it can produce 12 million random numbers of 256 bits per second; the result clearly shows that use of a hash in generating pseudo-random numbers is not a bottleneck as we can achieve much higher generation rate using multiple graphics processing units.

Table 3. Speed Comparison on Different Systems

System name	Quantity of generated random numbers	Number of threads	Time in seconds	Speed in bits per seconds
SYSTEM 1	12000000	2490	1 sec	30.72 Gb/s
SYSTEM 2	3000000	3	30 sec	25.6 Mb/s
SYSTEM 3	3000000	3	45 sec	17.066 Mb/s

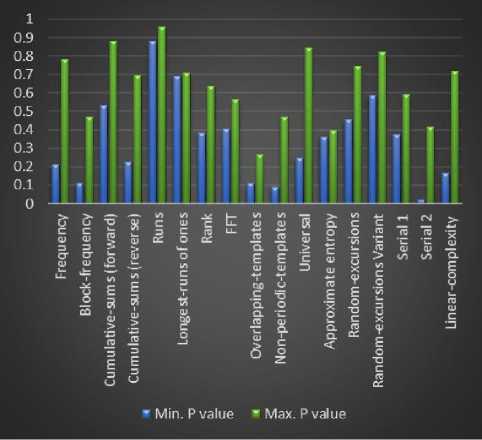
Fig.6. Numerical Analysis of Test Results.

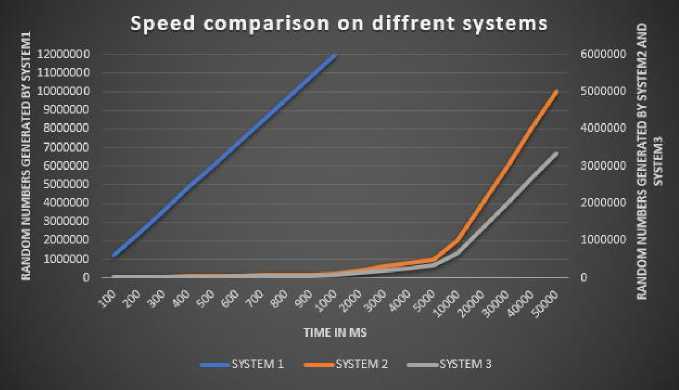
Fig.7. Speed Comparison on Different Systems

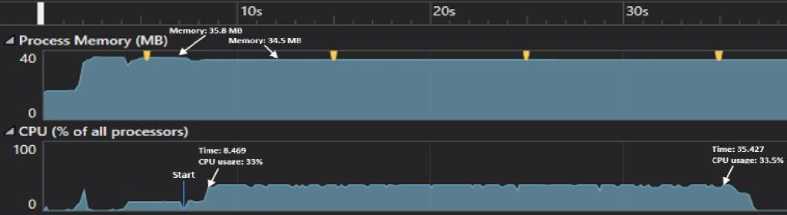
Fig.8. CPU and Memory Consumption of SYSTEM 2.

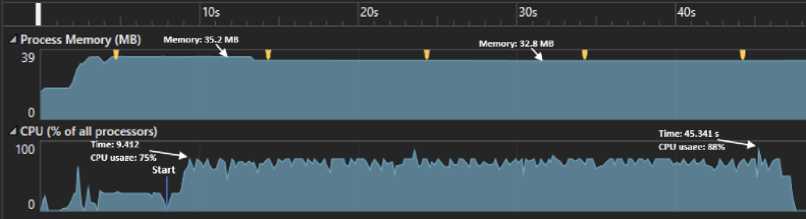
Fig.9. CPU and Memory Consumption of SYSTEM 3.

SYSTEM 1 is used for GPU-based implementation of the algorithm, which results in extremely high throughput, and the SYSTEM 2 and SYSTEM 3 are used for standard CPU based implementation. Figure 7 is a graph that compares the generator speed on different systems; the left axis represents the quantity of random numbers generated by SYSTEM 1 while the right axis represents the generation rate of SYSTEM 2 and SYSTEM 3. Figure 8 and Figure 9 show the CPU and memory consumption of SYSTEM 2 and SYSTEM 3 respectively for generating 3 million random numbers, in both the figures start point indicates the point at which generation of random numbers started before that point represent the usage of program load and sampling only.

• VIII.    Conclusion

In this paper, we propose a cryptographically secure pseudo-random number generator which has protection to major PRNG threats and required less memory and CPU capacity, and is easier in implementation. The proposed generator has been subjected to NIST SP 800-22 statistical test suite and remarkably passes all the tests. We also compared the performance of proposed generator on different systems and proved that using graphics processing unit can significantly increase the performance.

Acknowledgment

We would like to take this opportunity to express our profound gratitude and deep regard towards Prof. Moin Uddin, for his exemplary guidance, valuable feedback and constant encouragement throughout the duration of the paper. His valuable suggestions were of immense help and his perceptive criticism kept us working harder to give the desired result.