Адаптация бизнес-модели международных компаний в условиях санкционного давления

MACBETH – это один из алгоритмов многокритериального принятия решений. Он относится к классу многокритериальных методов принятия решений с качественными оценками (хотя может и использовать количественные показатели).

Рассмотрим работу этого метода на примере выбора хедлайнера для фестиваля. Сначала для этого метода надо определить критерии, их типы и веса, а также альтернативы (в нашем случае, это артисты).

На основе анализа ресурсов сети Интернет и пользовательских предпочтений были выделены следующие критерии:

• -    количество прослушиваний на стриминговых сервисах в месяц ( C l , максимизирующий тип, вес v l = 0.083);

• -    соответствие тематике фестиваля ( C m , максимизирующий тип вес v m = 0.167);

• -    гонорар артиста и дополнительные расходы ( C e минимизирующий тип, вес v e = 0.167);

• -    график гастролей и гибкость условий ( C f , максимизирующий тип, вес v f = 0.25);

• -    репутация артиста ( C r , максимизирующий тип, вес v r = 0.083);

• -    потенциал нарушения порядка фанатами (C d минимизирующий тип, вес v d = 0.25).

В качестве альтернатив были выбраны следующие исполнители:

• -     Mahath Gulf;

• -     Paul Rhodes;

• -      Trifecta;

• -     Clearly;

• -      Jessica Riff;

Charlotte Polka

На первом этапе требуется заполнить матрицу решений SM . В таблице 1 представлены исходные данные, отражающие значения альтернатив по каждому из выделенных критериев.

Таблица 1 – Изначальная матрица решений

Альтернативы	Прослу-шивани я	Соответствие тематике	Расходы ($/выст.)	Условия артиста	Репутация артиста	Потенциал нарушения порядка
Mahath Gulf	4382521	Сильное	99591	Довольно гибкие	Отличная	Слабый
Paul Rhodes	1872847	Довольно сильное	57837	Негибкие	Хорошая	Довольно сильный
Trifecta	407691	Довольно слабое	5609	Очень гибкие	Хорошая	Слабый
Clearly	18799049	Очень сильное	184742	Довольно гибкие	Идеальная	Очень слабый
Jessica Riff	450987	Среднее	3007	Очень гибкие	Идеальная	Средний
Charlotte Polka	2202083	Очень сильное	54947	Негибкие	Хорошая	Средний

Поскольку в методе Macbeth для подсчёта финальной оценки используются числовые значения, то приведенные качественные оценки альтернатив требуется преобразовать в числовые. Переводная шкала имеет следующие градации:

• -    очень сильно / идеально / очень гибко – 10;

• -    сильно / отлично / гибко – 8-9;

• -    довольно сильно / хорошо / довольно гибко – 6-7;

• -    средне – 5;

• -    довольно слабо / довольно плохо / довольно негибко – 3-4;

• -    слабо / плохо / негибко – 1-2;

• -    очень слабо / отвратительно / очень негибко – 0;

В таблице 2 представлена матрица решений, которая будет использоваться в дальнейших подсчётах.

Таблица 2 – Матрица решений с числовыми значениями

Альтернативы	Прослушивания	Соотве тствие тематике	Затраты ($/выст.)	Условия артиста	Репутация артиста	Потенциал нарушения порядка
Mahath Gulf	4382521	8	99591	7	8	3
Paul Rhodes	1872847	6	57837	2	6	6
Trifecta	407691	4	5609	10	7	2
Clearly	18799049	10	184742	6	10	1
Jessica Riff	450987	5	3007	10	10	4
Charlotte Polka	2202083	10	54947	2	7	4

Следующим шагом является определение максимального и минимального показателя для каждого критерия, с использованием соответственно формул 1 и 2:

b j = max ( X j ) ,j e[ 1 ,m ]                              (1)

w j = min ( x j ) ^,j € ^{[1 ,m ]}                               (2)

Для рассмотренного примера получаются следующие значения:

• -     b l = 18799049, w l = 407691;

• -     b m = 10, w m = 4;

• -     b e = 184742, w e = 3007;

• -     b f = 10, w f = 2;

• -     b r = 10, w r = 6;

• -     b d = 6, w d = 1.

Если тип критерия – минимизирующий, то для этого критерия значения b и w меняются местами. В противном случае они остаются без изменений. В решаемой задаче минимизирующими критериями являются «гонорар артиста и дополнительные расходы» (Сe) и «потенциал нарушения порядка фанатами» (Сd), поэтому для них значения b и w меняются:

• -     b e = 3007, w e = 184742;

• -     b d = 1, w d = 6.

Далее для каждого значения в матрице пересчитываются значения, с использованием формулы 3:

SM_i = SM j w-v i _e[1 ,n ] ,j _e[ 1 ,m ]                (3)

^,j    b - w j    j

Где SM – матрица решений, w – наихудшие значения критериев, b – наилучшие значения критериев, v – веса критериев, m – количество критериев, n – количество альтернатив.

В таблице 3 представлена матрица решений после применения формулы 3:

Таблица 3 – Матрица решений с числовыми значениями

Альтернативы	Прослушивания	Соотве тствие тематике	Затраты ($/выст.)	Условия артиста	Репутация артиста	Потенциал нарушения порядка
Mahath Gulf	0.018	0.111	0.078	0.156	0.042	0.15
Paul Rhodes	0.007	0.056	0.116	0	0	0
Trifecta	0	0	0.164	0.25	0.021	0.2
Clearly	0.083	0.167	0	0.125	0.083	0.25
Jessica Riff	0	0.028	0.167	0.25	0.083	0.1
Charlotte Polka	0.008	0.167	0.119	0	0.021	0.1

На последнем этапе значения в получившейся матрице складываются по формуле 4:

m

R i = S SM j ^[ 1 ,n ]                  (4)

j = 1

Где R – вектор результатов, SM – матрица решений, m – количество критериев, n – количество альтернатив.

Для решаемой задачи сумма результатов будет выглядеть следующим образом:

• -     R 1 = 0.555;

• -     R 2 = 0.179;

• -     R 3 = 0.635;

• -     R 4 = 0.708;

• -     R 5 = 0.628;

• -     R 6 = 0.415.

Самая лучшая альтернатива определяется как компонента вектора R имеющая наибольшее значение. В данном случае, 4-ая альтернатива, т.е. артист с именем Clearly, является наилучшей.

Также для решения задач методом MACBETH было разработано программное решение на языке Python с использованием библиотеки PySide6, являющейся реализацией фреймворка Qt.

Вначале в программе требуется ввести критерии и альтернативы. Также для критериев требуется указать вес и тип (за это отвечают галочки: если тип минимизирующий – значит требуется галочка). Стоит отметить, что строки снизу создаются автоматически, если в них что-то ввести; при этом, если строка будет пустая, то она будет удалена из матрицы. На рисунке 1 представлен ввод критериев и альтернатив.

ввод данных матрица результаты

с возвращением!

введите критерии введите альтернативы

Mahath Gulf

Paul Rhodes

Trifecta

Clearly

Jessica Riff

Charlotte Polka

аличество прослушиваний) ] * □ гствие тематике фестиваля 2 С □ >ар артиста и доп. расходы 2 С О Гибкость условий         3 С □

Репутация артиста        1  С U нциал нарушения порядка 3 С О 1 : □

Рисунок 1 – Ввод критериев и альтернатив

Далее, после перехода во вкладку «Матрица», открывается матрица решений, заполненная нулями. Её надо заполнить соответствующими числовыми значениями. На рисунке 2 представлена заполненная согласно примера матрица решений.

ввод данных	оценка альтернатив
		lecTBO прослуши!	льне тематике ф>	э артиста и доп. [	’ибкость условий 'епутация артист.
матрица	Mahath Gulf	4382521	8	99591	7               8
	Paul Rhodes	1872847	6	57837	2                6
результаты	Trifecta	407591	4	5509	10              7
	Clearly	18799049	10	184742	6                10
	Jessica Riff	450987	5	3007	10               10
	Charlotte Polka	2202083	10	54947	2                     7                     I

Рисунок 2 – Ввод матрицы решений

Чтобы посмотреть рекомендуемые альтернативы, надо перейти во вкладку «Результаты», представленную на рисунке 3. Здесь представлены круговая диаграмма и гистограмма с результатами. Как можно увидеть, здесь также рекомендуется артист Clearly, однако неплохими хэдлайнерами для поп-фестиваля также могут быть Trifecta и Jessica Riff.

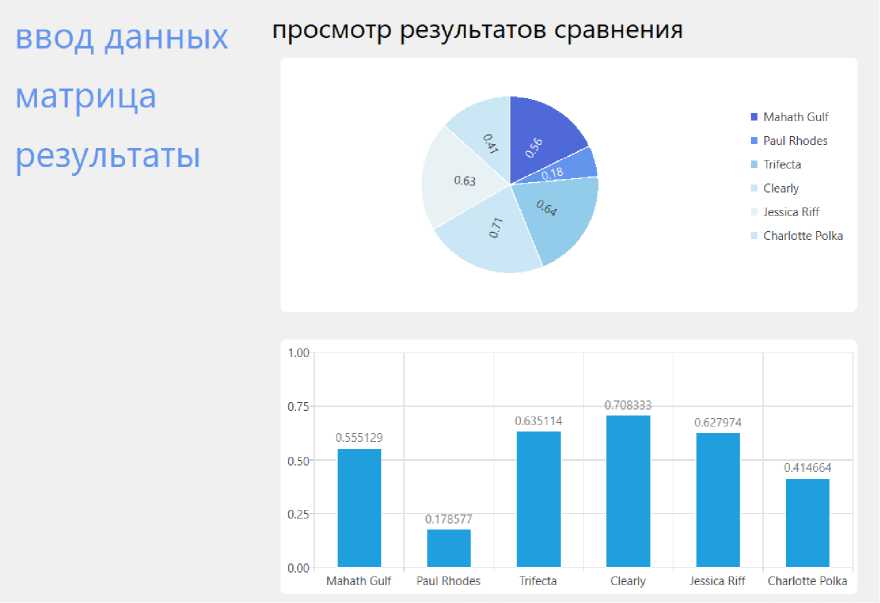
Рисунок 3 – Результаты сравнений

Программный код был выложен в открытый доступ на GitHub: