Адаптация дифференциального уравнения энергии к условиям топочных процессов в котельных агрегатах

Тенденции развития котельной техники ориентированы на повышение мощности, надежности и маневренности котельных агрегатов (КА) при переменном составе и теплотехнических характеристиках топлива. В этом плане значительная часть проблем прямо или косвенно связана с аэромеханикой и теплообменом в топке КА и соотношением механизмов переноса теплоты конвекцией и излучением. Можно полагать, что некоторые вопросы развития и усовершенствования котельной техники можно решить на основе анализа дифференциального уравнения энергии и адаптации его к условиям топочных процессов в топке КА.

Уравнение переноса энергии в топке КА

Уравнение энергии применительно к стационарному радиационно-конвективному теплообмену в потоке однокомпонентной вязкой и несжимаемой среды, поглощающей, излучающей и рассеивающей энергию излучения, имеет вид

Z div (qi ) = 0, (1) i где qi – векторы плотности теплового потока за счет теплопроводности, конвекции, внутренних источников теплоты и излучения соответственно, без учета перехода механической энергии в теплоту и диссипации энергии трения.

Рассмотрим плоское двумерное течение (wz = 0), где координата х направлена вдоль потока среды, а координата у – поперек течения, причем у = 0 на стенке КА; тогда уравнение энергии (1) примет вид р cp

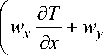
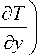
. (д2t д2t) (aq     aqu,у)

х —^+—т -I — +— 1+qv( дx2 ду2 J ( дx     ду )

Введем безразмерные переменные Х = х / l ₀, Y = y / l ₀, Re = w ₀ l ₀/ ν , W x = w x / w 0 , W y = w y / w 0 , θ = T / T 0 , <  q ) u , x q u,x /° о T о ⁴, <  q ) u , у = q uy М T з ⁴;

здесь l 0 – характерный размер рассматриваемой системы, м, который рационально принять равным продольному размеру топки КА, тогда все остальные размеры, как и текущие координаты точки, будут составлять доли от l 0 . В качестве характерной скорости w 0 , м/c, можно принять скорость в основном течении среды, вдали от пограничных слоев, остальные переменные с нижним индексом «0» характеризуются подобным же образом. При этом подразумевается, что уравнения сплошности, сохранения импульса и теплоотдачи на границах системы записываются как обычно. В этом уравнении также введена объемная плотность тепловыделения q_v , Вт/м³, которая принята постоянной, не зависящей от х и у , но это ограничение не принципиально, можно ввести в уравнение заданные пространственные или температурные функции объемной плотности тепловыделения, это не усложнит задачу анализа.

Подстановка этих величин в уравнение энергии (2) и несложные преобразования дают следующую зависимость

Wx — + W x 9X    y

9 Y

1 [ 929 929 +Pe .9X2 9 Y2

^d q >  u , y । Po ++ .

9 Y J Pe

1 ( ^ q ) u , x

Bo ( 9 X

Адаптация коэффициентов переноса к реальным условиям в топке

Для условий теплообмена в топке КА числа подобия, входящие в уравнение (3), имеют следующее теплофизическое содержание. Число Пекле Pe = Re · Pr характеризует относительный вклад в формирование температурного поля потока среды в топке КА конвективного механизма переноса теплоты по сравнению с теплопроводностью. Число Померанцева Ро = q_vl ₀²/λ T ₀ характеризует безразмерную плотность тепловыделений.

Число Больцмана Bo = (ρ w ) 0 c p /σ T 0 ³ описывает соотношение потоков энергии конвективного и радиационного характера, а величина 1 /Bo – участие радиационного механизма в формировании температурного поля потока среды в топке. Роль числа Во в радиационно-конвективном теплообмене аналогична роли числа Ре в кондуктивно-конвективном теплообмене: когда число Ре мало, можно пренебречь переносом тепла конвекцией по сравнению с переносом тепла теплопроводностью. Когда число Во имеет малую величину, можно пренебречь вкладом конвекции в формирование температурного поля потока среды по сравнению с излучением. Число Во легко преобразуется в комплекс чисел подобия Во = ( Re/N )( Pr/Bu ), где, кроме отмеченных Re и Pr , приведены числа N = σ 0 T ³ / λ k и Бугера Bu = kl 0 , где σ 0 = 5,67∙10^–8 Вт·м²/К⁴ – коэффициент излучения абсолютно черного тела, k – коэффициент ослабления топочной среды, м^–1. Число N является радиационно-кондуктивным параметром, число Bu характеризует излучательную способность топочной среды КА. Приведенная зависимость для Во является определением, получить из нее расчетные зависимости можно только после установления количественных зависимостей между величинами N , Re , Pr , Bu , Ро – аналитически, численно или экспериментально.

Выбор температур Т и Т 0 имеет принципиальное значение для анализа влияния числа Больцмана на процессы в топке КА и он связан с задачами анализа. Так, при определении результата теплообмена между координатами х 1 и х 2 можно записать уравнение для результирующего числа Больцмана ∆Во ≡ Во _рез.

Во рез =p WC p ( T_x - T 2 )/g ₀ ( T 14 - T 22 ) . (4)

При применении зональных методов расчета также может оказаться необходимым определение результата теплообмена в расчетной зоне по зависимости (4). При расчете интегральных характеристик теплообмена в некотором участке топки необходимо для всего участка определить число Во, основанное на средней по участку температуре, при этом температура для конвективного потока определяется как средняя арифметическая, Тср = (Т1 + Т2)/2, а для потоков излучения необходимо другое усреднение Тср4 = (Т14 + Т24)/2. Расхождение между средними температурами, подсчитываемыми по этим формулам, зависит от разности Т1 – Т2 = ΔТ: при ΔТ = 100 К разница 0,13 %, при ΔТ = 300 К разница достигает 1,2 %, что также можно признать допустимым.

С применением числа Во для оценки потенциала переносных свойств среды в топке КА также необходимо определить теплофизический уровень температур. В этом отношении можно принять за основу рекомендации ЭНИН [1], считая калориметрической температурой горения таковую без учета диссоциации продуктов сгорания Т кал и расчетную Т _расч, определяемую с учетом диссоциации. При полном сгорании топлива при стехиометрическом количестве воздуха без подогрева компонентов горения эти температуры соответствуют понятиям максимальной Т кал → Т макс и теоретической Т расч → Т теор . В принятом в стране методе расчета теплообмена в КА также применяется адиабатическая температура Т _а, которая была бы получена при сжигании реальной смеси топлива с воздухом без теплообмена с окружающим пространством. Но это, вероятно, больше относится не к термохимии процесса горения, а к условиям теплообмена горящей смеси с окружающими средами и ограждением. В научно-технической практике находят применение различные определения температуры горения в зависимости от задач анализа.

Число Во в виде сомножителя 1 /Во со знаком «минус» входит параметром во второе слагаемое правой части уравнения (3), это слагаемое описывает влияние потоков излучения на формирование температурного поля топки КА. Входящее в Во число Bu = kl 0 является параметром для суммы градиентов плотности потоков излучения { q ) _{u x} и { q ) _u y по координатным направлениям: Bu~ Egrad( { q ) _uxy ). С увеличением Bu снижается вклад конвективного механизма в пространственное температурное поле потока топочной среды. С другой стороны, посредством коэффициента ослабления k число Bu характеризует излучательную способность смеси газов с участием твердых частиц в топке КА.

Сравнив характерный размер топочного пространства l0, м, с величиной, обратной коэффициенту ослабления 1/k, получим Bu = l0/(1/k) = kl0; если Bu« 1,0, среда считается оптически тонкой, при Bu»1,0 среду считают оптически толстой (массивной). В топках КА при Bu = 2,8–3,6 оптическая массивность среды позволяет перейти в математическом описании вектора плотности потока излучения от интеграла интенсивности излучения по сферическому углу к градиентной форме описания qu, что и применено при выводе соотношений (2), (3). Приведенные выше соображения подтверждают достоверность примененной формы описания дифференциального уравнения энергии.

Преобразованное нелинейное уравнение (3) не поддается аналитическому решению, как и исходное (2), но позволяет выделить несколько аспектов анализа, связанных с теплофизикой и теплообменом. Левая часть уравнения (3) описывает изменение температуры потока безвихревого течения со скоростью, имеющей компоненты W x , W y в пространственном поле температур с градиентами ∂ θ /∂Х , ∂ θ /∂Y , и это изменение связано с действием конвективного, кондуктивного и радиационного механизмов, а также с тепловыделениями в потоке среды. Ограничение относительно безвихревого течения можно ослабить, если вместо молекулярного коэффициента теплопроводности λ м применить эффективный коэффициент, учитывающий турбулентные пульсации, λ_э ф = λ_м + λ_т.

Первое слагаемое правой части (3) в общем соответствует решению уравнения Лапласа, относящегося к теории потенциалов [2], которое в частном случае плоской поверхности дает описание плоских изотермических поверхностей, определяющая температура которых растет при удалении от поверхности экранов КА. Если раскрыть множитель перед скобкой 1/ Pe = λ эф /ρ wc p l 0 , то становится ясно, что первое слагаемое (3) описывает соотношение лапласовских температурных полей, образованных механизмами теплопроводности и конвекции.

В механизме переноса тепла конвекцией определяющим является число Рейнольдса, которое также формирует режим движения топочной среды – потока горящих газов и продуктов сгорания. При адаптации соотношений аэромеханики к условиям топок КА необходимо ориентироваться на соотношения и зависимости для нестесненного движения, так как развитие пограничных слоев от противоположных стенок топки не сказывается на формировании и развитии пограничных слоев в рассматриваемом сечении. Для оценки режима движения в этих условиях применяется локальное число Rex, связанное с числом Re, входящим в уравнение (3) зависимостью Rex = wρx/μ = Re·Lт = = (wρl0/μ)(x/l0), причем при рассмотрении продольного течения координата, направленная вдоль пото- ка, отсчитывается от начала течения х = 0, то есть от оси горелочных устройств до оси горизонтального газохода х = l0 , при этом безразмерная координата точки изменяется в пределах 0 ≤ Lт ≤ 1,0.

Количественные оценки коэффициентов переноса

Режим движения потока среды вдоль вертикальных стен топки КА определяется двумя критическими значениями Re x ,1 и Re x ,2 , первое соответствует турбулизации ламинарного пограничного слоя, второе – полностью развитому турбулентному пограничному слою. В научной литературе [3] обычно приводятся зависимости числа Рейнольдса от степени турбулентного возмущения потока для идеализированных условий в точке встречи потока с поверхностью х = 0. При этом учитывается влияние шероховатости стенки, условия формирования слоя при х = 0, угол встречи потока с поверхностью и другие факторы. В теплоэнергетических приложениях можно считать, что полностью развитая турбулентность наступает при Re x ,кр = 5·10⁵, откуда можно получить зависимость для х _кр = 5·10⁵μ _t /(ρ w ), результаты расчетов по которой приведены в таблице.

Определение х _кр имеет значение для адаптации процесса развития турбулентности и в этом отношении для расчета толщины турбулентного пограничного слоя δ можно использовать рекомендуемую в [3] зависимость δ = 0,37 x · Re x ^–0,2, которую для повышения точности графического изображения можно представить как δ усл ≡ δ/ x ^0,8 = = 0,37(μ t / ρ w) ^0,2. На основе приведенных данных можно сделать вывод о том, что при x ≥ x кр толщина турбулентного пограничного слоя растет и к точке х = 10 м составляет 0,189 м, а к точке х = 20 м достигает 0,329 м.

Потеря аэромеханической устойчивости на этом участке сопровождается появлением возмущающего пульсационного движения, которое накладывается на стационарный поток жидкости. Турбулентное движение в пограничном слое и в основном потоке в первом приближении можно представить в виде множества вихрей различных масштабов. Масштаб наибольших вихрей имеет порядок толщины пограничного слоя δ. Эти вихри пульсационного движения, как и другие, обмениваются энергией с усредненным движением, а за-

Зависимость координаты полной турбулизации пограничного слоя х _кр , м, (числитель) и условной толщины турбулентного пограничного слоя, δ_усл , м^0,2, (знаменатель) от плотности потока массы топочной среды, ρ w , кг/м²·с, и ее температуры Т , К

ρ w , кг/м2·с	Температура Т, К
	1473	1573	1673	1773
15	1,75/0,0300	1,82/0,0302	1,89/0,0305	1,96/0,0307
20	1,32/0,0284	1,37/0,0286	1,42/0,0288	1,47/0,0298
25	1,05/0,0272	1,09/0,0274	1,14/0,0276	1,17/0,0278
30	0,87/0,0262	0,91/0,0264	0,95/0,0266	0,98/0,0268

тем передают ее вихрям меньшего масштаба, и далее передача энергии продолжается с уменьшением масштаба. В самых мелких вихрях энергия диссипирует, то есть превращается в теплоту, вклад этого источника энергии незначителен по сравнению с другими источниками в уравнениях (2) и (3). Считается, что таким образом происходит диссипация кинетической энергии потока газов в топке КА вследствие работы сил вязкости; этот каскадный процесс передачи энергии является характерной чертой турбулентного движения. Другой его особенностью является трехмерность пульсационных движений, когда мгновенные значения скорости в произвольной точке турбулентного потока зависят от трех координат.

Третья особенность турбулентного пульсационного движения в замкнутом пространстве топки КА связана с взаимодействием возмущений давления с различными элементами объема топки. С увеличением размера вихрей при увеличении δ снижается частота пульсаций и увеличивается их амплитуда. Часть пульсационных колебаний в виде упругих волн распространяется вверх и вниз по потоку и может создать резонансные явления в элементах и конструкциях КА. Чем ниже частотный спектр колебаний, то есть чем больше δ, тем больше вероятность появления резонансных явлений, которые вносят помехи в процессы смешения и воспламенения топливно-воздушных сред, и вынуждают снижать тепловую нагрузку. Такие явления наблюдались в топках трубчатых печей нефтехимии и в камерах сгорания высокотемпературных металлургических воздухонагревателей. Кроме того, зоны локальной рециркуляции топочной среды, генерируемые крупномасштабной турбулентностью, создают благоприятные условия для улучшения качества сжигания топлива, но создают дополнительное сопротивление движению потока среды.

Режимные оценки, приведенные выше и в таблице, имеют предельный (mini-max) характер. Фактически, в условиях высокой турбулентности набегающего потока при х ≤ х _кр образование ламинарного пограничного слоя маловероятно, поэтому оценки турбулентности в пограничном слое имеют значение минимальных. С другой стороны, плотность потока массы ρ w = 10…20 кг/м²∙с для показателей среднего течения среды в топке КА недостижимы и могут наблюдаться только в применении к локальным показателям как максимальные.

Формирование потока топочной среды начинается от уровня горелок КА, при этом существенное влияние оказывают условия смешения и воспламенения смеси как от рециркулирующих потоков, так и излучением от горящих объемов и высокотемпературных зон топочного объема. Применение закона сохранения массы в виде уравнения сплошности для описания движения топочной среды дает определенные преимущества при выводе основных характеристик движения. Действительно, уравнение сплошности div(ρw) = 0 позволяет не вводить температурные поправки в характеристики течения, так как ρt = ρ0T0/T, wt = w0T/T0 , то (ρw)t = (ρw)0. Влияние температуры на характеристики потока среды проявляется через температурную зависимость абсолютной вязкости, которая в исследованном диапазоне Т = 1273…1773 К может быть представлена в виде μt = [47,9 + 0,022(T – 1273)]·10–6, кг/м·с = Н·с/м2 = = Па·с, для продуктов сгорания среднего состава (р = 0,101 МПа, СО2 = 13 %, Н2О = 11 %, N2 = 76 %).

Объемная плотность тепловыделений в потоке топочной среды q v , Вт/м³, в уравнении (2) принята постоянной, это допустимо в качестве первого приближения при анализе и адаптации процессов в топке КА. После преобразований уравнения (2) в уравнение (3) этот член преобразуется в отношение Ро/Pe ; интегральная оценка этого источника теплоты может быть получена делением тепловой нагрузки КА В р Q н ^р, Вт, на общий объем топки V T , м³: q v = B p Q н ^р /V T , где В р – расчетный расход топлива, кг/с. Но эта оценка не очень точно отражает функцию тепловыделения, так как сгорание топлива в объеме топки происходит неравномерно, для уточнения этого показателя рекомендуется применить те же соображения, что и для числа Во .

Заключение

Предложенная форма дифференциального уравнения энергии адаптирована к условиям процессов аэромеханики и теплообмена в топках КА, что позволяет производить количественные оценки в уравнениях переноса энергии в топках КА.

Сформулирован кортеж определяющих чисел подобия (критериев), являющихся параметрами в уравнении энергии.

Определены количественные значения чисел подобия и их степень влияния на теплофизические характеристики топочной среды, режимы течения и теплообмена.