Адаптация линейно-квадратичной модели для планирования режимов облучения в дистанционной нейтронной терапии

Планирование режимов облучения является важнейшим этапом в лучевой терапии злокачественных новообразований. В последние десятилетия основным руководством для такого планирования служит модель время – доза – фракционирование (ВДФ). Она применяется для планирования как гамма-, так и нейтронной терапии [2, 3], обеспечивая в течение длительного периода времени адекватный контроль за лучевыми реакциями [7, 8]. Модель ВДФ еще не утратила своей значимости, однако в последнее время в гамма-терапии ей на смену приходит линейно-квадратичная модель (ЛКМ) [10]. Понятен интерес к использованию последней и в нейтронной терапии. Известны работы, в которых предпринята попытка адаптировать ЛКМ к задачам терапии плотноионизирующим излучением [13, 14]. Однако эти работы в основном посвящены обсуждению результатов, полученных в экспериментальных исследованиях на клеточных структурах. Кроме того, известно, что относительная биологическая эффективность (ОБЭ) нейтронов сильно зависит от их энергии. Поэтому результаты таких работ невозможно перевести в практическую плоскость для решения задач дозиметрического и радиобиологического планирования нейтронной терапии, проводимой на источнике нейтронов с конкретными энергетическими характеристиками.

Цель исследования состояла в создании модификации ЛКМ, способной обеспечить планирование режимов облучения в дистанционной терапии злокачественных опухолей быстрыми нейтронами со сплошным энергетическим спектром и средней энергией ~6,3 МэВ.

Материал и методы

Нейтроны со сплошным энергетическим спектром при средней энергии 6,3 МэВ получены на циклотроне У-120 в реакции дейтронов на бериллии:

{d^Be^B^n ^.

Известно, что, согласно ЛКМ, выживаемость клеток может быть описана следующим математическим выражением:

5 = 5₀ехр[-(с^ + Д/²)], (1) где S_o и S – начальное число клеток и число клеток, выживших после облучения дозой d , соответственно; α и β – параметры модели, причем параметр α определяет долю летальных повреждений в клетках и выражается в Гр^-1, а параметр β определяет долю накапливаемых сублетальных повреждений и имеет размерность Гр^-2.

Из (1) видно, что выживаемость клеток по ЛКМ определяется произведением двух экспонент. Полагают, что функция ехр (- α d) описывает гибель клеток, обусловленную одномоментными двойными разрывами ДНК, а часть уравнения ехр (- β d ² ) – гибель клеток при накоплении одиночных разрывов ДНК.

Для того чтобы в дальнейшем иметь возможность более подробно проанализировать методические основы планирования нейтронной терапии на основе ЛКМ, поставлена задача найти параметры α и β в отдельности как для редко ионизирующего излучения, так и для нейтронов. В первую очередь знание параметров α и β в отдельности для обоих видов излучения, как показано нами ранее [4], необходимо для расчета важнейшей характеристики нейтронной терапии – зависимости ОБЭ нейтронов от дозы.

Для решения задачи, наряду с ЛКМ, применена многомишенная модель (ММ) клеточной выживаемости следующего вида:

S = SJM1-^^ (2)

В формуле (2) D_o и n – радиобиологические параметры, характеризующие степень радиочувствительности клеток.

Соотношение (2) широко используют в радиобиологии для оценки выживаемости клеточных структур при радиационном воздействии [11], а закономерности, получаемые на основе этой модели, дают удовлетворительное совпадение с клиническими результатами [3]. То есть функции (1) и (2) адекватно отражают реакцию облучаемой ткани на лучевое воздействие. Отсюда следует, что расчеты по этим двум моделям должны удовлетворительно совпадать друг с другом. Очевидно, что функции не могут совпадать во всей области своего определения, поскольку в полулогарифмических координатах функция (1) характеризуется непрерывно изменяющимся наклоном, а функция (2) имеет линейный участок. Однако можно потребовать, чтобы результаты расчета по обеим моделям были близки в области доз, используемых для лучевой терапии. На этом основании можно записать равенство:

exvY4^yd_y^ Р_уа²Д = Wl-exp(--^)p (3)

Значения рекомендуемых разовых очаговых доз (РОД) в терапии редко ионизирующим излучением лежат в пределах от 2 Гр до 10 Гр. Поэтому расчет проведен именно в этом интервале доз. Как и в модели ВДФ, в ЛКМ в качестве критических тканей взята кожа и так называемая нормальная соединительная ткань [2], для которых, согласно [3, 4], принято: Do = 1.66 Гр и n = 3.

Для нахождения параметров αγ и βγ, с наибольшей точностью обеспечивающих выполнение равенства (3) в заданном интервале доз, применен широко известный метод наименьших квадратов [1]. Уравнения, записанные в соответствии с методом наименьших квадратов и включающие параметры αγ и βγ, приведены в работе [6]. Кроме того, в расчетах учтено, что, согласно [10], для нормальных тканей по критерию ранних лучевых реакций значение α/β = 10 Гр.

Результаты и обсуждение

Изложенным способом определены наивероятнейшие значения параметров, а именно: αγ = 0,25 Гр-1 и βγ = 0,025 Гр-2. Результат отражен на рис. 1, из которого следует, что функции (1) и (2) хорошо совпадают в области РОД до 10 Гр, рекомендованных для лучевой терапии редко ионизирующим излучением.

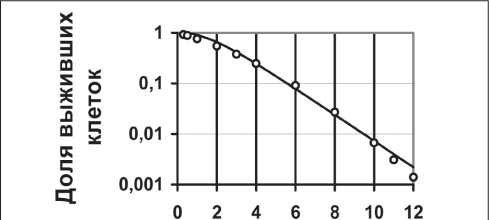
Доза гамма-излучения, Гр

Рис. 1. Сравнение функций (1) и (2) при α_γ = 0,25 Гр ^-1 и e_Y = 0,025 Гр ^-2 . Примечание:--ММ, ° ° ° - ЛКМ

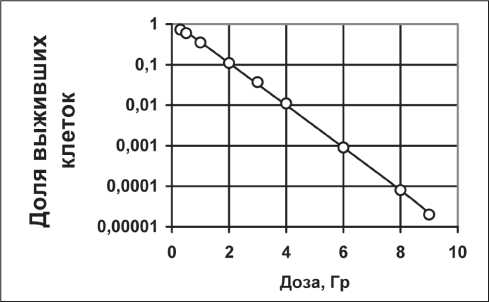
Рис. 2. Выживаемость клеток кожи по ММ и ЛКМ для нейтронов

При найденных значениях параметров αγ и βγ разработан специальный алгоритм определения параметров αн и βн, который подробно изложен в работе [4]. В результате получены следующие значения параметров линейно-квадратичной модели для терапевтического пучка нейтронов со средней энергией 6,3 МэВ: αн =1,03 Гр-1; βн = 0,023 Гр-2. На рис. 2 приведены зависимости выживаемости клеток кожи, рассчитанные по многомишенной (линия) и по линейно-квадратичной модели (точки) для нейтронов.

Видно, что результаты расчета хорошо совпадают, из чего можно заключить, что выбранный алгоритм расчета и полученные при этом численные значения параметров αγ и βγ, αн и βн верны. Основания для такого утверждения можно найти и в литературе. Так, в работе [13] параметры αн и βн в отдельности численно не определяются, но из нее следует, что βн ≈ βγ, а αн увеличивается ~ в 4 раза по отношению к αγ. Следовательно, полученные нами численные значения параметров αн и βн соответствуют имеющимся на сегодняшний день представлениям о соотношении параметров ЛКМ для гамма- и нейтронного излучения. Отмеченный рост параметра αн по отношению к параметру αγ означает, что для нейтронов увеличивается вклад одномоментных двойных разрывов ДНК по сравнению с гамма-излучением. То есть увеличивается доля клеток, гибнущих за счет одномоментных двойных разрывов, что, как известно [9], является характерной особенностью взаимодействия плот-ноионизирующего излучения, к которому относятся и нейтроны, с облучаемой средой.

Решение задачи по определению параметров αн и βн позволяет рассмотреть возможность применения

ЛКМ для планирования режимов нейтронной терапии. Модель ВДФ применяется давно, проверена и дает хорошие результаты [7, 8]. Поэтому для того, чтобы судить о возможности применения ЛКМ для планирования режимов облучения, необходимо сравнить результаты расчета по обеим моделям параметров курса терапии, определяющих частоту осложнений и степень выраженности лучевых реакций. Одной из таких характеристик является разовая очаговая доза. Получим математические выражения для ее расчета по модели ВДФ и по линейно-квадратичной модели.

Формула для фактора ВДФ в нейтронной терапии при равномерном режиме фракционирования имеет вид [5]

ВДФ = 6,9 х N х ^^1Д8 х JT⁰’¹³

где N – число сеансов терапии; d – однократная доза, Гр; X – временной интервал между сеансами терапии, сут.

Выражение (4) можно записать в виде

BДФ = 6,9xNxxxd^wxx-^uз.       (5)

Учитывая, что в (5) N × x = Т , можно получить формулу для расчета однократной дозы на основе модели ВДФ:

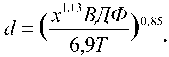
При расчете однократных доз для полных курсов терапии, характеризуемых значениями ВДФ = 100 и x = 1, формула (6) примет вид:

d = 9,7 × T ^-0,85.                                     (7)

Аналогом фактора ВДФ в ЛКМ служит понятие «суммарный биологический эффект», который определяют соотношением [10]:

СЭ = d × N (α/β + d ).                      (8)

Если рассматривать курсы лучевой терапии, полностью исчерпывающие толерантность нормальных тканей при ежедневном облучении, когда Т = N , то

СЭ = d × Т (α/β + d ).                       (9)

Из (9) для однократных доз, соответствующих полным курсам нейтронной терапии при ежедневном облучении, на основе ЛКМ можно получить выражение

, - off / В + l(off / В)² + 4Т х СЭ]⁰’⁵

от                *       (10)

Если учесть, что для быстрых нейтронов αн/βн= 45 [6], а пределу толерантности нормальных тканей соответствует значение СЭ = 720 [10], то выражение (10) может быть приведено к виду вающим толерантность нормальной ткани, считают режим с T = 28 сут; N = 12; d = 1,3 Гр [12]. Поэтому в расчетах по (4) и (11) максимальная длительность курсов принята равной Т = 28 сут.

На рис. 3 приведены рассчитанные по (4) и (11) зависимости однократной дозы от длительности курса в нейтронной терапии при ΔТ = 1 для режимов фракционирования, эквивалентных по своему воздействию на нормальную ткань; нижний график – расчет по модели ВДФ, верхний – расчет по ЛКМ. Видно, что во всем диапазоне Т зависимости удовлетворительно совпадают.

Представляет интерес сравнение степени расхождения расчетов РОД по модели ВДФ и ЛКМ для нейтронной терапии, в которой ранее ЛКМ не применялась, и для гамма-терапии, при которой уже есть опыт использования ЛКМ. Чтобы провести такое сравнение, получим формулы для РОД в гамма-терапии на основе модели ВДФ и ЛКМ. Выражение для фактора ВДФ в гамма-терапии имеет вид

^_-4577^+[(457У^28807^ IT

ВДФ = 1,2 × N × d ^1,538 × X ^-0,169,               (12)

Для расчета доз по (4) и (11) необходимо выбрать диапазон длительности курсов нейтронной терапии. Нейтронную терапию, по сравнению с гамма-терапией, проводят на более сложных и дорогих установках. В связи с этим исследователи стремятся к тому, чтобы курсы нейтронной терапии были короче традиционно принятых курсов гамма-терапии.

При средней энергии нейтронов 6,3 МэВ, которую обеспечивает применяемый в нашем случае циклотрон, базовым курсом, полностью исчерпы- откуда для ежедневного облучения при

ВДФ = 100

d = 17,7 × T ^-0,65.               (13)

Для РОД по ЛКМ в гамма-терапии можно получить формулу

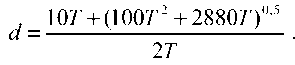
На рис. 4 приведены зависимости РОД в гамматерапии при ежедневном облучении, рассчитанные

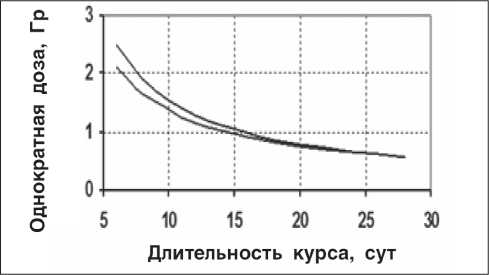
Рис. 3. Зависимости однократной дозы от длительности курса нейтронной терапии

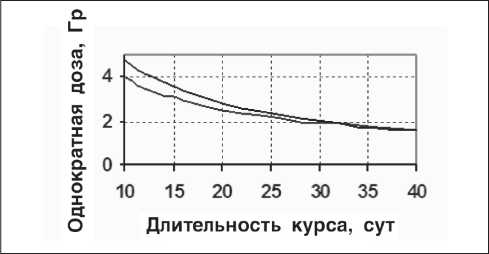
Рис. 4. Зависимости однократной дозы от длительности курса гамма-терапии

по (13) и (14). Так же, как и на рис. 3, нижняя линия – расчет по модели ВДФ, а верхняя – расчет по ЛКМ.

Сравнение графиков, изображенных на рис. 3 и рис. 4, показывает, что и в нейтронной, и в гамматерапии расхождение между значениями РОД для модели ВДФ и ЛКМ возрастает с уменьшением длительности курса. При этом относительное различие в значениях РОД для гамма-терапии, например, при Т = 10 сут составляет ~20 %, в то время как для нейтронной терапии ~12 %. То есть разработанная для нейтронной терапии модификация ЛКМ обеспечивает заметно меньшее расхождение результатов расчета по сравнению с моделью ВДФ, чем ЛКМ, уже применяемая в гамма-терапии. Из этого следует, что применение ЛКМ, разработанной для нейтронной терапии, способно обеспечить вполне адекватный контроль за лучевыми реакциями.

Привлечение ЛКМ для решения задач планирования нейтронной терапии позволит расширить способы и возможности выбора режимов фракционирования дозы в нейтронной терапии.