Adaptive guaranteed estimation of a constant signal under uncertainty of measurement errors
Автор: Khadanovich D.V., Shiryaev V.I.
Рубрика: Управление в технических системах
Статья в выпуске: 4 т.20, 2020 года.
Бесплатный доступ
In the guaranteed estimation problems under uncertainty relative to disturbances and measurement errors, the admissible sets of their possible values are determined. The solution is chosen due to conditions of guaranteed bounded estimates optimization corresponding to the worst realization of disturbances and measurement errors. The result of the guaranteed estimation is an unimprovable bounded estimate (information set), which turns to be overly pessimistic (reinsurance) if a prior admissible set of measurement errors is too large compared to their realized values. The admissible sets of disturbances and measurement errors can turn to be only rough upper estimates on a short observation interval. The goal of research is the accuracy enhancement problem of guaranteed estimation when measurement errors are not realized in the worst way, i.e. the environment in which the object operates does not behave as aggressively as it is built in a priori data on the permissible set of error values. Research design. The problem of adaptive guaranteed estimation of a constant signal from noisy measurements is considered. The adaptive filtering problem is, according to the results of measurement processing, from the whole set of possible realizations of errors, to choose the one that would generate the measurement sequence. Results. An adaptive guaranteed estimation algorithm is presented. The adaptive algorithm construction is based on a multi-alternative method based on the Kalman filter bank. The method uses a set of filters, each of which is tuned to a specific hypothesis about the measurement error model. Filter residuals are used to compute estimates of realized measurement errors. The choice of the realization of possible errors is performed using a function that has the meaning of the residual variance over a short time interval. Conclusion. The computational scheme of the adaptive algorithm, the numerical example, and comparative analysis of obtained estimates are presented.
Constant signal estimation, guaranteed estimation, adaptive algorithm, bounded estimate, measurement residual
Короткий адрес: https://sciup.org/147233782
IDR: 147233782 | УДК: 51-7 | DOI: 10.14529/ctcr200403
Текст научной статьи Adaptive guaranteed estimation of a constant signal under uncertainty of measurement errors
The estimation problem of a constant signal x from noisy measurements is considered [1]
У к = x + V k , k = 1,2,..., N , (1)
where x e R 1 is a constant value (useful signal), vk e R 1 are the measurement errors. Under natural conditions, the values of measurement errors vk , к = 1, N , are unknown (uncontrolled). A priori information about measurement errors is formalized by choosing a hypothesis about the properties of errors vk . The following hypotheses are traditional.
-
1. The measurement errors vk are random and given by probability density function with known parameters.
-
2. The measurement errors vk are uncertain quantities: vk e V , where V is a given convex set of their possible values.
Acceptance of the hypothesis about the probabilistic nature of measurement errors makes it possible to formulate the problem within the framework of the stochastic approach as the problem of finding the optimal estimate in the mean square sense and to use statistical methods [2]. The most common is the use of the least-squares method (LS) [1, 2], i.e. minimizing a function
N 2
J ( x ) = S ( Ук - x ) , x LS = argmin J ( x ) . k = 1 x
Recurrent algorithms are most widely used in solving problems of processing noisy measurements when an estimate of an unknown quantity is formed by the sequential processing of each available measurement and the results obtained at the previous processing step. The recurrent LS-method is the relations of the Kalman filter (KF) for the considered problem (1) [3, 4]. However, any inaccuracy in the knowledge of the probabilistic characteristics of errors vk can cause divergence of the filtering process [5–8].
However, in many situations, the application of stochastic estimation methods can be difficult: due to the small number of available measurements, based on the results of which the search for the best estimate is carried out, or the absence of probabilistic characteristics of measurement errors. Besides, the assumption about the random nature of measurement errors is not always justified [5, 8]: often it is only known that the measurement errors vk are bounded.
Given a set of possible values of measurement errors, it is possible to formulate the problem within the guaranteed (set-membership approach) as the problem of finding the bounded set of possible values of an unknown quantity [9–26]. In this case, the problem solution is selected from the condition of the optimization of guaranteed bounded estimates corresponding to the worst realization of measurement errors [8, 12, 18, 24]. The advantage of guaranteed estimation methods is the absence of random filtering errors [10–15, 21, 23, 27]. However, the resulting bounded estimate (information set) may turn out to be overly pessimistic (reinsurance) if the set of possible values of measurement errors is too wide [8, 17, 18]. The problem of adaptive algorithm development for guaranteed estimating becomes relevant [28]. The adaptive guaranteed estimation problem is, according to the results of measurement processing, from the whole set of possible realizations of errors, to choose the one that would generate the sequence of measurements [8].
One of the central issues of modern estimation theory [29–32] is the synthesis of adaptive filters enabling of providing a sufficiently accurate estimate of the state vector in the absence of accurate a priori information about disturbances and measurement errors is one of the. In [6, 7, 29, 32], various algorithms for adaptive filtering of stochastic systems with unknown values of the noise covariance matrices are discussed.
This article is focused on the problem of adaptive guaranteed estimation of a constant signal from noisy measurements. The development of an adaptive estimation algorithm is based on a multialternative method based on a Kalman filter bank, which was first proposed in [33] for estimating random processes with unknown constant parameters [34, 35]. This method has found wide application in problems with a multi-alternative description of a system state or process [36–38]. The work continues research [39, 40].
Consider the estimation problem solution of unknown constant signal from a single realization of measurements (1) in the framework of a guaranteed (set-membership) approach. A priori information about the initial value x 0 of a variable and errors vk is represented in the form of admissible sets of the corresponding quantities [9–12, 16–20, 24, 26]
x о e X 0 =[ - x 0 , + x 0 ] , V k e V = [ - v , + v ] , k = 1,2,..., N , (2) where - x , + x are respectively left and right bounds of the set X 0, - v , + v are respectively left and right bounds of the set V .
The result of guaranteed estimation is the construction of the information set X k that is guaranteed to contain an unknown signal x [10–24].
x e Xk =[-xk, + xk ], k = 1,2,..., N.(3)
The information set is defined as follows [18, 23]:
Xk = Xk-1 nX[yk], X0 = X0, k = 1,2,...,N,(4)
where X [ yk ] is the measurement consistent set
X [ yk ] = { x I x = yk - v, v e V}, k = 1,2,..., N.(5)
The presence of the estimate X k (4) is fundamentally important from determining the consistency of a priori information (2) [23]. The algorithm efficiency mainly depends on a priori estimate V which is adequate to the realized errors vk :
-
1. Errors in the set V definition, i.e. a failure of the assumptions (2) when v k t V , can lead to the fact that the information set X k may be empty at some time step k : Xk = 0 . Errors in set X 0 definition can also lead to such a situation.
-
2. If the set V is too wide, then the information set Xk will regularly within the measurement consistent set X [ yk ] : Xk - 1 с X [ yk ] , Xk - i = Xk . In this case, measurement processing is useless, i.e. it does not lead to an increase in the estimation accuracy – a decrease in estimation errors.
Consider an algorithm for solving the guaranteed estimation problem for the case, when a prior admissible set V is too wide, as a result Xk - i = Xk , k = 1,2,....
By following the LS-method and the KF, consider the measurement residual formed as the diffe- rence between the measured value and the estimate obtained at the previous step [4, 8, 9] цk=yk -xk-i, xk-i g Xk-i=[-xk-1,+ xk-i],
x k - i = ( - x k - i + + x k - i ) /2, k = u-. N .
Substituting the measurement equation (1) into this equation, we find that
-
ц k = ek + vk , k = i,2,..., N , (7)
where ek = x - x k - i is the estimation error of unknown signal x .
Thus, the residual ц k (7) corresponding to the current moment of time k is an estimate of the realized measurement error vk , and the estimation error of the measurement error is equal to the estimation error of the signal x .
As for estimation error ek , it is known that ek eX0-i = [_xk-i, + x^], k = i,2,...,N, (8)
where
Xk-i = Xk-i -xk-i, k = i,2,...,N, is the centered set symmetric about zero, 0 e Xk-i.
The estimate (8) is guaranteed and means that the actual estimation error ek can take any value from the set X k l -i .
Taking into account the constraint (8) on the error value ek , the permissible set of measurement errors vk can be represented as
V k = { v I v = ц k - e , v e e X L} = { v I ц k - + xk - i ^ v ^ц k - - xk - i } =
= [цk -+ xk-i, цk --xk-i], k =i,2,-,N.
In the equation for the measurement residual (6) substitute the estimate x0* given a priori for the estimate obtained at the previous time step xk-i цk = yk -x0 = e + vk, k =i,2,-,N, x0 eX0 =[-x 0, + x0 ], x0 =(-x 0 + + x 0 )/2.(ii)
The value e = x - x0
is the error of the initialization of x .
The centered set e el -xо
*
- x 0 ,
+ x 0
—
* x 0
is the set of possible values of errors e (12), symmetric about zero.
Taking into account equations (10) and conditions (11), (13), represent the admissible set of measurement errors in the form vke Vk
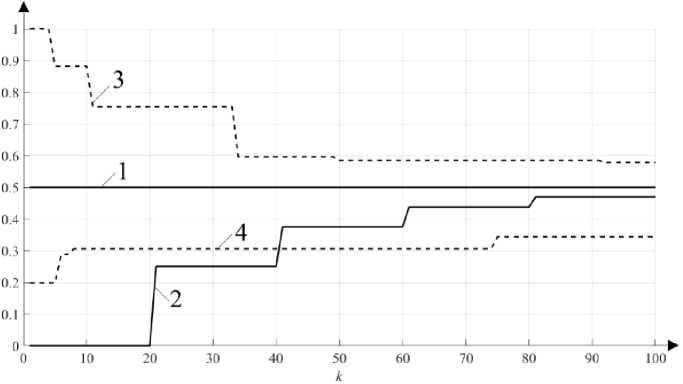
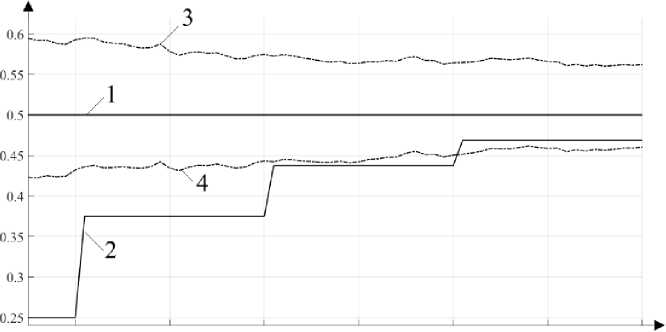
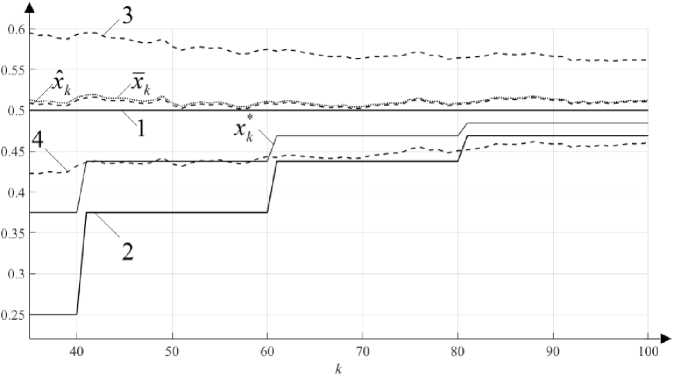
-{ vIHk — ( + x0
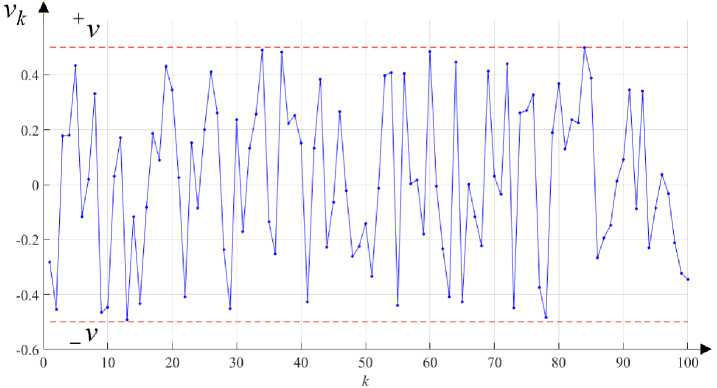
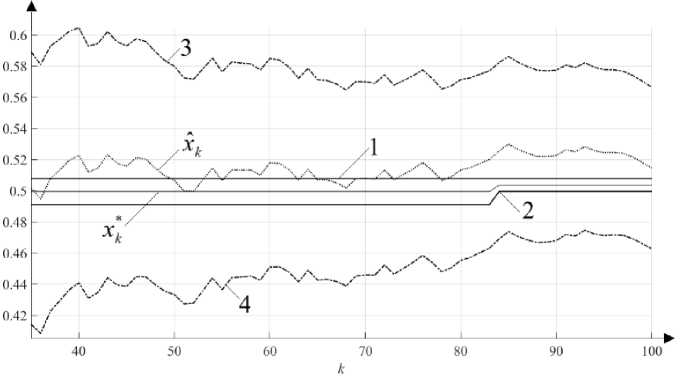
— x0 )< v * — x0 Л k —( +x 0 — x0), Hk—( — xo — * x0 k -1,2,..., N. Thus, the width of the permissible set Vk (14) of measurement errors vk is determined by the width of the permissible set of errors e in setting information about the actual value x (13). Explain this choice. As shown above, if the admissible set V - I v, + v I of errors vk is a priori given too wide, so that X0 с V , then the information set Xk is within the measurement consistent set: Xk—1 с X [yk ] and Xk—1 - Xk. According to the minimax principle, the estimation error ek - e - x — x0 (12) will be the minimum of the maximum possible (minimum in the worst case) at point x0* (11). Be- sides, its value does not depend on measurements yk, k -1, N and is constant over the entire considered time interval. The admissible set (13) of the estimation error e can be represented as the sum of two subsets e еГ xо -x0, 01 + Г0, + xо -x0J. (15) The value and sign of the actual estimation error e are unknown. Therefore, we can talk about accepting one of two hypotheses, a hypothesis H0: e < 0, e e| — x0 — x0, oJ or a hypothesis H1: e > 0, e e|o, + x0 — x0 J . The acceptance of the hypothesis H0 with the fulfillment of conditions eel — xо — x0, 0l leads to a guaranteed result vk e Vk - {v I Hk <v — * x0 k -1,2,..., N. The acceptance of the hypothesis H0 , while e e I 0, + x0 — x* I, leads to the fact that vk £ Vk -{v I Hk < v Vk-{v I Hk—(+ xо— x0 )< v An error in setting the set Vk (17) can lead to the fact that the information set Xk at some time step k may turn out to be empty: Xk - 0 . In this case, further construction of the sets using the filter equations (4), (5) becomes impossible. However, it may turn out that Xk—1 nX[yk] ^0, but the result of the estimation is false x £ Xk. In case of this situation, it is possible (given a priori information (15) about the possible values of estimation errors e e|—x0— x0, oJ - hypothesis H0 and e e|o, +x0— x0 J - hypothesis H1) to solve the guaranteed estimation problem using parallel computations considering the results of the algorithm for different values Vk (16), (17): 1. If, given a hypothesis H0 / H1, it turned out that vk £ Vk at some time step k , then the information set obtained by time step k becomes empty Xk - 0 . Starting from a time step k +1, an alternative hypothesis is taken into account H1 / H0 . 2. If, given a hypothesis H0 / H1, it turned out that vk £ Vk at some time step k but the presence of bounded set Xk ^ 0 does not allow to recognize this situation, then the criterion for choosing a set Vk is the accuracy of the obtained estimates xk*. To characterize the actual quality of estimation, one can use a sequence of a posteriori residuals of measurements [8, 9, 39, 40]. Yk = Ук -xL x*eXk =[-xk, +xk], k =I2,-,N, (18) where xk*is the estimate of unknown signal x obtained by the time step k . Of particular interest is to obtain the best (optimal) estimates xk*. These estimates can be obtained by solving the problem of minimizing the function N Eyk ^ min. (19) k=1 xk eXk Function (19), which is the sum of the squares of a posteriori residuals, carries information about the estimated error of estimation [8, 9]. Therefore, the criterion for choosing the admissible set of realized measurement errors is the accuracy of the obtained point estimates xk*of the signal x for different values of Vk (16), (17). In this case, the algorithm accuracy for the selected set Vk is estimated by averaging over the considered measurement interval. Thus, it is possible to specify the following guaranteed estimation algorithm, which is adaptive to the realized measurement errors. 1. The measurement interval k = 1,..., N is divided into equal l sub-intervals. 2. Two competing hypotheses H0 and H1 are accepted that the estimation errors e model given in the form of a set of their possible values e e|- x0- x0, o] and e e|^0, +x0 - x0 ] respectively, rather accurately describes the behavior of actual estimation errors on the measurement interval y1, y2,..., yl . 3. Following the accepted hypotheses, the admissible sets of measurement errors are calculated (16) and (17), respectively. We will consider the results of the estimation algorithm for different admissible sets of measurement errors. 4. The estimate of the signal x obtained on this measurement interval will be denoted xl*and will be found by the criterion of the minimum squared residuals (19), comparing the results of the algorithm for different admissible sets of measurement errors. 5. For the next measurement interval yl+1, yl+2,..., yl+/ as a priori estimate of the signal x, we will consider the estimate obtained from measurements at the last time steps l: x0= x*, X0= Xl. The measurement processing on the interval k = l +1, l +l is carried out in the same way as the measurement processing on the interval k = 1, l. The application of the algorithm does not require storing l measurements, but only calculating and storing estimates with the width of the measurement interval equal to l . Represent a multi-alternative model of the algorithm in the following form. Algorithm 1 Step 0. Determine the admissible sets x0e X0 = | -x0, +x0] , vk e V = | -v, +v], k = 1, l, l« N. Step 1. Define k = 1. Step 2. Calculate x0 following (11). Accept the hypothesis H0: e e | - x0- x0, o] . Step 3. Calculate цk following (10) and the admissible set of measurement errors vk following (16). Step 4. Calculate Xk following (4), (5). Step 5. If Xk=0, go to Step 2 of Algorithm 2. Otherwise, go to Step 6. Step 6. Calculate yk following (18). Step 7. Define k = k +1 go to Step 3. If k = l, go to Step 8. l Step 8. CalculateZy 2. k=1 ll Step 9. If the value Zy2 corresponding to Step 8 of Algorithm 1 is less than the value Zy2 cor-k=1 k=1 responding to Step 8 of Algorithm 2, define k = l +1, X0 = Xl and go to Step 2. Otherwise, go to Step 2 of Algorithm 2. Algorithm 2 Step 0. Determine the admissible sets x0е X0= [_x0, +x0J , vk е V = [_v, +vJ, k = 1, l, l« N. Step 1. Define k = 1. Step 2. Calculate x0 following (11). Accept the hypothesis H1: e е ^0, +x0- x0 J . Step 3. Calculate цk following (10) and the admissible set of measurement errors vk following (17). Step 4. Calculate Xk following (4), (5). Step 5. If Xk = 0, go to Step 2 of Algorithm 1. Otherwise, go to Step 6. Step 6. Calculate yk following (18). Step 7. Define k = k +1 go to Step 3. If k = l, go to Step 8. l Step 8. CalculateZy k. k=1 ll Step 9. If the value Zy2 corresponding to Step 8 of Algorithm 2 is less than the value Zy2 cor-k=1 k=1 responding to Step 8 of Algorithm 1, define k = l +1, X0= Xl and go to Step 2. Otherwise, go to Step 2 of Algorithm 1. The problem of constant signal estimation from noisy measurements is considered yk = x + vk, k = 1,..., N. (20) The true value is x = 0.5, the number of measurements is N = 100. The noisy measurements yk (20) and measurement errors vk are shown in Fig. 1. The measurement errors are assumed to be zero mean Gaussian white noise sequence with standard deviation оv = 0.17. The prior admissible sets are taken as follows: X0 =[_x0, + x0J = [-1, 1], V = [_v, +v! = [ 30v, 30v]. As Fig. 1b shows, the realization of measurement errors is such that |vk | ^ 3ov. a) b) Fig. 1. The processes considered in the example: a – noisy measurements yk ; b – measurement errors vk The measurement interval was divided into 5 equal sub-intervals. According to the results of measurement processing, the information set of possible values of the signal x is obtained (Fig. 2) x g XN =[0.4688, 0.5], xN = 0.4844, k g[80, 100]. The information set of possible values of the signal x computed by “non-adaptive” filter is (Fig. 2) x g XN =[0.3431, 0.5779], x— = 0.4605, k g[92, 100]. Fig. 2. Bounded estimates of the signal x: 1, 2 – respectively the upper and lower bounds of the information set computed by the adaptive guaranteed algorithm; 3, 4 – respectively the upper and lower bounds of the information set computed by “non-adaptive” algorithm The maximum possible error of the adaptive filter is max |x - c = 0.0312, and that of “non- CG XN adaptive” filter becomes max lx - cl = 0.1569. As a quantitative characteristic of the efficiency of CGX— ' ' X the proposed adaptive estimation algorithm, consider the ratio 5д, = —— -100% of intervals N X0 XN =[-xN, + xN ] and X0 =[-x0, + x0 ] . The quantity 5 shows what part of the prior uncertainty is the information set [41]. The information set computed by the adaptive guaranteed algorithm does not exceed 2% (5 = 1.56) of the prior uncertainty value, while the information set computed by the “non-adaptive” guaranteed algorithm exceeds 11% (5 = 11.74) of the prior uncertainty value. Application of the Kalman Filter Recurrence equations of LSE [3, 8] xk = xk-1 +Pkr-1(Ук- xk-1), k = I2,™,N, (21) Pk =( P--1 + r-1)-1. (22) As mentioned above, equations (21), (22) are the KF equations for the considered problem (20). The variance of measurement errors is known: r = о2. Initial conditions for the KF are: x g N(0, p0), x) = 0, P0 = 9. From a comparison of the results of the adaptive guaranteed estimation and the KF (Fig. 3, Table 1), it follows that the implementation of the adaptive guaranteed estimation algorithm made it possible to reduce the initial uncertainty in the knowledge of the signal x by 64 times, and the use of the Kalman filter – by 20 times. Table 1 k Adaptive guaranteed algorithm The Kalman Filter max x - c ceXk 1 1 5 k max x - c ce[-34p ,3 4p ] 5 k 20 0.5 25 0.1330 11.33 40 0.25 12.5 0.0928 8.04 60 0.125 6.25 0.0726 6.57 80 0.0625 3.125 0.0643 5.7 100 0.0312 1.56 0.0620 5.09 40 50 60 70 80 90 100 к Fig. 3. Bounded estimates of the signal x: 1, 2 – respectively the upper and lower bounds of the information set; 3, 4 - respectively the upper +3a and lower -3a bounds of the confidence set computed by the KF Characteristics of bounded estimates For the relative errors of the Kalman estimate xˆN and the estimate x*N of the adaptive guaranteed algorithm, respectively, we have (Fig. 4, Table 2) ------1x - xN' .----, -100% = 17.74%, x .xN .100% = 50%. max x - c max x - c cG[-3 4pN ,3 M ] cexn Fig. 4. Point estimates of the signal x: 1, 2 – respectively the upper and lower bounds of the information set; 3, 4 - respectively the upper +3a and lower -3a bounds of the confidence set computed by the KF Table 2 Characteristics of point estimates k The Kalman filter Adaptive guaranteed algorithm Mean type method A xk estimation error 1 x-xkl * xk estimation error x—xk 1k xk = ,X y ki=1 estimation error x—xk 20 0.5197 0.0197 0.25 0.25 0.5265 0.0265 40 0.5124 0.0124 0.375 0.125 0.5157 0.0157 60 0.5090 0.0090 0.4375 0.0625 0.5112 0.0112 80 0.5074 0.0074 0.4688 0.0312 0.5090 0.0090 100 0.5110 0.0110 0.4844 0.0156 0.5124 0.0124 The relative error of the Kalman estimate xˆN turned out to be 3 times less than the relative error of the estimate x*N of the adaptive guaranteed algorithm. The Kalman estimate turns out to be more accurate since the real probability distribution law of measurement errors vk is Gaussian. The estimate of the guaranteed algorithm is selected based on the worst realization of measurement errors. In the case of a single realization of measurements {yk}N1, the solution of the guaranteed estimation problem, when the estimate is a point which is equidistant from bounds of the information set (middle point of the interval), is nonrational [41]. In the considered example, the true value of the signal x is on the border of the information set. However, in practice, such a situation cannot be recognized. Consider the measurement errors vk in terms of uniformly distributed in the interval [-v, v] white noise at level of about v = 0.5 (Fig. 5). The prior admissible sets are Xо =[— xo,+Xo] = [-1, 1], V = [—v, +v] = [-0.5, 0.5]. Initial conditions for the KF are: x e N(0, p0), x0= 0, p0= 1 r = ( 0.5/3)2. Fig. 5. Measurement errors vk As Fig. 5 shows, the realization of measurement errors is such that at some time steps | vk | ~ 0,5. A comparison of the results of “non-adaptive” guaranteed estimation and the KF is shown in Fig. 6 and Table. 3. Fig. 6. Bounded estimates of the signal x: 1, 2 – respectively the upper and lower bounds of the information set; 3, 4 - respectively the upper +3a and lower -3a bounds of the confidence set computed by the KF Table 3 Characteristics of bounded estimates k Guaranteed algorithm The Kalman filter max x - cl ce Xk1 1 8 k max x - c ce[-34p ,3 4p J 8 k 20 0.0653 3.65 0.1463 11.54 40 0.009 0.83 0.1046 8.19 60 0.009 0.83 0.0848 6.69 80 0.009 0.83 0.0713 5.8 100 0.0077 0.41 0.0664 5.19 The information set XN =|__xN, +xN J computed by the guaranteed algorithm does not exceed 1% (8 = 0.41) of the prior uncertainty value, while the confidence set ^ 3vpN , 3 VPN J computed by the KF exceeds 5% (8 = 5.19) of the prior uncertainty value. The maximum possible error of the guaranteed estimate is max lx - cl = 0.0077, which is almost 10 times less than the maximum possible error of ce Xn 1 1 the Kalman estimate, which is max |x - cl = 0.0664. In addition, the true value of the signal x ce[-3-Jpn ,3-JpN J may not belong to the confidence set: x £ ^ 3.JpN, 3^ pN J . Thus, in the case when the admissible set of measurement errors V = [-v, +vJ is adequate to the realized measurement errors so that the measurement errors can take values on the set bound or close to its bound, the guaranteed estimation errors are minimal. For the considered realization of measurement errors (Fig. 5), at time steps k = 13,34,84 the values of measurement errors are closest to the boundary values. At these time steps, the guaranteed algorithm provides the most accurate estimates. In this case, the application of adaptive methods is not required. The article has proposed a solution to the problem of adaptive guaranteed estimation for a constant signal from noisy measurements. It is based on a multi-alternative method when a set (bank) of filters is used, with each of which tuned to a specific hypothesis about possible realizations of measurement errors. Filter residuals are used to compute estimates of realized measurement errors. Choosing the possi- ble implementation of errors is made by using a composed function that makes sense of the variance of residuals over a short time interval. Numerical simulations have confirmed the effectiveness of the proposed adaptive guaranteed estimation algorithm. Exploring further the issues: the statement of the necessary criterion for an opportunity of adaptive adjustment of the algorithm; properties of the adaptive filter on short time intervals; generalization of obtained results to the multidimensional case in the presence of unknown bounded disturbances. One of the promising directions for further research is the development of an algorithm that combines the guaranteed estimation algorithm and the Kalman filter. The work was supported by Act 211 Government of the Russian Federation, contract No. 02.A03.21.0011. 1. Fomin V.N. Rekurrentnoye otsenivaniye i adaptivnaya fil'tratsiya [Recurrent Estimation and Adaptive filtering]. Moscow, Nauka Publ., 1984, 288 p. 2. Sorenson H.W. Least-squares estimation: from Gauss to Kalman. IEEE Spectrum, 1970, vol. 7, iss. 7, pp. 63–68. 3. Kalman R.E. A New Approach to Linear Filtering and Prediction Problems. Transactions of the ASME – Journal of Basic Engineering, 1960, vol. 82, pp. 35–45. 4. Stepanov O.A. Kalman Filtering: Past and Present. An Outlook from Russia. Gyroscopy and Navigation, 2011, vol. 2, iss. 2, pp. 99–110. 5. Kalman R.Е. Identification of noisy systems. Russian Mathematical Surveys, 1985, vol. 40, iss. 4, pp. 25–42. 6. Jazwinski A.H. Adaptive filtering. Automatica, 1969, no. 4, pp. 475–485. 7. Mehra R.K. Approaches to adaptive filtering. IEEE Transactions on Automatic Control, 1972, vol. 17, iss. 5, pp. 693–698. 8. Malyshev V.V., Kibzun A.I. Analiz i sintez vysokotochnogo upravleniya letatel'nymi apparatami [Analysis and Synthesis of High-Precision Control of Aircrafts]. Moscow, Mashinostroenie Publ., 1987, 302 p. 9. Kantorovich L.V. [On Some New Approaches to Computational Methods and Observation Processing]. Siberian Mathematical Journal, 1962, vol. 3, no. 5, pp. 701–709. (in Russ.) 10. Schweppe F. Recursive state estimation: Unknown but bounded errors and system input. IEEE Transactions on Automatic Control, 1968, vol. 13, iss.1, pp. 22–28. 11. Bertsekas D., Rhodes I. Recursive state estimation for a set-membership description of uncertainty. IEEE Transactions on Automatic Control, 1971, vol. 16, iss. 2, pp. 117–128. 12. Kats I.Ya., Kurzhanski A.B. [Minimax Multi-Step Filtering in Statistically Uncertain Situations]. Automation and Remote Control, 1979, vol. 39, iss. 11, pp. 1643–1650. (in Russ.) 13. Bakan G.M. [Non-Statistical Statement and Solution of One Filtering Problem]. Automation and Remote Control, 1983, vol. 44, iss. 9, pp. 1125–1136. (in Russ.) 14. Kane V.M. Optimizatsiya sistem upravleniya po minimaksnomu kriteriyu [Optimization of Control Systems According to the Minimax Criterion]. Moscow, Nauka Publ., 1985, 258 p. 15. Chernousko F.L. [Guaranteed Uncertainty Estimates Using Ellipsoids]. Soviet Mathematics. Doklady, 1980, vol. 251, no. 1, pp. 51–54. (in Russ.) 16. Kurzhansky A.B. [The Identification Problem – Theory of Guaranteed Estimates]. Automation and Remote Control, 1991, vol. 52, iss. 4, pp. 447–465. (in Russ.) 17. Shiryaev V.I. [Synthesis of Control of Linear Systems in Incomplete Information]. Journal of Computer and Systems Sciences International, 1994, no. 3, pp. 229–237. (in Russ.) 18. Shiryaev V.I. [Control Algorithms for Dynamical Systems under Uncertainty]. Mekhatronica, 2001, no. 8, pp. 2–5. (in Russ.) 19. Kuntsevich V.M. Upravleniye v usloviyakh neopredelennosti: garantirovannyye rezul'taty v zadache upravleniya i identifikatsii [Control under Uncertainty: Guaranteed Results in Control and Identification Problems]. Kiev, Naukova Dumka Publ., 2006, 264 p. 20. Polyak B.T., Topunov M.V. Filtering under Nonrandom Disturbances: the Method of Invariant Ellipsoids. Doklady Mathematics, 2008, vol. 77, no.1, pp. 158–162. (in Russ.) 21. Matasov A.I. Metod garantiruyushchego otsenivaniya [Guaranteed Estimation Method]. Moscow, Moscow State University Publ., 2009, 100 p. 22. Nazin S.A., Polyak B.T. Ellipsoid-based parametric estimation in the linear multidimensional systems with uncertain model description. Automation and Remote Control, 2007, vol. 68, iss. 6, pp. 993–1005. (in Russ.) 23. Salnikov N.N. Estimation of State and Parameters of Dynamic System with the Use of Ellipsoids at the Lack of a Priori Information on Estimated Quantities. Journal of Automation and Information Sciences, 2014, no. 2, pp. 144–156. (in Russ.) 24. Shalygin A.S., Lysenko L.N., Tolpegin O.A. Modeling Techniques of Situational Control of the Movement of Unmanned Aerial Vehicles. Eds. A.V. Nozdrachev and L.N. Lysenko. Moscow, Mashinostroenie Publ., 2012, 584 p. 25. Le V.T.H., Stoica C., Alamo T., Camacho E.C., Dumur D. Zonotopes: from Guaranteed Stateestimation to Control. Wiley-ISTE, 2013, 335 p. 26. Blanchini F., Miani S. Set-Theoretic Methods in Control. Birkhauser, 2015, 630 p. 27. Elyasberg P.E. Measurement information: how much is it needed? How to process it? Moscow, Nauka Publ., 1983, 209 p. 28. Koscheev A.S., Kurzhansky A.B. [Adaptive Estimation of Multistep Systems Evolution under Uncertainty]. Engineering Cybernetics, 1983, no. 2, pp. 72–93. (in Russ.) 29. Barabanov A.E. Linear filtering with adaptive adjustment of the disturbance covariation matrices in the plant and measurement noise. Automation and Remote Control, 2016, vol. 77, pp. 21–36. 30. Gritsenko N.S., Gusarov A.I., Loginov V.P., Sevastyanov K.K. [Adaptive Estimation. Part 1]. Zarubezhnaja Radioelektronika, 1983, no. 7, pp. 3–27. (in Russ.) 31. Pervachev S.V., Perov A.I. Adaptivnaya fil'tratsiya soobshcheniy [Adaptive Message Filtering]. Moscow, Radio i svyaz Publ., 1991, 160 p. 32. Kogan M.M. Optimal estimation and filtration under unknown covariances of random factors. Automation and Remote Control, 2014, vol. 75, iss. 11, pp. 1964–1981. 33. Magill D.T. Optimal Adaptive Estimation of Sampled Stochastic Processes. IEEE Transactions on Automatic Control, 1965, vol. 10, iss. 4, pp. 434–439. 34. Lainiotis D.G. Partitioning: A unifying framework for adaptive systems, I: Estimation. Proceedings of the IEEE, 1976, vol. 64, iss. 8, pp. 1126–1143. 35. Koshaev D.A. Kalman filter-based multialternative method for fault detection and estimation. Automation and Remote Control, 2010, vol. 71, pp. 790–802. 36. Dmitriev S.P., Stepanov O.A. [Multialternative filtering in navigation information processing problem]. Radioengineering, 2004, no. 7, pp. 11–17. (in Russ.) 37. Fisher K.A., Maybeck P.S. Multiple model adaptive estimation with filter spawning. IEEE Transactions on Aerospace and Electronic Systems, 2002, vol. 38, iss. 3, pp. 755–768. 38. Rong Li X., Jilkov V.P. Survey of maneuvering target tracking. Part V. Multiple-model methods. IEEE Transactions on Aerospace and Electronic Systems, 2005, vol. 41, iss. 4, pp. 1255–1321. 39. Khadanovich D.V., Shiryaev V.I. On the estimation of measurement errors in linear dynamical systems. Proceedings of 2016 3rd Russian Conference “Mathematical Modeling and Information Technologies” (MMIT 2016), 2016, vol. 1825, pp. 35–43. 40. Khadanovich D.V., Shiryaev V.I. To the Problem of Measurement Errors Estimation in Control Systems with Incomplete Information. Bulletin of South Ural State University. Ser. Computer technologies, automatic control, radioelectronics, 2018, vol. 18, no. 4, pp. 25–40. (in Russ.) 41. Sheludko A.S., Shiryaev V.I. Minimax Filtering Algorithm for One-Dimensional Chaotic Process. Mekhatronika, Avtomatizatsiya, Upravlenie, 2014, no. 5, pp. 8–12. (in Russ.)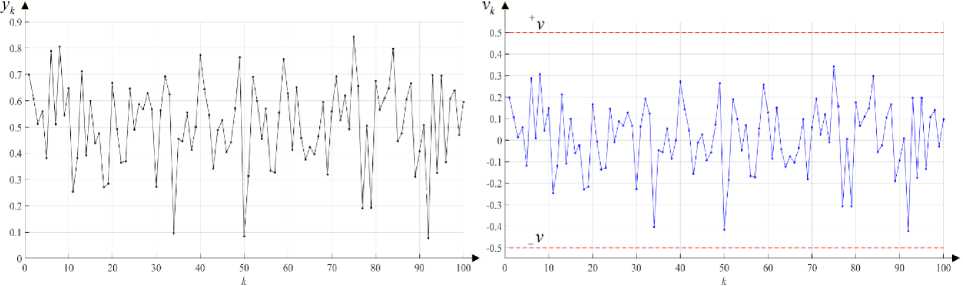
Список литературы Adaptive guaranteed estimation of a constant signal under uncertainty of measurement errors
- Fomin V.N. Rekurrentnoye otsenivaniye i adaptivnaya fil'tratsiya [Recurrent Estimation and Adaptive filtering]. Moscow, Nauka Publ., 1984, 288 p.
- Sorenson H.W. Least-squares estimation: from Gauss to Kalman. IEEE Spectrum, 1970, vol. 7, iss. 7, pp. 63-68.
- Kalman R.E. A New Approach to Linear Filtering and Prediction Problems. Transactions of the ASME - Journal of Basic Engineering, 1960, vol. 82, pp. 35-45.
- Stepanov O.A. Kalman Filtering: Past and Present. An Outlook from Russia. Gyroscopy and Navigation, 2011, vol. 2, iss. 2, pp. 99-110.
- Kalman R.E. Identification of noisy systems. Russian Mathematical Surveys, 1985, vol. 40, iss. 4, pp. 25-42.
- Jazwinski A.H. Adaptive filtering. Automatica, 1969, no. 4, pp. 475-485.
- Mehra R.K. Approaches to adaptive filtering. IEEE Transactions on Automatic Control, 1972, vol. 17, iss. 5, pp. 693-698.
- Malyshev V.V., Kibzun A.I. Analiz i sintez vysokotochnogo upravleniya letatel'nymi apparatami [Analysis and Synthesis of High-Precision Control of Aircrafts]. Moscow, Mashinostroenie Publ., 1987, 302 p.
- Kantorovich L.V. [On Some New Approaches to Computational Methods and Observation Processing]. Siberian Mathematical Journal, 1962, vol. 3, no. 5, pp. 701-709. (in Russ.)
- Schweppe F. Recursive state estimation: Unknown but bounded errors and system input. IEEE Transactions on Automatic Control, 1968, vol. 13, iss.1, pp. 22-28.
- Bertsekas D., Rhodes I. Recursive state estimation for a set-membership description of uncertainty. IEEE Transactions on Automatic Control, 1971, vol. 16, iss. 2, pp. 117-128.
- Kats I.Ya., Kurzhanski A.B. [Minimax Multi-Step Filtering in Statistically Uncertain Situations]. Automation and Remote Control, 1979, vol. 39, iss. 11, pp. 1643-1650. (in Russ.)
- Bakan G.M. [Non-Statistical Statement and Solution of One Filtering Problem]. Automation and Remote Control, 1983, vol. 44, iss. 9, pp. 1125-1136. (in Russ.)
- Kane V.M. Optimizatsiya sistem upravleniyapo minimaksnomu kriteriyu [Optimization of Control Systems According to the Minimax Criterion]. Moscow, Nauka Publ., 1985, 258 p.
- Chernousko F.L. [Guaranteed Uncertainty Estimates Using Ellipsoids]. Soviet Mathematics. Doklady, 1980, vol. 251, no. 1, pp. 51-54. (in Russ.)
- Kurzhansky A.B. [The Identification Problem - Theory of Guaranteed Estimates]. Automation and Remote Control, 1991, vol. 52, iss. 4, pp. 447-465. (in Russ.)
- Shiryaev V.I. [Synthesis of Control of Linear Systems in Incomplete Information]. Journal of Computer and Systems Sciences International, 1994, no. 3, pp. 229-237. (in Russ.)
- Shiryaev V.I. [Control Algorithms for Dynamical Systems under Uncertainty]. Mekhatronica, 2001, no. 8, pp. 2-5. (in Russ.)
- Kuntsevich V.M. Upravleniye v usloviyakh neopredelennosti: garantirovannyye rezul'taty v zadache upravleniya i identifikatsii [Control under Uncertainty: Guaranteed Results in Control and Identification Problems]. Kiev, Naukova Dumka Publ., 2006, 264 p.
- Polyak B.T., Topunov M.V. Filtering under Nonrandom Disturbances: the Method of Invariant Ellipsoids. Doklady Mathematics, 2008, vol. 77, no.1, pp. 158-162. (in Russ.)
- Matasov A.I. Metod garantiruyushchego otsenivaniya [Guaranteed Estimation Method]. Moscow, Moscow State University Publ., 2009, 100 p.
- Nazin S.A., Polyak B.T. Ellipsoid-based parametric estimation in the linear multidimensional systems with uncertain model description. Automation and Remote Control, 2007, vol. 68, iss. 6, pp. 993-1005. (in Russ.)
- Salnikov N.N. Estimation of State and Parameters of Dynamic System with the Use of Ellipsoids at the Lack of a Priori Information on Estimated Quantities. Journal of Automation and Information Sciences, 2014, no. 2, pp. 144-156. (in Russ.)
- Shalygin A.S., Lysenko L.N., Tolpegin O.A. Modeling Techniques of Situational Control of the Movement of Unmanned Aerial Vehicles. Eds. A.V. Nozdrachev and L.N. Lysenko. Moscow, Mashinostroenie Publ., 2012, 584 p.
- Le V.T.H., Stoica C., Alamo T., Camacho E.C., Dumur D. Zonotopes: from Guaranteed State-estimation to Control. Wiley-ISTE, 2013, 335 p.
- Blanchini F., Miani S. Set-Theoretic Methods in Control. Birkhauser, 2015, 630 p.
- Elyasberg P.E. Measurement information: how much is it needed? How to process it? Moscow, Nauka Publ., 1983, 209 p.
- Koscheev A.S., Kurzhansky A.B. [Adaptive Estimation of Multistep Systems Evolution under Uncertainty]. Engineering Cybernetics, 1983, no. 2, pp. 72-93. (in Russ.)
- Barabanov A.E. Linear filtering with adaptive adjustment of the disturbance covariation matrices in the plant and measurement noise. Automation and Remote Control, 2016, vol. 77, pp. 21-36.
- Gritsenko N.S., Gusarov A.I., Loginov V.P., Sevastyanov K.K. [Adaptive Estimation. Part 1]. Zarubezhnaja Radioelektronika, 1983, no. 7, pp. 3-27. (in Russ.)
- Pervachev S.V., Perov A.I. Adaptivnaya fl'tratsiya soobshcheniy [Adaptive Message Filtering]. Moscow, Radio i svyaz Publ., 1991, 160 p.
- Kogan M.M. Optimal estimation and filtration under unknown covariances of random factors. Automation and Remote Control, 2014, vol. 75, iss. 11, pp. 1964-1981.
- Magill D.T. Optimal Adaptive Estimation of Sampled Stochastic Processes. IEEE Transactions on Automatic Control, 1965, vol. 10, iss. 4, pp. 434-439.
- Lainiotis D.G. Partitioning: A unifying framework for adaptive systems, I: Estimation. Proceedings of the IEEE, 1976, vol. 64, iss. 8, pp. 1126-1143.
- Koshaev D.A. Kalman filter-based multialternative method for fault detection and estimation. Automation and Remote Control, 2010, vol. 71, pp. 790-802.
- Dmitriev S.P., Stepanov O.A. [Multialternative filtering in navigation information processing problem]. Radioengineering, 2004, no. 7, pp. 11-17. (in Russ.)
- Fisher K.A., Maybeck P.S. Multiple model adaptive estimation with filter spawning. IEEE Transactions on Aerospace and Electronic Systems, 2002, vol. 38, iss. 3, pp. 755-768.
- Rong Li X., Jilkov V.P. Survey of maneuvering target tracking. Part V. Multiple-model methods. IEEE Transactions on Aerospace and Electronic Systems, 2005, vol. 41, iss. 4, pp. 1255-1321.
- Khadanovich D.V., Shiryaev V.I. On the estimation of measurement errors in linear dynamical systems. Proceedings of 2016 3rd Russian Conference "Mathematical Modeling and Information Technologies" (MMIT 2016), 2016, vol. 1825, pp. 35-43.
- Khadanovich D.V., Shiryaev V.I. To the Problem of Measurement Errors Estimation in Control Systems with Incomplete Information. Bulletin of South Ural State University. Ser. Computer technologies, automatic control, radioelectronics, 2018, vol. 18, no. 4, pp. 25-40. (in Russ.)
- Sheludko A.S., Shiryaev V.I. Minimax Filtering Algorithm for One-Dimensional Chaotic Process. Mekhatronika, Avtomatizatsiya, Upravlenie, 2014, no. 5, pp. 8-12. (in Russ.)


