Adaptive Modulation and Coding with Channel State Information in OFDM for WiMAX

Published Online December 2014 in MECS

Worldwide interoperability for microwave access (WiMAX) [1] is specifically popular in wireless applications due to its opposition to patterns of interference and degradation (multipath and delay spread) [2]. A transmitted symbol may reach the receiver on the other symbol period and induces inter symbol interference (ISI) [3]. At higher data rates, the symbol time is shorter; hence, it assumes merely a small delay to induce ISI. Equalization [3] is the formal method for handling with ISI but at high data rates need an excessive amount of processing power. OFDM (orthogonal frequency division multiplexing) [4] has transformed into the best solution for mitigating ISI in broadband systems, including WiMAX to lend different guard intervals. Guard interval removes ISI and ICI (inter carrier interference) [5] by maintaining orthogonality among all sub carriers.

OFDMA (orthogonal frequency division multiple access) [6] associated with adaptive modulation and coding (AMC) techniques [7] to enhance throughput [8], spectral efficiency [9] and BER performance of wireless communication system by adjusting transmission parameters like modulation code-rates [10] and power on the basis of the channel state adaptively. When adaptive transmission [11] is employed in OFDM system, the transmission parameters of every subcarrier are adapted to each subchannel. To acquire a different code rate for every single subcarrier, rate-compatible punctured convolutional (RCPC) code [12] is employed. Received signal-to-noise ratio (SNR) is applied to measure of the subchannel state to choose a suitable code-rate for every subcarrier.

Transmit power and modulation for each subcarrier is determined for reduction of the adaptive algorithm. LSE [13], MMSE [14] and LMMSE [15] channel estimators are accustomed to give randomly varying channel state information (CSI) [15] to the transmitter by way of a feedback, as shown in Fig. 1. The main algorithm that will be enhanced in this paper is the linear minimum mean square error (LMMSE) for OFDM systems and its low rank version. The proposed channel estimation method requires the statistic knowledge of the channel in advance. Generally, the current channel estimation methods can be classified into two categories. The first one is based on the pilots, and the second one is based on blind channel estimation which does not use pilots and are not suitable for applications with fast varying fading channels. And most useful communication systems nowadays adopt pilot arrangement based channel estimation, for these reasons, this work studies the first category.

The rest of this paper is organized as follows. We introduce the system model in Section II. We present an analytical procedure of channel estimators such as LS, MMSE, LMMSE, Lr-LMMSE algorithms in Section III. The motive behind the integration of adaptive modulation and coding (AMC) technique with WiMAX PHY is presented in Section IV. Simulation results are noted in Section V and finally we write the conclusions drawn from the simulation results in Section VI.

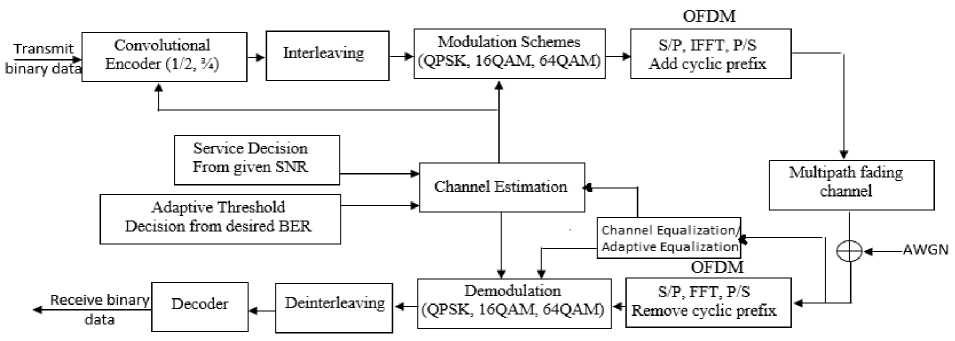
Fig. 1. A basic OFDM-AMC system model.

• II.    Ofdm Transceiver System Model

Recently, OFDM is principally employed in broadband wireless access due to its robustness against multipath, maximizes throughput, robustness against narrowband interference, establishes single frequency network, frequency diversity. In OFDM, the sub carriers are not separated but overlapped orthogonally. As a result of this overlapping, the bandwidth is significantly much more efficiently employed than in the classical multicarrier systems. Theoretically, M-ary digital modulation schemes use OFDM that can accomplish a bandwidth efficiency such as log ^M bits / s h z (where M is the modulation scheme size).

As shown in Fig. 1, in the transmitter section, a convolutional encoder first encodes the binary input data. Coded bits are sent to interleaving and then the binary values are represented on quadrature amplitude modulation (QAM) values. To be able to adjust the signal in the receiver for a possible phase drift, pilot carriers can be inserted. In the Serial to Parallel block, the serial QAM input symbol-stream is transformed into a parallel stream with width equal to the number of sub-carriers. These parallel symbols are modulated onto the sub carriers by applying the Inverse Fast Fourier Transform. Note that in order to get an output spectrum with a relative low out-of-band radiation, the size of the IFFT can be chosen larger than the amount of sub carriers that's actually spent to transmit the data. Following the IFFT block, the parallel output is converted back again to serial and guard interval, cyclic prefix of the time domain samples, is appended to eradicate ISI. IEEE 802.16+ grants the insertion of guard time intervals of several lengths such as 0.25, 0.125, 0.0625 and 0.03125 are lent to the WiMAX symbol earlier it is transmitted. The guard interval is more than the maximum delay time and then the inserted guard interval signal is D/A converted and passed through frequency selective fading channels. In the receivers, the guard interval is removed and the opposite processing is carried out to transmitter like time samples are converted by the FFT into complex symbols. The complex symbol is demodulated adaptively using adaptive modulation level information. Demodulated symbols are block deinterleved. These bits are forwarded to Viterbi decoder. Decoded bits are going to be assigned to a specific user and then extracted utilizing the required bit rate information of the user.

• III.    Channel Estimation

• 3.1    LSE channel estimation

3.2 MMSE channel estimation

Channel estimation is a method to characterize the impact of the physical medium on the input sequence. The key aim of channel estimation is to evaluate the impact of the channel on known or partially known group of transmittances. OFDM systems are specifically equipped for channel estimation. The sub carriers are closely spaced. The channel is estimated on the basis of the training sequence that will be known to both transmitter and receiver. The receiver can employ the known training bits and the respective received samples for estimating the channel.

LSE estimator reduces the square error between estimation and detection to estimate channel h[m]. In matrix form, the actual output can be written as y=Xh and the error is e= ( y — y ) is the expected output. The square error (S) can be defined as [13]

5 ^e |2

= (У - У )2= (У — У )*( У — У) t= (У — Xh )*( У — Xh) t where t stands for the complex transpose of matrix. The equation can be minimized by taking its derivative w.r.t h and equating it corresponding to zero. The final equation is [13],

h = (Xт X)—1 Xt у          (2)

where h = hls = X^-1y. This equation can be implemented on SISO as well as MIMO systems.

The MMSE estimator minimizes the mean-square error. Mean square error = mean ( y — y ) 2 = E ( y — y ) 2 . Notion of expected value and correlation can be utilized to derive the equations for locating the channel response. The estimated channel is [14]

SNR = Ex ; |/ 7 ,          (9)

we obtain a simplified estimator

г              в Y^—1 ^

^h = ^R hh I ^R hh ⁺ „_Mn ¹ I   ^h ls .

^     SNR )

H mmse = F *( R gY * R yY "‘* Y ),        (3)

Where, Ryy = X * F * F' * X ' + Variance of the noise * Identity matrix. The equation can be used for both ISO along with MIMO systems.

3.3 LMMSE channel estimation

The LMMSE estimate of the channel attenuations h , from the received data y and the transmitted symbols X is [14]

Where в = Ex 2| E\ 1/ x_k\ is a constant depending on the signal constellation. In the case of 16-QAM transmission, в = 17 / 9. Because X is no longer a factor in the matrix calculation, no inversion is needed when the transmitted data in X changes. Furthermore, if R hh and SNR are known before hand or are set to fixed nominal values, the matrix

R

hh

+

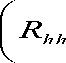
в

SNR

— 1

where

I

= R hh ( R hh + 7 h)^—1)-¹

;  _ Y —1-1, —   y 0   ^y 1          yN —1

s = X y =    ^,_,

L ^x 0   y 1         x N — 1

needs to be calculated only once. Under these conditions the estimation requires N multiplications per subcarrier. To further reduce the complexity of the estimator, we proceed with low-rank approximations in the next section.

3.4 Optimal Low -rank Approximation

The optimal rank reduction of the estimator in (10), using the singular value decomposition (SVD), is obtained by exclusion of base vectors corresponding to the smallest singular values. We denote the SVD of the channel correlation matrix

is the least-squares (LS) estimate of h , 7 2 is the variance of the additive channel noise, and the covariance matrices are

R hh = D N D H

Rhh = E {hhH}

Rhh, = E { hh*is"}

RM. = E { h„V}

h = D N D¹¹ h_b

where N is a diagonal matrix containing the values

The LMMSE estimator (4) is of considerable complexity, since a matrix inversion is needed every time the training data in X changes. We reduce the complexity of this estimator by averaging over the transmitted data [10], i.e. we replace the term ( XX^h ) ^{— 1} in (4) with its expectation E ( XX^h ) ^{— 1} . Assuming the same signal constellation on all tones and equal probability on all constellation points, we get E ( XX^h ) ^{— 1} = E | 1/ x_k |²1 , where I is the identity matrix. Defining the average signal-to-noise ratio as

Y

k k Y + JL ’ k SNR

k = 0,1,2,...N-1

on its diagonal. The best rank -p approximation of the estimator in (10) then becomes

/ z p = U

^N p

U ^Hh ^ˆ ls

Where А_р is the upper left px p corner of A . Viewing the unitary matrix D^H as a transform, the singular value X_k of R_hh is the channel energy contained in the kt h transform coefficient after transforming the LS estimate h ^ˆ . The dimension of the space of essentially time and band-limited signals leads us to the rank needed in the low-rank estimator. In [15] it is shown that this dimension is about 2 ^ T + 1, where p is the one-sided bandwidth and T is the time interval of the signal. Accordingly, the magnitude of the singular values of R_hh should drop rapidly after about L+1 large values, where L is the length of the cyclic prefix (2 ^ = 1 = T_s , T = LT_s and 2 /T + 1 = L + 1).

• IV.    Adaptive Modulation And Coding

Generally, AMC scheme is involved with a communication system in such a way that SNR or BER from receiving packets computed in receiver is feedback to transmitter by Channel Quality Indicator (CQI) to reconfigure itself for the other packet to be sent. The selection of the proper modulation and coding mode to be applied within the next transmission is created by the transmitter on the basis of the estimation of channel conditions i.e. instantaneous SNR for the next time interval of packets. In this selection of modulation and coding rate schemes, SNR thresholds are defined from individual performance of every scheme in the channel maintaining target BER of 0.01 or 0.001. The AMC performance depends upon the accurate channel estimation at the receiver and the authentic feedback path between the receiver and the transmitter on that the receiver accounts channel state information (CSI). To ensure that for AMC scheme to have a good performance, the delay between the standard channel estimation and the specific transmission with regards to the morel Doppler frequency of the channel ought to be as little as possible. Also, the transmitter needs to alert the receiver which modulation and coding rate scheme will be used during the transmission. Otherwise, that'll lead wrong demodulation and decoding of receiving packets which will compromise the performance.

• V.    Simulation Results

  In this paper, the OFDM parameters are focused on the WiMAX environment as shown in Table 1. Specifically the attention is going to be mainly focused on BER performance of Adaptive modulation schemes with Target-BER of 0.01 and 0.001. For AMC, channel state information is given by the LSE and MMSE channel estimators. Fig. 2 shows the magnitude and the frequency response of QPSK modulation scheme with FFT size 1024 for WiMAX. BER vs. SNR values have been compared in the Tables 2, 3 for BPSK, QPSK, 16QAM and 64QAM modulation schemes for different FFT sizes i.e. 256, 1024 and 2048. LSE and MMSE channel

estimators response to the specific channel response indicates in Figs. 3, 4 and 5.

Table 1: Parameter Definition.

Parameters	Values
Number of sub channels (N)	1024
Number of pilots (p=N/8)	128
Number of data subcarriers (N-P)	768
Guard interval length (GI=N/4)	256
Pilot position interval	8
Channel length	16
Channel	AWGN, Rayleigh
Digital Modulations	BPSK,QPSK, 8PSK, 16QAM, 64QAM, 256QAM

Table 2: BER vs. SNR for LSE channel estimator.

SNR db	BPSK FFT=256	BPSK 1024	BPSK 2048	QPSK 256	QPSK 1024	QPSK 2048
0	0.5213	0.5000	0.4063	0.5000	0.4297	0.4609
5	0.5156	0.4375	0.4063	0.5781	0.4688	0.4219
10	0.4063	0.4531	0.4688	0.3984	0.5234	0.5000
15	0.4688	0.4228	0.3750	0.3828	0.4688	0.4219
20	0.4844	0.5156	0.4531	0.4844	0.4531	0.4766
25	0.5938	0.5781	0.5000	0.4844	0.4922	0.4922
30	0.4531	0.5000	0.3750	0.4844	0.4766	0.4804

Table 3: BER vs. SNR for LSE channel estimator.

SNR db	16QAM FFT=256	16QAM 1024	64QAM 256	64QAM 1024	64QAM 2048
0	0.5313	0.5430	0.4922	0.5156	0.4922
5	0.4883	0.4766	0.4818	0.5026	0.4695
10	0.4805	0.5156	0.4974	0.4657	0.4922
15	0.4492	0.4453	0.4714	0.4635	0.4714
20	0.5078	0.4961	0.4844	0.5078	0.5651
25	0.5273	0.5391	0.5339	0.4896	0.4948
30	0.4648	0.4648	0.4896	0.5078	0.4661

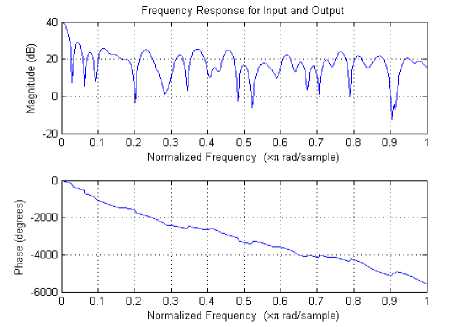
Fig. 2. Magnitude and Phase response for LSE channel estimator with FFT size 1024.

Fig. 3. Actual channel response.

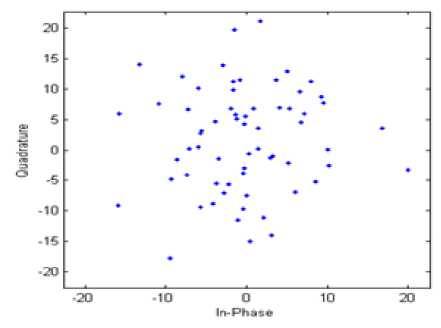
Fig. 4. Channel response by LSE channel estimator.

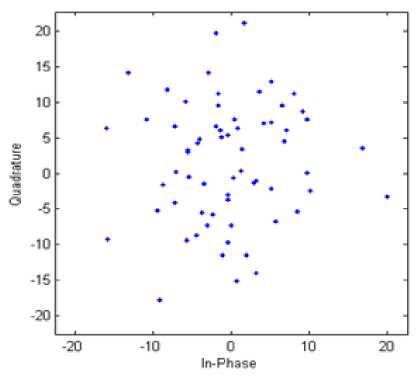
Fig. 5. Channel response by MMSE channel estimator.

The Target BER technique employed for AMC scheme is performed keeping in mind the error rate under a target limit say 0.01 or 0.001, maintaining a fixed level quality level of service with regards to error probability. Table 4 shows the SNR threshold to alter different modulation and coding rate based on SNR for target BER of 0.01. The Target BER technique operation is shown in Fig. 9 and the system keeps dealing with the lowest modulation and coding scheme, namely QPSK modulation with coding rate 1/2, until the signal-to-noise ratio allows to respect the error rate constraint, then the system switches on higher modulation transmission schemes to yield a much better spectral efficiency while maintaining our desired BER target. In Fig. 10, the throughput characteristics as a function of SNR for target BER of 0.01 is shown. If input data streams are transmitted using 64QAM with a coding rate of 3/4, the throughput is going to be maximized but there will be lower BER performance. So by compromising slightly the throughput performance, the modulation and coding rate schemes are changed to keep the error rate below our desired BER level.

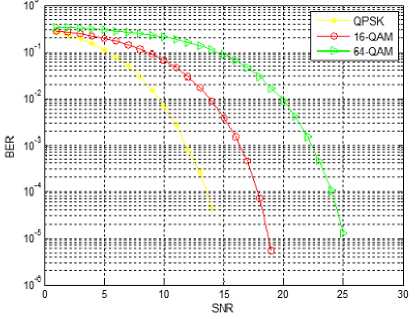
Fig. 6. BER performance without channel coding.

Table 4: Switching thresholds for AMC system.

MCS schemes	SNR thresholds(dB) Target-BER=0.01	SNR thresholds(dB) Target-BER=0.001
1/2 QPSK	< 8	< 10
3/4 QPSK	8 - 10	10 - 11
1/2 QAM16	10 - 12	11 - 13
3/4 QAM16	12 - 16	13 - 18
1/2 QAM64	16 - 18	18 - 20
3/4 QAM64	> 18	> 20

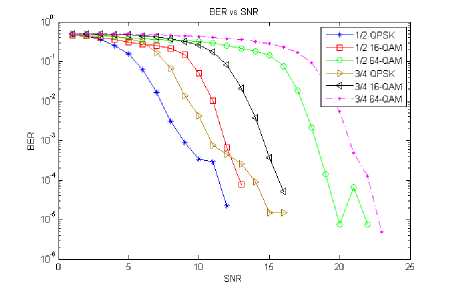
Fig. 7. BER performance of AMC system with convolutional channel coding.

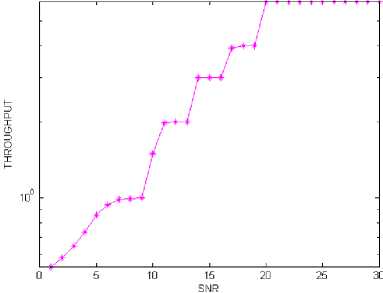
Fig. 10. Throughput of AMC system for Target-BER 0.01.

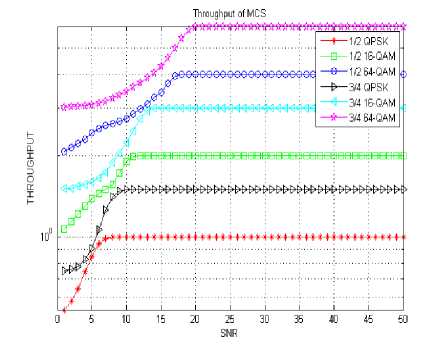
Fig. 8. Throughput performance of different MCS schemes.

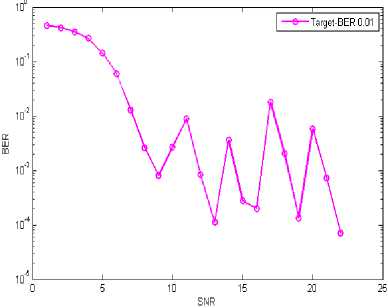
Fig. 9. BER performance of AMC system under Target-BER 0.01.

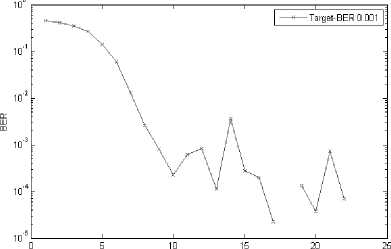
Fig. 11. BER performance of AMC system under Target-BER 0.001.

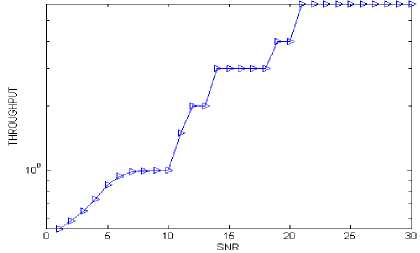
Fig. 12. Throughput performance of AMC system under Target-BER 0.001

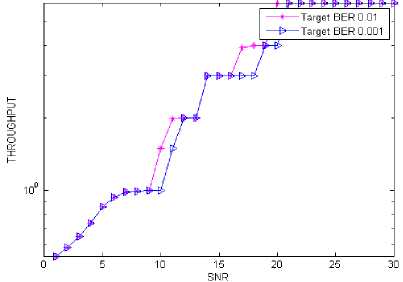
Fig. 13. Throughput comparison of Target-BER 0.001 and BER 0.01.

Figs. 14, 15 and 16 show the BER performance for Rayleigh fading channel [9] and Rician fading channels [10] for BPSK, 16QAM modulation scheme respectively with 1024 IFFT/FFT size. It can be concluded that, without channel estimation the BER has constant performance for all modulation schemes in both the channels. So, without channel estimation, the selection of the proper modulation scheme is difficult based on channel conditions. As modulation size increases, the BER value also increases at a given SNR value, which is a tradeoff. The BER value decreases, as SNR increases, but increasing SNR is a tradeoff in low power systems.

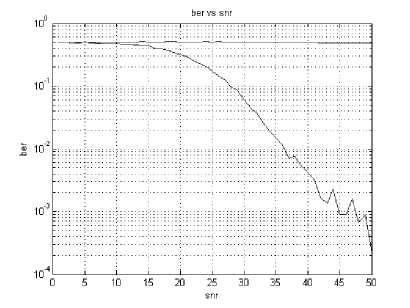
Fig. 14. Rayleigh fading channel performance for BPSK modulation scheme.

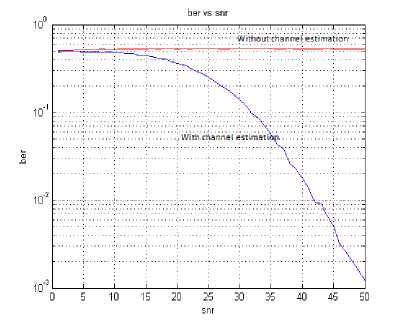
Fig. 15. Rayleigh fading channel performance for 16QAM modulation scheme.

BER Vs. SNR characteristics are presented in Figs. 17, 18, 19, 20 and 21 for different FFT lengths such as 128, 256, 512, 1024 and 2048 respectively. It can be observed that LS and LMMSE algorithms performed equally at higher SNRs especially more than 20 dB, however Lr-LMMSE performed well by giving low BER. At lower SNRs, LS algorithm performed well with low BER than remaining algorithms at large FFT length. Bit error rate is reduced gradually as FFT length increased at higher SNRs. Hence, high FFT length systems provide higher data throughput with error free transmission. LMMSE algorithm provided equal performance for all FFT lengths.

bervs snr

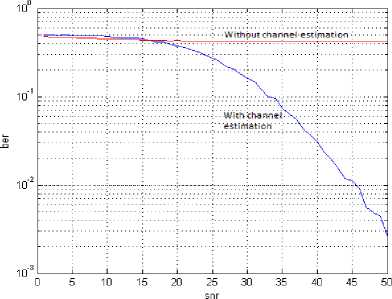
Fig. 16. Rician fading channel performance for 16QAM modulation scheme.

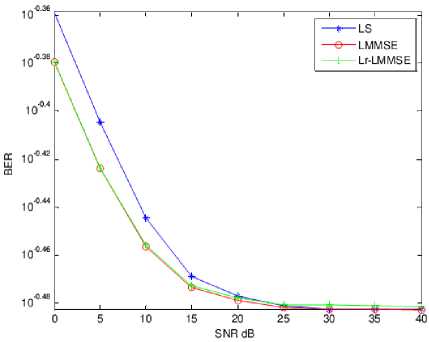
Fig. 19. BER Vs. SNR characteristics for FFT length 512.

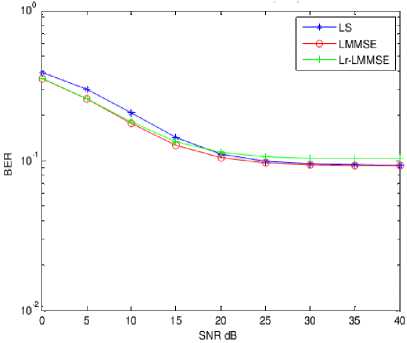
Fig. 17. BER Vs. SNR characteristics for FFT length 128.

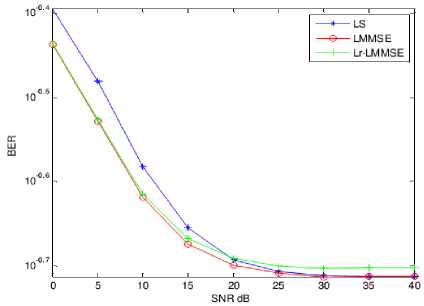
Fig. 18. BER Vs. SNR characteristics for FFT length 256.

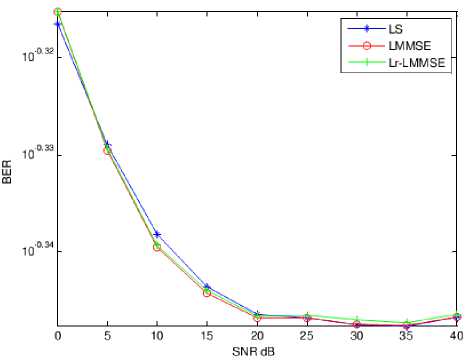
Fig. 20. BER Vs. SNR characteristics for FFT length 1024.

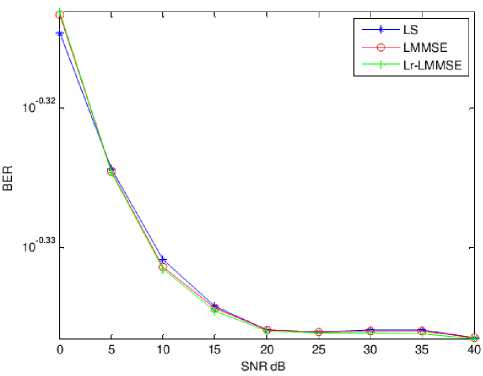
Fig. 21. BER Vs. SNR characteristics for FFT length 2048.

MSE Vs. SNR characteristics are plotted as shown in Figs. 22 and 23 for BPSK and 16QAM modulations respectively. It can be observed that LMMSE algorithm showed a better BER performance for 16QAM than BPSK modulation. LMMSE algorithm is applicable for higher modulation schemes and for higher SNRs.

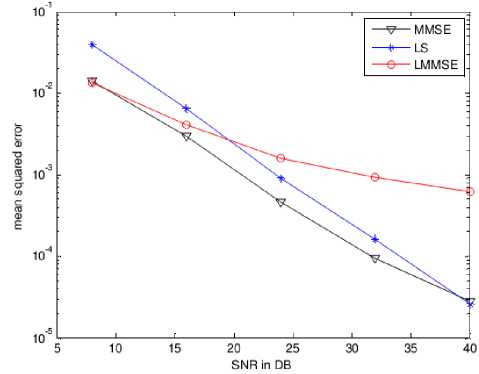
Fig. 22. MSE Vs. SNR characteristics for BPSK modulation.

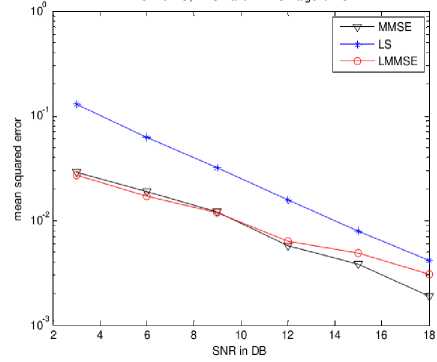
Fig. 23. MSE Vs. SNR characteristics for 16QAM modulation.

• VI.    Conclusions

This paper investigated the performance of OFDM systems with AMC in terms of BER, SNR, MSE and throughput. The code-rate of each subcarrier is adapted to subchannel state to maximize data rate and to satisfy average BER. The results concluded that higher modulation schemes give higher data rate with higher BER value. Lower modulation level schemes give a better BER performance with poor throughput performance.    Results    brought    a trade-off among the modulation level, BER, MSE, FFT length, algorithm selection and throughput. Target BER has been considered to compromise the BER vs. SNR values. Hence, care has to be taken while choosing a particular modulation scheme and channel estimation algorithm.