Adaptive Signal Processing for Improvement of Convergence Characteristics of FIR Filter

Finite impulse response (FIR) with Adaptive filtering techniques employs extensive applications in signal processing. The use of Multi-Rate (MR) structures for adaptive filtering was the main trend in the past as it provided the means of successfully overcoming the two major problems encountered in adaptive filtering applications.

It was already known in the late 1970s that the echo path in communication channels often consists of flat delays and dispersive regions. Multiple hybrid transformers in the channel cause multiple echoes. A typical example of a large flat-delay can be found in the satellite-linked communication channel. Coders and decoders (CODECs) and asynchronous transfer mode (ATM) networks, which are becoming more and more common these days, also introduce flat-delays by coding/decoding and cell handling. To model such an echo path, sparse-tap adaptive FIR filters have been known to be effective since the early 1980s. They have a smaller number of taps with coefficients than is required to span the entire impulse response. They essentially have higher potential in reduction of computations than recently developed algorithms [1, 4] that update a portion of coefficients corresponding to dispersive regions. Sparse-tap adaptive filters have a limited number of coefficients that are allocated to dispersive regions with a significant response. As the positions of flat-delay regions and dispersive regions are usually unknown a priori and different from a transmission channel to another, coefficients must be located adaptively within dispersive regions. Sparse-tap adaptive FIR filters can be divided into two groups: one realized as cascade connection of short-tap adaptive FIR filters and the other realized as a floating-tap adaptive FIR filter. The first group needs an auxiliary filter to determine the positions of the dispersive regions. After convergence of the auxiliary filter, the location information of the dispersive regions is transferred to a number of short adaptive FIR filters. Based on this information, each short filter is located along the tapped delay line such that it covers one of the dispersive regions. Two realizations of the auxiliary filter are known: one as a full-tap adaptive FIR filter and the other as an adaptive delay filter. When a full-tap adaptive FIR filter is used [5], the initial convergence speed is slow as it has a large number of taps to cover the whole impulse response. The auxiliary filter is operated at a reduced sampling rate. Although its computation is reduced thanks to sub sampling, there is no difference in terms of the convergence speed. Reduction is effective on the number of samples before convergence and not on the time needed to converge. For the case with an adaptive delay filter, the input signal is required to be sufficiently white for correct operation. This requirement is satisfied in some applications, and a better solution is desirable for other applications. Floating-tap adaptive FIR filters detect the dispersive regions by themselves, thus requiring no auxiliary filter. However, adaptive delay filters [6, 7] are not effective for a colored input signal such as speech, as pointed out earlier. The detection-guided NLMS algorithm [8] does not suffer from this problem. However, it is not suitable for unknown channels with a time-varying structure [8].

The use of Multi-Rate (MR) structures for adaptive filtering is the main current trend as it provides the means of successfully overcoming the two major problems encountered in adaptive filtering applications.

The first is related to the computational complexity; the second to the need for high convergence speed and good tracking performance. The MR Structures generally offer a reduction in the complexity, compared to a fullband configuration, owing to the fact that they adapt at a reduced data rate, a number of coefficients that is not significantly larger from the length L S of the system under modeling as shown in figure 1. The increase in the convergence speed they offer owes to the fact that in the sub-band domain the signals exhibit lower correlation levels, which means that the autocorrelation matrices of the input tap vectors of the adaptive algorithms have lower Eigen value spread. A classification of the MR structures can be made based on the way the system's input and output signals are analyzed. One approach is to use the same FB to analyze both as for example is proposed in [9, 10]. This is maybe the most popular approach. A second one is to use different networks for the analysis of these signals. The structure proposed in [11] is an example. It employed a MD Cosine Modulated (CM) FB of Near-Perfect Reconstruction (NPR) type to analyze the output signal of the system under modeling. Cross-products between adjacent analysis filters and their self-products were used to analyze the input signal of the system. The dual of this structure was recently presented. It was derived in a different way and employed products between adjacent analysis and synthesis filters of a CM FB, which was used to analyze the output signal of the system under modeling. This choice for the analysis network resulted in different solutions for the sub-band filter coefficients, for whose adaptation a new scheme was proposed which improved significantly the performance of the structure. The improvement in performance the new adaptation scheme offered, although substantial, came at no practical expense in the computational complexity.

Partial-update algorithms can be suitable for adaptive filtering applications requiring real-time and/or high density implementation. Typical examples in telecommunications are echo cancellation and equalization. In such applications there is a trade-off to be made in terms of the choice of the number of taps. The adaptive filter should be long enough to model the unknown system adequately. However, shorter filters normally converge more quickly and are computationally less demanding. The use of partial-update algorithms is a good approach to this trade-off in which sufficiently long filters can be employed but only a subset of the coefficients is adapted at each of iterations. Partial-update algorithms can be seen to exploit sparseness in two ways. When the unknown system's impulse response is sparse, such as in echo cancellation for network echo and in VoIP, many of the adaptive filter's taps can be approximated to zero.

Several algorithms were proposed to reduce the computational cost of the NLMS algorithm. Such algorithms include the periodic NLMS algorithm [l] and the partial update algorithms [12-14] where only a predetermined subset of the coefficients is updated at the iteration. Inevitably, the penalty incurred by using these algorithms is a lower performance, in terms of convergence speed, than the regular NLMS algorithm where all coefficients are updated. The decrease in convergence speed is proportional to the reduction in complexity and can be sometimes a major drawback in their implementation in the case of long impulse responses. The algorithm proposed here attempts to reduce the complexity of the NLMS algorithm while preserving a performance close to the regular NLMS algorithm. The algorithm is a member of the family of adaptive algorithms that updates a portion of their coefficients at the iteration, but it selects those coefficients adaptively to achieve the most reduction in the performance error. The proposed algorithm adds a maximum of 2 log2 (N) +2; (N being the adaptive filter length) comparison operations over the computational overhead of the algorithms in.

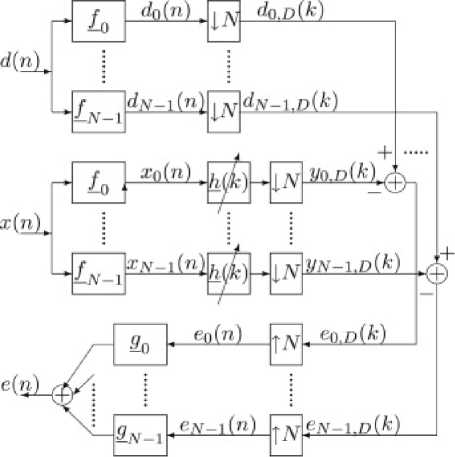
Figure1: Multi-rate Adaptive Filtering Scheme

Partial update NLMS algorithms have been developed to identify long FIR systems with reduced computational complexity compared to the standard NLMS algorithm [15, 19]. Best known partial update algorithms include periodical and sequential partial update LMS [15], M-Max NLMS [16], and selective partial update NLMS (SPUNLMS) [17]. Recently proposed Sparse Partialupdate NLMS (SPNLMS) [18] and coefficient and input combined selective partial-update NLMS (CIC-SPNLMS) [19] incorporate tap weight into partial selection criteria and provide very promising results for identifying long, sparse systems. These algorithms' performance have been analyzed and compared in the above referenced papers. However, there has not been a unified theoretical analysis on the convergence rates of the various algorithms. This paper discusses the general form of partial update algorithms' convergence for White Gaussian input and compares their performance in the sense of tap weight vector's mean deviation.

Adaptive filtering, as shown in figure 2, algorithms have been widely applied to solve many problems in digital communication systems [20-23]. The Least-Mean Square (LMS) algorithm has been widely used for adaptive filters, due to its simple structure and numerical sturdiness. On the other hand, the Normalized LMS (NLMS) algorithm is known that it gives better convergence characteristics than the LMS, because the NLMS uses a variable step-size parameter in which a fixed step-size parameter is divided by the input vector power at the iteration. However, a critical issue associated with both algorithms is the choice of the stepsize parameter that is the trade-off between the steadystate mis-adjustment and the speed of adaptation. Recent theories have thus presented the idea of variable step-size NLMS algorithm to remedy this issue. Also, many other adaptive algorithms based upon non-mean-square cost function can also be defined to improve the adaptation performance. For example, the use of the error to the power Four has investigated and the Least-Mean-Fourth (LMF) adaptive algorithm results.

The normalized least-mean-square (NLMS) algorithm ^{[24, 25]} is treated as one of the most popular adaptive algorithms in many applications. Since the NLMS algorithm requires O (2 L ) multiply accumulate (MAC) operations per sampling period, it is very desirable to reduce the computational workload of the processor. Partial update adaptive algorithms differ in the criteria used for selecting filter coefficients to update at each of the iteration. It is found that as the number of filter coefficients updated per iteration in a partial update adaptive filter is reduced, the computational complexity is also reduced but at the expense of some loss in performance. The aim of this paper is to propose improving the convergence characteristics of adaptive algorithm. It has been shown in [29] that the convergence performance of MMax-NLMS is dependent on the stepsize. Analysis of the mean-square deviation of MMax-NLMS is first presented and then a variable step-size in order to increase its rate of convergence is derived. The simulation results verify that the proposed variable stepsize MMax-NLMS (MMax-NLMSvss) algorithm achieves higher rate of convergence with lower computational complexity when compared to NLMS for white Gaussian noise (WGN).

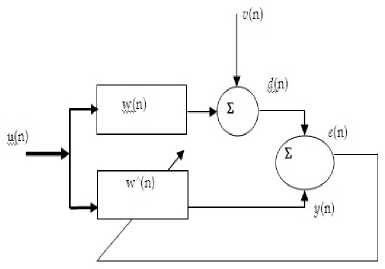
Figure2. Adaptive Filter Scheme

• II.    THE MMAX -NLMS ALGORITHM

The output at the nth iteration, v(n) = uT(n)h(n) where u(n) = [u(n),u(n-1), , u(n - L + 1)]T is the tap-input vector while the unknown impulse response h(n) = [ho (n), , hL_1(n)]T is of length L. An adaptive filter h(n) = [ho (n), , hL_1(n)]T which assumed [26] to be of equal length to the unknown system h(n), is used to estimate h(n) by adaptively minimizing a priori error signal e(n) using vˆ(n) defined by e ( n) = uT (n ) h (n) - v( n ) + g (n)                (1)

v( n ) = u T ( n ) h ( n _ 1)                             (2)

With g( n ) being the measurement noise.

In the MMax-NLMS algorithm ^[14], only those taps corresponding to the M largest magnitude tap-inputs are selected for updating at each iteration with 1 ≤ M ≤L . Defining the sub-selected tap-input vector,

u ( n ) = Q ( n ) u ( n )

where Q(n) = diag{q(n)} is an L x L tap selection matrix and Q(n) = [q0(n), . . . , qL-1(n)]T element qj(n) for j= 0, 1, . . . , L - 1 is given by,

9/ n ) =

”o

| u ( n — j )| e { MMa x imaof\u ( n )| } otherwise

Where

|^{u (n)}| = [| ^u(n)|,........ ,| ^{u( n _ L} + 1)| ] T

Defining . ² as the squared l 2 -norm, the MMax-NLMS tap-update equation is then

µ Q n u ne(n)

h (n ) =h (n _1)+   V-jH               (5)

u(n)| + C where C is regularization parameter.

Defining IL×L as the L x L identity matrix, it is noted that if Q(n) = IL×L, i.e., with M = L, the update equation in (5) is equivalent to the NLMS algorithm. Similar to the NLMS algorithm, the step-size μ in (5) controls the ability of MMax-NLMS to track the unknown system which is reflected by its rate of convergence. To select the M maxima of |u(n)|in (4), MMax-NLMS employs the SORTLINE algorithm [30] which requires 2log2L sorting operations per iteration. The computational complexity in terms of multiplications for MMax-NLMS is O(L+M) compared to O(2L) for NLMS. The performance of MMax-NLMS normally reduces with the number of filter coefficients updated per iteration. This tradeoff between complexity and convergence can be shown by first defining ^( n ), the normalized misalignment as

The Mean Square Deviation of MMax-NLMS can be obtained by first defining the system deviation as

£( n ) =

|| h (n)-h (n)|| II h ( n )l Г

б ( n ) = h ( n ) - h ( n )                             (7)

6 ( n - 1 ) = h ( n ) - h (n - 1)                  (8)

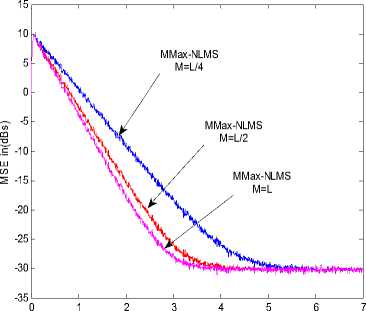
Fig.3 and Fig.4 shows the variation in convergence performance of MMax-NLMS with M for the case of L = 128 and μ = 0 . 1 using a white Gaussian noise (WGN) as input. For this illustrative example, WGN g( n ) is added to achieve a signal-to-noise ratio (SNR) of 15dB. It can be seen that the rate of convergence reduces with reducing M as expected.

Subtracting (8) from (7) and using (5), we obtain

0 ( n ) = о ( n - 1 ) +

д Q ( n ) u ( n ) e(n) u T ( n ) u ( n ) + C

III. MEAN SQUARE DEVIATION OF MMAX-NLMS

Defining ф { . } as the expectation operator and taking the mean square of (9), the MSD of MMax-NLMS can be expressed iteratively as

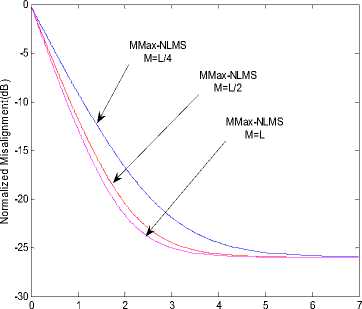
It has been shown in [29] that the convergence performance of MMax- NLMS is dependent on the stepsize μ when identifying a system. Since the aim of this paper is to reduce the degradation of convergence performance due to partial updating of the filter coefficients, from Fig.4 it is clear that the convergence performance decreases as M=L/4. Fig.5 shows the Normalized misalignment verses Time.

ф{| °(n)l 12} =ф{оТ(п)о( n)} =ф{| |°n-1)| 12}-ф^)}    (10)

Where фф(«)}

2ш T ( n ) o ( n - 1 ) e( n ) ^д\ u ( ⁿ )|| e^{2( n )}

u (n) ²

Time(s)

Figure 3: Convergence curves of MMax-NLMS for different M.

Assume that the effect of the regularization term C on the MSD is small. As can be seen from (10), in order to increase the rate of convergence for the MMax-NLMS algorithm, step-size ц is chosen such that ^ { Ф( Д ) } is maximized.

IV. THE PROPOSED MMAX-NLMS VSS ALGORITHM

Following the approach of [31], differentiating (11) with respect to μ and setting the result to zero [32] gives the variable step-size as

Time(s)

Figure 4: Normalized Misalignment curves for different M.

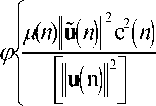
:ф>0 ( n - 1 ) ii( n ) || « ( n )||

12 T1

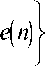
д( n)=/^ax X'

Q T ^{( n - 1 )} u ^{n )} | ^{u ( n )}| f] [ u ^{( n ) 0 ( n - 1 )}l u (n)² I u ( n )| 2 . n - 1 ) u ( n ) | u ( n ^"T ' u T ( n о ( n - 1 ) + c 2 M ( n )

Where 0 < μ max ≤ 1 limits the maximum of μ ( n ) and from [31].

М ( n )

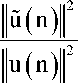
is the ratio between energies of the sub-selected tap-input vector u ( n ) and the complete tap-input vector u ( n ), while e g = ф { g ²( n ) } . Further numerator of д ( n ) can be simplified [32], by considering u ( n ) u T ( n ) = u ( n ) u T ( n )

e i ( n ) = [ Q ( n ) u ( n ) 1 ? ( n - ) as the error contribution due to the inactive filter coefficients such that the total error e ( n ) = e_a ( n ) + e_i ( n ). As explained in [29], for 0 . 5 L ≤ M < L , the degradation in M( n ) due to tap-selection is negligible. The reason for this is due to large enough value of M, the elements are small and hence the errors e i ( n ) are small, as is the general motivation for MMax tap-selection ^[28]. Approximating e a ( n ) ≈ e ( n ) in (15) gives

P n ) ® o P ( n - 1 ) + ( 1 - a ) u ( n ) [ u T ( n ) u ( n ) | e ( n )     (18)

6 T ( n - 1 ) u ( n )

I " ( n ilf.

- 1 u T ( n k n - 1 ) u n)

""—1

I u ⁿ )l ^{6 (} n - ¹ ) u ^{n )} I u n )|| u T ^{( n}M^{n 1 e} Mn

Using (16) and (18), the variable step-size is then given as

μ ( n ) can be further simplified by letting

P ( n ) = u ( n ) | u ^T ( n ) u ( n ) ] u ^T ( n ) k ( n - ) (13)

P ( n ) = u ( n ) [ u ^T ( n ) u ( n )^| u ^T ( n ) k ( n - ) (14)

From which it is then shown that

P ( n ) = P max

II P ( n )T

M ² ( n )| |p ( n )| |² + C

I ^{p n} )||^{2 =M} ( ⁿ ) ⁶ T ( ^n-1 ) ° ( n ) [l^u ( ^{n )} 12 ]^{u T} ( ⁿ к ( ^{n -1 )}

^P ( n )

= 6 ^T ( n - 1 ) u ( n )

^{u ( n )}

- 1

u ^T ( n ) к ( n - 1 )

Where C = M ² ( n ) e g . Since e g is unknown, it is shown that [32] by approximating C by a small constant, typically 0.0001 ^[31]. The computation of (16) and (18) each requires M additions. In order to reduce computation complexity even further, and because for M large enough values, the elements in Q ( n ) u ( n ) are small, approximating, ||P ( n )|| = ЦР* ( n )|| gives

Following the approach in [31], and defining 0 << a <  1 as the smoothing parameter, P ( n ) and

P ( n ) are estimated iteratively by

Pn)=opn-1)+(1-a)u(n)[uT(n)u(n)J ea(n)

Pn)=aP(n-1)+(1-a)u(n)[uT(n)u(n)J e(n)

where e ( n ) = uT ( n ) 6 ( n -1) in (16) while the error ea(n) due to active filter coefficients u(n) in ( 15) is given as ea (n) =uT (n) f( n-1) =uT (n)Гh( n)- /i(n-1)1

P ( n ) = P max

II^P ( n )| Г

^M 2 ( n )| IP ( n )| f + ^C

When Q ( n ) = I L×L , i.e., M = L , MMax-NLMS is equivalent to the NLMS algorithm and from (12), m ( n ) = 1 and||] P ( n )|| = ||P ( n )|| . As a consequence, the variable step-size μ ( n ) in (20) is consistent with that presented in [31] for M = L .

It is important to note that since u T ( n ) h ( n ) is unknown, e a ( n ) is to be approximated. Defining Q ( n ) = I _{L x L} - Q ( n ) as the tap-selection matrix which selects the inactive taps [32], we can express

V. SIMULATION RESULTS

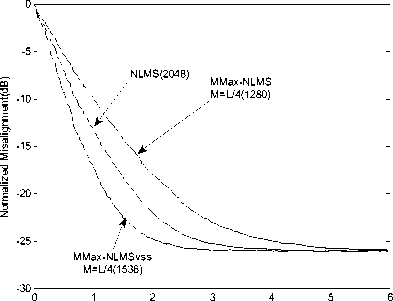
The performance of MMax-NLMS_vss in terms of the normalized misalignment is determined and defined in (6) using WGN input. With a sampling rate of 8 kHz and a reverberation time of 256 ms, the length of the impulse response is L = 1024. Similar to ^[31], C = 0.0001, α = 0 . 15are taken, WGN g ( n ) is added to v( n ) to achieve an SNR of 15dB.The value of μ max = 1 is taken for MMax-NLMS vss while step-size μ for the NLMS algorithm is adjusted so as to achieve the same steady-state performance for all simulations. Fig.6 shows the improvement in convergence performance of MMax-NLMS_vss over MMax-NLMS for the cases of M = L/4.

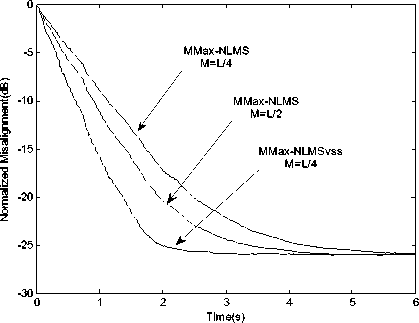
Figure 5: Improvement in convergence performance of MMax-NLMSvss over MMax-NLMS for different M.

Time(s)

Figure 6: Comparison curves of Convergence performance of MMax-NLMSvss with NLMS and MMax-NLMS.

The step-size of NLMS has been adjusted in order to achieve the same steady-state normalized misalignment. This corresponds to μ = 0 . 1. More importantly, the proposed MMax-NLMS vss algorithm outperforms NLMS even with lower complexity when M =256. This improvement in normalized misalignment of 7 dB (together with a reduction of 25% in terms of multiplications) over NLMS is due to variable step-size for MMax-NLMS vss . The MMax-NLMS vss achieves the same convergence performance as the NLMSvss ^[8] when M = L . In order to illustrate the benefits of the proposed algorithm, M = 256 taken for both MMax-NLMS and MMax-NLMS vss . This gives a 25% savings in multiplications per iteration for MMax-NLMS vss over NLMS. As can be seen, even with this computational savings, the proposed MMax-NLMS vss algorithm achieves an improvement of 1.5 dB in terms of normalized misalignment over NLMS.

VI. CONCLUSION

By analyzing the mean-square deviation of MMax-NLMS we can derive a partial update MMax-NLMS algorithm with a variable step-size during adaptation for improvement of convergence characteristics.

Computation of (18), computations of P ( n ) for (20) require M multiplications each. The computation of ||u ( n)|| and ||u ( n)|| for M ( n ) in (12) requires 2

multiplications and a division using recursive means.

Since the term u(n)|^uT (n)u(n)J e(n) is already computed in (18), no multiplications are now required for the update equation in (5).Hence including the

T computation of u (n) h (n -1) for e(n), MMax-

NLMSvss requires O ( L + 2 M ) multiplications per sample period compared to O (2 L ) for NLMS. The number of multiplications required for MMax-NLMSvss is thus less than NLMS when M < L/ 2.Although MMax-NLMSvss requires an additional 2 log2 L sorting operations per iteration using the SORTLINE algorithm ^[30], its complexity is still lower than NLMS. As with MMax-NLMS, we would expect the convergence performance for MMax-NLMSvss to degrade with reducing M . However, simulation results show that any such degradation is offset by the improvement in convergence rate due to μ ( n ).In terms of convergence performance, the proposed MMax-NLMS vss algorithm achieves approximately 3 dB improvement in normalized misalignment over NLMS for WGN input. More importantly, the proposed algorithm can achieve higher rate of convergence with lower computational complexity compared to NLMS.

ACKNOWLEDGMENT

We thank anonymous referees for their constructive comments. This research is supported by the Department of Electronics and Communication Engineering at School of Electronics, Vignan University, India with special focus on research. Special thanks to Mr. M. Ajay Kumar Research Scholar at IIT Guwahati, India for his technical support in writing this paper.