Адаптивная идентификация параметров систем отопления зданий

Введение. Системы отопления зданий являются сложными техническими устройствами, включающими в реальных условиях, как правило, разнотипные отопительные приборы с различными сроками эксплуатации и, возможно, с неодинаковыми схемами подключения к подводящим и обратным теплопроводам. При этом также следует иметь в виду, что структура и состав этих и так достаточно сложных систем довольно часто меняются, в частности, из-за пожеланий собственников квартир и по другим причинам. В связи с этим непосредственный анализ и отслеживание режимов работы таких систем является весьма трудной задачей. В некоторых случаях, например, при решении задачи синтеза управляющих алгоритмов удобно эту сложную систему представить эквивалентным отопительным прибором. Как это хорошо известно, основными теплотехническими параметрами отопительных приборов являются коэффициент теплопередачи k и площадь поверхности теплообмена F . Поэтому для решения задачи эквивалентной замены необходимо разработать процедуры оценки k и F по реальным данным. Данная задача рассматривается в настоящей работе.

Алгоритм оценки параметров первого варианта модели. Для оценки мощности системы отопления W _CO непосредственно необходимы не отдельные значения параметров k и F эквивалентного отопительного прибора, а их произведение ( kF )_СО , поэтому рассмотрим задачу оценки именно этого произведения. При этом будем использовать статическую модель системы отопления, представленную следующим уравнением:

W co = ( kF ) со ( t со - 1 в )/[1 + ( kF ) со / (2 cG со )], (1)

где t _СО – температура воды на входе системы ото-

пления, t _В – температура внутреннего воздуха, c –

удельная теплоемкость теплоносителя, G _СО – массовый расход воды через систему отопления.

Для упрощения последующих выкладок перепишем это уравнение в виде:

( kF ) со =------ " 'О _w .                 (2)

t co - 1 В - W?-

2 cG _CО

Нетрудно видеть, что это соотношение может быть записано так:

( kF ) co =

^cG CO ■ ⁽ t co t ОБр )

t co ⁺ t ОБР

^- t В

где t _ОБР – температура обратной воды.

Задачу адаптивной идентификации параметра ( kF )_СО сформулируем следующим образом. Пусть

известна оценка параметра ( kF )_{СО i} в i -й момент

времени, пусть, кроме того, для ( i + 1) -го момента времени получена новая информация с объекта управления ^- t СО( i + 1) , t ОБР( i + 1) , t В( i + 1) , ^G CO( i + 1) ■ Ставится вопрос: как, зная оценку параметра для i -го момента времени ( kF )_{СО i} , по новой информации с объекта управления найти новую улучшенную оценку этого же параметра - ( kF )_co ( i _{+ 1} ) ? При этом также понятно, что критерий идентификации должен иметь следующий вид:

I ( i + l)

= [( kF ) co i

^cG CO( i + 1) ■ ⁽ t СО( i + 1) t ОБР( i + 1) ) ] 2 (4) t СО( i + 1) ⁺ t ОБР( i + 1)

;,               t b( i + i)

Решая задачу, найдем, что

( kF ) со( i + 1) = ( kF ) со i - 2 h ■ [ " I,                 (5)

где под [ ■ ] понимаются квадратные скобки из (4)

со всем своим содержимым, а шаг h определяется из условия достижения минимума критерия (4) при отсутствии помех, т. е. h = 1/ 2 .

Если в формулу (5) подставить значение h = 1/2 и раскрыть скобки, то получим, что

^{( kF} ) СО( i + 1) =

c^G CO+1) ■ ⁽tСО(i+1)   t ОБР(i+1))

t CO( i + 1) ⁺ t ОБР( i + 1)

~              t В( i + 1)

, (6)

откуда видно, что алгоритм адаптации не имеет памяти, т. е. предыдущие значения параметра (kF )СО никак не влияют на его последующие зна- чения.

Точно такой же результат был получен и при использовании стандартного подхода [1], когда модель системы отопления представляется следующим образом:

W = ( kF )_co ■ ^f t ^{CO +} t ^ОБР - t _B ) .           (7)

СО      СО       2        В

Здесь критерий идентификации записывался так:

Ii+1 = [WCO(i+1)  (kF)COi Х tCO(i+1) + t ОБР(i+1)

Al ²

^- t В( i + 1)

J_

а последующие значения параметра ( kF )_СО ( i _{+ 1} )

определялись по соотношению

( kF ) со( i + 1) = ( kF ) со i + 2 h " Иx

I t CO( i + 1) ⁺ t ОБР( i + 1)

^Xl             "                t В( i + 1)

только содержимое квадратной скобки уже такое, какое оно в формуле (8), и совсем другое значение шага h :

h =

\ 2 .

^— t В( i + 1) I

2 1 t CO( i + 1) ⁺ t ОБР( i + 1)

первого порядка [2]. Однако возможно и применение подхода работы [1]: это за счет введения в формулу для h некоторого параметра ц, уменьшающего размер коррекции идентифицируемого параметра за один шаг, например, h вычислять по формуле h = —---------1----------v ’     (1 1)

| t СО( i + 1) ⁺ t ОБР( i + 1)             |

2Ц1             2              t В(i+1) I где должно быть, что ц> 1. В этом случае алгоритм адаптации уже не приводится к виду (6), у него появляется «память», как собственно это и записано в соотношениях (5) и (9). При этом заметим, что дать каких-либо общих рекомендаций по выбору параметра ц нельзя, требуется доводка, подгонка адаптивного алгоритма к конкретной статистической обстановке, в которой протекает исследуемый процесс.

Для апробации алгоритма (9)–(11) были использованы экспериментальные данные работы [3]. На рис. 1 приведены результаты оценки параметра ( kF ) _СО с помощью указанного адаптивного алгоритма: для ц= 1- кривая 1; для ц= 1,3 - кривая 2; для ц= 2 - кривая 3; для ц= 2,5 - кривая 4. Там же приведена оценка параметра ( kF )_СО , найденная неадаптивным методом наименьших квадратов, по формуле

N

^ W CO i ^Х A t СО i

( kF ) со = ^=1 ^ ------------.                 (12)

^ ^{( A} t СО i ⁾² i = 1

Это горизонтальная прямая 5, для нее ( kF )_СО = 12733,19 Вт/К.

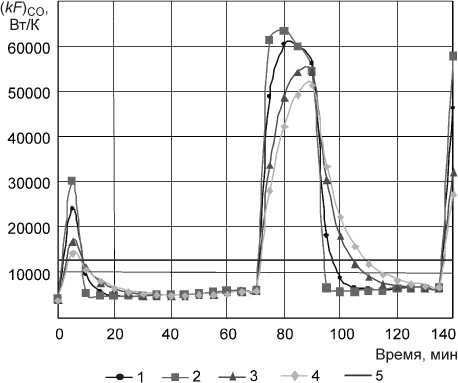
Рис. 1. Отслеживание параметра ( kF )_СО

Как видно из рис. 1, при ц = 1 для участков времени, для которых режим работы системы отопления можно отнести к условно стационарному, алгоритм дает, как нам представляется, достаточно правдоподобные оценки. Вместе с тем, для участков времени, когда режим работы становится отчетливо нестационарным, достоверность оценок параметра (kF)СО не является очевидной. По- видимому, здесь вся причина заключается в том, что используется не динамическая, а статическая модель системы отопления, так как понятно, что при резком изменении мощности системы отопления, в частности, при ее увеличении вследствие

* ,      toо + t обр инерционности параметр Atco =-----tВ не успевает изменяться в соответствии с соотношением (7), поэтому и получаются достаточно неточные, заметно завышенные оценки параметра (kF)СО . Таким образом, для общего случая необходима разработка динамической модели системы отопления. Разработанные же алгоритмы пригодны для оценки параметра (kF)СО по данным стационарного или же близкого к нему режимов работы системы отопления. С увеличением численного значения параметра ц оценки (kF)СО начи- нают меняться заметно медленнее, размеры скачков уменьшаются, все это, в общем-то, и следовало ожидать. Оценка параметра (kF)СО , найденная

Аргументы для этого следующие: во-первых, тепловой режим зданий имеет достаточно большую инерционность, постоянная времени T _В зданий составляет порядка 30 и более часов, во-вторых, все-таки нельзя считать, что температура наружного воздуха меняется слишком резко, обычно различают только дневную и ночную температуры наружного воздуха, т. е. считается, что t _Н меняется только два раза за сутки, в-третьих, температура теплоносителя в тепловой сети корректируется только один раз в сутки (как нам представляется, в основном из-за первых двух причин). Поэтому можно утверждать, что в реальных условиях температурный напор системы отопления

А        t cО ⁺ t ОБР ,

Atco =-------1В будет меняться достаточно медленно и, вследствие этого (kF)СО также будет изменяться медленно, что и позволит эффективно отработать это изменение.

Тем не менее, все-таки учтем, что коэффициент теплопередачи эквивалентного отопительного прибора (система отопления здания может быть представлена эквивалентным отопительным при-

бором) вообще-то зависит от температурного на-

M - t СО ⁺ t ОБР пора ^A t co =     2

—

t _В , в этом случае модель

системы отопления будет представляться следующим уравнением:

W co = ( mF ) co ( A t co ) n ⁺ 1 •

неадаптивным методом наименьших квадратов (прямая 5), также не учитывает инерционные свойства системы отопления и получается заметно отличной от того значения, которое следовало бы ожидать для данных стационарного режима. Отметим, однако, что причиной существенной неста-ционарности рассматриваемого процесса на отдельных его участках являются не столько реальные условия эксплуатации систем отопления, сколько желание автора работы [3] изучить особенности применения двухпозиционных регуляторов, экспериментальные данные получены именно для этих условий.

Алгоритм оценки параметров второго варианта модели. Следует заметить, что коэффициент теплопередачи k как отдельного отопительного прибора, так и, очевидно, и всей системы отопления зависит от температурного напора, который для всей системы отопления, как известно,

Применим к уравнению (13) следующее линеаризующее преобразование: сначала прологарифмируем обе его части, а затем введем нижеуказанные обозначения:

toW co ) = ln( mF )со + ( n + 1) ■ ln( A t со ); (14) y = ln( W _co); a = ln( mF )_co; b = ( n + 1); x = ln( A t _co).

В этом случае уравнение (13) запишется в виде y = a + bx , задача параметрической идентификации этого уравнения достаточно хорошо проработана, известны как неадаптивный, так и адаптивный алгоритмы идентификации [1]. В частности, адаптивный алгоритм представляется следующими соотношениями:

a i + 1 = a i + 2 h ■ [ ■ ];

b i + 1 = b i + ² h ■ [ ■ ] ■ x + 1 ;

[ ■ ] = y i + 1 ^— a i ^— b i x i + x ;

вычисляется

_ t со ⁺ t ОБР

СО       2

следующим

образом:

h =-----'

2(1 + x ^i)

.

— t В . Разработанный адаптивный

алгоритм идентификации комплексного параметра ( kF )_СО предназначен для отслеживания вообще-то любых изменений этого параметра, в том числе и в зависимости от температурного напора. Нет никаких оснований сомневаться в том, что, в частности, последняя задача будет успешно решаться.

Здесь также для уменьшения влияния помех следует ввести параметр ц в формулу (18), которая в этом случае запишется уже в следующем виде:

h =---1^,

2( ц + x i + ₁ ⁾

где также должно быть, что ц >  1.

Подчеркнем, однако, что адаптивный алгоритм (15)–(19) может оказаться недостаточно эффективным из-за малой вариабельности (разнообразия) экспериментальных данных для оценки двух параметров ( mF )_СО и n [1], повлиять на эту ситуацию нельзя, так как сбор данных ведется в условиях нормальной эксплуатации системы отопления. Когда же оценивается только один параметр ( kF )_СО , то проблема малой вариабельности экспериментальных данных уже не является критической.

На рис. 2 и 3 приведены результаты применения алгоритма (15)–(19) для оценки параметров (mF)СО и n соответственно при ц = 1. При этом заметим, что оценки параметров (mF )СО и n , найденные при ц = 1,3; 2; 2,5, оказались практически теми же, что и при ц = 1. Произошло это, по всей видимости, из-за того, что в формуле (19) 2 _ xi+1 >> ц , поэтому для использования привычного диапазона изменения параметра ц формулу для h модифицировали и стали использовать в следующем виде:

2 ц (1 + x 2 _{+ 1})'

На рис. 4 и 5 приведены результаты применения алгоритма уже с h , вычисляемым по формуле (20), для ц = 1 и для ц = 2 . Как видно из рис.

4 и 5, фильтрующие свойства алгоритма при ц> 1

начинают проявляться достаточно заметно.

Вместе с тем, следует, однако, признать, что оценки параметра n (ее отрицательные значения) не кажутся правдоподобными. Тем не менее, если учесть, что (kF)СО = (mF)СО • (AtСО)n и подставить в эту формулу при ц = 1 данные из рис. 4 и 5 и AtСО , соответствующие данному моменту времени, то полученное значение будет практически совпадать с тем, что приведено на рис.1, когда параметр (kF )СО оценивался непосредственно по экспериментальным данным, а не через оценки (mF )СО и показател n . Все это изображено на рис. 6, на котором приведены результаты оценки параметра (kF )СО : кривая 1 – когда (kF )СО оценивался непосредственно; кривая 2 – когда

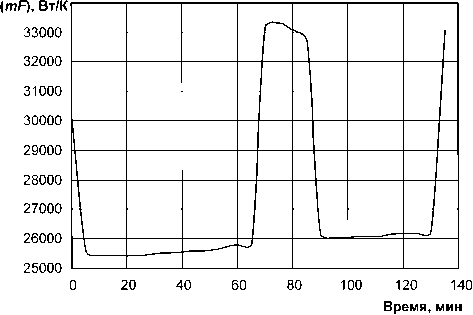
Рис. 2. Отслеживание параметра ( mF )_СО

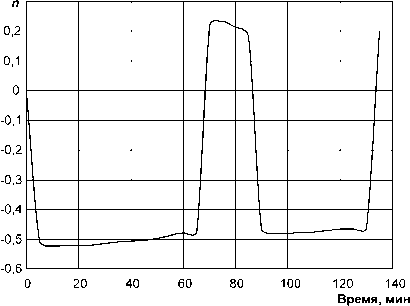
Рис. 3. Отслеживание параметра n

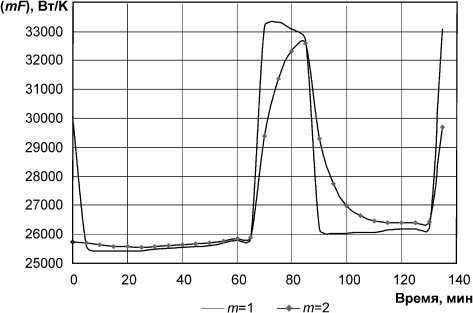
Рис. 4. Отслеживание параметра ( mF )_СО

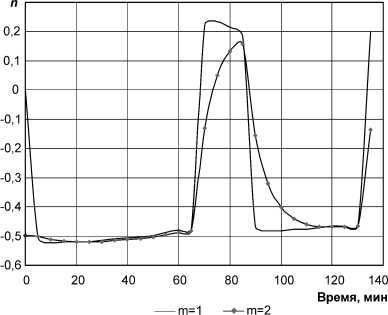
Рис. 5. Отслеживание параметра n

при h =

2 ц (1 + Х 2 + 1 )

при h =-------—

2 ц (1 + х^

( kF )_СО  вычислялся по оценкам параметров

( mF )_СО и n .

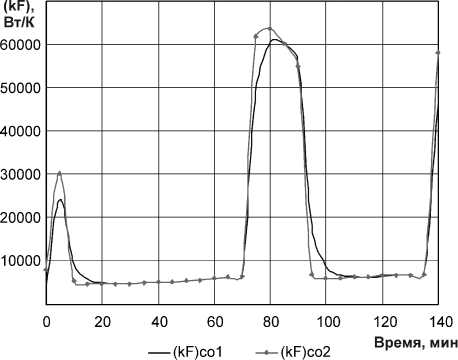
Рис. 6. Оценки параметра ( kF )_СО

Поэтому, как мы и ожидали, нет большой необходимости в определении отдельных показателей ( mF )_СО и n .

Относительно того, что оценки параметра n не кажутся правдоподобными можно отметить следующее. Возможно, что таким образом проявляется то, что используются только статические модели системы отопления. Возможно также и то, что задача оценки не решается однозначно либо кратность «прогонки» экспериментальных данных через адаптивный алгоритм не достаточна. Очевидно, необходимо дополнительное исследование свойств алгоритма совместной оценки параметра (mF)СО и показателя n .

Выводы. Разработаны и апробированы два варианта алгоритмов оценки теплотехнических характеристик систем отопления, представляемых эквивалентным отопительным прибором, по экспериментальным данным. Установлено, что алгоритмы обладают заметными фильтрующими свойствами и могут быть использованы в составе алгоритмического обеспечения систем управления процессом теплоснабжения.