Адаптивная эталонная модель в системе управления беспилотного летательного аппарата

Структура адаптивной системы управления беспилот ного летательного аппарата. Рассмотрим систему автономного адаптивного управления (рис. 1), использующую в своей структуре нечеткий блок-идентификатор (БИ), ос- новной контур, состоящий из объекта управления (ОУ) – беспилотного летательного аппарата (БПЛА) и регулятора; самонастраивающуюся нечеткую эталонную модель системы (ЭМ); блок адаптации и наблюдатель ρˆ .

Полученная система выполняет следующие задачи:

– обеспечение эталонных динамических характеристик системы управления БПЛА для всех режимов полета;

– идентификацию параметров БПЛА в полете для настройки ЭМ, при этом используется устройство с памятью;

– обеспечение компенсации внешних конечномерных возмущений, для чего используется наблюдатель, формирующий оценку возмущения ρ ˆ ;

– реализации алгоритма адаптации: блок адаптации реагирует на ошибку e = y - y _Э между сигналами с выхода ОУ и ЭМ, а также осуществляет адаптивную подстройку к изменяющимся внешним воздействиям ρ ( t ).

Далее рассмотрим более подробно нечеткий блок-идентификатор (БИ).

Нечеткий блок-индентификатор. С целью оценки параметров ЛА предполагается использовать адаптивную

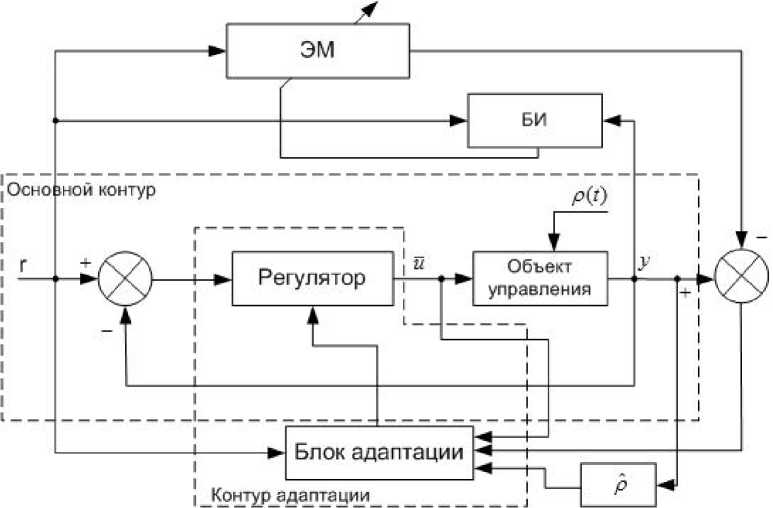
Рис. 1. Структурная схема адаптивной системы автономного управления

модель с нечетким выводом, со структурой, приведенной на рис. 2.

Данный блок-идентификатор позволяет устранить следующие недостатки, присущие нечетким системам:

– дает возможностьдополнятьисходный набор правил, описывающий состояния системы управления, который формируется человеком и вследствие чего может иметьнеполный набор правил, противоречивые или идентичные правила;

– оптимизировать параметры модели управления, которые изначально задаются экспертом субъективно, что снижает качество идентификации. Целенаправленное изменение параметров нечеткой модели, таких как количество, форма, относительное размещение соответствующих функций принадлежности вдольбазовых осей оказывают существенное влияние на характер идентификации.

Блок-идентификатор состоит из базы знаний, которая представляет собой совокупность информации о базе нечетких правил и множестве лингвистических перемен-ныхс соответствующими функциями принадлежности.

Работа по формированию базы знаний происходит в два этапа:

–на первом этапе база знаний формируется на основе обучающей выборки, которая состоитиз параметров наблюдений с соответствующими принадлежностями классам наблюдений и доступной априорной информации об объекте у эксперта;

– на втором этапе происходит параметрическая оптимизация к дискретному изменению динамики объекта управления.

Далее блок-идентификатор формирует оптимальную аппроксимацию для входных обучающих данных X ( ϑ , M, δ ), где ϑ ,M, δ- уголтангажа,числоМахаиугол отклонения руля высоты соответственно.

После обучения блок-идентификатор реализует следующее уравнение [1]:

n y ( k ) = F (M( k ), C [ ϑ ( k ),M( k ), δ ( k )]), (1) где n_y - нормальная перегрузка; C - аэродинамический коэффициент подъемной силы.

Самонастраивающаяся нечеткая эталонная модель. Предполагается использование такой ЭМ, которая при работе линейного регулятора, обеспечивающего устой-чивостьна всех режимах полета, улучшала бы качество системы управления БПЛА, используя свои адаптивные свойства совместно с блок-идентификатором (БИ).

Для этого БИ содержит следующую информацию о параметрах БПЛА:

• 1)    динамические параметры:

  – максимально допустимое перерегулирование [2]:

_{Mp max = e} -π ( ι /1 -ι ²) _{× 100%;             (2)}

– экстремальные значения собственной частоты (с затуханием и без затухания) ω _{max d} и ω _max0 ;

• 2)    текущие значения параметров, измеряемые датчиками ДПЛА:

• – текущие углы крена γ , тангажа σ , курса ψ ;

  – текущая скорость M ( t );

• 3)    константы максимально допустимых значений:

• –    максимально допустимые (если такие имеются согласно ТЗ) углы крена γ , тангажа σ , курса ψ ;

• –    максимально допустимая скорость M _max ( t );

• –    максимально допустимые перегрузки n_x , n_y , n_z ;

• –    максимальные углы отклонения рулей;

• 4)    идентифицируемые параметры:

• –    результат идентификации параметров БПЛА.

Далее будет рассмотрено моделирование блока-идентификатора системы управления БПЛА в ПП Simulink и Fuzzy Logic Toolbox [3–6].

Исследование работы нечеткого блока-идентифика тора. Блок-идентификатор (БИ) проектировался на основе систем нечеткого вывода в Fuzzy Logic Toolbox [6].

В качестве входных параметров системы нечеткого вывода будем рассматривать следующие нечеткие переменные: угол тангажа ϑ , число Маха M , отклонение руля высоты δ , ав качестве выходного параметра – оценка перегрузки ДПЛА n ˆ _y . БИ моделирует зависимость (рис. 3) в соответствии с системой нечеткого вывода типа Момдами:

n ˆ y ( k ) = K z M ²( k )sgn( ϑ )[ a ˆ n ϑ ( k ) 3 ₊

+ b ˆ n ϑ ( k )² + c ˆ n (2 - M ( k )/3) ϑ ( k )] + d ˆ n δ ( k ),      (3)

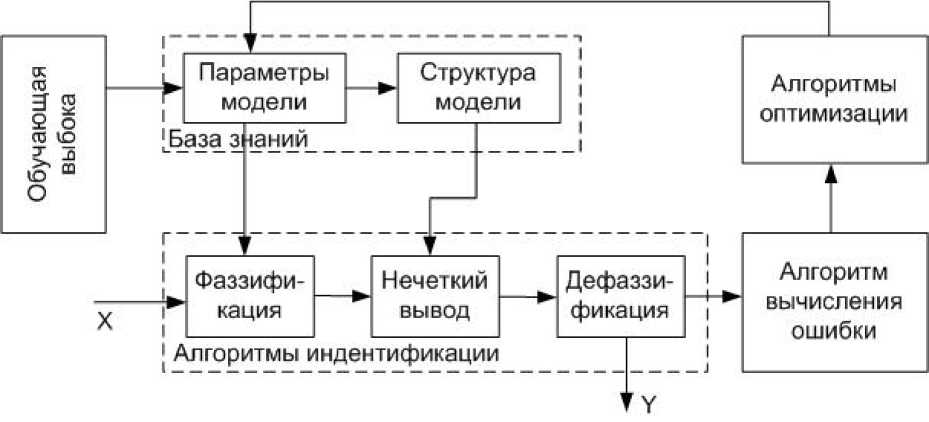
Рис. 2. Структура нечеткой модели блока идентификации

где ϑ ( k ),M( k ), δ ( k ) ∞ и n ˆ _y ( k )–значения входных и выходных переменных объекта управления в дискретные моменты времени k >  0 , a ˆ _n , b_n , c ˆ _n , d_n - аэродинамические коэффициенты ДПЛА.

Оценка перегрузки ДПЛА

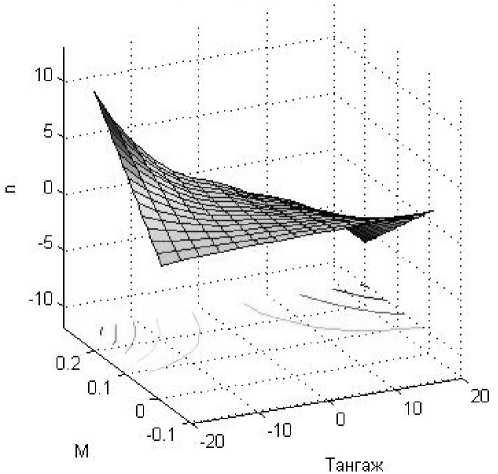
Рис. 4. Искомая зависимость: оценка перегрузки n_y ДПЛА

Областьизменения входных параметров следующая: ϑ ∈ [-20; 20], M ∈ [0;0,2], δ ∈ [-20; 20].

Адекватностьполученной нечеткой модели проверялась по следующему критерию: найти такой вектор ( P , W ), чтобы[3]:

Membership function plots

-5            0            5

input variable "tang!"

0.5 - plot points:

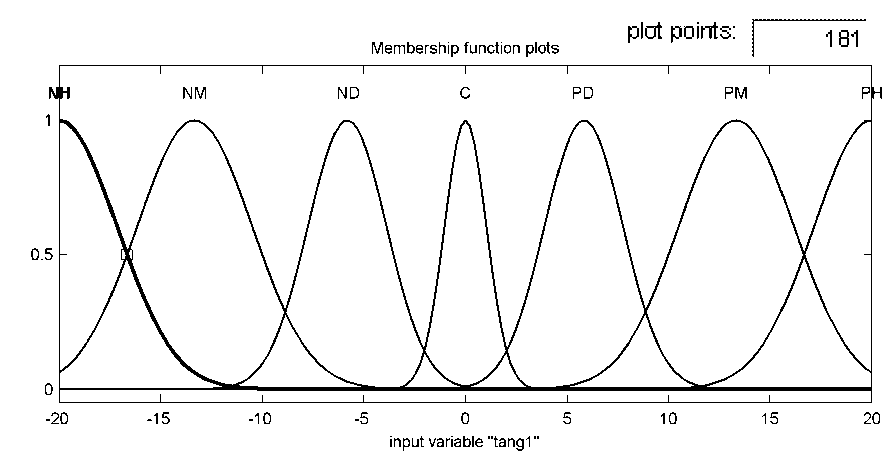
Рис. 5. Функции принадлежности переменной ϑ в Membership Function Editor

RMSE=1 ∑(yr-F(P,W,Xr))2 →min, (4) N r=1,N где P - вектор параметров функций принадлежности термов входных и выходной переменных; W ∈[0; 1] - вектор весовых коэффициентов правил базы знаний; N - пары из обучающей выборки; Xr - входные переменные; yr - выход системы; F (P,W, Xr) – результат вывода по нечеткой базе знаний Мамдани с параметрами (P,W)призначениивходов Xr .

Входы и выход нечеткой модели будем рассматривать как лингвистические переменные. Значение для переменной «угол тангажа» определяются из следующего терм-множества: {PH, PM, PD, C, ND, NM, BH} или {положительно высокий, положительно средний, положительно низкий, не меняется, отрицательно низкий, отрицательно средний, отрицательно высокий} для ϑ . Термы представим нечеткими множествами с гауссовыми функциями принадлежности. Возможный вид функции принадлежности для входной лингвистической переменной «угол тангажа» приведен на рис. 4.

Далее создадим лингвистическое описание параметров нечеткой модели БИ с помощью базы нечетких правил типа

M: если X есть А и...и X есть A, i1i1... mim, то Y1 есть Di1 и...и   Yn есть Din.    (5)

Для составления и отладки базы нечетких правил использовались обучающие данные перегрузки n_y (рис. 5).

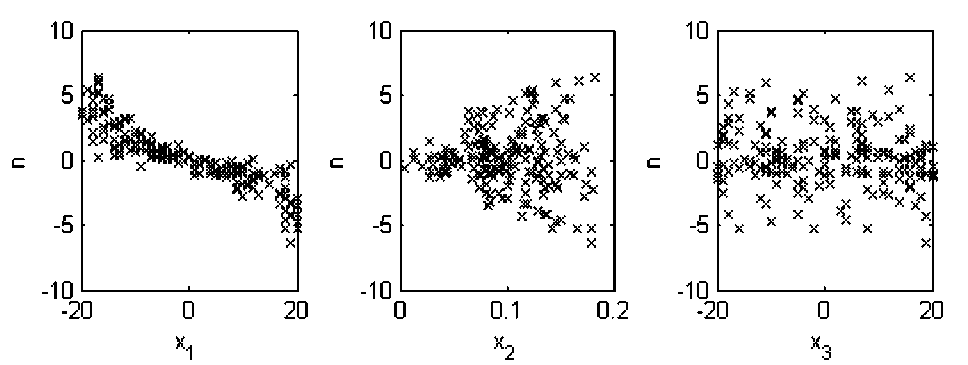
Рис. 6. Обучающая выборка для идентификации зависимости оценки перегрузки n_y от угла тангажа ϑ= x ₁ , числа Маха M = x ₂ , отклонения руля высоты δ= x ₃

После обучения нечеткой базы знаний была получе- на зависимость идентифицируемой перегрузки nˆ от входных переменных ϑ , M , δ (рис. 6).

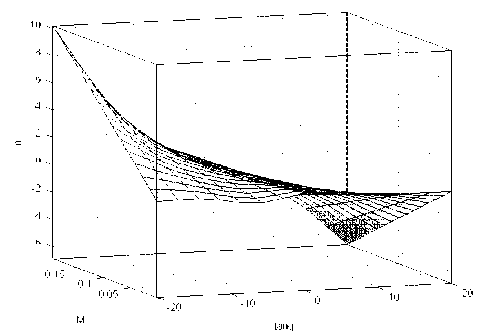
Рис. 6. Идентифицируемая перегрузка ny , tang – тангаж рекомендуется прекращать обучение при возрастании ошибки на тестовой выборке.

п.09

0.01 ----------------------1----------------------1----------------------1----------------------1----------------------1----------------------

0          50         100         150         200         250         300

Итерации алгоритма обучения

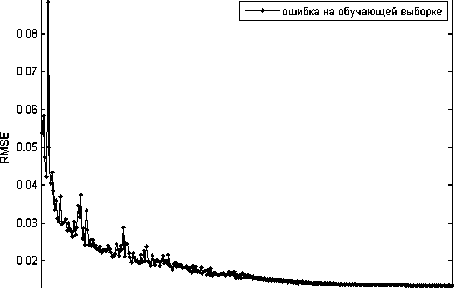
Рис. 8. Зависимостьошибок нечеткого моделирования от количества итераций обучения на обучающей выборке

Более наглядное сравнение экспериментальных данных из тестовой выборки с результатами нечеткого моделирования показаны на рис. 7.

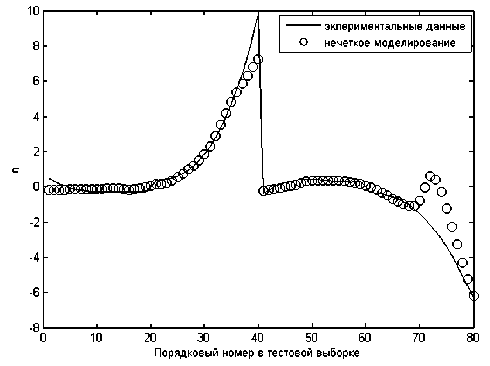
Рис. 7. Тестирование нечеткой модели БИ

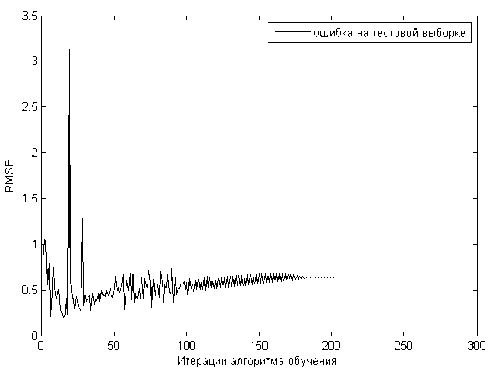
Рис. 9. Зависимостьошибок нечеткого моделирования от количества итераций обучения на тестовой выборке

Нечеткая модельописывает динамику эксперименталь- ных данных, однако в отдельных случаях имеются значительные расхождения в оценки перегрузки nˆy (см. рис. 7). Повысим точностьнечеткой модели в оценки перегрузки nˆy с помощью обучения нечеткой базы знаний.

Обучение нечеткой модели осуществим квазиньюто-новским методом [5] Бройдена–Флетчера–Голфарбда– Шэнно на протяжении 300 итераций.

Определим, как влияет длительность обучения на адек-ватностьнечеткой модели, для этого построим следующие зависимости (рис. 8, 9).

Значение невязки (6) с ростом количества итераций уменьшается, и после 200 итераций квадратичная ошибка моделирования на обучающей и 50 итераций на тестовой выборках равны 0,001 1 и 0,236 1 соответственно (см. рис. 8, 9). После этого ошибка на тестовой выборке начинает немного возрастать, и начиная примерно с 49 выборки проявляется эффект переобучения. Это объясняется тем, что вне точек обучения адекватностьпереобу-ченной модели низкая – результаты моделирования сильно отличаются от экспериментальных данных, поэтому

После обучения и настройки нечеткой базы знаний адекватностьмодели заметно улучшилась (рис. 10).

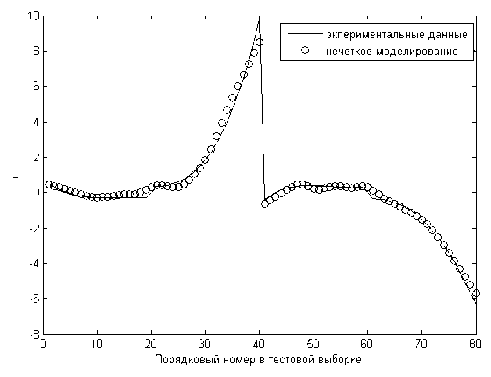
Рис. 10. Тестирование нечеткой модели БИ после настройки

Заключение. В результате исследования была показана целесообразностьприменения адаптивной эталонной модели с блоком-идентификатором на нечеткой логике, которая обеспечивает адаптацию эталонной модели к широким изменениям режимов полета БПЛА.