Адаптивная обучаемая модель обнаружения уязвимостей интерфейсов БТС на основе вероятностных автоматов

Предлагаемый в статье подход ориентирован на решение задач обнаружения моментов времени изменения состояния контролируемых ресурсов БТС, каковыми являются ресурсы: канал связи, процессор, память. При этом скорость и достоверность оценки ситуации может иметь решающее значение. Реализация таких задач в реальном времени не всегда возможна с помощью аналитического подхода, поскольку эти задачи характеризуются противоречивостью, нелинейностью, недифференцируемостью, многоэкстре-мальностью, сложной топологией области до- пустимых значений, высокой вычислительной сложностью оптимизируемых функций, высокой размерностью пространства поиска и т. п. В условиях дефицита априорной информации большая часть проблем анализа данных связана с исследованиями стохастических систем [1–2]. Одним из наиболее эффективных инструментов моделирования сложных стохастических систем является методология вероятностно-автоматного моделирования [3]. Вероятностные автоматы используются в таких областях, например, как: логическое управление, математическая лингвистика, теория формальных языков, моделирование поведения человека, при описании моделей информацион- ной защиты предприятия и др. Продуктивность указанной методологии обусловлена возможностью построения унифицированных моделей для широкого класса систем и использованием систем поддержки принятия решений при необходимости в точной оценке выбора различных альтернатив на основе вероятностных автоматов.

Настоящая работа посвящена применению модели обучаемых вероятностных автоматов для обнаружения уязвимостей объектов, к числу которых, например, относятся интеллектуальные системы управления беспилотными воздушными и наземными транспортными средствами, системы, обеспечивающие межмашинное взаимодействие с использованием технологии интернета вещей и др. Разнородность приложений и беспроводных коммуникаций в инфраструктуре умного города существенно усложняет обеспечение безопасности объектов [4]. Методы предупреждения атак для безопасной эксплуатации транспортных средств должны быть динамичными и реагировать на возможные угрозы. Упреждающий подход к угрозам должен быть ключевым требованием, которое должно быть выполнено. Однако поскольку невозможно предсказать все возможные угрозы для БТС, то важно, чтобы в результате атаки у пользователей было как можно меньше нарушений [5–7].

В настоящее время известны различные вероятностные автоматные модели. Причина разнообразия автоматных моделей объясняется широтой области их применения.

Постановка задачи

Целью работы является разработка адаптивной модели с использованием вероятностного оценивания состояний ресурсов БТС. Модель базируется на основе вероятностного автомата с адаптивной самонастройкой. На основе предлагаемой модели решается задача оценки состояний ресурсов с целью повышения достоверности результатов классификации информационных ситуаций. Обозначим

R = { Ri ,..., Rj,^, Rr} множество контролируемых ресурсов БТС. Определим контролируемые характеристики ресурсов, по которым будем оценивать их состояние (значения характеристик нормированы, определены в диапазоне [0;1]): Dj – загрузка j-го ресурса, Vj - скорость изменения Dj, где V = = ( D (tt)-D (^))/ At.

Указанные характеристики – векторные величины с компонентами элементов множеств R j .

S*o s',             ......... S*j

O Io /1 lj-i 1

Рисунок 1. Области различия состояний S t ресурса R j

Обозначим S^t_j – состояние i -го ресурса в момент времени t . При достаточно общей постановке задачи речь идет о контроле результатов наблюдений над состоянием ресурсов БТС. Значения состояний определены и нормированы в диапазоне [0;1]. Пусть состояния определены на интервалах [ I k ; I k _{+ 1} ] , где I k - порог для задания области определения состояния ресурса, к = = 0 , 1 ,..., j . На рисунке 1 приведен пример различия состояний S^t_j ресурса R_j на интервалах

S 0 е [ 0 ; I о ] , S t e ( 1 ₀ ; 1 1 ] ,..., S j е ( I ^] .

Без потери общности далее будем рассматривать три возможных состояния ресурса - S ₀ , S 1 , S 2 . Предположим, что область с номером «0» обозначает нормальное состояние ресурса, область с номером «1» – предкритическое состояние, а область с номером «2» – критическое состояние.

Основной задачей является адаптивная оценка значений вероятности состояний ресурсов БТС, сформированных для нормального поведения ресурса на временном интервале T и полученных значений в результате внешнего воздействия на интервале Т_внеш . Применение указанной модели позволит получить достоверные оценки гипотез появления состояний S i .

Метод обнаружения изменения состояния ресурсов БТС

Будем фиксировать изменения состояния S^t_j ресурса на временном интервале T_N в моменты времени { t ₀ , t 1 , .„, t j , .„ , t n } c использованием автоматной вероятностной модели. Каждому такту сопоставляется входной сигнал о состоянии ресурса – Х , выходной сигнал – Y и сигнал о внутреннем состоянии – S . Будем рассматривать автоматную модель Мура:

£ = ( S , X , Y , Ф , V , S h ) , (1) где S H e S - начальное состояние, S - множество значений вектора состояния, X – множество значений входного вектора, Y – множество значений выходного вектора, Φ – функция переходов, Ψ – функция выходов.

В этом случае элементы матриц переходов и выходов представляют собой соответствующие

Таблица 1. Пример начального распределения состояний вероятностного автомата

* ( s j ( t +1 ) )	Y ( t +1 )	Y ( t +1 )		Y j ( t +1 )		Y m ( t + 1 )
ф ( s j ( t ) , x ( t ) )	S o ( t + 1 )	S ( t +1 )		S j ( t +1 )		S m ( t + 1 )
S . ( t )	P 0	P 1		P j		P m

Таблица 2. Таблица переходов Ф ( S i j k ) вероятностного автомата

		S o ( t + 1 )	S 1 ( t +1 )		s , ( t +1 )		S m ( t + 1 )
x ( t )	S 0 ( t )	Г ,0,0	r ,0,1		r ,0, j		r i ,0, m
x ( t )	S 1 ( t )	Г ,1,0	ri -,1,1		r ,1, j		r i ,1, m
x ( t )	S j ( t )	r , j ,0	r ., i , j ,1		r . . i , j , j		r i , J , m
x ( t )	s. ( t )	r. „ r i , m ,0	r. . r i , m ,1		ri , m , j		r i , m , m

Таблица 3. Таблица выходов ^ ( Y i j ) вероятностного автомата Мура

	Y , ( t + 1 )	Yx ( t +1 )		Y j ( t +1 )		Y m ( t + 1 )
S 0 ( t + 1 )	q 0,0	q 0,1		q 0, j		q 0, m
S 1 ( t +1 )	q 1,0	qv		q^j		q 1, m
S ( t +1 )	q j ,0	q j1		q j,j		q j , m
S m ( t + 1 )	q m ,0	q m ,1		q m , j		q m , m

оценки вероятностей переходов между состояниями. Введем правила для указанных переходов: r ( s j ( t +1 )) = Ф ( s j ( t ), x ( t )) - вероятность перехода в новое состояние, q ( у , ( t +1 )) = T ( s j. ( t +1 )) - вероятность появления выходного сигнала, где j = 1 , m, m - число состояний автомата, t = 0,1,2, ....

В начальный момент времени t автомат находится в состоянии S . . В этот момент времени выходной сигнал не вырабатывается. Для начального состояния задается распределение вероятностей перехода P _j во внутренние состояния S j ( t ). Начальное распределение состояний для примера приведено в таблице 1.

Начальное распределение вероятностей состояний формируется на основе априорной информации, которая может быть получена, например, в процессе нормального функционирования БТС при отсутствии внешних возмущений.

В таблице переходов задаются оценки вероятностей перехода в состояние Sk (t +1) в зависимости от состояния Sj (t) при условии поступления сигнала xi (t). Обозначим эту вероятность - j. В каждой строке матрицы вероятности перехода образуют полную группу: ^ r j k = 1. Ниже при-k=0

веден пример таблицы переходов (таблица 2) при входном сигнале x i ( t ) . Число таких таблиц равно числу состояний x i ( t ) .

Таблица выходов автомата Мура (таблица 3) упрощается по сравнению с автоматом Мили, так как выходной сигнал Y зависит только от внутреннего состояния S и не зависит от входного сигнала X. Обозначим qij – вероятность появления выходного состояния Yj (t +1) при условии, что автомат находился в состоянии Si (t +1), при m этом £ qi j = 1.

j = 0

Как и начальное распределение вероятностей состояния, матрицы ф ( S i j _k ) ^{и ф} ( S' , , j , k ) формируются на основе априорной информации в режиме обучения в процессе нормального функционирования БТС при отсутствии внешних возмущений.

В рабочем режиме функционирования БТС подвержен влиянию внешних воздействий, которые приводят к изменению значений априорных вероятностей. С целью учета влияния внешних факторов предлагается на основе апостериорной информации, получаемой в процессе контроля состояния ресурсов БТС, использовать адаптивную модель, базирующуюся на оценке однородности распределений числа «поощрений» («штрафов») для каждого элемента формируемых матриц SP ( Тнорм ) на этапе обучения и SP(Твнеш) в процессе контроля. В каждом такте автомат формирует сигнал поощрения (штрафа) в зависимости от выполнения условия: Sk (t +1) = = Sk (t). Если условие выполняется, то соответствующий элемент матрицы поощрения (штраФа) SPk (Тнорм) на этапе обучения или в рабочем режиме SPk (Твнеш) увеличивается на 1. При этом происходит перерасчет вероятностей матриц переходов по следующим формулам (модель Буша – Мостеллера [8]):

r ( t + 1 ) = в r ( t )/ ( 1 - ( 1 -в ) r ( t ) ) , (2) r j ⁽ t ⁺ 1 ) = r j ⁽ t )/^{( 1 -( 1 -p)} r k ⁽ t ) ) , j * ^k .

При получении сигнала «штраф» перерасчету подлежат вероятности по формулам (2), только вместо коэффициента β используется коэффициент α. Значения коэффициентов выбираются из условий: p > 1 , a < 1 .

В зависимости от оценки величины неоднородности матриц SP ( Т норм ) , SP ( Т внеш ) определяется принадлежность к одному из возможных классов. Величина неоднородности может быть получена при оценке дивергенции Кульбака – Лейблера [9] при сравнении указанных матриц. Переход системы в состояния S 0 , S 1 , S ₂ случайный, что имеет место, когда не осуществляется целенаправленного воздействия. Такое состояние ресурсов относится к нормальному состоянию БТС. Если матрицы (поощрений или штрафов) значительно отличаются друг от друга, то из этого можно сделать вывод, что состояние БТС подвержено внешнему воздействию – атаке.

^Введ^ем обозначение D ^{( SP(Т} норм X ^SP(Т внеш )) расхождения между двумя распределениями ^SP ( ^Т норм ) и ^SP ( ^Т внеш ) . Тогда Дивергенция определится как

n

D ( SP ( Т норм ), SP ( Т внеш ) ) = Z SP k ( Т норм ) Х к = о                    (3)

х ( 10g ( SP k ( Т норм )/ SP k ( Т внеш ) ) ) .

С целью сравнения оценок расхождений между распределениями на временном интервале Tнорм и исследуемым Tвнеш определим понятие зоны оценки величины расхождения для каждого состояния ресурса S0, S1, S2. Будем для определенности рассматривать следующие зоны клас- сификации: [0;Z 1), [Z1;Z2), [Z2;Z3]. В зависимости от принадлежности текущего значения расхождения D (SP(Тнорм X SP(Твнеш)) е Zi (i = 1,k) будем классифицировать следующие информационные состояния ресурсов на примере трех состояний:

D ( SP ( Т норм ), SP ( Т внеш ) ) < Z 1

– отсутствие расхождения (нормальное состояние),

Z 1 ^ D ( SP ( Т норм ), SP ( Т внеш ) ) < Z 2

– неустойчивая область (предкритическое состояние),

Z 2 ^ D ( SP ( Т норм ), SP ( Т внеш ) )

– наблюдение расхождения (критическое состояние).

Алгоритм классификации состояния ресурсов

БТС, принадлежащих каждому из возможных классов, содержит следующую основную последовательность действий.

– Задается начальное распределение вероятностей - P_нj , состояний переходов и выходов, значения n , m , V.

– Определяются вероятности переходов – r i j _k и вероятности выходов - q i j на этапе обучения автомата, формируется матрица поощрений (штрафа) ^SP k ( Т норм ⁾ .

• -    По значению входного сигнала x ( t i ) и состояния автомата S j ( t ) из матрицы ||ф ( S i j _k )|| выбирается строка r , j , ₀ , т ^, j , 1 , ^ , r , j , m .

• -    Разыгрывается вектор состояний S j ( t ) и выбирается элемент r i j _k, формируется новое внутреннее состояние S_k ( t +1 ) , k = 0,1 , ^ , m .

  – Выполняется проверка совпадений состояний автомата в соседние моменты времени, и формируются сигналы «поощрение» («штраф»):

• 1    SP k ( Т внеш ) = SP k ( Т внеш ) + 1

^SP k ⁽ t ⁺ 1М^если S k ( t +1 ) = S k ( t ) ;

0 , если S_k ( t +1 ) * S_k ( t ) .

– Выполняется перерасчет вероятностей по формулам (2).

• -    По значению S_k ( t +1 ) состояния автомата из матрицы ||т( Y i j )|| выбирается строка q j . ₀ , q j ,1 , ^ , q j , m .

• -    Разыгрывается вектор состояний S_k ( t +1 ) , и выбирается элемент q j _k, формируется новое выходное состояние Y_k ( t +1 ) , k = 0,1 , ^ , m .

План экспериментов включает задание априорных вероятностей P_нJ , P j _k , объема выборки – V , закона распределения генерируемой по-

Динамика состояний ресурса

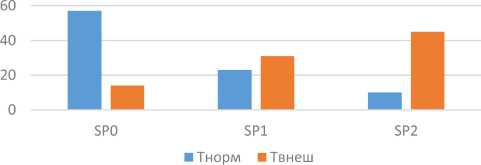
Рисунок 2. Динамика состояний ресурса, полученная в результате моделирования на временных интервалах T и T с указанием числа поощрений SP k (Т^ ), SIP ^(Т внеш )

следовательности, границ интервалов состояний и др. Основная цель – провести моделирование процесса обнаружения изменения состояния ресурсов БТС на основе апостериорной информации, определить оценки вероятностей появления состояний S 0 , S 1 , S 2 ; обеспечить поддержку принятия решения при оценке влиянии стохастической среды и внесении внешнего воздействия; с помощью критериев непараметрической статистики получить оценки влияния внешнего воздействия. Полученные статистические результаты экспериментов используются для выбора значений параметров модели с учетом конкретных условий различия состояний ресурсов.

На рисунке 2 представлены значения элементов матриц поощрения SP ( Т н _О р _М ), SP ( Т_внеш ), полученные в результате моделирования на интервалах ^Т норм ^и Т _вНеш . Причем на интервале ^Т внеш в поток данных были внесены возмущения [10], которые привели к увеличению предкритиче-ских, критических состояний и уменьшению числа нормальных состояний.

Заключение

В статье рассмотрен алгоритмический подход обнаружения уязвимостей интерфейсов БТС на основе самообучаемых вероятностных автоматов. Предлагаемый метод ориентирован на обнаружение изменения состояния контролируемых ресурсов БТС: канал связи, процессор, память. Метод базируется на применении адаптивной модели вероятностного автомата. Апостериорная информация о состоянии ресурсов в процессе функционирования БТС используется для адаптации к воздействиям внешней стохастической среды.

Предложенный адаптивный подход приведет к повышению достоверности и оперативности процессов поддержки принятия решений в задачах обеспечения безопасности объектов критической информационной инфраструктуры «Умный город».

Работа выполнена при частичной поддержке Российского фонда фундаментальных исследований (грант № 19-29-06015, 19-29-06023).