Адаптивная оптика реального времени для коррекции лазерного излучения в условиях сильной турбулентности

Исследование параметров атмосферы становится особенно актуально в связи с появлением различного рода систем, использующих в своей работе лазерное излучение. В связи с очень быстрым развитием и внедрением в жизнь современных беспилотных летательных аппаратов проблема передачи энергии лазерных пучков в условиях наличия атмосферной турбулентности становится особенно актуальной. Тут нужно отметить и задачи обеспечения коммуникации с беспилотными летательными аппаратами [1, 2, 3], включая низкоорбитальные спутники [4]. Также хорошо известно о необходимости «борьбы» с атмосферными помехами в задачах передачи криптографически защищённой беспроводной информации в турбулентной и рассеивающей среде [5– 12], а также организации оптических каналов связи в свободном пространстве [13, 14] и даже в разрабатываемых современных системах уничтожения космического мусора [15 – 17].

При прохождении лазерного луча сквозь турбулентную атмосферу Земли качество волнового фронта ухудшается, что приводит к ограничениям в работе различных систем и, в частности, даже невозможности сфокусировать лазерное излучение на объекте [18–30]. На сегодня, пожалуй, единственным методом решения данной проблемы является использование адаптивной оптической системы (АОС), позволяющей корректировать волновой фронт в реальном масштабе времени [31]. Задачи увеличения дальности распространения лазерного излучения сквозь атмосферу с применением методов адаптивной оптики решаются научными коллективами из России, Индии,

Франции, США, Австралии и др. [32–36]. Основным требованием к адаптивной оптической системе является частота коррекции. Поскольку, согласно [37] или [38], при некоторых «стандартных» погодных условиях частота изменений волнового фронта лазерного излучения, искаженного турбулентной атмосферой, редко превышает 100 Гц, скорость работы дискретной адаптивной оптической системы должна быть не менее 1 кГц [39].

Данная работа посвящена исследованию адаптивной оптической системы, созданной для компенсации фазовых флуктуаций, вызванных атмосферной турбулентностью, для её дальнейшего использования в системах передачи лазерного излучения вдоль горизонтальных или наклонных трасс. Использование лазерной трассы, работающей в реальных атмосферных условиях, достаточно затратно и трудоемко. Поэтому исследования были проведены на примере турбулентности, созданной в лабораторных условиях.

1.    Система стабилизации положения пучка

Для эффективной коррекции искажений светового пучка, распространяющегося сквозь атмосферу, необходимо оценить степень воздействия турбулентности на излучение. Как показано, например, в работе [40], распределение энергии по полиномам Цернике имеет вид, представленный на рис. 1.

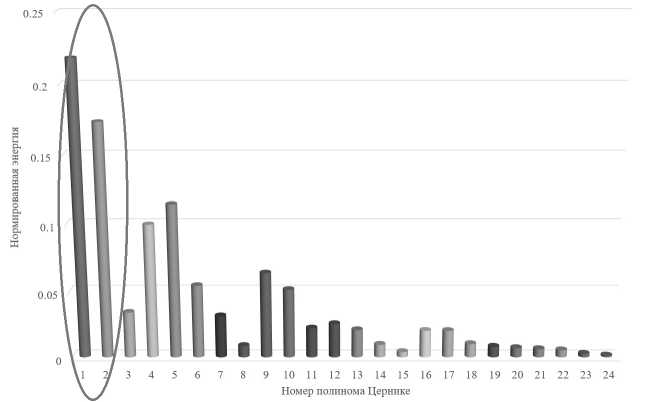
Рис. 1. Распределение энергии по полиномам Цернике

Нумерация полиномов Цернике выполнена согласно ГОСТ Р 8.745–2011 [41, 42]. Видно, что существенный вклад в состав аберраций волнового фронта вносят наклоны (полиномы Цернике номер 1 и 2), на долю которых приходится почти 40% всей энергии турбулентности.

Для коррекции наклонов предлагается использовать систему стабилизации положения пучка в пространстве, использующую два управляемых по наклонам зеркала. Положение пучка в пространстве измеряется с помощью двух квадрантных датчиков типа ФД-22-133К. Схема устройства показана на рис. 2.

Работа системы основана на том, что через две точки в пространстве можно провести только одну прямую линию. В данной конфигурации в качестве таких точек выступают центры датчиков положения пучка 1 и 2, через которые должен проходить световой пучок после проведения коррекции. Входящий световой пучок отражается от корректора наклонов 1 в направлении центра корректора наклонов 2, после чего направляется на датчики положения пучка. Также необходимо совмещение прямой линии, образованной центрами датчиков, с центром второго корректора наклонов, что достигается соответствующей юстировкой оптической части. Корректор наклонов 1 может располагаться более-менее произвольно, в его задачу входит направление входящего светового пучка в центр корректора наклонов 2.

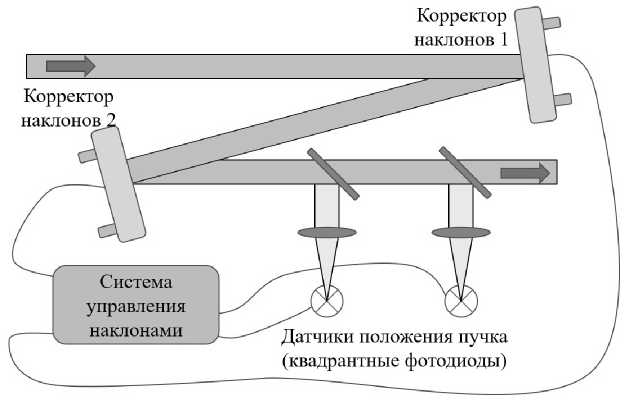
Рис. 2. Схема устройства стабилизации положения пучка в пространстве

Схема расположения и геометрические размеры светочувствительных площадок датчика представлена на рис. 3.

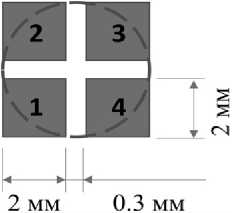
Рис. 3. Схема светочувствительных элементов квадрантного датчика

Пунктирной линией показано оптимальное расположение светового пучка, обеспечивающего наибольшую линейность датчика во всем диапазоне. Проверка линейности отклика квадрантного датчика осуществлялась при помощи математического моделирования. Предполагалось, что амплитуда отклика каждого сектора датчика пропорциональна площади, покрываемой световым пучком. Моделирование проводилось для разных диаметров светового пучка, результаты моделирования представлены на рис. 4.

Координаты пучка вычисляются по следующим формулам:

x =( I 1 + I 2 ) –( I 3 + I 4 ) /( I 1 + I 2 + I 3 + I 4 ),               (1)

y =( I 2 + I 3 ) –( I 1 + I 4 ) /( I 1 + I 2 + I 3 + I 4 ),               (2)

где I 1 ÷ I 4 – интенсивность сигнала соответствующего сектора датчика, x и y – нормированные координаты светового пучка в диапазоне (–1 ÷ +1).

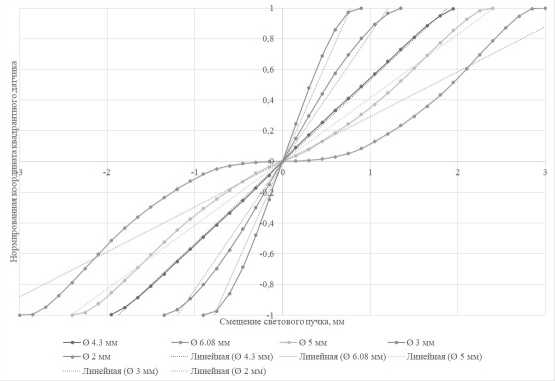
Рис. 4. Выходные характеристики квадрантного фотодиода в зависимости от диаметра пучка

Нормирование на сумму интенсивностей всех секторов датчика позволяет избежать зависимости координат светового пучка от изменяющегося уровня интенсивности.

Из рассмотрения графиков (рис. 4) видно, что наибольшая линейность квадрантного датчика во всем диапазоне смещений получается при диаметре светового пучка, равном размеру светочувствительных площадок плюс ширина зазора между площадками –4,3 мм. В оптической схеме требуемый диаметр пучка достигается с помощью использования масштабирующих фокусирующих линз и подбора расстояния между линзой и датчиком (рис. 2).

Достаточно большие размеры светочувствительных площадок были выбраны для того, чтобы максимально исключить дифракционные эффекты дальней зоны светового пучка (распределения интенсивности в фокусе масштабирующей линзы).

Управление зеркалами можно осуществлять с помощью алгоритма, основанного на функциях отклика (ФО) корректоров наклонов. Использование функций отклика позволяет автоматически учесть такие параметры системы, как чувствительность актюаторов корректоров наклонов, расстояния от корректоров до датчиков положения светового пучка, неточность ориентации корректоров и датчиков по линиям вертикаль-горизонталь (поворот относительно оси пучка), т.е. фактически провести калибровку всей системы. Для использования функций отклика можно записать следующую систему уравнений:

X 1 = « 11 • VX 1 + « 12 • Vy i + « 13 • Vx 2 + « 14 • Vy 2

^y 1 = « 21 • ^Vx 1 + « 22 • ^Vy 1 + « 23 • ^Vx 2 ⁺ « 24 • ^Vy 2

1                                                                                    , x2 = «31 • VX1 + «32 • Vy + «33 • Vx2 + «34 • Vy2

У 2 = « 4i • Vx 1 + « 42 • Vy 1 + « 43 • Vx 2 + « 44 • Vy 2

где x 1 , y 1 , x 2 и y 2 – смещения пучка по осям x и y на датчиках 1 и 2 соответственно, a ij – коэффициенты матрицы функций отклика управляющих элементов (актюаторов), Vx 1 , Vy 1 , Vx 2 и Vy 2 – напряжения на актюаторах корректоров наклонов 1 и 2.

Измерение функций отклика осуществляется поочередной подачей пробного напряжения на актюаторы зеркал. Например, подача напряжения Vx 1 на актюатор первого зеркала по оси x (при нулевых напряжениях на остальных актюаторах) позволяет определить коэффициенты a 11 , a 21 , a 31 и a 41 , подача напряжения Vy 1 – коэффициенты a 12 , a 22 , a 32 и a 42 и т.д. Пример измерения функций отклика приведен на рис. 5.

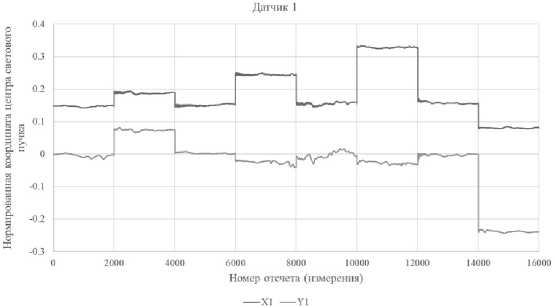
Рис. 5. Пример измерения функций отклика: координаты пучка на датчике 1

Ось абсцисс представляет номер отсчета (измерения), ось ординат – координаты, определенные по показаниям квадрантного датчика положения светового пучка № 1. Для повышения точности определения функций отклика используется усреднение измеренных значений при взятии N отсчетов. Так, в данном примере использовалось N = 2000 для получения одного измеренного значения. График примера измерений функций отклика был получен без строгой юстировки датчиков и зеркал по линии вертикаль-горизонталь (рис. 6), т.е. и зеркала, и датчики были повернуты относительно оси распространения светового пучка на некоторый угол. Использование функций отклика в алгоритме вычисления управляющих напряжений позволяет полностью исключить ошибку, связанную с неидеальностью данной юстировки оптического тракта схемы.

Рис. 6. Неидеальность юстировки – поворот датчика относительно оси пучка (линии вертикаль-горизонталь)

Для нахождения управляющих напряжений по заданным смещениям пучка используется матрица, обратная матрице функций отклика:

| V |=| A | ^–1 • | ds |,                                                  (4)

где | V | – вектор напряжений, | A | ^–1 – матрица, обратная матрице функций отклика | A |, | ds | – вектор смещений координат светового пучка.

Для проведения экспериментов были созданы корректоры наклонов, фотография представлена на рис. 7.

Рис. 7. Фотография корректора наклонов волнового фронта в карданной оправе

Основные характеристики корректоров наклонов сведены в табл . 1.

Табл. 1. Основные параметры корректора наклонов

Параметр	Значение
Диаметр зеркала	50 мм
Покрытие	Серебро с защитным слоем
Тип оправы	Карданная
Угол наклона	± 1000 мкрад
Первый резонанс	1500 Гц
Емкость актюаторов	1 мкФ
Число актюаторов	4

Для исследования работы стабилизатора положения пучка была собрана установка, соответствующая рис. 2. Турбулентность воздушного потока создавалась при помощи тепловентилятора, воздушный поток которого был направлен горизонтально. При проведении экспериментов была взята выборка координат положения светового пучка с датчиков длительностью около 8 секунд, при этом было записано 4096 отсчетов (2 ¹² , для последующего анализа с помощью быстрого преобразования Фурье). Частота взятия выборок при этом составляла 542 Гц. Рис. 8 иллюстрирует фрагмент выборки длительностью 0,2 секунды. Плавность перехода графика от одного отсчета к другому показывает, что частота взятия выборок достаточна для отслеживания изменения положения пучка во времени.

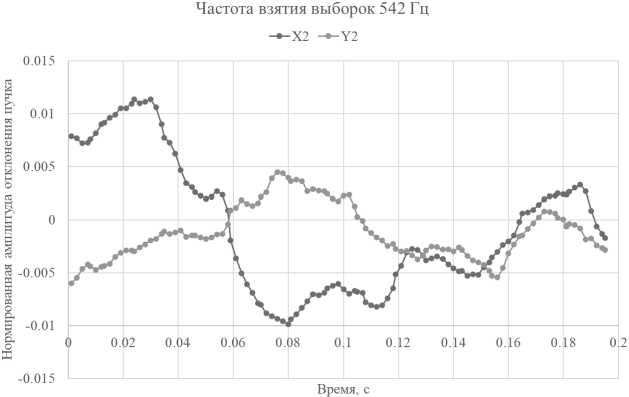
Рис. 8. Пример выборки по времени смещений пучка на датчике 2 по двум осям

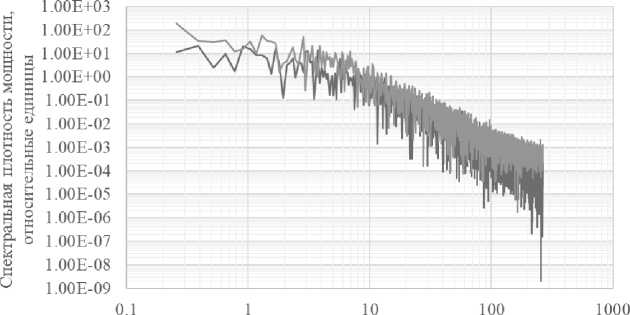
На основе выборки по времени с помощью быстрого преобразования Фурье была получена выборка по частоте, соответствующая спектральной плотности мощности процесса (рис. 9). При этом разрешение в частотном диапазоне составляло порядка 0,13 Гц, а ширина рассматриваемого спектра, соответственно, порядка 270 Гц.

Спектральная плотность мощности

—Y2 —Х2

Частота, Гц

Рис. 9. Спектральная плотность мощности изменения координат пучка (на основе данных с датчика положения пучка 2)

Проводя интегрирование спектральной плотности мощности, можно получить график спектральной энергии, который представлен на рис. 10. Кривые на данном графике приходят в насыщение на частоте порядка 10 Гц, что позволяет определить ширину полосы частот искажений наклонов волнового фронта.

Нормированная спектральная энергия

--Y2 --Х2

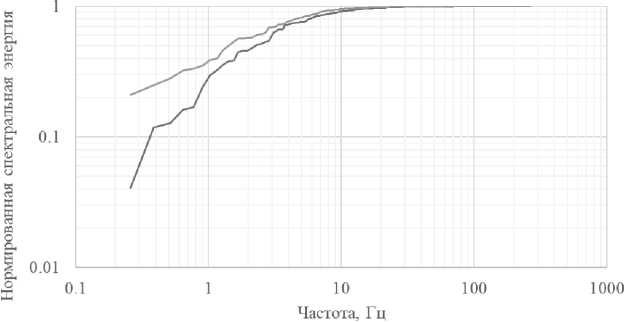
Рис. 10. Спектральная энергия изменения координат пучка (на основе данных с датчика положения пучка 2)

Таким образом, дискретная система стабилизации наклонов должна работать на частотах приблизительно в 10 раз выше, т.е. на частоте приблизительно 100 Гц. График (рис. 11) иллюстрирует работу системы стабилизации положения пучка на частоте 100 Гц. Видно, что данная частота достаточна для осуществления коррекции. На графике приведены смещенные координаты положения пучка, полученные по результатам измерений датчиков 1 и 2. В момент времени, соответствующий приблизительно 3,2 секунды, включается алгоритм коррекции, после чего смещения координат стремятся к нулю, что го- ворит о достижении цели стабилизации положения светового пучка.

Частота коррекции 100 Гц

■dXl --dYl --dX2 --dY2

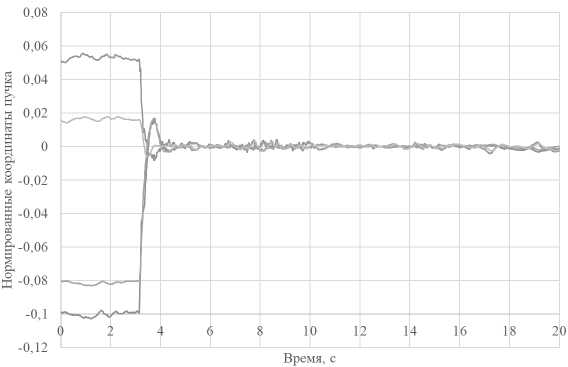
Рис. 11. Иллюстрация процесса стабилизации положения пучка

Применяя статистическую обработку к выборке, можно найти СКО (среднеквадратичное отклонение) остаточной ошибки коррекции. Для координаты x 1 СКО составляет 8,8 • 10 ^–4 , для y 1 – 1,2 • 10 ^–3 , для x ² – 7,2• 10 ^–4 , для y 2 – 9,0• 10 ^–4

2.    Коррекция аберраций волнового фронта с помощью быстрой АОС

Как показано, например, в [38], частота аберраций волнового фронта находится на уровне 100 Гц, следовательно, для эффективной коррекции таких аберраций частота работы системы должна быть не менее 1000 Гц. Для достижения такой частоты работы была использована программируемая логическая интегральная схема (ПЛИС), в частности, программируемая пользователем вентильная матрица (ППВМ). Схема экспериментальной установки быстрой АОС представлена на рис. 12.

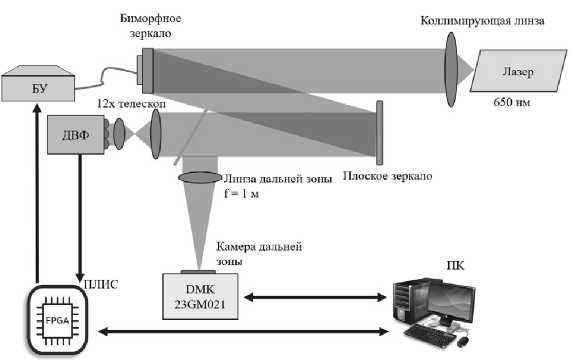
Рис. 12. Схема установки для исследования быстрой АОС (обозначения на рисунке: ПК – персональный компьютер, БУ – блок управления адаптивным зеркалом, ДВФ – датчик волнового фронта, ПЛИС – программируемая логическая интегральная схема)

Излучение лазерного диода, сопряжённого с волокном, при помощи линзы коллимируется в пучок диаметром 50 мм и попадает на биморфное зеркало – корректор волнового фронта. После отражения от корректора через светоделитель часть излучения отводится на датчик волнового фронта Шака–Гартмана. Управление замкнутым циклом коррекции осуществляется с помощью ПЛИС. Для независимой оценки качества коррекции используется индикатор дальней зоны, образованный с помощью длиннофокусной линзы (f = 1 м) и камеры с мелким размером пикселя для получения более детального изображения распределения интенсивности в дальней зоне. Основные результаты исследования АОС представлены в работе [43]. Быстрая АОС на основе биморфного корректора не способна корректировать наклоны волнового фронта, поэтому был проведен ряд экспериментов по исследованию совместной работы системы стабилизации положения пучка в пространстве и быстрой АОС (рис. 13).

Стабилизатор положения пучка Адаптивная оптическая система

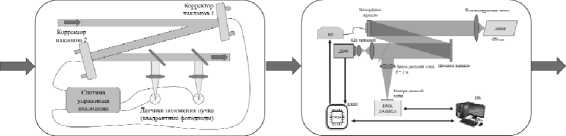
Рис. 13. Совместное использование стабилизатора положения пучка и быстрой АОС

В качестве корректора волнового фронта использовалось биморфное деформируемое зеркало диаметром 50 мм [44], структура электродов которого показана на рис. 14. Частота коррекции при проведении экспериментов достигала 2000 Гц (кадров в секунду).

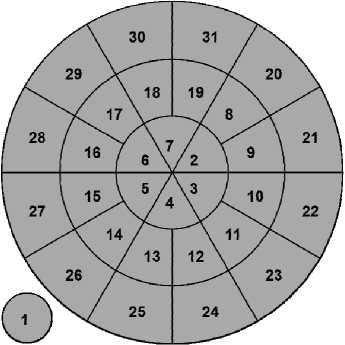
Рис. 14. Структура электродов корректора (1 – номер большого электрода, реализующего общий прогиб зеркала, 2 – 31 – номера внешних электродов, отвечающих за создание мелкомасштабных аберраций)

Наиболее наглядным является представление волнового фронта светового излучения в виде ортогональных в единичной окружности полиномов Церни-ке [41, 42]. Поскольку волновой фронт под воздействием турбулентности претерпевает изменения во времени, удобно использовать интегральное представление разложения, выполненное путем расчета эквивалента энергии, приходящейся на тот или иной полином Цернике [45]. Исходное (без коррекции) распределение энергии турбулентности волнового фронта представлено на рис. 1. После проведения коррекции волнового фронта (без коррекции наклонов) распределение энергии турбулентности по полиномам Цернике приобретает вид (рис. 15).

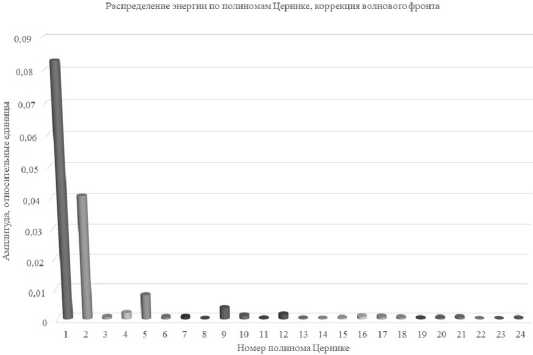
Рис. 15. Распределение энергии турбулентности по полиномам Цернике при коррекции волнового фронта (без коррекции наклонов)

Сравнивая рис. 1 и 15, можно увидеть уменьшение амплитуды основных аберраций после проведения коррекции волнового фронта. Но в то же время следует отметить, что АОС, использующая в качестве корректора биморфное деформируемое зеркало, не способна корректировать наклоны, поэтому интенсивность наклонов увеличивается по сравнению с исходными значениями.

Более удобной формой представления эффективности коррекции служит отношение исходной амплитуды заданной аберрации (полинома Цернике) к амплитуде, полученной после коррекции, выраженное в децибелах. Соответствующая диаграмма представлена на рис. 16.

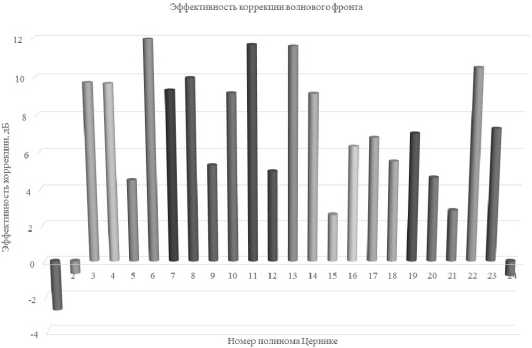
Рис. 16. Эффективность коррекции волнового фронта (без коррекции наклонов)

Положительные значения на диаграмме отражают уменьшения амплитуды заданного полинома, а отрицательные – её увеличение. По причине отсутствия коррекции наклонов отношение исходной амплитуды энергии наклонов к амплитуде после коррекции меньше единицы, и после перевода в децибелы данная величина становится отрицательной. Также отсутствует коррекция полинома № 24, соответствую- щего сферической аберрации 4-го порядка, что обусловлено ограниченной пространственной разрешающей способностью корректора волнового фронта.

Дальнейшие эксперименты были проведены при совместном использовании корректора наклонов и АОС. В результате после коррекции распределение энергии по полиномам Цернике выглядит следующим образом (рис. 17).

Распределение энергии по полиномам Цернике, коррекция волнового фронта и наклонов

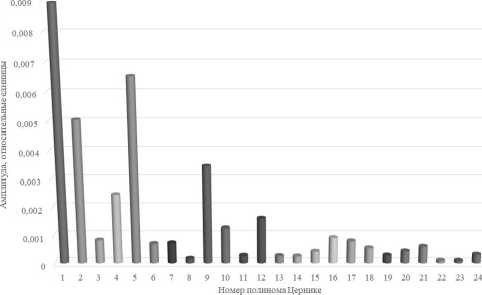
Рис. 17. Распределение энергии турбулентности по полиномам Цернике при одновременной коррекции волнового фронта и наклонов

Эффективность коррекции представлена на рис. 18.

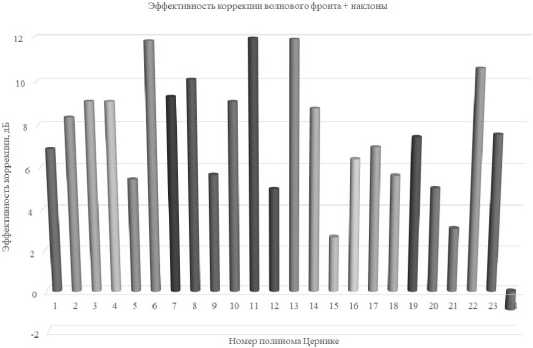
Рис. 18. Эффективность коррекции волнового фронта при одновременной стабилизации положения пучка

Сравнивая рис. 16 и 18, можно сделать вывод, что использование стабилизатора положения пучка позволяет существенно уменьшить амплитуду наклонов. В то же самое время коррекция остальных аберраций волнового фронта остается практически неизменной.

Заключение

Проведено исследование разработанной адаптивной оптической системы коррекции волнового фронта лазерного излучения, распространяющегося в условиях сильной атмосферной турбулентности. Показана эффективность стабилизации положения лазерного пучка в пространстве с помощью двух зеркал, контур управления которыми включает в себя два квадрантных датчика и ПЛИС. Показана возможность компенсации аберраций волнового фронта вплоть до 23-го полинома Цернике с помощью адаптивного зеркала, управляемого с помощью другой ПЛИС на основе информации с датчика Шака– Гартмана. В лабораторных испытаниях был задействован тепловентилятор в качестве источника атмосферной турбулентности. Ширина полосы возмущающего воздействия искусственной турбулентности в экспериментах не превышала 100 Гц. Это соответствовало среднестатистическому состоянию реальной атмосферы. В работе приведены результаты компенсации волнового фронта на частотах до 2000 Гц. Показано, что 10-кратное увеличение частоты коррекции волнового фронта по отношению к ширине полосы частот возмущающего воздействия обеспечивает устойчивую коррекцию, и распределение интенсивности излучения в дальней зоне при этом приближается к дифракционному.

Работы по стабилизации лазерного пучка (часть 1) выполнены при поддержке РНФ в рамках гранта № 20-19-00597, эксперименты по исследованию искусственной турбулентности (часть 2) выполнены при поддержке государственного задания Министерства науки и высшего образования Российской Федерации (тема № 122032900183-1), эксперименты по созданию адаптивных зеркал выполнены в рамках научной программы Национального центра физики и математики (проект «Физика высоких плотностей энергии. Этап 2023-2025»).