Адаптивное беспоисковое управление насосным комплексом в условиях нестационарности

A.G. Lutov, , Novozhenin, , MIREA – Russian Technological University, Moscow, Russia

В процессе функционирования автоматизированных насосных комплексов (НК), предназначенных для реализации технологических процессов перекачивания жидкостей в различных отраслях промышленности, установках и устройствах, имеют место не только координатные (напор, расход), но и параметрические возмущения (нестационарные параметры), к которым, в частности, можно отнести изменения гидравлических сопротивлений сети, насоса, всасывающего (входного) трубопровода, а также колебания параметров перекачиваемой жидкости [1]. При определенных условиях данные параметрические возмущения приводят к появлению в НК локальных колебаний гидродинамического характера, способствующих возникновению или активизации таких нежелательных процессов, как, например, кавитация [2, 3]. Последняя служит источником разрушения рабочих органов, шумов, вибрации и пульсаций давления в системе и, как следствие, снижения производительности, уменьшения КПД, повышения износа и уменьшения срока службы НК [4].

В [5] представлены результаты исследования условий устойчивости и возникновения локальных колебательных процессов при автоматизированном прецедентном управлении НК на основе центробежных насосов (ЦН) с учетом канала байпаса [6, 7]. НК с ЦН получили широкое распространение в связи с выигрышными массогабаритными показателями, высокой производительностью, способностью перекачивать загрязненные среды [8]. Показано, что способ регулирования методом байпасирования путем перепуска части жидкости во всасывающую линию насосов образует дополнительный канал управления НК, реализуемый с помощью регулируемой задвижки. Это увеличивает пространство возможных состояний НК как динамического объекта управления и, соответственно, расширяет возможности формирования потенциальных прецедентов при выборе рациональных (безкавитационных) режимов его работы [9].

При э т о м н е обхо д им о о тме тить следующее обстоятельство: если управле н и е НК по к а н а лу час т о ты вр аще н ия Ц Н является координатным (сигнальным), то управление п о к а н а лу байпаса – это п а р амет р ическое у п ра вление , реализуемое путем изменения такого парам е тра , ка к с опроти в лени е ка нала байп а са . О тсю да сл едует, что организация данного параметрич еского у пр а влени я в авт о мати ч еско м режим е т р е б ует и с п оль зо вания со о т в етст ву ющи х ме тодов синтеза системы управле н ия, в ч астности в кла сс е адапт и вн ы х са м о н астраивающи х ся с и с те м .

Одни м из эфф е ктивн ы х п о д ходов к построению систем с нестационарными п а ра ме тр ами я в ля е тс я р е ализация их в к ласс е беспоисковых самонастраивающихся систем с эталон н о й моделью, получивших большое те о ретиче ское развитие и широкое практическое приме н е н и е д л я у п ра вле н и я нестаци о нарными об ъ ектами [10, 11] .

Д а лее рассмотр е но пос тр ое ние алгоритма адаптивного беспоискового пара ме три ч е с к о г о управле н ия НК в усл ов иях не с та ц ио н а рности его упомянутых выше параметров с использовани ем о д ного и з д ос та точ но э ф фек тивных для этого подходов на базе градиент ного ме тод а с и нтез а ст р укт у ры с ам о настраивающейс я системы (СНС) с эталонной моделью [10, 1 1 ] .

Математическая модель насосного комплекса

В р або т е [ 5 ] п редс т авле н а м атематическая модель НК с учетом канала б айпаса, п о лу ч ен н а я н а осно ве ме то да эл е к тр оа н а лог ии [12, 13]. Применение данного подхода да ет в озможнос ть и с следо ва н и я различ н ог о ро д а д ин амических процессов в НК, анализа их устой ч и во сти.

При это м для иссле до ва н и я динамических процессов в НК на основе мет одо в те ор и и автом а ти че ского управле н ия п р и мен ительно к линейным системам [14] использ ова н а л и неа р изаци я напорно- р а с х одно й х ар ак терист ики (НРХ) в области ее рабочей точки с цель ю полу чения диф ф е ренц и альн ы х соп ро тив ле н и й элем е н тов НК:

R с =

dQ

> 0; R цн

Q 0

dHцн dQ

Q ₀

< 0,

где H _цн – н а пор, р а зви ва е мый ЦН ; H _с – напор гидравлической сети; Q – расход жидкости в системе; R _с – д и фф е ренциа л ьное с о проти в л ен ие се т и; R _цн – дифференциальное сопротивление ЦН.

Пре дп олаг а я , ч то в модели [5] в первом приближении учитываются толь к о д ифф е ренциал ьные сопротивления элем ен тов НК , данная исходная модель представлена на рис. 1.

На рис. 1: E – электрический эквивалент напора, развиваемого ЦН; I – электрический экви- валент расхода; Rс , Rцн , Rвх , Rб – эквиваленты дифференциальных гидравлических сопротивлений сети, центробежного насоса, всасывающего (входного) трубопровода, байпаса с регулируемой задвижкой (соответственно).

В соответствии со 2- м за к о но м Кирх г оф а у р а в н е н и е дл я эл е кт р ич е ско й ц е п и в компл е ксной ф о рме будет иметь вид:

E ( j m ) = I ( j m ) R „ + R ' ⁽ R ^{вх +} R ^c) цн

.

_ ^R б ^{+ R} вх ^{+ R} c

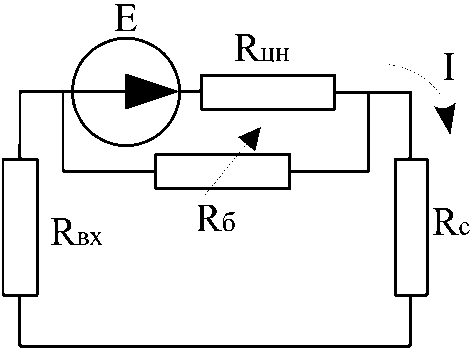
Рис. 1. Модель насосного комплекса, построенная на основе метода электроаналогии

Fig. 1. Model of the pumping complex based on the electroanalogy method

После перехода к опе р ат о рно й фо р ме за п и с и ( p = j m , где p - оп ера то р Л ап л аса ) модель НК можно п редс т авить в вид е п е р ед а точн о й ф у нкци и :

W ( P ) =

I ( p ) E ( p )

R^ ■ ( R bx + R c) б вх с

R цн +--

R + R + R вх с

^R цн ⁺     1       1

--1--

R + R  Rg вх с

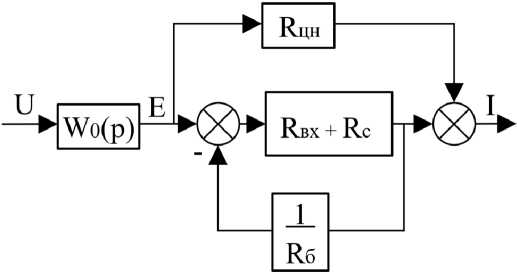
Рис. 2. Структурная схема системы управления НК

Fig. 2. Block diagram of the control system PS

Соответствующая структурная схема системы управления представлена на рис. 2. Здесь передаточная функция W 0 ( p ) отражает учет динамики привода ЦН, а также инерционность средств измерения выходной координаты системы и является по сути неизменяемой (в процессе управления) еe частью.

Компенсация изменений во времени дифференциальных сопротивлений Rс , Rвх , а также Rцн возможна, согласно выражению для передаточной функции (2), путем перестройки значения сопротивления бай- паса Rб , которое на практике осуществляется автоматизированной регулируемой задвижкой [15].

Для удобства дальнейших выкладок заменим значения сопротивлений на эквивалентные значения проводимости:

G™ = —; G_o =-- ¹--; G e = —

.

цн R„H о  RBX + R 6R цн            вх     сб

В этом случае передаточная функция (2) примет вид w (p) = 1—4—.(3)

С цн G o + G 6

Так и м обра зом , комп е н с ац и я в озможн ой н е с та ц и о н а рн ос ти п а раметров НК, в частности значения G _о , б у д е т п рои з в одить с я путем перестройки значения проводимости байпаса G _б .

Синтез алгоритма самонастройки

Для построения алгоритма перестройки Gб воспользуемся градиентным методом синтеза структуры СНС с эталонной моделью [10, 11].

В к а чес тв е э та л он ной моде ли выберем звено, описываемое передаточно й фун к ц и е й:

Wm (P) = ^ = Wo (P) • 1---Ц---,

U(P)            1 +

Gцн Go + Gб где Iм – выходная координата модели; Gц0н , Gо0 , Gб0 – некоторые базовые (желаемые) значения проводимостей Gцн , Gо , Gб .

Согласно методу градие нта , а лг ори тм п е р е с тройк и значе н и я G _б должен обеспечивать такое и зме н е н и е в ыбра н н ого к ри те ри я к а чест в а ра б от ы с и с те мы J , которое было бы направлено в стор ону е го у ме н ьш ени я, к ак фу н к ц и и G _б :

dG ₆   . d J

----= -K----, dt      dGб где J – показатель качества на основе меры рассогласования движений системы и модели, в качестве которой выберем функцию от ошибки 8 = i(t) - iM (t):

J = 8 2 = ( i ( t ) - i m( t ) ) 2 .

Исходя из выр а ж е н и я (5) , н а й д ем :

д J     д 2 „де

_ s = 2 s      .

д G б д G б        д G ₆

С учетом того, что i _м , u и W 0 ( p ) не зависят от G _б , получим следующее выражение:

де

' G

^( i - i ) _ д i = д [ ^ о ( p ) • W ( p ) ] д G _б '    ^?м^ д G б          д G б

д W ( p )

• ^u = ^Wo ( P ) „_   • u .

^{д G} б

Здесь д W (p)   д__1

д G б "д G 6 J_ ₊    ¹

. G цн   G o + G б.

^G цн   G o ^{+ G} б

• ^{( - )}

^G о ^{+ G} 6

_ w 2( p ) •

Тогда в ыраж е н и е (8) п риме т в и д :

dG^ _ - 2 Xs W o ( p ) W ² ( p ) • dt

-JL_

G o + G ₆ J

^G о ^{+ G} 6

• u _ - 2 Xs W ( p )

G o + G 6

• i.

В с оотв е тст в и и с п ре дп оложением, что в процессе функционирования СН С оп е ра тор с и с те-

мы д о лже н п одд е р жи в а ть с я б ли зк и м к оп е ра то ру модели, можно считать передаточную функцию

W ( p ) ® W _M ( p ), а также, что

^G о ^{+ G} б

G о ⁰ + G 0

Тогда dG^ = -X' е Wm( p) • x, dt

где X ' = 2 X

G О + G б

С тру к ту рн а я с хе ма са мон ас тра и в а ю ще й с я с и с т е мы с к он ту ром с а мон а с т ройки, функционирующим в соот в ет стви и с ан а ли ти че ск и м а лг ори т мом ( 11) , п р е дставлена на рис. 3. Зд ес ь д и н а ми че ское 1

звено         в к он ту ре ада п та ци и, с оо т-

Т б p + 1

в ет ству ю ще е п ози ц и онному и с п ол нительному у ст р о йст в у дл я пер ест р о йки G _б , уч и т ы вает ег о р еал ь н ую инерцио нно ст ь, им еющую м ест о пр и р абот е авт о м атиз ир ованной регулируемой задв иж ки байпаса.

Численное моделирование

С ц е л ь ю и сс ле дов а н и я р а б отос п о с об н ости си нтез и ров а н н ой С НС с э та лон н ой моде ль ю п рои зв е де н о ее чи с ле н н ое мо д е л и ров а н ие в у с лов и ях д е й с тв и я п а ра мет р ичес к и х в озм у щ ени й раз л ичн ого харак-

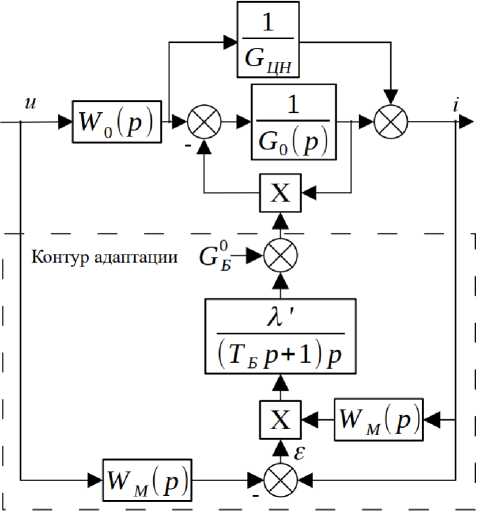
Рис. 3. Структурная схема СНС с эталонной моделью Fig. 3. Structural diagram of the SAS (self-adjusting system) with a reference model

тера. В качестве последних рассматривались изменения дифференциальных гидравлических сопротивлений сети Rс и входного трубопровода Rвх (или соответствующей величины проводимости G =-------). Численный эксперимент осуществлялся с использованием про-

О R вх + Rc граммной среды SimInTech, соответствующая компьютерная модель СНС приведена на рис. 4. Там же расположена модель системы без адаптации для сравнительного анализа переходных процессов. Значения параметров элементов модели представлены в таблице.

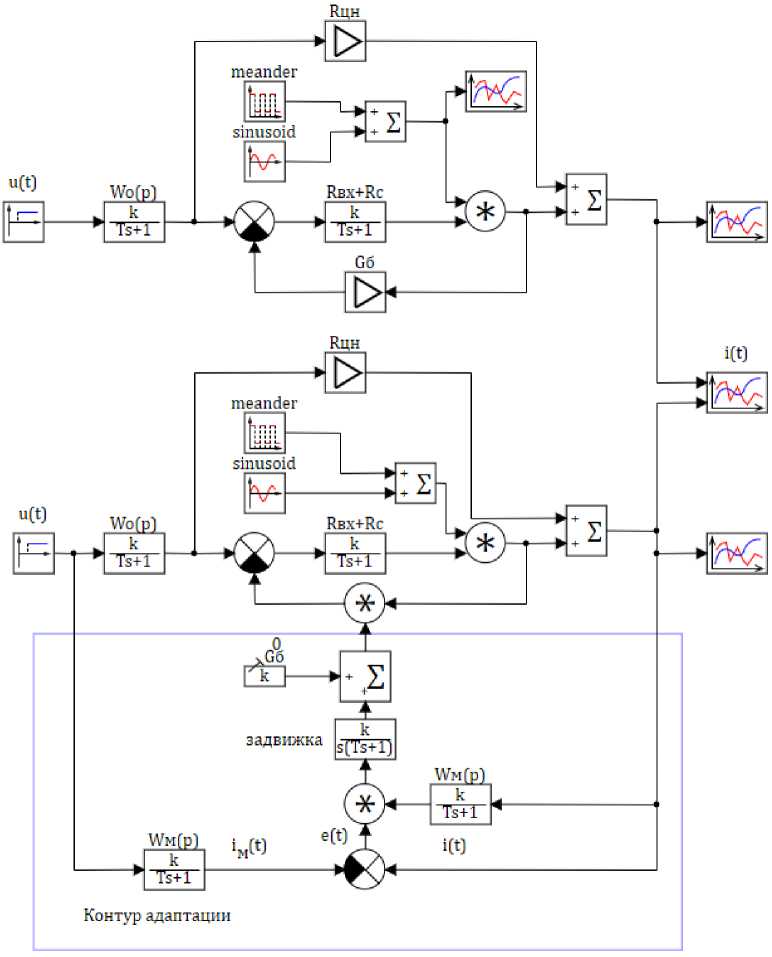
Рис. 4. Компьютерная SimInTech-модель СНС Fig. 4. Computer SimInTech model of the SAS

Значения параметров элементов модели Model element parameter values

Параметр	G о	G о 0	G цн	0 G цн	G б	0 G б	T 0	Т б
Значение	1	1	–0,33	–0,33	1	1	0,1	0,02

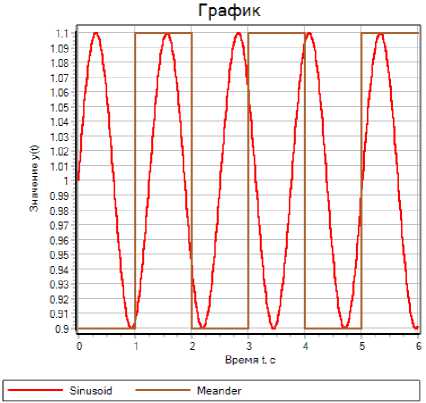
Результаты численного моделирования динамических процессов в СНС в окрестности рабочей точки НХР НК при параметрических возмущениях в виде изменений G _о периодического (синусоидального) и ступенчатого приведены на рис. 5.

а)

b)

Г рафик

c)

d)

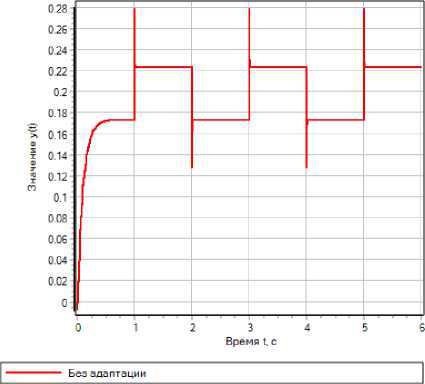
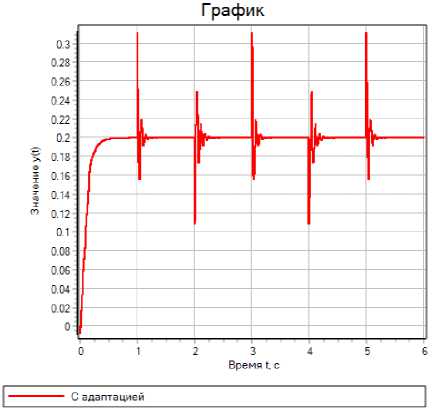
Рис. 5. Графики переходных процессов в СНС при отработке параметрических возмущений Fig. 5. Graphs of transients in the SAS during the processing of parametric perturbations

На рис. 5а приведены графики изменений проводимости G = , соответствующие о R вх + Rc параметрическим возмущениям синусоидального и периодического ступенчатого (меандр) характера соответственно. На рис. 5b представлены графики, иллюстрирующие отработку системой параметрических синусоидальных возмущений при отключенном и включенном контуре адаптации. Аналогично на рис. 5c и 5d приведены графики при действии на систему параметрических периодических ступенчатых возмущений также при отключенном и включенном контуре адаптации.

Обсуждение результатов

Для построения математической динамической модели НК использован метод электроаналогии, который позволил затем перейти к аппарату передаточных функций и исходному структурному представлению системы управления (см. рис. 2).

Синтезированный далее алгоритм управления беспоисковой СНС с эталонной моделью основан на градиентном методе синтеза структуры СНС (см. рис. 3) и использовании автоматически регулируемого канала байпаса НК.

Необходимо отметить, что быстродействие процессов регулирования по каналу байпаса изначально принципиально выше, чем быстродействие по каналу частоты вращения ЦН, так как их инерционность различается как минимум на порядок и более. Поэтому скорость отработки рассматриваемых параметрических возмущений в первом случае будет, безусловно, значительно больше.

Полученные в результате численных экспериментов с использованием компьютерной модели (см. рис. 4) графики переходных процессов в системе (см. рис. 5) свидетельствуют о работоспособности синтезированной СНС, высоком качестве отработки в ней как плавных периодических, так и ступенчатых (в том числе периодических) параметрических возмущений.

При этом устойчивость процессов самонастройки в построенной адаптивной системе может быть обеспечена выбором подходящего коэффициента передачи λ ` при численном моделировании процессов в СНС.

Заключение

Осуществлен синтез алгоритма управления беспоисковой самонастраивающейся системы с эталонной моделью для решения задачи отработки параметрических возмущений в насосном комплексе с использованием автоматически регулируемого канала байпаса.

Результаты анализа численных экспериментов подтверждают возможность построения и реализации адаптивной системы управления насосным комплексом для более эффективной (быстродействующей) автоматической отработки параметрических возмущений, обусловленных, в частности, изменениями гидравлических сопротивлений сети, насоса, входного трубопровода, а также колебаниями параметров перекачиваемой жидкости.

Применение адаптивного управления с использованием регулируемого канала байпаса позволит повысить эффективность координатно-параметрического управления НК в целом, особенно в условиях нестационарных гидравлических процессов: вибраций, элементов гидроудара, помпажа, кавитации.