Адаптивное итерационное управление температурой в теплице

Процесс изменения микроклимата теплицы является многоконтурным, многопараметрическим и зависит от множества внешних и внутренних факторов [1; 2]. К внешним факторам относятся температура и влажность наружного воздуха, интенсивность солнечного излучения, направление и скорость ветра и т. п. К внутренним факторам относятся геометрические размеры теплиц, расположение элементов систем отопления и вентиляции, виды грунтов, генетические свойства и виды растений и т. п. Кроме того, в замкнутых контурах управления микроклиматом каналы управления могут значительно влиять друг на друга. Для учета этих факторов задачу управления микроклиматом целесообразно решать на основе современных методов теории автоматического управления1.

Для иллюстрации предлагаемого адаптивного итерационного алгоритма управления стоит рассмотреть канал регулирования температуры теплицы с отоплением горячим трубным водоснабжением, которое применяется в северных регионах, где наружная температура меньше требуемой для создания микроклимата внутри теплицы. На основании закона сохранения тепловой энергии приближенная модель изменения температуры в теплице в зависимости от управляющего и основных возмущающих воздействий представляется в работах ряда исследователей [2–6] уравнением:

o kdt- = к Г + к (0° - 0") -T            cc      OT çàä

• - к ( 0 " - 0 " ) - кЕ ,        (1)

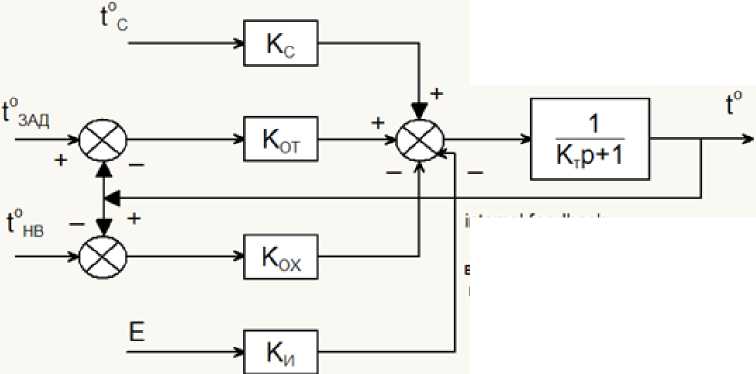
ox             íâ           u где to – текущая температура воздуха в теплице; tзадо – температура труб или воды в системе отопления; tH°- температура наружного воздуха; t – время; kT – конструктивный коэффициент теплицы в кг/(Юс3), который определяется из выражения: kT = pCpVT I AT, в котором р -плотность воздуха в кг/м3; Сρ – удельная теплоемкость воздуха в Дж/(К∙кг); VТ – объем теплицы в м3; АТ - площадь теплицы в м2; kc ‒ коэффициент нагрева от солнца в кг/(Юс3); t° - температура воздействия от солнечного излучения; kОТ – коэффициент эффективности системы отопления в кг/(Юс3), который определяется по формуле: kOT = ChAh/ AT, где Сh – коэффициент преобразования тепла системы отопления Вт/(К∙м2); Ah - площадь нагревательных элементов м2; kох – коэффициент охлаждения в кг/(Юс3), который определяется двумя составляющими: kox = рСф (t) + + фсАс / An, где yv(t) - естественная вентиляция м/с; Ac - площадь стен и потолка теплицы м2; φс – коэффициент передачи тепла в окружающую среду Вт/(К∙м2); ku, Е – коэффициент и скорость транспирации воды соответствующих размерностей.

Уравнению (1) соответствует структура объекта управления ОУ (теплицы) (рис. 1), которая является структурно определенной, но неопределенной параметрически. Эта структура имеет один канал управления и три канала возмущений, распределенно влияющих на выходную координату, а также две внутренние обратные связи, что затрудняет использование этой структуры для исследования влияния управления и возмущений.

Цель работы заключается в повышении точности поддержания темпера-

internal feedback by temperature / внутренняя обратная связь по температуре

Р и с. 1. Исходная структура объекта управления

F i g. 1. The initial structure of the control object

туры воздуха в теплице, для чего решаются следующие задачи:

– приведение исходной модели ОУ (1) и соответствующей структуры (рис. 1) к виду, удобному для исследования влияния неопределенности параметров модели и возмущающих воздействий;

• – разработка алгоритма адаптации регулятора для структуры системы управления с учетом реальных элементов и запаздывания в передаче теплоносителя;

• - проверка работоспособности реальной САУ температурой в теплице путем компьютерного моделирования.

Обзор литературы

Наиболее распространенным на практике методом регулирования температуры в теплице является введение ПИД-регулятора в контур отопления [3; 11] из-за его простоты. Однако он имеет ограничения по качеству регулирования, так как не учитывает неопре- деленность параметров и действие возмущений. Применение искусственных нейронных сетей [8; 9] позволяет получить высокую точность регулирования, что сложно применимо на практике из-за необходимости обучения. Это касается использования достаточно сложных интеллектуальных систем [7; 10]. Применение математических моделей [11; 12] позволяет учесть некоторые нелинейности в динамике, но не учитывает неопределенность параметров. Методы адаптивного и модального управления2 применены в работах ряда ученых [7; 10; 13] для синтеза одноканального регулятора и в исследовании Д. Н. Герасимова и М. В. Лызлова [2] для синтеза многоканального регулирования микроклимата теплицы, где использованы беспоисковые алгоритмы адаптации на основе идентификации неопределенных параметров и оценки их состояния. Беспоисковые алгоритмы адаптации требуют значительных вычислительных ресурсов, так как для их реализации необходима достаточно полная информация о действующих изменениях параметров, возмущений и их принадлежности определенному классу.

В некоторых случаях для создания системы управления микроклиматом на основе общепромышленных SCADA-систем3, когда имеется возможность применения стандартного ПИД-регулятора, но или нет возможности реализации экстраполятора Смита [14] для компенсации транспортного запаздывания, или неизвестна точная структура модели объекта управления, требуется поддерживать состояние температурного режима с максимально высокими настроечными коэффициентами регулятора [15]. Некоторые SCADA-системы имеют средства для автоматической настройки ПИД-регулятора4, но в системах с большими транспортными задержками их работа не приводит к нужному результату. В условиях нестационарности объекта это может привести к срыву процесса управления в автоколебательный режим, что нередко наблюдается на практике.

Материалы и методы

Приведение исходной модели температуры воздуха в теплице (1) и соответствующей структуры ОУ к виду, удобному для исследования параметрической неопределенности модели и возмущающих воздействий, проделано путем формального алгебраического преобразования уравнения теплового баланса (1) и по правилам эквивалентных преобразований структурных схем линейных САУ В результате преобразований получена структура реальной системы управления температурой в теплице (рис. 2), в которой в более опре-

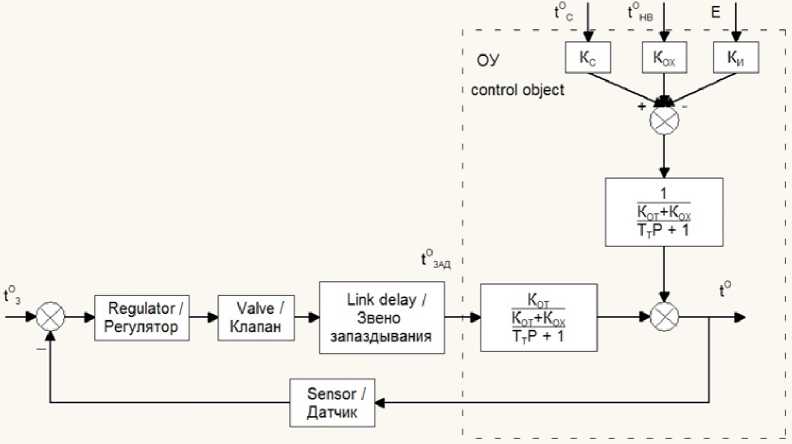
Р и с. 2. Структура реальной системы управления температурой теплицы F i g. 2. Structure of a real greenhouse temperature control system

деленной структуре ОУ сосредоточенно на выходную координату через апериодические звенья с постоянной времени T_T в секундах, равной отношению T t = k_T / ( k_or + к х ), действуют управление и возмущения, исключена внутренняя обратная связь, в канал управления температурой введены регулирующий, исполнительный и измерительный элементы, а также учтено запаздывание в движении теплоносителя.

На основе проведенного анализа существующих решений по синтезу САУ температурой в теплице в работе используется ПИД-регулирование в SCADA-системе с учетом запаздывания и адаптивный итерационный (поисковый) алгоритм подстройки ПИД-регулятора для компенсации про- извольных не заданных заранее параметрических возмущений. Применение итерационного (поискового) алгоритма адаптации обусловлено тем, что для реальных процессов как проектируемых, так и функционирующих, есть предварительная информация об управляемом процессе.

Структурная схема итерационного алгоритма определения параметров динамики процесса и подстройки коэффициентов ПИД-регулятора представлена на рисунке 3. В предположении, что в системе управления ведется база данных реального времени, которая содержит тренды управляемого процесса, можно применить адаптивный регулятор, использующий анализ этой базы данных. В его основе лежит оценка

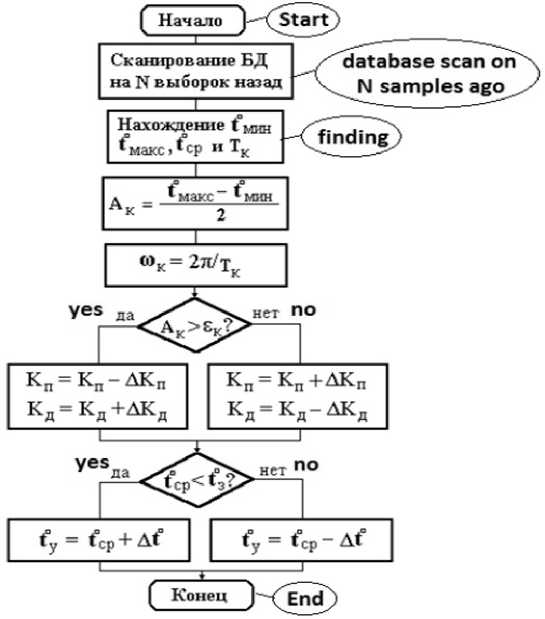
Р и с. 3. Алгоритм определения параметров процесса и подстройки коэффициентов ПИД-регулятора

F i g. 3. Algorithm for determining the process parameters and adjusting the coefficients of the PID controller

предыдущего состояния процесса регулирования. Если известна основная постоянная времени процесса регулирования T_o и период дискретизации T_д системы управления, то известно и количество записей в базе данных относительно текущего момента, которые могут дать информацию о ходе регулирования с числом выборок N = T_o / T_д. Используя или операторы языка СУБД или SQL-запросы, можно определить температуры t⁰_мин, t⁰_макс, t⁰_ср, период Т_к и амплитуду А к колебаний процесса регулирования.

Оценка качества процесса регулирования заключается в проверке, укладывается ли амплитуда колебаний Ак в пределы допустимой амплитуды εк и какова величина статической ошибки регулирования At0 = t03 - t0cp. По полу- ченной оценке производится коррекция коэффициентов регулятора Кп и Кд в сторону увеличения или уменьшения.

Одновременно вводится значение надбавки дополнительно к заданной температуре t⁰ = t⁰₃ ± At⁰ , чтобы компенсировать статическую ошибку. Одновременно проверяются допустимые границы изменения коэффициентов. Ввиду большого значения транспортной задержки применение интегральной составляющей регулятора ограничено и здесь не используется.

Результаты исследования

Для проверки поведения реальной САУ со структурой, приведенной на рисунке 2, с адаптивным итерационным регулятором составлена ее модель в пакете моделирования МВТУ (Sim-InTech)5 (рис. 4). На представленной адаптер/

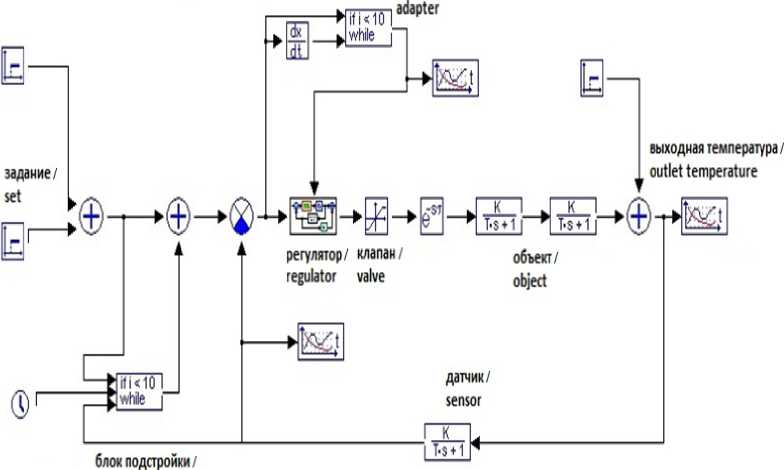
adjustment block

Р и с. 4. Модель адаптивной итерационной системы управления

F i g. 4. Model of adaptive iterative control system

[ETS]

модели блок адаптации БА производит поиск бесколебательной зоны управления в пределах допустимых изменений коэффициентов ПИД-регулятора.

Параметры модели следующие: t⁰_з = 20 ^оС, ПИД-регулятор, регулирующий клапан, представленным в виде звена с насыщением К_кл = 0,55. Задержка, обусловленная транспортным запаздыванием теплоносителя, τ = 240 с. Передаточная функция теплицы в канале управляющего воздействия представлена двумя апериодическими звеньями, первое из которых учитывает трубное отопление, а второе собственно теплицу по структуре рисунка 2. Коэффициент передачи теплицы, определенный по кривой выбега, К_т = 0,39, постоянная времени Т_о = 2400 с. Коэффициент передачи цепи обратной связи К_д = 1,0, постоянная времени обратной связи Т_д = 9 с.

Том 29, № 3. 2019

Так как процесс вхождения в бесколебательную зону может сопровождаться снижением пропорционального коэффициента регулятора и увеличением статической ошибки, то вторая составляющая блока адаптации, в виде программного блока, производит оценку ошибки и подстройку задающего воздействия через добавку ∆t^o.

Результаты моделирования при температуре 20 оС и дальнейшем ее снижении до 15 оС представлены на рисунке 5, там же показано влияние возмущающего воздействия на 10000-ной секунде процесса.

Обсуждение и заключение

Из полученных результатов моделирования видно, что подстройка коэффициентов ПИД-регулятора приводит к снижению колебательности процесса до допустимых пределов при повышении статической ошибки. Применение

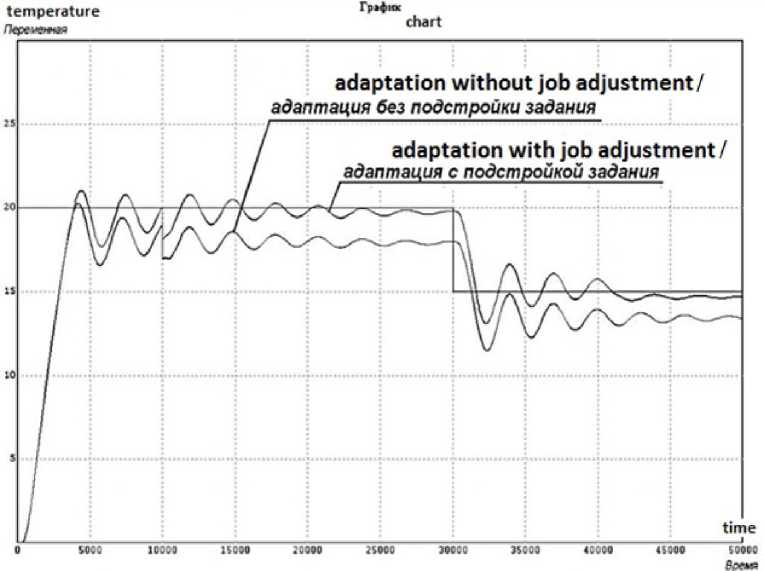
Р и с. 5. Результаты моделирования адаптивной итерационной системы управления

F i g. 5. Results of modeling an adaptive iterative control system

390                                        Процессы и машины агроинженерных систем

блока подстройки задающего воздействия эту ошибку устраняет, заставляя систему работать на грани перехода в колебательный режим. Таким образом, применение предлагаемого алгоритма адаптации в системе управления с большими транспортными задержками позволит избежать явления колебательности процесса, снизит износ регулирующего оборудования и повысит качество управления.

Предлагаемый алгоритм адаптации, заключающийся в аддитивной подстройке коэффициентов ПИД-регулятора, удобно реализуемый в SCAdA-системе, обеспечивает компенсацию неопределенности модели и возмущений, при этом достигается требуемая точность поддержания температуры в теплице. Результаты исследования послужат материалом для разработки многоконтурной САУ микроклимата теплицы с исследованием влияния и компенсации параметрической и структурной неопределенности, инер-ционностей и нелинейностей реальных элементов. Выводы работы могут быть использованы во многих отраслях народного хозяйства для исследования общих и прикладных проблем цифрового адаптивного управления процесса-ми6 с ПИД-регулированием координат [16], например, в системах управления интеллектуальными зданиями [17], в радиотехнике [18], в пищевой промышленности [19], в стройиндустрии [20], в производстве резинотехнических изделий [21] и т. д.

Поступила 17.12.2018; принята к публикации 18.02.2019; опубликована онлайн 30.09.2019

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.