Адаптивное обнаружение сигнала на фоне нестационарной помехи

Введение 1

В системах радиолокации (РЛС) важной зада-чей является стабилизация уровня ложных тревог (СУЛТ) [1, 2, 4, 5]. В условиях априорной неопре-деленности относительно параметров распределе-ния помехи СУЛТ может быть обеспечена приме-нением адаптивных параметрических алгоритмов обнаружения сигнала [1‒6].

Если помеха имеет стационарный характер, то реализация адаптивного обнаружителя не вызыва-ет особых затруднений, а качество его работы при достаточно большом объеме выборки мало усту-пает оптимальной обработке. В то же время неста-ционарность помехи может существенно снизить качество работы приемника [1, 4, 6]. Причиной нестационарности помехи могут быть как предна-меренные импульсные помехи, так и сигналы, от-раженные от целей, близкорасположенных к нс-следуемому элементу дальности РЛС.

Для уменьшения влияния мешающих сигна-лов на значение вероятностей ложного и правиль-ного обнаружения применяют специальные меры. Так,в [6] предлагается «метод контраста». Суть данного метода заключается в поочередном срав-нении отношений соседних выборок с некоторым порогом и удалении элементов выборки, не удов-летворяющих определенным условиям. Выбор оптимального значения порога проводится мето- дом моделирования.в [1] приводится структура адаптивного обнаружителя, в которой для умень-шения влияния близкорасположенных целей ис-пользуется ранжирование элементов выборки и вычисление порога обнаружения по элементу вы-борки из области больших амплитуд. Известны и другие способы повышения качества адаптивных обнаружителей в условиях мешающих сигналов [5]. Общими недостатками рассматриваемых адаптив-ных алгоритмов обнаружения являются относи-тельная сложность реализации и необходимость управления порогом обнаружения.

В настоящей статье исследуется простой ва-риант адаптивного обнаружителя с фиксирован-ным порогом, устойчивого к наличию нескольких мешающих интенсивных сигналов.

Постановка задачи

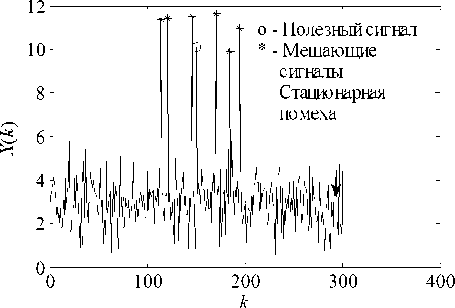
На вход цифрового обнаружителя поступает смесь стационарной помехи n ( k ), нескольких ме-шающих сигналов Si ( k ), i = 1… M И, возможно, по -лезного сигнала S 0( k ) (рис. 1):

H0 :X(k) M Si (k)  n(k), i1

H 1 : X ( k )    S 0( k )    ^M Si ( k )   n ( k ).

i 1

. 1.

Стационарная помеха n ( к ) является нормальным некоррелированным процессом с неизвест-ными средним т_п и среднеквадратическим отклонением (СКО) Оп- Амплитуды сигналов Ai ( i= 1...М) также неизвестны.

Необходимо предложить алгоритм обнаруже-ния сигнала S ₀( к ) c фиксированным порогом обнаружения , адаптивный к параметрам стационарной помехи и устойчивый к наличию нескольких ме-шающих сигналов.

Предлагаемое решение

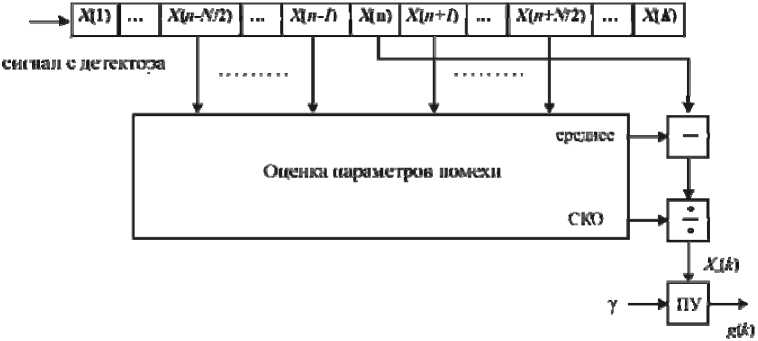
Рассмотрим схему простейшего адаптивного обнаружителя (рис. 2) [1, 2]. Отсчеты сигнала X ( к ) запоминаются в ОЗУ ( к = 1... K). Для отсчета X ( n ) по N - 1 соседним отсчетам, оцениваются среднее и СКО стационарной помехи ( N -1 - размер выборки). Далее величина X ( n ) нормируется путем вычитания оценочного среднего т_п и деления на оце-ночное СКО ст_п. Полученные таким образом отсчеты нормированной статистики X _H( n ) сравниваются с фиксированным порогом у. Порог у обеспечивает требуемое значение вероятности ложной тревоги PF .

Если в интервале дальности, соответствующем выборке помехи, мешающие сигналы отсутствуют , то выборка является однородной и качество работы обнаружителя зависит только от разме-ра выборки. Наличие интенсивных мешающих

сигналов в зоне выборки приводит к ошибкам в оценивании среднего и СКО стационарной поме -хи: оценки т_п и д_п смещаются в область больших значений. В результате вероятности PF (ложной тревоги) и PD (правильного обнаружения) снижаются . Уменьшение PF само по себе является желательным результатом. В то же время одновременное уменьшение величины P d говорит о снижении эффекта адаптации.

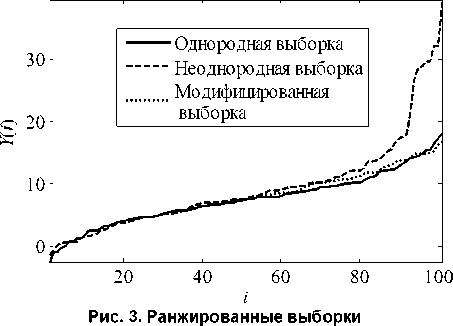
На рис. 3 изображена ранжированная выборка Y ( i ), i = 1... N -1, полученная из исходной выборки Xj ), j = ( n~N /2)^( n -1), ( n +1)^( n + N /2) путем расстановки элементов выборки в порядке возрас-тания. В случае однородной выборки X ранжированная выборка Y сходится к нечетной функции при N—> да. Наличие мешающих сигналов (неоднородная выборка) приводит к задиранию «хвоста» ранжированной выборки Y и в этом случае при N—>да Y к нечетной функции не сходится.

Поставленная задача может быть эффективно решена путем удаления из Y последних М элементов , где М - число мешающих сигналов. Но поскольку М - неизвестный параметр, такой путь

решения является затруднительным.

Суть предлагаемого решения состоит в еле -дующем. Нетрудно определить, что при малом

числе мешающих сигналов относительно размера выборки однородная и неоднородная выборки в среднем мало отличаются для i = 1...( N + 1)/2 (на рис. 3 N =101). Поэтому, используя первую половину Y ( i ), путем ее нечетного отображения можно получить модифицированную ранжированную выборку Y _M( i ), которая в среднем мало отличается от однородной выборки стационарной помехи.

При этом фактический размер выборки Y _M, по которой оцениваются параметры стационарной

помехи, уменьшается в два раза относительно ис ходной выборки А':

Y ( i ), i = 1.

Y _M ( i ) =

N + 1

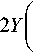
N + 1 _Y N + 1

2 J I 2

i

N + 3

N .

. 2.                                                                                (    ‒                                  )

Очевидно, что эффективность предлагаемого способа зависит как от размера исходной выборки, так и от относительного числа мешающих сигна-ЛОВ m = M / N .

Результаты моделирования

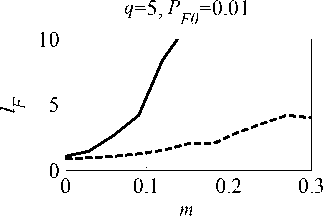
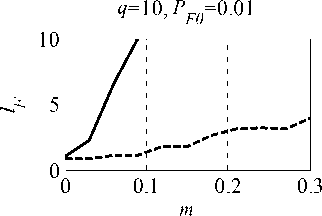
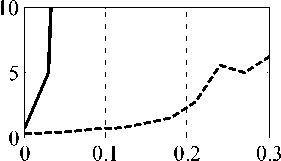
На рис . 4 изображены зависимости относи-тельного уменьшения вероятности ложной тревоги lF = PF0/PF (PF0 ‒ значение вероятности ложной тревоги, соответствующее оптимальной обработ-ке , PF ‒ фактическое значение вероятности ложной тревоги) от относительного числа мешающих сиг-налов m. Амплитуды мешающих сигналов в Jq раз превышают СКО стационарной помехи, пара-метры которой задаются случайным образом. Раз-мер исходной выборки 101. Представленные зави-симости получены методом статистического моде-лирования на ЭВМ (размер статистики 100/PF0).

Как видно , уже при 10 %-ном заполнении вы-борки мешающими сигналами P_F для исходного адаптивного алгоритма обнаружения может сни-зиться на порядок и более. В то же время примене-ние ранжирования выборки и преобразования (2) приводит к заметной СУЛТ: 20 %-ном запол-нении выборки мешающими сигналами P_F с нижа -ется менее чем в 3 раза.

Зависимости относительного уменьшения ве-роятности правильного обнаружения l_D = P_D 0/ P_D ( PD 0 ‒ значение вероятности правильного обнару-жения, соответствующее оптимальной обработке, PD ‒ фактическое значение вероятности правиль-ного обнаружения) от относительного числа ме-шающих сигналов m изображены на рис. 5. Ам -плитуды полезного и мешающих сигналов в Jq раз превышают СКО стационарной помехи. Раз-мер статистики при моделировании 1000.

Как видно , использование предлагаемого ал-горитма обнаружения препятствует существенно-му снижению P_D , которое имеет место в случае простого алгоритма адаптации, не учитывающего

q =10, P_F0 =0.001

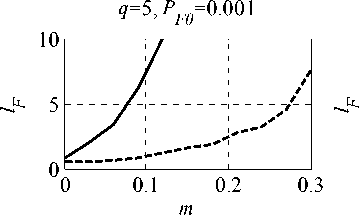
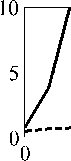
0.1       0.2       0.3

m

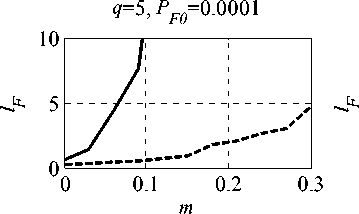
---Адаптивный

q =10, P_F0 =0.0001

m

• ■—Адаптивный с преобразованием выборки

Рис. 4. Зависимости l_F ОТ m

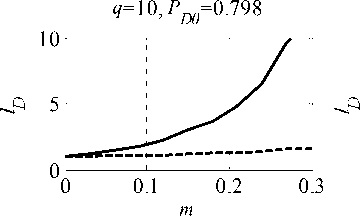
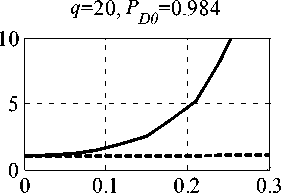
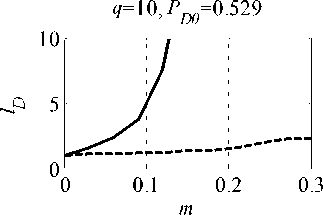
m

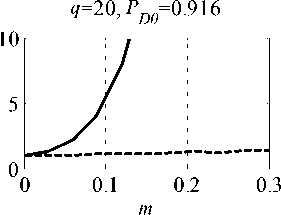
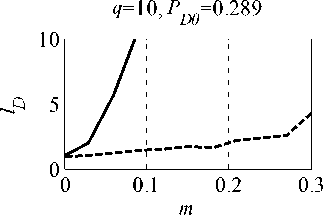
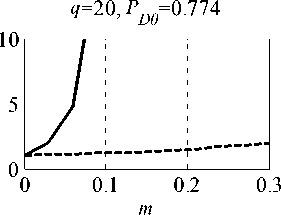
---Адаптивный ------Адаптивный с преобразованием выборки

Рис. 5. Зависимости lD ОТ m наличие мешающих сигналов : 20 %-ном за-полнении выборки мешающими сигналами PD снижается в 5 раз и более . Применение ранжиро-вания выборки и преобразования (2) обеспечивает снижение PD не более чем в 2 раза при m=0,2.

Заключение

Предложенный вариант адаптивного обнару-жителя позволяет повысить стабильность вероят-ностей ложной тревоги и правильного обнаруже-ния в условиях воздействия нормальной стацио-нарной помехи с неизвестными параметрами и наличия нескольких интенсивных мешающих сиг-налов. Количество мешающих сигналов, при кото-ром обеспечивается приемлемая стабильность ве-роятностей, составляет до 10‒20 % от размера вы-борки.

Рассмотренный вариант обнаружителя может быть полезен в задачах обнаружения-разрешения нескольких близкорасположенных целей. При этом каждый из сигналов Si ( k ), i =0… М может рассмат-риваться как полезный, а все остальные М сигна-ЛОВ ‒ мешающие по отношению к нему .