Адаптивное управление двигателем постоянного тока

Двигатели постоянного тока (ДПТ) имеют самое широкое распространение в промышленности. В ряде случаев их эффективное использование связано с устранением неопределенности о параметрах или внешних возмущениях, т. е. решением задачи адаптации.

В настоящее время известно большое количество методов решения задачи адаптивного управления двигателем постоянного тока, в том числе - частотные, геометрические, шунтирования, а также методы, основанные на использовании функций Ляпунова, итеративных процедур синтеза и т. д. [1]. В этом обширном арсенале заметное место занимают адаптивные системы с эталонной моделью (АСЭМ), которые относятся к классу систем прямого адаптивного управления [2]. Как правило, эталонная модель имеет простую структуру, это может быть, например, передаточная функция невысокого порядка. Механизм настройки параметров регулятора стремится минимизировать ошибку между выходом замкнутой системы y ( t ) и выходом модели y _m( t ):

e ⁽ t ) = У ⁽ t ) - У m ⁽ t ) ^ ⁰ -

Рассмотрим простой алгоритм адаптации, использующий так называемое правило MIT (от Massachusetts Institute of Technology ) [2, 3].

Определим целевую функцию, подлежащую минимизации, в виде:

J (0) = - e 2(0), где q – настраиваемые параметры. Таким образом, целевая функция всегда положительна, и уменьшение J(q) означает уменьшение e.

Правило MIT предполагает изменение пара- метров q в направлении антиградиента целевой функции:

d θ dt

, d J      ( d e

-k   = -y\ e д0     I d0

коэффициент у определяет длину шага в процессе минимизации.

Выбор константы у имеет большое значение для качества адаптации. Исследованию вопроса о рациональном выборе посвящен ряд публикаций [4 – 7].

В работе [4] исследуется влияние коэффициента адаптации у на параметры переходного процесса в системе второго порядка, экспериментально обосновывается выбор значения у , при котором минимизируется перерегулирование и время переходного процесса. В [5] подобное исследование выполнено для системы адаптивного управления двигателем постоянного тока. Настраиваемыми параметрами являются коэффициенты линейного ПИД-регулятора. Приведенные данные свидетельствуют о неоднозначном влиянии у на качество переходного процесса – сокращение времени нарастания связано с ростом перерегулирования. В работе [6] выполнен поиск оптимального значения коэффициента у при адаптивном управлении химическим реактором. В [7] рассмотрена задача использования АСЭМ при переменной инерции ротора ДПТ.

В работе [8] предложен линейный закон изменения коэффициента скорости адаптации, который вводится на основании функции Ляпунова, что гарантирует устойчивость переходного процесса. Рассмотренный пример адаптивной системы управления печатающим устройством показал значительное улучшение качества работы системы.

В работе [9] рассматривается система адаптивного управления ДПТ, который описывается как апериодическое звено 1-го порядка. Нелинейный коэффициент адаптации формируется с помощью таблицы нечетких правил типа Такаги – Сугено [10], посылками которых являются момент нагрузки и его производная, а заключением - коэффициент y. Всего используется 25 правил, настраиваемых методом проб и ошибок.

В данной работе рассматривается решение задачи управления коэффициентом скорости адаптации в схеме АСЭМ на базе генетически настраиваемой искусственной нейронной сети. Такая схема позволяет оптимизировать нелинейный закон изменения коэффициента у и повысить качество работы адаптивной системы.

СТРУКТУРА АДАПТИВНОЙ СИСТЕМЫ

J – момент инерции ротора, b – коэффициент вязкого трения, U - напряжение якоря, i – ток якорной цепи, M H - момент нагрузки, ю - угловая скорость вращения.

Рассмотрим задачу стабилизации скорости вращения вала двигателя при заранее неизвестных изменениях момента нагрузки. Из уравнения (1) можно получить описание наблюдателя нагрузки:

M _H ( t) = k to (t) - Ь б ( t) - J(6 ( t ),       (2)

где M H – оценка нагрузки на валу двигателя. Выберем закон управления в виде u (t) = 91 g (t) - 9 2 y (t).

Для объекта управления 2-го порядка закон адаптации имеет вид [1]:

d 9 1 dt

d e

■ y--- e = - y 5 9 1

1 d 9₂

—2 = y--e = Y dt     59 2

a i m s ⁺ a 0 m

< s ^{2 +} a i m s ⁺ a 0 m

d e

tii 5 “h tin

1 m      0 m

g ⁽ s ) ^e ,

( 5 + a im s + a о m

У ⁽ s ) ^e .

Рассмотрим применение модификации АСЭМ в задаче управления ДПТ. Математическая мо-

дель двигателя

Уравнения состояния ДПТ имеют вид:

ⁱ⁽ t )

6 ) ( t )

R

^^^^^^в

L k

J

k

• -    Z px t )

• -    b б t ) j _

+

L

⁰ г U ⁽ t ) ■

—1 [ M ( t )

J

где R и L – сопротивление и индуктивность якорной цепи, k – константа электродвижущей силы,

где 9 1 и 9 2 - настраиваемые параметры, a _1m и a _0m – параметры модели, g ( t ) – входной сигнал, Y - коэффициент скорости адаптации.

Предлагаемая модификация АСЭМ заключается в использовании переменного значения коэффициента скорости адаптации Y (t), для выработки которого применяется обучаемая искусственная нейронная сеть (ИНС).

Структура системы управления представлена на рис. 1 (где g ( t ) – заданное значение скорости вращения).

Наблюдатель нагрузки реализует формулу (2), а блок адаптации построен в соответствии с (3). Блок ИНС построен на базе нейронной сети прямого распространения.

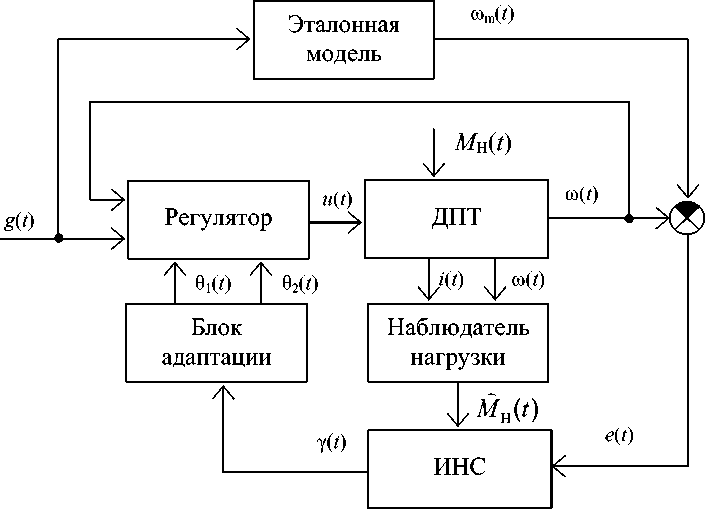
Рис. 1. Структура модифицированной АСЭМ

НЕЙРОННАЯ СЕТЬ ДЛЯ УПРАВЛЕНИЯ СКОРОСТЬЮ АДАПТАЦИИ

Задача управления скоростью адаптации имеет много общего с задачей разработки нейросупервизора для ПИД-регулятора [11], а именно – скорость адаптации должна зависеть от текущей ошибки и ее динамики, описываемой значениями интеграла и производной или их дискретными аналогами.

Структура ИНС была выбрана в соответствии с подходом, изложенным в [12, 13], предполагающим реализацию нейро-ПИД регулятора как трехканальной структуры с нелинейной активационной функцией и линейным весовым коэффициентом каждого канала. Специфика поставленной задачи требует также использования четвертого канала для подачи на вход ИНС значения оценки момента нагрузки.

На рис. 2 представлена структура ИНС при замене интеграла и производной их дискретными аналогами.

Матрица весов V здесь полагается заданной исходя из способа аппроксимации интеграла и производной ошибки [3, 4]:

11 10

V = 0 - 110

При описании активационных функций были сделаны следующие допущения:

Область определения и область значений активационной функции: [-1, 1].

Активационная функция нечетно-симметрична относительно начала координат.

Активационная функция допускает кусочнолинейное представление.

Нечетно-симметричная активационная функция занимает на плоскости 1 и 3 квадранты. Будем считать, что область определения функции разбита на равные отрезки ∆, тогда задача оптимизации заключается в выборе коэффициента усиления k _i= ∆ y _i/∆ для каждого отрезка. Пример разбиения базовой шкалы на четыре участка показан на рис. 3.

Существует большое количество алгоритмов оптимизации, большинство из них непрерывности и дифференцируемости целевой функции

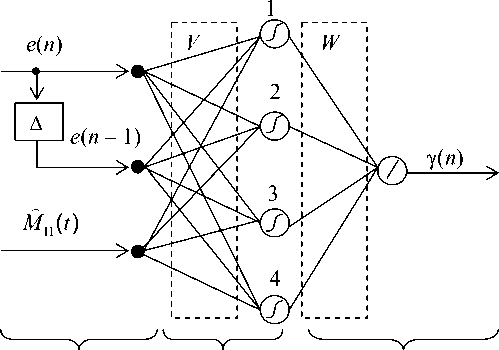
входной слой

1-й слой      выходной слой

Рис. 2. Структура ИНС

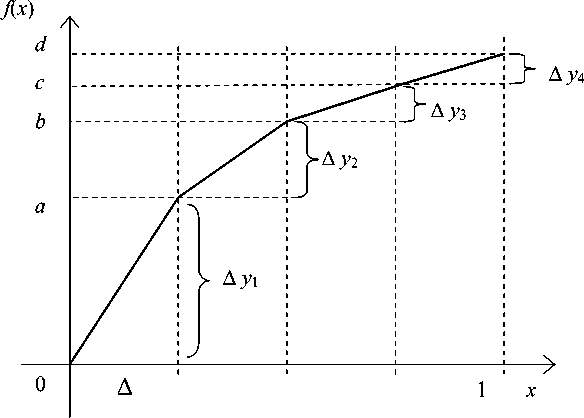
Рис. 3. Кусочно-линейное представление активационной функции

[14]. В рассматриваемой проблеме многоэкстремальный характер целевой функции требует использования алгоритмов глобальной оптимизации, таких как генетический алгоритм (ГА).

Вопросы применения ГА для синтеза регуляторов рассмотрены в [15 - 16]. Параметры регулятора кодируются хромосомой фиксированной длины, подсистема моделирования связывает с каждой хромосомой оценку пригодности (fitness function ). Набор хромосом образует популяцию, которая эволюционирует под воздействием операторов копирования, скрещивания и мутации.

При рассмотренном выше разбиении базовой шкалы каждая активационная функция имеет 4 параметра: P = { a 1 , b 1 , c 1 , d 1 }, так что, в совокупности с весовыми коэффициентами каналов, образуется хромосома из 20 генов, каждый из которых является действительным числом (рис. 4).

Минимизируемая целевая функция может быть выбрана в виде:

N f ( p )=Е y* - у4            (4)

i = 1

В качестве эталонной модели АСЭМ исполь- зовала передаточную функцию

W ( 5 ) =

0.0001 5 ² + 0.02 5 + 1"

При вычислительном эксперименте в среде Simulink MatLab рассматривалось скачкообразное изменение нагрузки (рис. 5).

На рис. 6 показаны активационные функции ИНС (рис. 2) после генетической оптимизации.

Как показал эксперимент, наилучшим постоянным коэффициентом адаптации является Y = 0,5. На рис. 6 и 7 приведено сравнение работы АСЭМ с постоянным коэффициентом адаптации (пунктир) и АСЭМ с переменным у , управляемым обученной ИНС.

На рис. 8 приведен график изменения у во время переходного процесса.

Полученный закон изменения коэффициента адаптации близок к релейному, что обеспечивает высокую скорость протекания переходных процессов.

где у и у * - реальное и желаемое значение выхода объекта, i - момент времени.