Адаптивное управление миллиметровым и субмиллиметровым излучением

Диапазон длин волн от 100 мкм до 5 мм занимает промежуточное положение между хорошо освоенными в оптике ИК диапазоном и диапазоном СВЧ. В настоящее время указанный диапазон начинает интенсивно осваиваться как с помощью оптических, так и радиотехнических методов. Цели, с которыми происходит его освоение, на сегодняшний день могут быть сформулированы следующим образом:

• 1.    Связь и обработка информации. Освоение этого диапазона позволит поднять скорость передачи информации на 2-3 порядка.

• 2.    Локация. Уменьшение длины волны дает возможность повышения разрешения и направленности.

• 3.    Спектроскопия. Диапазону 0,1-5 мм соответствуют частоты, характеризующие мелкие примеси в полупроводниках, обертоны собственных колебаний кристаллической решетки и вращательные частоты молекул.

• 5.    Нелинейная оптика субмиллиметрового и миллиметрового диапазона.

^. Субмиллиметровая лазерная техника.

Для указанных целей необходимо создание отсутствующих в настоящее время элементов управления излучением как традиционного типа, так и управляемых (адаптивных). Элементы управления должны осуществлять модуляцию, сканирование и аподизацию (амплитудную и фазовую) излучения этого диапазона.

В этой связи наиболее перспективными представляются устройства, работа которых основана на свойствах полупроводниковой плазмы, то есть газа свободных носителей в полупроводнике. Отличия полупроводниковой плазмы от более привычной газовой плазмы заключаются в том, что полупроводниковая плазма имеет четкие границы, совпадающие с границами полупроводника, стабильна и обладает более высокой концентрацией. Основным моментом является то, что оптические характеристики полупроводниковой плазмы могут легко изменяться с помощью внешних воздействий. При этом взаимодействие излучения со свободными носителями является доминирующим именно в области миллиметровых и субмиллиметровых волн [1,2].

Оптические характеристики при взаимодействии со свободными носителями определяются временем релаксации по импульсу т и плазменной частотой co p

^ 4nNe ₁{ m* Е

так как

[ф

действительная и мнимая части диэлектрической проницаемости имеют вид

е2 = ----Е (--------), со ы2т2+1

где

Е^ - диэлектрическая проницаемость решетки;

N - концентрация носителей;

со - частота излучения;

т* - эффективная масса; е - заряд.

В (1) входят параметры плазмы N, т, которые могут варьироваться внешними воздействиями. Рассмотрим возможности их изменения.

Время релаксации т определяется многообразными механизмами взаимодействия носителей с нерегулярностями решетки. Основными параметрами, определяющими количественные характеристики этого взаимодействия, являются температура решетки Т совпадающая с температурой в обычном смысле, и энергия носителей 6. Средняя энергия носителей ^Ср может быть определена как температура носителей Т^.

Укажем основные механизмы взаимодействия носителей с решеткой, характерные для полупроводников различного типа [3]:

• -    рассеяние на ионизированных примесях. Этот вид рассеяния является доминирующим при низких температурах и характерен для полупроводников всех типов;

• -    рассеяние на акустических фотонах, также характерное для всех типов полупроводников ;

• -    рассеяние на неполярных оптических фононах. Такое рассеяние возникает в полупроводниках с ковалентной связью с двумя и более атомами в элементарной ячейке;

• -    рассеяние на полярных оптических фононах. Этот вид рассеяния возникает в

гетерополярных кристаллах с ионной связью;

• -    рассеяние на пьезоакус гических фононах. Такое рассеяние характерно для кристаллов без центра симметрии.

• 8 приближении малого отклонения подсистемы носителей тока от равновесного состояния зависимость времени релаксации от температуры решетки Т и носителей Т_± может быть записана в виде

Т р

т(Т,Т. ) = А-ТЧ(—) .                                                          (1а)

• ¹           Т

Значения величин q, р для различных механизмов рассеяния приведены в таблице

Механизм рассеяния	! Ч	! Р
Акустические фононы	1 " 7	1 " 7
Неполярные оптические	3	1
фононы (kT » hw*)	2	" 2
Полярные оптические	3	1
фононы (kT » hcoQ)	" 7	7
Пьезоакустические	__£	1 2
фононы	2
Ионизированные при-	3	3
меси	2	2

* hw0 - дебаевская температура.

При температуре, много ниже дебаевской, рассеяние на оптических фононах не зависит от температуры носителей. Из формулы (1а) и таблицы видно, что наиболее сильная зависимость времени релаксации от температуры носителей наблюдается для рассеяния на ионах примеси. Известно [М], что такое рассеяние доминирует в диапазоне температур 10-100 К, вследствие чего время релаксации изменяется более чем на порядок.

При более высоких температурах доминирующими становятся другие механизмы рассеяния, характеризуемые более слабой зависимостью времени релаксации от температуры носителей. Повышение же температуры носителей выше дебаевской является нецелесообразным, так как при этом происходит быстрая передача энергии решеточной подсистеме.

Коэффициент пропускания излучения определяется величиной мнимой части диэлектрической проницаемости е3. Коэффициенты отражения, определяемые е1 , е2 и формулами

имеют вид:

"V1

cos2 а + а2

2      , 2

cos а + а

2а cos a cos 0

+ 2а cos a cos 0

I «pl1

COS2

а] + 2a2 cos 20 cos2

cos

2 cos 20 cos

а + а2 - А2

а + а2 + А2

А

2а cos a cos S (а2 + sin2 а)

а

X

1+у

sin

х2у2

Е

cos

X²        , 2

у - sin a2

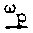
У

(сот) '

угол

падения.

На рисунках 1 - U приведены результаты расчетов

коэффициентов отражения и (плазменной частоты, времени релаксации, угла падения). Из приведенных результатов видно, что при изменении температуры носителей и их концентрации (значением которой определяется плазменная частота) коэффициенты отражения и пропускания изменяются в несколько раз.

пропускания

в зависимости от различных параметров

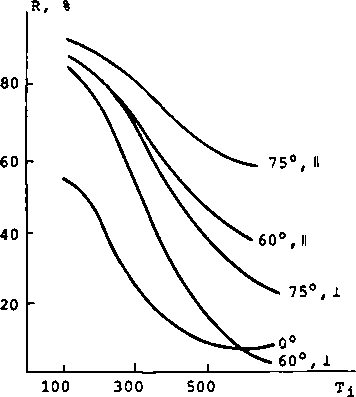
Рис. 1. Зависимости коэффициента отражения от температуры носителей для nGaAs, плазменной частоты top = 5 * 10¹² Гц и длины волны падающего излучения X = 0,376 мкм.

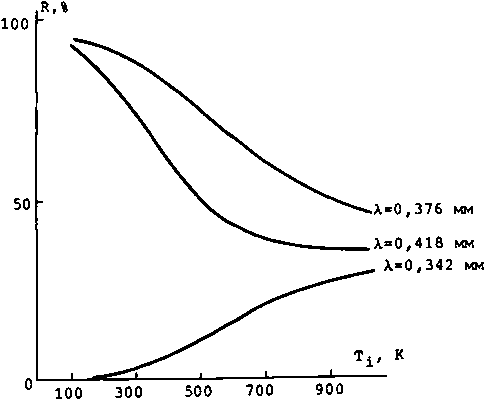
Рис. 2. Зависимости коэффициента отражения от температуры носителей для nGaAs (сор = 5-10¹² Гц) для различных значений длины волны 1 - поляризованного излучения

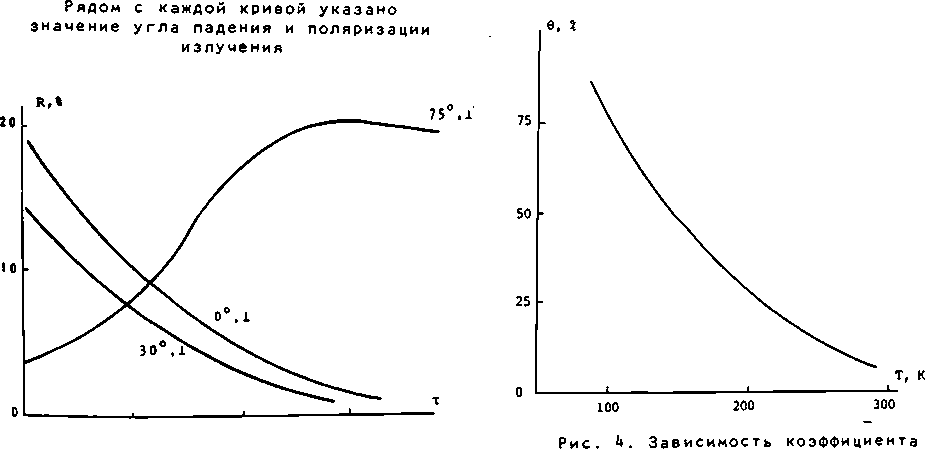
Рис. 3. Зависимость коэффициента отражения от подвижности при разных углах падения пропускания от температуры носителей для nGaAs (N = 2,5•1015 см-3)

толщина 35 мкм, X = 1,^ мм

Концентрация носителей обусловлена уровнем легирования полупроводника, его температурой и скоростью генерации электронно-дырочных пар, вследствие чего концентрация определяется интенсивностью оптического облучения и зависит от характеристик полупроводника. Кинетика населенности в пренебрежении диффузий определяется уравнением [5]

dAN „ AN

"dt" = G "

где

AN - дополнительная концентрация, обусловленная облучением;

G =    - скорость

генерации;

о — поглощение;

I - интенсивность;

т - обратная вероятность рекомбинации; п hv - энергия кванта.

Пои т = 10-6 с. I = Ю'3 Вт/см2, о = Ю3 см-1 AN составляет 1 0 1 “ см-3. Такому п знамению отвечает плазменная частота, соответствующая длине волны 200 мкм. Таким образом, относительно слабая подсветка приводит к изменению плазменной части в широком диапазоне. С учетом пространственного распределения интенсивности I(г) таким путем может производиться амплитудная и фазовая модуляция излучения. Наиболее сильная зависимость коэффициента отражения от температуры носителей наблюдается в том случае, когда значение плазменной частоты, частоты столкновения Т~1 и частоты волны близки. Подсветка полупроводника оптическим излучением позволяет варьировать значение плазменной частоты, а изменение температуры решетки дает возможность управлять исходным значением частоты столкновений.

Характер отражения излучения при взаимодействии со свободными носителями зависит также от магнитиого поля, в котором находится полупроводник. При этом при ориентации поля Н в плоскости полупроводника показатель преломления для обыкновенной волны совпадает с показателем преломления для изотропной среды, а показатель преломления для необыкновенной волны равен

(п - lx)» = | U-p)²-u -,s² -_2is(J-0) I [ 1 - u - 0 - s + is(2-0)   ]

откуда, в случае плазменного резонанса (0=1) , сдвиг фазы при отражении равен

I                   А

6 = т arccos —^^— , /Аа+В2

где e^tu+s2)2          е^ s(u+s2)

(u+s2)2 + s        (u+s2)2 + x2

Таким образом величина сдвига фазы зависит от величины магнитного поля. Это дает возможность осуществлять управление направлением отраженного электромагнитного излучения, то есть его сканирования. При неоднородном распределении магнитного поля сдвиг фаз является функцией пространственных координат, что дает возможность управления кривизной волнового фронта, осуществляя тем самым фокусировку излучения.

Принципиально важным вопросом является вопрос о тепловом режиме полупроводниковых элементов управления излучением. Очевидно, что разогрев носителей в конечном итоге приводит к разогреву решетки вследствие диссипации их энергии. Поэтому длительность пачки управляющих импульсов должна быть достаточно мала, поскольку за время ее прохождения температура решетки не должна изменяться настолько, чтобы привести к заметному изменению оптических характеристик. Кроме того, интервал между пачками импульсов должен быть достаточно велик для того, чтобы температура полупроводника к моменту прохождения следующей пачки достигла значения, близкого к начальному.

Предельная длительность пачки tQ определяется очевидным соотношением t0RIac"’x< | , где

R - сопротивление полупроводника;

с - его теплоемкость;

I - ток, вызывающий повышение энергии носителей на величину 6;

к — постоянная Больцмана.

Расчет величины минимального интервала между пачками требует учета теплообмена с окружающей средой (термостатом).

Пусть температура термостата равна нулю; в соответствии с этим тепловой поток пропорционален температуре границы полупроводника и коэффициенту теплообмена а:

х|1^| -х|^| -атм,.,:).

Решение задачи теплопроводности

9T(x,t) _   32T(x,t)

~--а —- с граничным условием (2) имеет вид:

„ Un ехр(-ц Fo)             R

T(x,Fo) = Е ---—--------:---- COS Ц F / Т X COS U „ dx,                (3)

п_| 1^ * COS U^ sin 1^        n R о н          n R где a = — - температуропроводность; ср

Л - теплопроводность;

с - теплоемкость;

р - плотность;

FO =    * критерий Фурье;

R

Bi = ^5 - критерий Био;

ц^ - n-й корень уравнения Bi " ctg ц = u;

Т (х) - начальная температура.

При периодическом с периодом Fo, воздействии на полупроводник начальная температура равна сумме

Тн (х) = Т, (х) + То (х) , где

Т,(х) - температура к моменту начала пачки;

Т (х) - температура к моменту ее окончания, н

Очевидно, что в установившемся режиме

Т(х, Fo,) = Т, (х)

и уравнение (3) приобретает вид

Т,(х, Fo,)

u ехр(-ц Fo ) Е --------------—:---- COS U р п=1 % + COS un Sin un n R

x / (T,(x, Fo,) + T0(x))cos un £ dx.

Задача свелась к решению интегрального уравнения (4) относительно Т (х, Fo ).

После интегрирования обеих частей (1>) , умножая на cos и § , вследствие ортого-Х                         n R нальности системы функций (cos un ^) получим коэффициенты разложения T,(x,Fo,) по этой системе:

r                            exp(~u Fo,) R               _x

/ T,(x,Fo,)cos un 5 dx = i-exp(-unFo,r {, T°(x) COS Un R dx

Отсюда, проведя обратное преобразование, получим выражение, связывающее установившееся распределение температуры с температурой после воздействия одной пачки:

„ 2sin uR

T^x.FoJ = ^^ ц~+ ^ ц-со- ~- Г To(x)cos цп й dx х exp(-unFOl)          x(

1 - expC-^Fo,) cos WnR'

При равномерном по объему тепловыделении TQ(х) = Т = const формула (5) приобретает вид

Т,(х, FoJ = Т Е A (exp(unFo1) - 1}-1 cos u £ .(6)

При достаточно хорошем теплообмене всеми членами ряда (6), кроме первого, можно пренебречь.

Средняя по сечению температура равна , R                    То А1 sin и

^TCP^(F°1> = R ' VW^ = Ujexpb, FoJ -ТГ '

2sin u

Д — __________2______ n u + sin u cos u n         n n

Условия достаточного остывания можно записать в виде

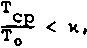
где х - порядок малости.

Для х = 0, 1 это условие приводит к критерию UiXti . „ .

• 8 заключение приведем численные оценки. Амплитуда тока, необходимого для заметной модуляции коэффициента отражения при разогреве носителей, составляет для InSb величину порядка 10 А; величина соответствующего магнитного поля - порядка 200 3. Время t (предельная длительность пачки) для полупроводника толщиной порядка 100 мкм составляет порядка 500 мкс, интервал между импульсами -порядка 2-3 мс.