Адаптивные алгоритмы быстрого поиска многоуровневых шумоподобных сигналов

В работе получены варианты адаптивных алгоритмов быстрого поиска многоуровневых шумоподобных сигналов (ШПС), сформированных на основе многозначных линейных рекуррентных последовательностей максимального периода (МЛРП). Проведен анализ времени поиска ШПС.

Постановка задачи

Системы связи с кодовым разделением, использующие для передачи информации шумоподобные сигналы, содержат в своем составе приемное устройство (ПУ), осуществляющее поиск и синхронизацию с искомой последовательностью. Для обеспечения высокой конфиденциальности передачи сообщений в таких системах применяют бинарные ШПС большого периода, что усложняет реализацию приемных устройств, основанных на классических методах корреляционного поиска или поиска на основе согласованных фильтров [1].

Использование в системах связи МЛРП с основаниями q > 2 позволяет существенно увеличить ансамбль кодовых последовательностей по сравнению с двоичными МЛРП и усложнить распознавание правила формирования ПСП в ШПС, повысив тем самым конфиденциальность адресных систем связи.

Будем полагать, что на входе ПУ в каждом такте работы системы k = 1,2... на интервале T = t (k + i) ^_ t (k) наблюдается аддитивная смесь сигнала и шума x ( t ) = s (^ _k ) + n ( t ) , где s (^_k) - элементарный радиоимпульс ШПС, дискретный параметр которого μ_k (манипулированная частота, фаза и т.д.) в соответствии с правилом кодирования МЛРП, принима ю щей одно из q возможных значений M i , i = 1, q ; n ( t ) — реализация белого гауссовского шума с нулевым средним и дисперсией σ ² _n . Известно, что МЛРП представляет собой сложную детерминированную цепь Маркова [3].

Используя теорию условных марковских процессов требуется разработать адаптивные алгоритмы быстрого поиска ШПС, сформированных на основе многозначных МЛРП с основанием q≥ 2 .

Уравнения фильтрации дискретного параметра ШПС

Символы МЛР a _k с произвольным числом значений q формируются в соответствии с рекуррентным правилом кодирования [1]:

m

ak =1Z cak- I mod q,

V i = 1          )

где c _i ( i = 1... m ) – целочисленные коэффициенты, k – номер такта. В МЛРП последовательность m -значных комбинаций можно интерпретиро ва ть как цепь Маркова с q значениями M i ( i = 1, q ) и вероятностями перехода между значениями принимаемого в ( k + 1)-м такте работы системы ^ k _{+ 1} = M. и сформированного в k-ом такте ^j

^ k = ^M i :

^п и = ⁿ ( ^ + i = M j |n k = M i ) , i , j = i, q .

При отсутствии шума ^ _{k + 1} = ^ _k .

Учитывая, что μ _k+1 и μ _k формируются по одному правилу и образуют q- значную детерминированную цепь Маркова уравнение для апостериорной плотности вероятности pa + 1 ( ц _{к + 1} ) значений дискретного параметра искомого ШПС в ( k + 1)-м такте можно записать в виде [3]:

P a + 1 ( H k + i ) = ^{c X} exp { ^f ( H k + i ) } ^{X X} J P a ( h k ) w ( H k + 1 |h k ) d H k ,

где

c - коэффициент нормировки, f ( ^ k + 1 )

– логарифм функции правдоподобия параметра

^ k + 1 ,     w ( H k + 1 |n k )

– плотность вероятности пе- ^

рехода из значения μ _k в k-ом такте в μ _k+1 на ( k + 1)-м такте.

Представим в (2) апостериорные плотности вероятности и плотность вероятности перехода в виде:

q

Pk (Hk) = Zp^k)8 (Hk - Mi),

q pac+i (^k+1) = ZpJ(k+1)8(^k+1 - Mj), j=i

w(^k+1 |hk) = Znj8 (Hk+1 - Mj), j=1

где Р^к ) , ^p j ( k + 1 ) — апостериорные вероятности значений параметров ^ _k в k -м такте и ^ _{k + 1} в ( к +1)-м такте соответственно; 8 ( • ) -дельтафункция.

Подставив уравнения (3)-(5) в (2), проинтегрировав и приравняв коэффициенты при одинаковых дельта функциях, получим систему рекуррентных уравнений для финальной апостериорной вероятности дискретного параметра ШПС:

q

Р j ( k + 1 ) = c ^х exP { f k + i ( M j )} E P (k ) ^п и ,     (6)

= 1

где j = й; fk+1 (Mj) = f (^+1 = Mj).

Уравнения (6) являются основой для синтеза приемных устройств фильтрации ШПС, построенных на МЛРП с произвольным основанием.

Синтез приемного устройства ШПС

Для удобства различения значений дискретного параметра переведем уравнения (6) в аддитивную форму. Для этого разделим каждое j-e уравнение в (6) на последнее ( j = q ) уравнение и, прологарифмировав обе части результата, получим:

u1( k + 1) = [ fk + 1 ( M1 ) — ft + 1 ( Mq )] + 'll 1(k) + z1(k), u j(k + 1) = [ fk + 1 (Mj ) — fk + 1 ( Mq )] + u j(k) + zj(k) , канала нелинейного фильтра формируется следующим образом [4]:

|uv ( k)| ,   ^ k = M j ,

u j(k) =<0, Цk * Mj , Цk * Mq,      (9)

— |uv(k)| , П, = Mq ,

где j = 1,(q -1),

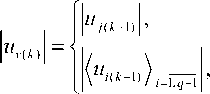
μ _k =M _j ,

(10) μ _k =M _q ,

⋅ – операция усреднения.

В частном случае вырожденной цепи Маркова, когда n i = 1 , функция z д_к ) = 0 и система уравнений (7) принимает вид:

u 1( k + 1) = [ ^fk + 1 ( ^M 1 ) — ^fk + 1 ( ^Mq ) ] ⁺ uKk ) ,

u2(k+1) = Гf t+1 (M2 ) — f t+1 (Mq )-| + u2(k),

u(q-1)(k+1) = Гfk+1 (M(q-1) ) — f t+1 ( Mq )] + uj(k) ’ то есть осуществляется «чистое» накопление ШПС.

Примем в качестве критерия различения значений дискретного параметра ^k+1 = {M1,...,Mq} критерий максимума логарифма отношения апос териорных вероятностей uj(k+1), j = 1,(q -1):

u ( q - 1\ k + 1) = [ ^fk + 1 ^{( M} ( q - 1) )   ^fk + 1 ^{( M} q ^ ⁺

^k+1 = 1

[ M v ,

A

^{+ u} (-Hx k ) ^{+ z} ( q - 1)( k ) ,

где j = 1,(q -1),

q ^{- 1}

E {exp( i=1,i*

A

A

U i (k )     U j ( k )

+

z j ( k ) = ln

qq

( A

^U j( k ) ) + ⁿ jj

x4         \ I

EjexP (Ui(k) ) niq } + % i=1

^M q ,

u v(k + 1)

u v(k + 1)

где u v ( k +1) = max { u 1( k +1) ,

< °’ (12)

.., u v ( k +1) ..., ^u ( q —1)( k +1) ^{} ;}

ин-

декс v = 1,(q -1) относится к каналу выделения дискретного параметра ^ k + 1 ■

В качестве критерия обнаружения искомого ШПС примем критерий Неймана-Пирсона [2],

в соответствии с которым решение о наличии, либо отсутствии сигнала выносится на основании сравнения накопленного сигнала на выходе ПУ |u _v (k)| с порогом h :

| uv (к )| ^ h ,

где uj(k + 1) = ln ( Pj(k +1)/Pq(.k + 1) ) - логарифм отношения апостериорных вероятностей значений дискретного параметра ^k+1, uj(k) - оценка напряжения uj(k+1) в k-м такте, которая при отсутствии шума совпадает с uj(k+1). Оценка u jk) для j-го где h определяется, исходя из заданной вероятности ложной тревоги а.

При условии, что элементы МВП заданы следующим образом:

^п _м = ( 1 ^-п н Жq ^- 1 ) , (i * j ); i , j = i, q , (14)

тогда с учетом (14) и (9) выражение (8) после некоторых преобразований можно представить в более кратком виде [4]:

z _{j ( k} ) = sign ( u j (k ) ) ^x

~ in

Пи( к + 1) = <

ⁿ ii (k ) + Aⁿ ii ,

2 ^пй( k )

A

^- Aⁿ ii ,

×ln

π _ii +π _ij

π _ii +π _ij

где sign ( u j(k ) ) -

,i≠j ,

a out

Пи( к + 1) = *

Пи ( k ) + АП- ,

A

Пи ( k )

- Δπ _ii ,

Z^ in __ _H , ^ k + 1 = ^ k ;

, in

^ k + 1 ^ ^ k •

A

^ k + 1 = ^ k

A ,

^ k + 1 ^ ^ k

где

Пн ( k ) - оценка значений

диагональных

эле-

знак, вычисляемый согласно

ментов МВП на k -ом такте, Δπ _ii – шаг адаптации. Значения элементов МВП π ij ограничены диапа-

условию (9); значение гласно (10).

|u v(k)| формируется со-

зоном П и мировки

е [ 1 q ;1 ] и удовлетворяют условию нор-

Рассмотрим комбинированный алгоритм адаптации, основанный на работе алгоритмов адаптации по выходу и по входу. Алгоритм комбинированной адаптации описывается уравнением

q

^ n ij = 1; i , j e Z; i = 1, q .

j =1

i = const

2 in

Пн ( к + 1) = <

n a^k ) , V l >  K ; l = ( k - K + 1), k : n_U ( i ) = 1

₂ out                                               ,⁽¹⁶⁾

П н ( к )

где K – порог переключения (в тактах) c адаптации по выходу на адаптацию по входу;

in            out

Пп( к ) и Пн( k )

–

оценки значений элементов

МВП, полученные в случае работы алгоритма адаптации по входу (17) и алгоритма адаптации по выходу (18) соответственно

Обобщенная структура модифицированного ПУ быстрого поиска с комбинированной адаптацией, реализующая алгоритм (7) с нелинейной функцией (15) и алгоритм адаптации (16), представлена на рис. 1.

Устройство состоит из дискриминатора (Д) с ( q – 1) выходами, формирующего разности логарифмов функций правдоподобия f ( ^M j ) — f ( ^M q ) ; многоканального нелинейного фильтра с ( q – 1) каналами; блока вычисле-

ния

нелинейной функции (БНФ) z (| u _{v ( к} ) | , п у ( к ) ) ;

;

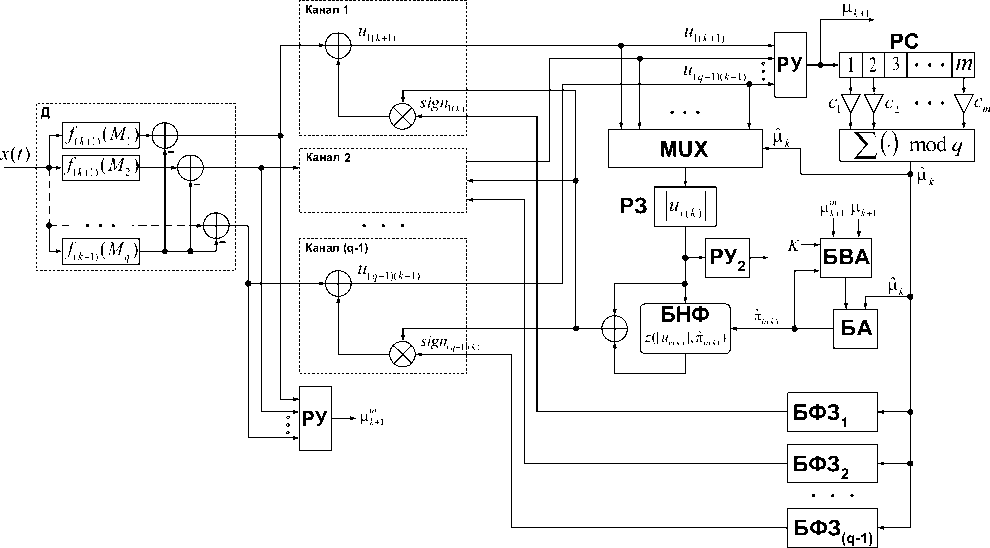
Рис. 1. Обобщенная структура модифицированного ПУ с комбинированной адаптацией

сумматора; регистра задержки (РЗ) на такт для хранения модуля |u _{v (k} J; сумматоров ( ® ); и умножителей ( ® ); решающего устройства (РУ) для различения значений МЛРП в соответствии с (12), и аналогичного РУ на входе НФ; регистра сдвига (РС) m -значной комбинации символов ПСП; мультиплексора (MUX) для формирования |u _v(k)| ; блоков формирования знаков (БФЗ) значения |u _{v (k})| ; решающего устройства (РУ 2 ), определяющего наличие, либо отсутствие ШПС в соответствии с (13); блока адаптации (БА); блока выбора адаптации (БВА).

В случае ПУ с адаптацией по входу структура ПУ (рис. 1) отличается отсутствием блока БВА, а изменение МВП производится блоком БА на основании сравнения оценки |д _k c ц к согласно (17). В случае ПУ с адаптацией по выходу структура ПУ (рис. 1) отличается отсутствием блока БВА и блока РУ на входе нелинейного фильтра (НФ), а изменение МВП производится блоком БА на основании сравнения оценки ^ _k c ^ _k + 1 согласно (18).

Входными параметрами блока БВА являются значения дискретных параметров ^" + 1 и ^ _{k + 1} , полученные со входа и выхода НФ соответственно, а также значения оценки п щк ) и порога переключения K с адаптации по выходу на адаптацию по входу. Параметр K ≥ 0 задается априорно. Блок БВА согласно алгоритму (16) определяет моменты времени поочередной работы алгоритма адаптации по выходу и алгоритма адаптации по входу.

В отличие от структуры ПУ, реализуемой с помощью уравнений фильтрации (7)-(9) и имеющий в своем состав ( q – 1) блоков БНФ (8), в модифицированном ПУ (рис. 1) присутствует единственный более простой блок БНФ, описываемый уравнением (15).

Анализ времени поиска ШПС

При решении задачи одновременного обнаружения и распознавания (поиск) ШПС приемным устройством (рис. 1), возможны ошибки следующего вида [2].

Ошибка ложной тревоги ( α ) возникает при принятии решения о наличии ШПС, когда искомый сигнал на входе ПУ отсутствует. Ошибка пропуска ШПС ( ß ) возникает при принятии решения об отсутствии ШПС, когда искомый сигнал присутствует на входе ПУ. Ошибка искажения ШПС ( γ ) возникает при неправильном распознавании ШПС в случае его обнаружения.

Введем вероятность правильного одновременного обнаружения и распознавания m -значных комбинаций МЛРП d :

d = ( 1 “Y )( 1 -а) . (20)

На рис. 2-3 приведены зависимости вероятности правильного одновременного обнаружения и распознавания m -значных комбинаций МЛРП d искомого ШПС от времени поиска ШПС T _ПОИСКА при заданной вероятности ложной тревоги α для трех алгоритмов адаптивной нелинейной фильтрации: АНФ(вх) – с адаптацией по входу, АНФ(вых) – с адаптацией по выходу и АНФ(комб20) – с комбинированной адаптацией при пороге переключения K = 20 тактов.

Анализ времени поиска проводился для двух случаев: рис. 2 соответствует случаю, когда искомый сигнал появляется на входе ПУ на k _СИГ = 1 такте с момента начала фильтрации ШПС ( к _сИГ – номер такта фильтрации, на котором появился искомый ШПС на входе ПУ); рис. 3 соответствует случаю, когда искомый сигнал появляется на входе ПУ только с k _СИГ = 201 такта с момента начала фильтрации ШПС (до 200-го такта сигнал на входе ПУ отсутствует). Результаты анализа приведены при заданном отношении сигнал/шум (по мощности) на входе ПУ при р Э = 0 дБ и вероятностях ложной тревоги а = 0,01 (сплошная линия) и α = 0, 001 (пунктирная линия). Правило кодирования МЛРП ШПС для всех случаев при q = 7, m = 3: a k = (5 a_k -1 + 3 a_{k - 2} + 5 a k _{- 3} ) mod 7 .

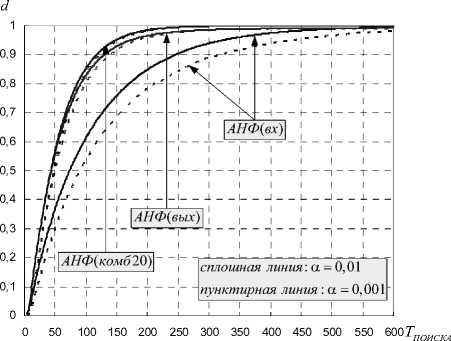
Рис. 2. Время поиска ШПС при k _СИГ = 1 .

Как видно из рис. 2-3, с увеличением времени появления сигнала кСИГ скорость роста вероятности d на начальных тактах с момента появления сигнала на входе ПУ уменьшается. Чем больше время поиска ШПС, тем выше вероятность правильного обнаружения, но при этом снижается скорость поиска ШПС.

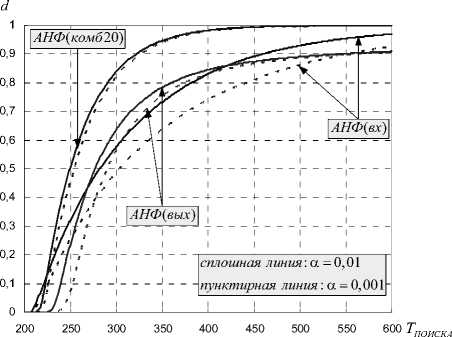
Рис. 3. Время поиска ШПС при k _СИГ = 201

Для примера определим вероятность правильного одновременного обнаружения и распознавания m -значных комбинаций МЛРП d для приведенных результатов (рис. 2-3) при следующих заданных условиях: МЛРП с параметрами q = 7, m = 7 и периодом L = q ^m -1 = 7 3 -1 = 342 символа; отношение сигнал/шум (по мощности) р Э = 0 дБ ; вероятность ложной тревоги α = 0, 001 ; время поиска ШПС T _ПОИСКА =300 (где T _ПОИСКА для обеспечения условия быстрого поиска ШПС за интервал времени меньший длительности периода МЛРП).

В условиях примера вероятность того, что искомый ШПС будет обнаружен и правильно распознана m-значная комбинация МЛРП равна d=0,99814 (рис. 2) и d=0,81924 (рис. 3) в случае алгоритма с комбинированной адаптацией АНФ ( комб20 ); в случае алгоритмов с адаптацией по входу ( АНФ ( вх )) и выходу ( АНФ ( вых )) вероятность d на интервале поиска T _ПОИСКА гораздо меньше: для АНФ ( вх ) вероятность d = 0,88933 (рис. 2) и d = 0,48561 (рис. 3); для АНФ(вых) вероятность d = 0,98415 (рис. 2) и d = 0,56102 (рис. 3). С увеличением времени появления сигнала ( k _СИГ = 201 ) относительно момента времени начала фильтрации вероятность d резко снижается для алгоритмов адаптации по входу и по выходу (см. рис. 3).

Таким образом, в условиях рассмотренного примера ПУ с комбинированной адаптацией (рис. 1) обеспечивает быстрый поиск искомого ШПС с более высокой вероятностью правильного одновременного обнаружения и распознавания d (в сравнении с алгоритмами адаптации по входу и по выходу) за время T _ПОИСКА , не превышающее длительности периода МЛРП L .

Выводы

Как видно из рис. 2, при известном моменте появления сигнала ( k _СИГ = 1 ) самая низкая вероятность правильного обнаружения и распознавания m -значных комбинаций МЛРП свойственна для алгоритма с адаптацией по входу, самая высокая – для алгоритмов с комбинированной адаптацией и адаптацией по выходу.

При неизвестном моменте появления сигнала (рис. 3) (например, сигнал появился на входе ПУ при k _СИГ = 201 ) вероятность d будет наибольшей для алгоритма с комбинированной адаптацией и наименьшей – для алгоритмов с адаптацией по выходу и входу.

Результаты анализа показывают (рис. 2, 3), что в случае алгоритма с комбинированной адаптацией вероятность правильного обнаружения d практически не снижается при изменении вероятности ложной тревоги α от 0,1 до 0,001 при различных моментах времени появления сигнала k _СИГ на входе ПУ; тогда как в случае алгоритма адаптации по выходу и, особенно, алгоритма адаптации по входу разница в изменении вероятности d при изменении вероятности ложной тревоги α от 0,1 до 0,001 достаточно велика (рис. 3).

Таким образом предложенные алгоритмы адаптивной фильтрации обеспечивают быстрый поиск ШПС за время, не превышающее длительности периода МЛРП в сравнении с известными методами поиска ШПС на корреляторе или согласованными фильтрами, которые при поиске ШПС с большой базой требуют значительных временных или аппаратурных затрат.