Адаптивные системы в коротковолновом диапазоне

АДАПТИВНЫЕ СИСТЕМЫ В КОРОТКОВОЛНОВОМ ДИАПАЗОНЕ

В статье на примере полупроводника n-типа, в частности, inSb и Ge показано, что когда частота падающей волны со, лэнгмюровская частота носителей Q и час-е тота столкновений v-величины одинакового порядка, имеет место существенное возмущение е. Ее действительная и мнимая части (R = Ree и I = Ime) становятся одинакового порядка, что приводит соответственно к возмущению амплитуды IRI и фазы <р отраженных волн. Таким образом, в статье показывается, что имеет место контролируемая тепловая перестройка амплитуды и фазы отраженного волнового пучка при нагреве носителей.

Влияние электронной температуры носителей на амплитуду IR) и фазу ср комплексного коэффициента отражения R^e”^^ удобно представить, разделяя в известных формулах Френеля действительную и мнимую части [ 1] . Результат такого преобразования для S- и р-поляризованных волн, падающих под углом а, имеет вид:

IR |а - cos² g + a² - 2a*cos crcos 8 .

s * cos2 а + а2 + 2а-cos a-cos в 1

j р । 2 - cos² a(a^sin⁴ QiH^a^ sin^{2 a} cos² a cos 26+а²-2а cos a*cos 6(a²+sin² a) , ,₂. ₽     cos² a(a*+sin⁴ a)+2a⁵ sin⁵ a cos⁵ a cos 26+3^+23 cos a cos 8(a²+sin² a) ¹

cos ^s = — ■ '    ---C-S—a —a-----;(3)

/Teos2 a - a2)2 + 4a2 cos2 a-cos2 0

cos m -           cos2 a(a4 + sin4* a) + 2а2 sin2 a cos2 a cos 28 - a2.

Vcos^aTa^-Fsin^a)+2a2sin2a*cos2a*cos 28-a2]2+4a2cos2a sin28 (a2»sin2a)2

J         ~                    e,-V-S a= = y[eL(l - ^) - sin= a]= + [-^=- ]= ;(5)

cos 28 = [eL(l 4n e2 Ne

V = -___________ .

mx co2

- j^j) - sin2 a] - a2 ;

s = m (q+Pf)? Sa. = ^

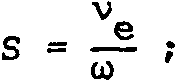
10 рО /о \

^ = Vio+vPo' Ч = ' Р = ' (8) где температурная зависимость представлена через частоты столкновений в безразмерной форме:

S/Ge = so/f? S/InSb = ^ .                                                  (9)

В формулах (1)-(4) интенсивности и фазы отраженных сигналов для S- и Р-по-ляризованных волн представлены через дополнительные коэффициенты (5)-(9) и через частоту столкновения s, зависящую от температуры нагрева носителей f = Т • Т~2 • е ео

Исходя из (1)—(4) и (5)-(8), мы поточечно рассчитаем на ЭВМ зависимость интенсивности и фазы отраженных S- и Р-поляризованных волн от температуры нагрева носителей f, а также от угла падения а (рис. 1) волны на поверхность вышеназванных полупроводников. Полученные графики на рисунках 2, За,б и 4 наглядно демонстрируют возможность контролируемого управления интенсивностью и фазой отраженных сигналов.

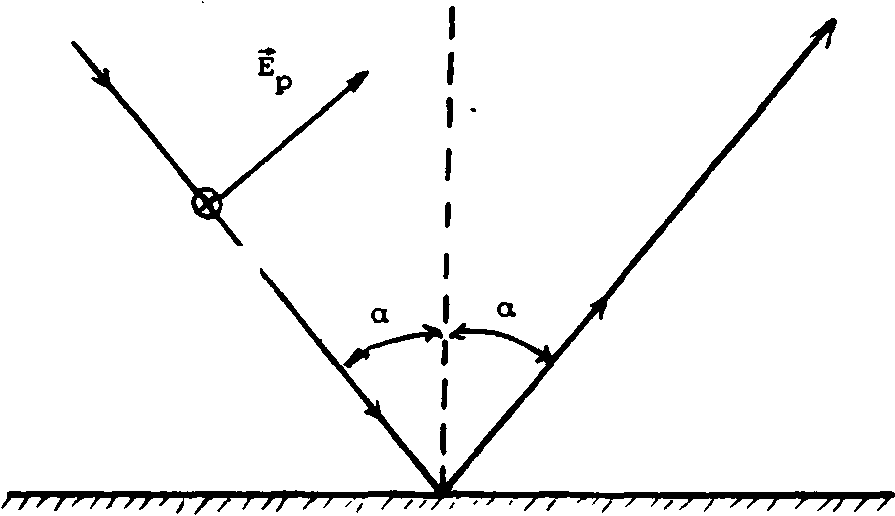
Рис. 1. Геометрия отражения S- и Р-поляризации от полупроводниковой пластины; а - угол падения

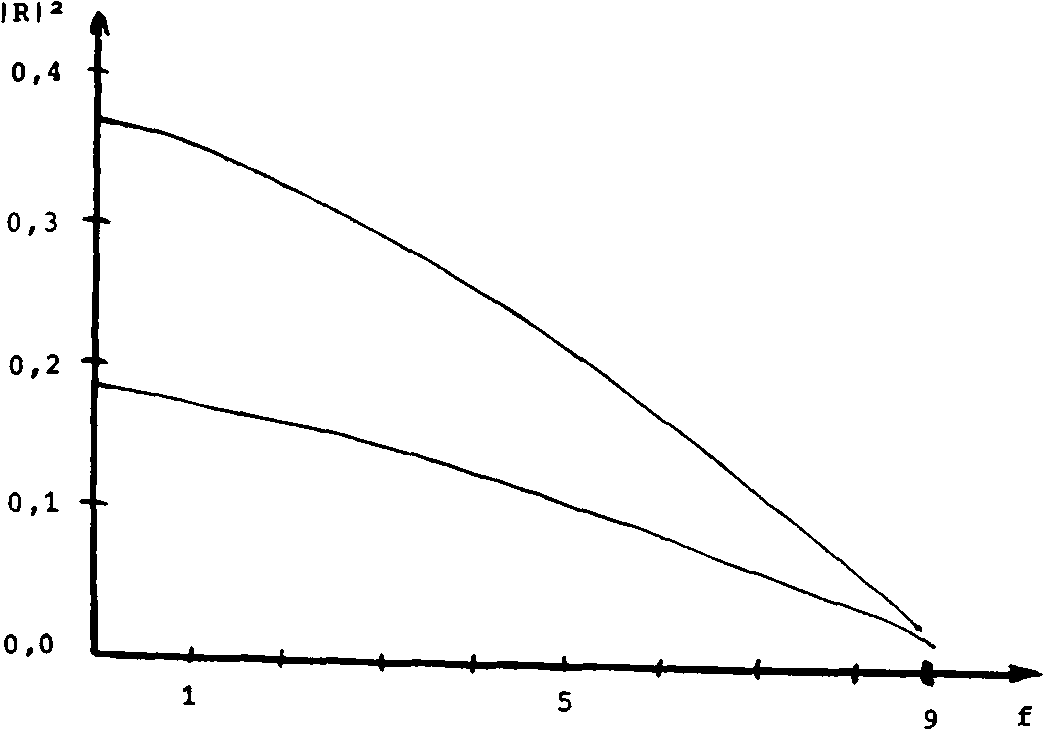
Рис. 2. Зависимость коэффициента отражения волн по интенсивности I RI 2 от температуры носителей f при падении излучения X = 200 мк под углом а=45° на поверхность n-InSb; Т - 78°К; кривые 1 и 2 относятся к S- и Р-поляризации с8ответственно

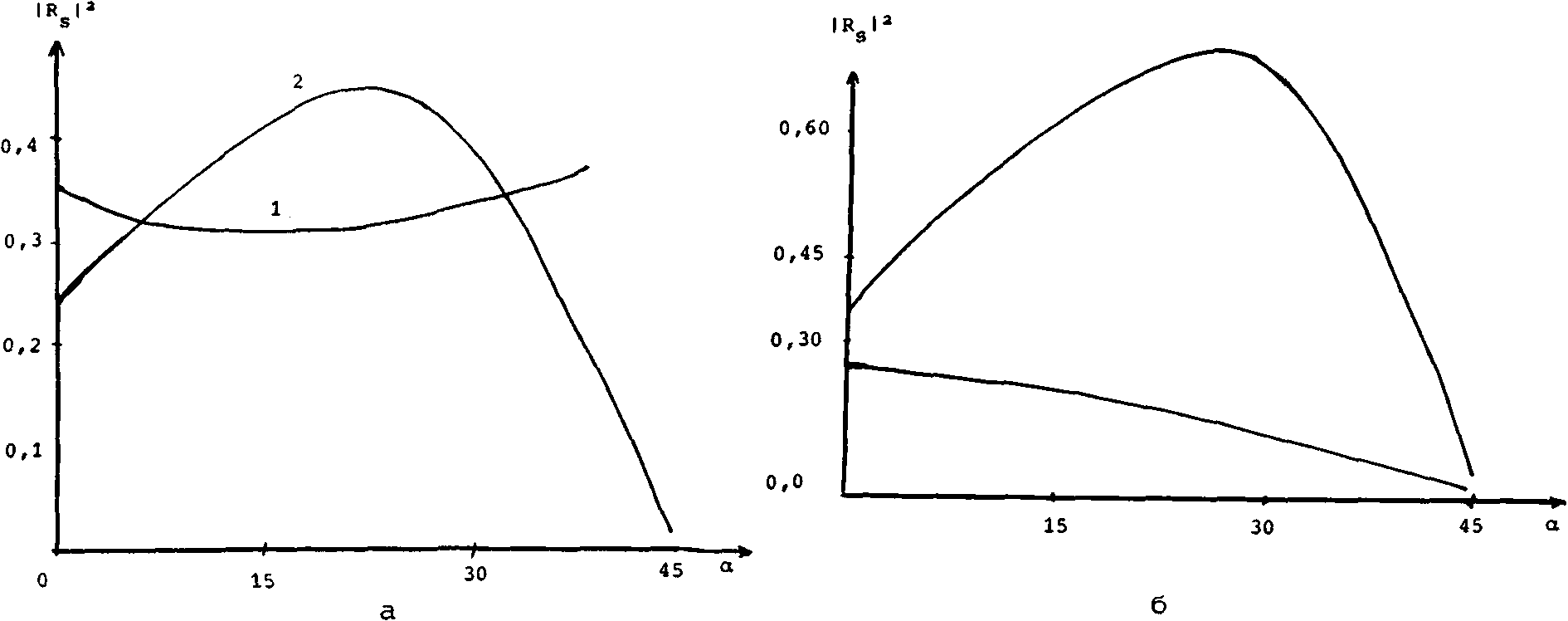
Рис. 3. Зависимость коэффициента отражения по интенсивности излучения X = 200 мк от угла падения на поверхность n-InSb Т = 78°К; кривые 1 и 2 соответствуют температуре носителей ео                       f = 1 и f = 9:

a) S-поляризация; б) Р-поляризация

Ф8

о

9 f

Рис. 4, Температурная зависимость фазы отраженной S-поляризации (f - температура носителей) при падении излучения X = 200 мк, Т = 78°К; кривые 1 и 2 соответствуют углам падения а = 0° и ео                           а = 30°

Так, например, на рис. 3 видно, что в интервале а = 0°-30° тенденции температурного изменения величины IRI2 противоположны для S- и Р-поляризации: интенсивность отраженного сигнала при нагреве электронов падает для S-поляризации и возрастает для Р-поляризации. При дальнейшем росте угла падения (а = 45°) коэффициенты отражения для обеих поляризаций падают до малых значений (см. рис. 2). Температурный ход фазового сдвига для разных углов падения показан на рис. 4. Следует отметить значительную величину температурного сдвига фазы Лф = Фд|£-9~ - ^g|f=i отраженной волны Аф = при нагреве электронов в 9 раз.

Хотелось обратить внимание на релаксацию электронной температуры в рассматриваемых процессах [2,3]. В нашем случае теплового нагрева носителей частота столкновений ^1011т1013 с-1, поэтому средняя доля энергии 5, переданной электрону при одном ударе порядка 10~3 для InSb и 10~2 для Ge. Тогда характерное время установления рассматриваемых процессов или время релаксации электронной температуры тт = (6v)-1 = Ю-^тЮ-11 с. Такие времена установления представляют интерес для создания устройств плазменной электроники.

Таковы теоретические возможности контролируемой перестройки амплитуды, фазы и поляризации волнового пучка в коротковолновом диапазоне, связанных с отражением пучка от слоя полупроводника n-типа при нагреве свободных носителей.