Адаптивный алгоритм фильтрации параметров движения космического объекта на геостационарной орбите

В задачах определения текущего положения космических объектов в пространстве (далее – ТПКО) [5; 12] на основе динамической фильтрации измерений параметров движения основным этапом является обеспечение устойчивости рекуррентного фильтра [4; 7]. Данный этап относится к проблеме решения некорректных задач, а именно, когда небольшие отклонения в исходных данных вызывают сколь угодно большие (но конечные) отклонения в решении.

Для задач данного типа разработан метод устойчивого (приближенного) решения – метод регуляризации. Общий подход состоит в искусственном загрубении результатов измерений, ограничении памяти или расширении полосы фильтра [7; 8; 11].

Такой подход к решению задачи определения ТПКО с учетом особенностей его маневрирования на геостационарной орбите (далее – ГСО) может привести не только к снижению точности оценок параметров движения космического объекта (далее – КО), но и к недостоверной классификации ТПКО (обнаружение маневра и т.п.).

Таким образом, актуальной является разработка адаптивного алгоритма фильтрации параметров движения КО в интересах решения задачи определения ТПКО на ГСО.

Постановка задачи

Совокупность КО и средств измерений (далее – СИ) представляет собой непрерывнодискретную систему, в которой функционирование КО – непрерывная динамическая система, а функционирование СИ – дискретная измерительная система.

Решение задачи оценивания параметров движения КО на ГСО возможно за счет использования расширенного фильтра Калмана для нелинейных динамических систем [1].

Особенностью решения задачи оценивания параметров движения КО является то, что фильтруемые параметры движения представляются в прямоугольной геоцентрической системе координат, а измеряемые параметры движения – в сферической подвижной измерительной системе координат.

Основные соотношения рекуррентного адаптивного фильтра можно представить в следующем виде [1; 6; 7; 14; 15]:

9 к = Fk 9 к-1;(1)

т» k = FY6 к—1FT+Q к-1;    ](2)

Kk = Yjk НТТ(н kYjk Н + R к )"*;(3)

О к = О k + K k (Yk - YЭ);(4)

Yek = Ylk — K kHkYXk,(5)

э где θk – экстраполированные значения оцениваемых параметров движения КО; Fk – матрица экстраполяции оцениваемых параметров движения КО; γθэˆ – экстраполированная ковариационная матрица оценок параметров движения КО; Qk-1 – ковариационная матрица шума процесса функционирования КО; Yk – вектор измеренных значений параметров движения КО; Ykэ – вектор экстраполированных значений измеряемых параметров движения КО; Rk – ковариационная матрица погрешностей измерений; Kk – матричный коэффициент усиления фильтра; γθˆ – ковариационная матрица оценок параметров движения КО.

44 в ыпуск 2/2020

Матрица частных производных H _k представляет собой линеаризованный оператор, устанавливающий связь между измеряемыми и оцениваемыми параметрами движения КО [7].

Стоит отметить, что вектор экстраполированных значений измеряемых параметров движения КО ( Y ^ ) рассчитывается на основе экстраполированных значений оцениваемых параметров движения КО ( § k ) с использованием уравнений связи измеряемых и оцениваемых параметров движения КО.

Необходимо определить способ формирования Q _{k - 1} , обеспечивающий получение несмещенных и эффективных оценок параметров движения КО в интересах решения задачи контроля его состояния.

Решение

Формирование матрицы Q _{k - 1} возможно методом уточнения ковариации на основе принципа согласованности или других методов оперативной коррекции процессов фильтрации [2; 9; 10; 16] путем представления ее в виде оценки Q _{k - 1} .

Однако в задачах определения ТПКО на ГСО такие подходы к построению адаптивного рекуррентного фильтра приводят к погрешностям оценок параметров движения КО и не позволяют получить решение.

Построение матрицы Q _{k - 1} возможно за счет анализа прогноза k – 1 и формирования оценки Q _{k - 1} с использованием модифицированного метода уточнения ковариации на основе выражения [3; 13]:

	σ2 q ˆ1	cov ( <7 1 , . ) •	• cov ( <1 1 , I)
1       к —1                              т ˆ             1           ˆ     ˆэ ˆ     ˆэ	cov ( . . < )	2 a <  2	• cov ( )	, (6)
Q k - 1 = ( k - ^v j ° j )( ° j ° j ) =	cov ( < 1 , <7 1 )	cov ( <7 1 , < < 2 ) •	σ 2 q ˆ I

22    2

где о q1, G q2, ...,G qI - дисперсии оценок шумов q1,q2,...,qI; I - количество оцениваемых параметров движения КО.

Модификация метода уточнения ковариации заключается в следующем.

На каждой итерации формирования оценки Q _{k - 1} проверяется условие

1/2        -----

16 6э| <(^У6к_J , i = 1,1,                       (7)

где σ ² γ _{θ ˆ , i} – элемент главной диагонали матрицы γ _ˆ .

При выполнении условия (7) i -я строка и столбец оценки Q _j обнуляются:

	q ˆ11	q ˆ12	..   0    .	q ˆ1 I
	A q ˆ 21	q 22	0    .	A q ˆ2 I
T , = ( 6 , - 6 Э )( 6 , - 6 Э ) =	0	0	0 .	0	, j e[ 1, ( k - 1 ) ] . (8)
	A qI 1	A q ˆ I 2	0 .	A qII

Жуков А.О., Крупский К.А., Пестун У.А. Адаптивный алгоритм фильтрации...

Учет оценки Q _{k - 1} в уравнении (2) осуществляется с использованием условия (7), при выполнении которого i -я строка и столбец оценки Q _{k - 1} обнуляются:

cov ( q I , q )

cov ( q I , q ₂ ) -

ˆ

Такой подход к формированию оценки Q _{k - 1}

0 -

σ² q_I

позволяет обеспечить сходимость

процесса фильтрации при минимальной дисперсии оценок параметров движения КО.

Основными этапами реализации адаптивного алгоритма фильтрации параметров

σ2qˆ1 cov (Ch, q2 ) • ■    0    - ■ cov (Ch, CjI) cov (q2, qi ) σ2qˆ2 ■    0    - ' cov ( q2, qI ) A

ˆ

Этап 1. Формирование начальных условий k = 1, Q₀= 0.

Этап 2. Аппроксимация шума процесса Q j = ( 0 j — 0э )( 0 j — 0э) , j = k.

Этап 3. Проверка условия (7).

Этап 4. Уточнение шума процесса Q_k с использованием выражения (8). _ˆ

• k — 1 Q j

Этап 5. Формирование оценки Qk - Qk =----Qk- 1 +--- .

Этап 6. Проверка условия (7).

Этап 7. Уточнение оценки Q_k с использованием выражения (9).

Этап 8. Учет оценки Q_k в уравнении (2).

Этап 9. Переход к следующей итерации k+ = 1.

Реализация приведенных выше этапов позволит осуществлять формирование оценки Q_k-1независимо от ее учета в выражении (2).

Расчетный пример

Апробация разработанного алгоритма проводилась при следующих исходных данных:

• •    два КО на ГСО, первый КО – объект контроля, второй КО измеряет наклонную дальность до первого КО (r), его угловые координаты (α, β) и радиальную скорость (Vr) в подвижной измерительной системе координат;

• •    дискретность измерений 10 с;

• •    σr = 0,3 м;

• •    σVr = 0,01 м/с;

• •    σα, σβ = 10 угл. сек;

• •    θˆ _КО= xˆ yˆ zˆ Vˆx Vˆy Vˆz   – вектор оцениваемых параметров движения

КО в геоцентрической системе координат.

Ограничения и допущения:

• •    погрешности измерений распределены по нормальному закону;

• •    измерения имеют равную точность, корреляция отсутствует;

46 выпуск 2/2020

• •    при моделировании движения КО давление солнечного излучения, притяжение пла-

• нет не учитывались;

• •    поле зрения средств измерений КО обеспечивает получение измерений на всем интервале моделирования движения КО.

С учетом особенности маневрирования КО на ГСО (маневрирование осуществляется в плоскости OXY геоцентрической системы координат), основным подходом к решению задачи определения ТПКО на основе динамической фильтрации измерений параметров его движения будет являться контроль оценок составляющих вектора скорости КО на выходе рекуррентного фильтра.

Непрерывно-дискретная система описывается уравнениями вида где τ – дискрет измерений;

9 k = Fk 9 к-1; Yk = H к 0 к + R к. (10) (11) Матрицы Fk и Hk имеют вид 1 0 0 т 0 0 ∂r дг/    .. ∂r ∂x ∂y ∂Vz 0 1 0 0 т 0 ∂α ∂α ∂α F. = 0 0 1 0 0 т , H = ∂x ду ∂Vz ,      (12) k 0 0 0 1 0 0 k ∂β дР/   .. ∂β 1 0 ∂x ∂y ∂Vz 0 0 0 0 ∂Vr д Vr/   .. ∂Vr 1 0 0 0 0 0 ∂x ∂y ∂Vz d r/ ... d Vr/

∂x      ∂Vz

– частные производные от измеряемых параметров по оцениваемым параметрам движения КО.

На рисунках 1–3 представлены функциональные зависимости оценок составляющих

вектора скорости (Vx, Vy, Vz) КО от времени по результатам работы расширенного рекуррентного фильтра, настроенного методом уточнения ковариации, и с использова- нием разработанного алгоритма.

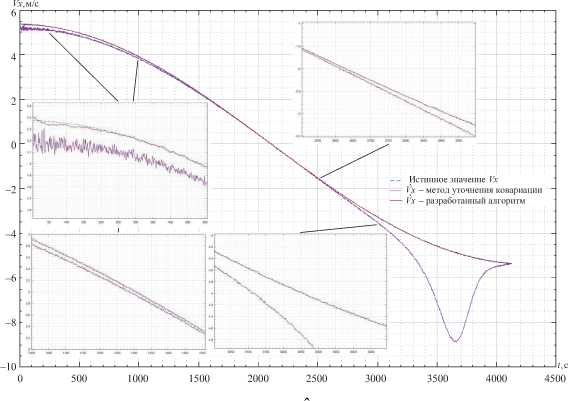
Рис. 1. Функциональные зависимости оценок Vx КО от метода формирования матрицы Q

Жуков А.О., Крупский К.А., Пестун У.А. Адаптивный алгоритм фильтрации... 47

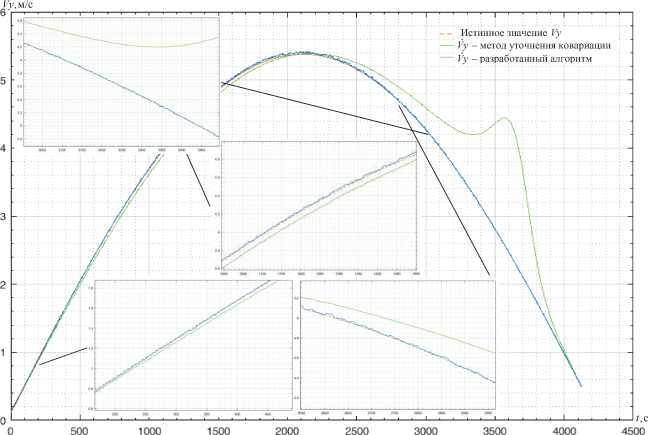
Рис. 2. Функциональные зависимости оценок Vy КО от метода формирования матрицы Q

ˆ

0.07

0.06 г

0.05 к

0 04 Г

0.03 Г

0.02 Н

0.01 b t, с

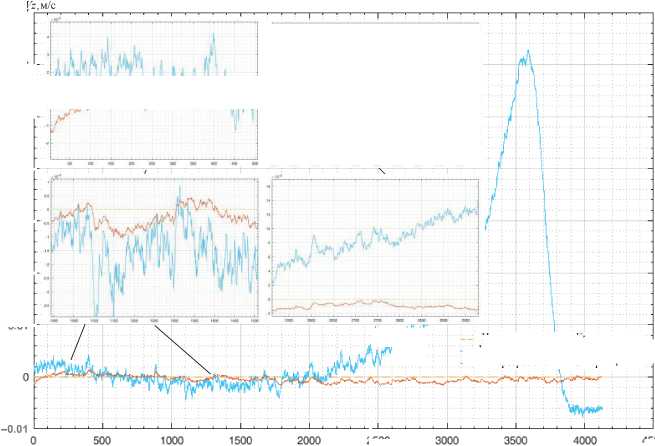
Рис. 3. Функциональные зависимости оценок Vz КО от метода формирования матрицы Q

Истинное значение Vz

— Vz - метод уточнения ковариации

— Vz - разработанный алгоритм

Результаты анализа функциональных зависимостей оценок составляющих вектора скорости КО от метода формирования матрицы Q позволяют сделать вывод, что при использовании метода ковариации в адаптивном алгоритме фильтрации параметров движения КО на ГСО к недостоверному определению ТПКО в части ложного обнаружения маневра.

48 выпуск 2/2020

отклонений (СКО) оценок модуля вектора скорости КО

На рисунке 4 представлены функциональные зависимости средних квадратических (о|VКО I) от метода форми-

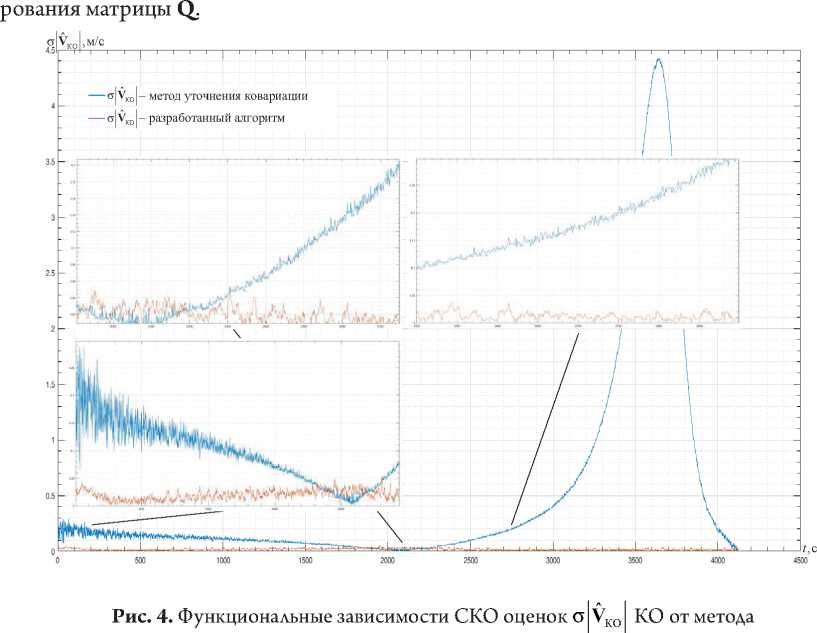
формирования матрицы Q

Результаты анализа функциональных зависимостей оценок составляющих вектора скорости КО и СКО оценок модуля вектора его скорости от метода формирования матрицы Q позволяют сделать вывод, что решение задачи обнаружения маневра КО при маневрировании с малой тягой двигательной установки возможно с использованием разработанного адаптивного алгоритма фильтрации параметров движения КО на основе модифицированного метода уточнения ковариации.

Заключение

Таким образом, разработанный алгоритм сочетает в себе простоту реализации и высокую точность оценок параметров движения КО на ГСО при обеспечении сходимости процесса фильтрации.

Реализация разработанного адаптивного алгоритма фильтрации параметров движения КО на основе модифицированного метода уточнения ковариации позволит за счет снижения погрешностей оценок параметров движения КО повысить достоверность ТПКО на ГСО.