Адаптивный алгоритм интерполяции для иерархической компрессии изображений

Иерархическая компрессия изображений [1-3] основана на многократном прореживании исходного изображения, использовании прореженного изображения для интерполяции пропущенных отсчетов и последующем кодировании интерполяционных ошибок. Поэтому эффективность иерархической компрессии во многом определяется эффективностью используемого алгоритма интерполяции. Применяемые в настоящее время алгоритмы интерполяции [4, 6], как правило, заключаются в простом усреднении по ближайшим отсчетам и никак не учитывают особенности обрабатываемого изображения. Поэтому актуальной является задача разработки нового адаптивного алгоритма интерполяции, который был бы более эффективен за счет настройки на каждое конкретное изображение.

В данной работе предлагается новый адаптивный алгоритм интерполяции, который настраивается на изображение за счет использования нескольких интерполирующих функций и параметризованного решающего правила. Рассматривается использование этого алгоритма для конкретного метода компрессии, реализующего иерархический подход.

Метод компрессии на основе ИСИ

Будем рассматривать метод компрессии на основе иерархической сеточной интерполяции (ИСИ) [5,6]. Пусть X = { x ( m , n )} - исходное изображение. Рассмотрим представление изображения X в виде объединения иерархических уровней X _l :

L - 1

X = и XI ’ l=0

X L-1 = { xL-1 (m, n )},

X i ={ xl (m, n)}/{xi+1 (m, n)}, l < L - 1,(3)

где L      – количество уровней, а {xl (m, n)}      - массив отсчетов изображения, взятых с шагом 2l по каждой координате.

Представление (1)-(3) дает возможность при компрессии и декомпрессии обрабатывать уровни последовательно, начиная со старшего уровня X _{L -} 1 , причем отсчеты каждого более старшего (менее детального) уровня будут использоваться для интерполяции отсчетов младшего (более детального) уровня.

Количество уровней выбирается таким образом, чтобы объем старшего (наиболее прореженного) уровня был пренебрежимо мал по сравнению с объемом данных всего изображения, поэтому старший уровень может быть записан в сжатое изображение и без компрессии. Процедура компрессии любого из следующих младших уровней X l, l < L -1 включает сле- дующие этапы (см. также рис. 1):

• 1)    Интерполяция .

Производится интерполяция отсчетов {xl (m, n)} уровня X l на основе отсчетов {xk (m, n), k > l} уровней {Xk, k > l}, уже прошед- ших компрессию и восстановление:

I l-1                     | xl( m,n ) = P I U{xk(m,n) }| ,

V k = l + 1              J

где x l ( m , n ) - интерполирующие значения отсчетов, а P ( .. ) - функция, задающая в общем виде некоторый интерполятор. Конкретные примеры интерполяторов приведены в следующем разделе.

• 2)    Вычисление постинтерполяционных остатков

Вычисляется массив разностей истинных и интерполирующих значений отсчетов («постинтерполяционных остатков»):

f l ( m , n ) = x i ( m , n ) - x l ( m , n ) . (5)

• 3)    Квантование постинтерполяционных остатков

Выполняется квантование постинтерполяционных остатков (5). В данной работе используется квантователь, гарантирующий, что декомпрессированное изображение будет отличаться от исходного не более, чем на величину заданной максимальной ошибки £ max :

q l ( m , n ) = sign ⁽ f ( m , n ) )

| ^fl ^{( m} , ⁿ )| + ^£ max

£ max

+ 1

, (6)

где [.. ] обозначает выделение целой части.

• 4)    Вычисление восстановленных значений отсчетов

По квантованным значениям постинтерполяционных остатков вычисляются восстановленные значения x i ( m , n ) отсчетов уровня. Очевидно, что для этого необходимо сначала вычислить восстановленные значения постинтерполяционных остатков:

f l ⁽ m , n ) = q l ⁽ m , n ^{) ( 2 £} ma_x + 1 ) ,                  (7)

а затем осуществить собственно восстановление:

x i ( m , n ) = f l ( m , n ) + x l ( m , n ) .                  (8)

Эти восстановленные отсчеты будут нужны для интерполяции более младших иерархических уровней { X k , k <  I } .

• 5)    Статистическое кодирование

Осуществляется статистическое кодирование квантованных постинтерполяционных остатков. Поскольку распределение их вероятностей, как правило, является существенно неравномерным, в результате кодирования можно достичь значительного сокращения объема данных, которое и является целью выполняемой обработки изображения. На этом описание процедуры компрессии закончено.

Процедура декомпрессии уровня X l , I <  L - 1

включает следующие этапы:

• 1)    Декодирование

Производится декодирование квантованных значений постинтерполяционных остатков (6).

• 2)    Интерполяция

Производится интерполяция вида (4) по восстановленным отсчетам.

• 3)    Восстановление

Как и при компрессии, производится деквантование (7) и вычисление восстановленных значений отсчетов (8). На этом описание процедуры декомпрессии закончено.

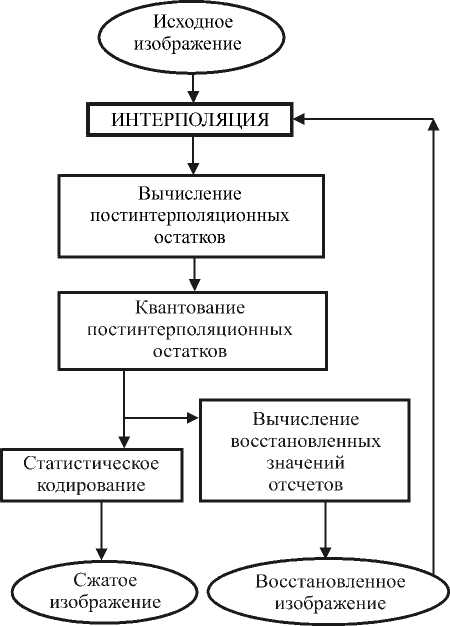
Рис. 1. Схема процедуры компрессии

Известные схемы интерполяции

Основными требованиями к интерполятору являются как можно более высокая точность при ма- лой вычислительной сложности. Поэтому обычно для интерполяции используют алгоритмы (схемы), которые заключаются в простом усреднении по ближайшим восстановленным отсчетам (см. рис 2). Эти схемы работают одинаково и при компрессии и при декомпрессии.

Будем отдельно рассматривать два типа интерполируемых отсчетов. Отсчеты вида xt (2m +1,2n +1) будем называть «центральными» (см. рис. 3). Нетрудно видеть, что четыре ближайших восстановленных отсчета более старшего уровня находятся по диагонали от центрального. Отсчеты вида   xl (2 m +1,2 n)   и xl (2m,2n +1) будем называть "крайними" (см. рис. 4). Два ближайших восстановленных отсчета более старшего уровня находятся по вертикали или по горизонтали от крайнего. Укажем способы интерполяции одного крайнего и центрального отсчетов для каждой схемы. Схема (I):

x l ( 2 m + 1,2 n ) = { x i ( 2 m ,2 n ) , x i ( 2 m + 2,2 n ) ) , (9)

x l ( 2 m + 1,2 n + 1 ) = { x i ( 2 m ,2 n ) , x i ( 2 m + 2,2 n ) x i ( 2 m ,2 n + 2 ) , x i ( 2 m + 2,2 n + 2 ) )

где { .. ) обозначает усреднение с последующим округлением до ближайшего целого.

Схема (II):

Сначала с помощью выражения вида (9) интерполируются все крайние отсчеты. Затем для них вычисляются восстановленные значения, которые используются для интерполяции центральных отсчетов xi (2 m +1,2 n +1) = { xi (2 m +1,2 n), xi (2 m ,2 n +1), xi (2 m +1,2 n + 2), xi (2 m + 2,2 n +1))

Схема (III):

Сначала с помощью выражения вида (10) интерполируются все центральные отсчеты. Затем для них вычисляются восстановленные значения, которые используются для интерполяции крайних отсчетов xi (2m +1,2n) = ( xi (2m, 2n) , xi (2m + 2,2n) , (12) xi (2m +1,2n-1) , xi (2m +1,2n +1) )

Достоинством рассмотренных известных схем является низкая вычислительная сложность. Общим недостатком этих схем является то, что они всегда работают одинаково, т.е. никак не учитывают ни особенностей обрабатываемого изображения, ни локальных особенностей обрабатываемого участка.

Адаптивная схема интерполяции

Основной идеей адаптивного интерполятора является использование не одной, а нескольких интерполирующих функций. Решение о том, какая именно из этих функций будет использована в каждой конкретной точке изображения, принимается на основе решающего правила, зависящего от парамет- ров. При этом собственно обработке данных предшествует процесс обучения (настройки решающего правила), который заключается в отыскании оптимальных значений этих параметров.

При работе этого алгоритма, также как и для схемы (III), сначала производится интерполяция всех центральных отсчетов, а затем, на основе восстановленных значений центральных отсчетов, осуществляется интерполяция крайних отсчетов. Рассмотрим три интерполирующие функции центрального отсчета (см. рис. 3).

x ⁽⁰⁾ ( 2 m + 1,2 n + 1 ) = { x i ( 2 m ,2 n ) , x i ( 2 m + 2,2 n + 2 ) ) (13)

x ⁽¹⁾ ( 2 m + 1,2 n + 1 ) = { x i ( 2 m ,2 n ) , x i ( 2 m + 2,2 n ) , x i ( 2 m ,2 n + 2 ) , x i ( 2 m + 2,2 n + 2 ) )

x }²⁾ ( 2 m + 1,2 n + 1 ) = { x i ( 2 m + 2,2 n ) , x i ( 2 m ,2 n + 2 ) ) (15)

Выбор функции, которая будет использована для интерполяции в каждой точке, осуществляется на основе признака ц (2 m +1,2 n +1) = |xi (2 m ,2 n) - xi (2 m + 2,2 n + 2) | - |x; (2 m ,2 n + 2)-x (2 m + 2,2 n )|

с помощью зависящего от параметров а и в решающего правила

[0, ц < а;

Fr(ц,а,в)=к а< ц < в; (17) [2, ц > в;

которое в каждой точке по значению признака определяет номер используемой интерполирующей функции. Предполагается, что оба параметра целочисленные, причем а < 0, а в - 0 . Собственно адаптивный интерполятор задается выражением xi(m,n)= xij) (m,n), j = Fr(ц (m,n),а,в)- (18)

Поясним такое построение интерполятора. Нетрудно видеть, что большие значения признака (18) соответствуют, например, ситуации, когда через интерполируемый центральный отсчет проходит диагональный контур, имеющий направление «слева снизу вправо вверх». Причем чем лучше выражен контур, том больше значение признака. Если признак больше порогового значения в , то будет выбрана интерполирующая функция (15), реализующая интерполяцию «вдоль контура» (см. рис. 3-(3)). В контурных точках такая интерполяция является более точной, за счет чего и достигается выигрыш.

Аналогичным образом рассматривается ситуация с диагональным контуром направления «слева сверху вправо вниз» (см. рис. 2-(1)), которая «регулируется» параметром а . В случае, если выраженного диагонального контура не присутствует, то используется «обычное» усреднение вида (14).

Параметры а ив играют роль пороговых величин, на которых происходит переключение на интерполяцию «вдоль контура». Чем меньше на изо- бражении контуров, тем больше по модулю значения этих параметров.

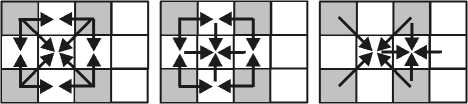
(I)                   (II)                     (III)

Рис. 2. Известные схемы интерполяции

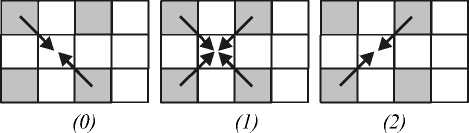
Рис. 3. Адаптивная интерполяция центрально отсчета

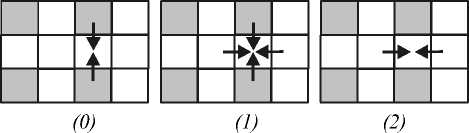
Рис. 4. Адаптивная интерполяция крайнего отсчета

Перед собственно применением интерполятора (18) производится его обучение (настройка на конкретное изображение), которое заключается в отыскании оптимальных значений параметров а и в • Для этого в данной работе используется критерий минимизации суммарной ошибки интерполяции

E X) ( а , в ) = 21 x i ( m , n ) - x i ( m , n )| ^ min, (19) а , в

( m , n ) e Ii                                         '

где I_l – множество индексов центральных отсчетов уровня X _l .

Рассмотрим алгоритм поиска параметров. Двухпараметрическая задача оптимизации (19) допускает декомпозицию на две однопараметрические задачи. Для этого рассматриваются множества индексов I , ’, I ⁽⁰ и I^ , для которых значение признака ц ( m , n ) соответственно отрицательно, равно нулю и положительно. Тогда суммарная ошибка интерполяции (19) может быть записана в виде

E i^ ( а , в ) = Е ^) ( а ) + E (⁰⁾ + E i ⁺ ( в ) , (20) где E_i ^⁺^ ( в ) — суммарная ошибка интерполяции по точкам с положительным значением признака

Ei(+) (в )= 21 xi(m,n)-xi(m,n )l, (21) ( m, n )e I+ которая зависит только от одного параметра в. Величины E^ (а) и E(0) вводятся аналогичным образом через множества li ^ и I(0).

Теперь оптимальное значение параметра в можно определить как минимум одномерной функ- ции (21) на интервале [0, M) , где M = max{x(m,n)}+1. Для этого в процессе обучения заполняется матрица E(+) = {Ei к): i = 1,2; k е [1, M)}:

E S^; =    E x li) ^{( m} , n ^)- x i ^{( m} , n )| ,           ⁽²²⁾

( m , n ) e I ^{( k} )

где I_l ^{( k )} – множество индексов, для которых значение признака ц ₁ ( m , n ) равно k . После того, как эта матрица заполнена, значение минимизируемой функции (21) вычисляется для всех значений аргумента с помощью следующих выражений:

M - 1

Е^ (0)=E E 2+E и=1

p(+)(— F(+Чй И F(+) -i- F(+)

El (e) = El (e -1)-E2,в + E1,в ,

Следует отметить, что при проведении расчета (23)-(24) и при собственно поиске минимума функции (21) производится работа не с изображением, а со вспомогательной матрицей E , благодаря чему вычислительная сложность этого этапа пренебрежимо мала и не зависит от размера изображения.

Определение оптимального значения параметра а осуществляется аналогичным образом, исходя из минимизации функции Е ^ - ) ( а ) , с использованием матрицы E ^{( - )}, которая строится аналогично матрице E ^{( + )}. Заполнение обоих матриц осуществляется за один проход по изображению и добавляет к вычислительной сложности 4 операции на отсчет. После того, как оптимальные значения параметров определены, они сохраняются в сжатом изображении и используются для обработки интерполятором (18).

Таким образом, алгоритм интерполяции центрального отсчета на этапе компрессии включает следующие шаги:

• 1)    Обучение: вычисление оптимальных значений параметров (первый проход по изображению):

• a)    вычисление интерполирующих значений (13)-(15) и признака (16) для всех центральных отсчетов;

• b)    заполнение матриц E ^{( - )} и E ^{( + )};

• c)    отыскание оптимальных значений параметров а и в как минимумов функций E l ~) ( а ) и E_l⁽⁺⁾ ( в ) с использованием выражений вида (23)-(24);

• 2)    Сохранение оптимальных значений параметров а и в в сжатом изображении.

• 3)    Собственно интерполяция (второй проход по изображению), которая заключается в применении функции (18) ко всем центральным отсчетам при оптимальных значениях параметров а и в .

В отличие от известных интерполяционных схем, разработанный алгоритм на этапе декомпрессии работает не так, как на этапе компрессии. А именно, при декомпрессии интерполяция не требует обучения и включает следующие шаги:

• 1)    Чтение из сжатого изображения оптимальных значений параметров а и в .

• 2)    Собственно интерполяция (единственный проход по изображению), которая заключается в применении функции (18) ко всем центральным отсчетам при оптимальных значениях параметров а и в .

Как при компрессии, так и при декомпрессии, после интерполяции центральных отсчетов для них вычисляются восстановленные значения, которые используются для интерполяции крайних отсчетов. Интерполятор крайних отсчетов работает в целом аналогично интерполятору центрального отсчета. Интерполяция по-прежнему производится по четырем ближайшим отсчетам, но теперь они расположены не по диагонали, а по вертикали и по горизонтали от интерполируемого (см. рис. 4). Другими словами, вся ситуация «поворачивается» на 45 градусов. Соответственно, при интерполяции будут отслеживаться не диагональные, а вертикальные и горизонтальные контура.

Важно подчеркнуть также тот факт, что из построения адаптивного интерполятора видно, что в вырожденном случае (при а = - M + 1, в = M — 1) он сводится к схеме (III). Другими словами, по точности построенный интерполятор гарантированно будет работать не хуже, чем интерполятор (III).

Таким образом, можно сформулировать следующие преимущества разработанного адаптивного интерполятора:

• 1.    Учет локальных особенностей изображения за счет использования нескольких интерполирующих функций;

• 2.    Настройка на каждое конкретное изображение за счет использования параметризованного решающего правила;

• 3.    Гарантия точности не хуже, чем у схемы (III);

• 4.    Структурно простая схема обработки.

Сравнение интерполяционных схем

Для определения эффективности разработанного адаптивного интерполятора, который далее будем называть схемой (IV), было проведено его сравнение с известными схемами (I), (II), (III), которые описываются выражениями (9)-(12). В задаче компрессии эффективность любой интерполяционной схемы определяется ее вычислительной сложностью и степенью сжатия, которая может быть достигнута с применением этой схемы.

Если считать, что деление на степени двойки не требует арифметических операций, то все четыре описанные схемы реализуются исключительно аддитивными операциями. Вычислительные сложности для всех схем в аддитивных операциях на отсчет приведены в таб. 1.

Из таблицы видно, что вычислительная сложность разработанной схемы (IV) больше, чем сложность из- вестных схем интерполяции, однако для большинства приложений является вполне допустимой.

Таблица 1. Вычислительная сложность интерполяционных схем

Схема интерполяции	(I)	(II)	(III)	(IV)
Вычислительная сложность при компрессии	5 3	5 3	3	11
Вычислительная сложность при декомпрессии	5 3	5 3	3	6

Для сравнения схем интерполяции по степени компрессии изображений в рамках метода ИСИ был проведен вычислительный эксперимент. Для эксперимента использовались изображения типа «космический снимок», одно из которых показано на рис. 5.

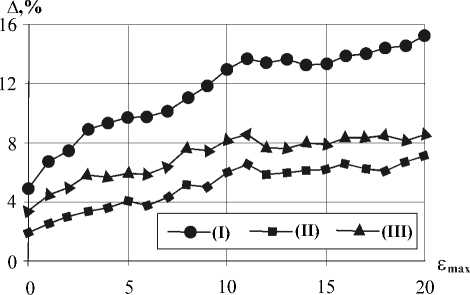
Рис. 6. Оценка выигрыша в размере сжатого изображения разработанной схемы интерполяции над известными схемами

Рис. 5. Изображение вида «космический снимок»

Для всех изображений схема (IV) обеспечила меньший объем сжатого изображения, чем схемы (I), (II), (III). Для количественного описания этого выигрыша использовались величины вида

• ( I )    ( IV )

^S _{S ( I} ^S ₎ 100% , (25) где S ^{( I )} , S ^{( IV )} - размеры сжатых изображений для схем (I) и (IV) соответственно. Аналогичным образом вычислялись величины ∆ ^{( II )} и ∆ ^{( III )} . Типичные результаты, полученные при различных максимальных ошибках для изображения на рис. 5, показаны на рис. 6.

Как видно из рис. 6, величины вида (25) для всех трех известных схем всегда положительны. Следовательно, на всем рассматриваемом диапазоне максимальных ошибок разработанная схема (IV) имеет устойчивое преимущество, которое, вообще говоря, увеличивается с ростом ошибки. При этом преимущество над самой лучшей из известных схем достигает 6-7% на половине рассматриваемого диапазона, что на практике позволяет обеспечить значительную экономию емкости запоминающих устройств.

Заключение

В работе предложен новый адаптивный алгоритм интерполяции для иерархической компрессии изображений. Данный алгоритм обеспечивает выигрыш по степени сжатия по сравнению с известными алгоритмами интерполяции. Разработанный алгоритм может быть эффективно использован в прикладных задачах, связанных с обработкой, хранением и передачей сжатых цифровых изображений.