Адаптивный алгоритм сегментации изображений

Задача сегментации изображений является актуальной в настоящее время. Она может решаться различными способами, например методом наращивания областей, сегментацией по порогу (в простейших случаях), методом расщепления-слияния областей. Также одним из широко известных способов является сегментация на основе марковских случайных полей. При использовании этого метода эффективность работы алгоритма сегментации зависит от параметров локальной области, используемой для сегментации каждой точки изображения X. Под локальной областью n

L={( i,j ): 1 <  i <  h, 1 <  j < w} ) изображения X понимается множество соседних точек { ni, j } прямоугольной сетки L , то есть n = {и^ с Цу )е L^}, причем (i, j ) e n i , j и (k, l )e ni, j , откуда следует, что ( i , j ) g nk i . Обычно при выполнении сегментации используется локальная область размером элемента. Для повышения эффективности работы алгоритма сегментации увеличивают размер локальной области. Размер локальной области в таком случае подбирается на основе эксперимента. С увеличением размера локальной области увеличивается временная сложность алгоритма. Поэтому, предлагается использовать марковские случайные поля с локальной областью, рассчитываемой на основе статистических свойств изображения. Это позволит в полной мере использовать характерные особенности изображения для повышения качества решения задачи сегментации и снижения временной сложности работы алгоритма сегментации.

Постановка задачи исследования

Целями исследования являются:

• 1)    изучение возможности применения адаптивной локальной области к существующим алгоритмам сегментации на базе марковских случайных полей;

• 2)    оценка эффективности работы предложенного подхода;

• 3)    рассмотрение особенностей, возникающих вследствие применения адаптивной локальной области.

Сегментация изображений на базе марковских случайных полей

Множество точек изображения { x i j } называется марковским случайным полем относительно ( L,n\ если [1-2]:

p ( x i , j | X k ,l, (k, l ) еЛ ) = P⁽X i , j | X k ,i, ⁽k, l )

^е ni, j ) ,

где Λ – любое конечное множество подмножеств точек сетки L, которое содержит {ni, j}, но не (i, j). С каждой точкой изображения X связывается метка ®i, j , принадлежащая множеству меток toi, j е Q, которая при выполнении сегментации определяет к какому классу объектов изображения X относится рассматриваемая точка. Задача сегментации изображения X на основе случайного поля Гиббса, которое используется для упрощения расчетов [3, 4] состоит в поиске оптимальной разметки ω, которая минимизирует функцию энергии U(ю). Допустим, что каждый класс объектов λ ∈ Λ изображения X будет описываться средним μλ и дисперсией σλ. В таком случае функция энергии записывается следующим образом [1; 5]:

( X i, j

+

и w = 2 2 iog(-& „, _v.)

i = 1 j =1

-

⎞

^ ® i , j /

2 σ ²

®i, j

■ +

⎠

⎝

+ii 22 2 Vk (^i.j), i=1 j=1ck gC где C – множество клик для рассматриваемой локальной области n [4],

C = {ck },

Vk к®.,] ) = *

+ в _k , если все m i , j в клике равны, _<- в _k , иначе в k ^ 0-

Для выполнения сегментации (т.е. для минимизации функции энергии) могут быть использованы различные алгоритмы: Iterated c onditional Mode [6], Metropolis Dynamics [7], Modified Metropolis Dynamics [7], Simulated Annealing [1], Mean Field Annealing [8], Graduated Non Convexity [9]. В [5, 10] показано, что наибольшую эффективность, с точки зрения качества сегментации, имеет алгоритм Modified Metropolis Dynamics.

Рассмотрим подход для вычисления адаптивной локальной области n .При поиске структуры локальной области n в качестве критерия оптимальности можно воспользоваться величиной взаимной информации I ( X,Y ). Величина взаимной информации I ( X,Y )показывает сколько информации о изображении X содержится в изображении Y [11-12]:

I (X,Y)= 22 ^p X ,Y )ю_в -*X^ , где X,Y – изображения; p ( X ), p ( Y ) – плотности распределения вероятностей изображений X и Y , p ( X , Y ) – совместная плотность распределения изображений X и Y . Предлагаемый метод основан на вычислении величины взаимной информации для каждого элемента локальной области n размером PxP с центром в точке (xo, уо) , где P - нечетное число.

Предположим, необходимо вычислить величину взаимной информации между центральным элементом локальной области n и элементом с координатами (k, l ) , который принадлежит локальной области. Для этого выполним сдвиг исходного изображения X таким образом, чтобы элемент с координатами ( k , l ) переместился в центр локальной области. Для выполнения этой операции надо выполнить сдвиг изображения на k элементов по оси OX и на I элементов по оси OY : X((xo - к ),( y o - 1 )) .

Выполнив эту операцию для исходного изображения и получив, таким образом, изображение Y, вычислим величину взаимной информации между исходным X и смещенным Y изображениями. Полученная величина и будет являться взаимной информацией между элементом локальной области с координатами ( k , l ) и центральным элементом локальной области (xo, .yo) .

Рассмотрев все возможные перемещения из некоторого элемента в центр локальной области, т.е. рассмотрев все возможные (в рамках локальной области) сдвиги исходного изображения получим матрицу величин M i (х , y ) взаимной информации между центральным элементом локальной области и всеми остальными элементами локальной области.

Результирующая матрица величин взаимной информации M i (х y ) может быть использована для определения структуры локальной области. Для этого можно применить процедуру отсечения по порогу:

_ f1, MI(X,Y)(k, l ) ^ Thr, nk,l [0, Mi(x,y)(k, l) < Thr ’ где Thr & [0; 1] - порог, определяемый экспериментальным путем.

Тестовые изображения

Естественные (или реальные) изображения часто имеют различные свойства в различных направлениях (вертикальном, горизонтальном, диагональном, а также в других), что выражается в том, что вычисленная локальная область каждого элемента изображения также будет иметь направленный характер. Поэтому, стоит задача разработки тестовых изображений, которые имеют такие же свойства (или часть свойств) естественных изображений, для оценки качества работы алгоритмов сегментации.

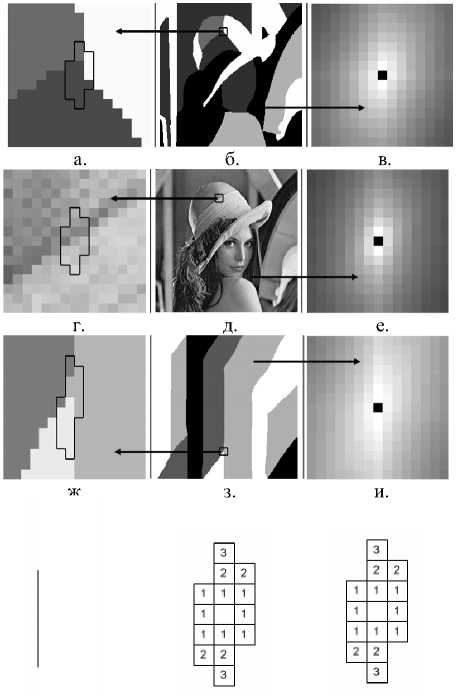
Как было выяснено в ходе проведения экспериментов, именно ориентация значи- тельных по размерам областей изображений относительно друг друга определяет форму локальной области. Если изображение содержит вытянутые по вертикали и ориентированные под некоторым углом многоугольники, то и вычисленная, на основе предложенного выше подхода, локальная область такого изображения будет вытянута по вертикали и ориентирована под некоторым углом. Также, если рассматривать вычисленные локальные области естественного изображения и его сегментированной ручным образом версии,то их локальные области будут мало отличаться (см. рис. 1 ). Таким образом, в качестве тестовых изображений можно рассматривать как искусственно созданные изображения, так и вручную сегментированные естественные.На рис. 1 показаны два типа тестовых изображений, естественное изображение, а также локальные области этих изображений. Для оценки эффективности работы алгоритма можно рассмотреть влияние шума на результат сегментации. Как показывают эксперименты, искажение изображения действует на размер и форму локальной области (см. рис. 2).

Оценка качества сегментации

В [1 3] рассматривается подход к оценке качества выполнения сегментации, который заключается в следующем. Допустим, что имеется исходная карта расположения n -го класса объекта на изображении C r (n) ( 1 < n <  N , N - число классов объектов) и карта, полученная в результате выполнения сегментации C (n) , тогда можно выделить два типа ошибок:

• 1)    ошибка первого типа ei (n) возникает, когда точка присутствует в C r ( n ) и не присутствует в C (n) ;

• 2)    ошибка второго типа e2 (n) возникает, когда точка не присутствует в C r (n) и присутствует в C ( n ) .

Ошибка первого типа вычисляе т ся следующим образом: ei (n) = card (с (n) П C r ⁽ n )) , где card (X) – мощность множества X .

Ошибка второго типа в ычисляется следующим образом: e2 (n) = card ( c (n) n C r ⁽ n )) .

Если рассматривать изображение в целом, то изменение в одном классе приводит к изменениям в другом (расположенным рядом). Поэтому, для оценки качества сегментации можно использовать ошибку только первого или только второго типа.

л.

м.

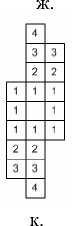
Рис. 1. Оценка структуры локальной области: а, г, ж – вычисленные локальные области тестовых изображений; б, д, з – тестовые изображения; в, е, и – матрицы взаимной информации тестовых изображений (для изображения в. Thr = 0,85 , для е. Thr = 0,85 , для и. Thr = 0,72 ); к, л, м – локальные области для изображений б, д, з

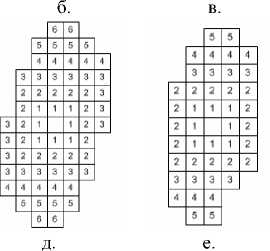
Рис. 2. Влияние шума на локальную область; а-в: зашумленные тестовые изображения, показанные на рис. 1 (а: ПОСШ = 20,4633, б: ПОСШ = 20,2168, в: ПОСШ = 20,2510), г-е: структуры локальных областей зашумленных тестовых изображений

Эксперимент

Для проведения эксперимента использовалось тестовое изображение, приведенное на рис. 1з. Для внесения искажений использовался гауссов шум с дисперсией о n . Эксперименты проводились для двух видов локальных областей:

• -    адаптивной локальной области;

• -    фиксированной локальной области.

При оценке влияния типа локальной области на работу алгоритма рассматривались следующие параметры.

• 1)    TI – время одной итерации алгоритма сегментации (в секундах);

• 2)    I – число итераций алгоритма сегментации;

• 3)    C – число клик в локальной области;

• 4)    E – ошибка сегментации.

На рис. 3 приведены результаты сегментации изображения, показанного на рис. 1з. В таблице 1 приведены результаты экспериментов. В первом эксперименте о n = 0,01 (вычисленный Thr = 0,92 ), во втором оn = 0,04 ( Thr = 0,941 ), в третьем оn = 0,06 ( Thr = 0,941 ).

В таблице 1 поле «Локальная область» означает используемую локальную область: адаптивную «A» или фиксированную «F».

Illflfli а.                б.                 в.                 г.

Рис. 3. Результаты сегментации тестового изображения: а, в) с использованием адаптивной локальной области (а: о_и = 0,06; в: а_п = 0,04); б, г) с использованием фиксированной локальной области (б: с_п = 0,06 ; г: а_п = 0,04)

Таблица 1. Результаты экспериментов

№ эксперимента	Локальная область	TI	I	C	E
1	A	0,32	35	14	102
	F	0,46	51	24	175
2	A	0,53	152	27	1087
	F	0,62	160	37	1693
3	A	0,62	197	29	4020
	F	0,91	259	39	6121

Видно, что по сравнению с фиксированной локальной областью, использование адаптивной локальной области позволяет улучшить результат сегментации.

По результатам выполнения экспериментов можно сформировать следующие рекомендации по настройке параметров алгоритма:

• 1)    При выборе каждой новой клики необходимо рассматривать только те клики, которые включают еще не использованные точки локальной области (т.е. основной принцип – не многократное использование одного и того же набора точек локальной области, а использование новых точек). Некоторые точки локальной области нельзя включить в клику, вследствие геометрии локальной области и правила, по которому точки включаются в локальную область: допустим, существуют две точки локальной области L : a и b , локальные области которых обозначаются, как L _a и L _b , причем относительно точки a происходит отсчет клик (т.е. она всегда включена в клику, в рассматриваемом случае точка a является точкой, для которой вычисляется метка) тогда точка b включается в клику C , если b ∈ L _a и a ∈ L _b ; например, для точки l (см. рис. 4) точка 2 входит в локальную область точки 1, при этом точка 3 не входит в локальную область точки 2, это приводит к выбору клики для этих точек, показанной на рис. 4.

• 2)    Если результаты сегментации не являются удовлетворительными, то можно уменьшить порог Thr , который отвечает за выбор локальной области. Такой выбор локальной области будет более обоснован, чем выбор локальной области простым увеличением порядка рассматриваемой области на единицу.

• 3)    При выборе клик необходимо, чтобы соблюдалось равновесие между числом клик разной ориентации (имеющими вертикальную, горизонтальную или другую направленность). Такая проблема не возникает при использовании локальной области с одинаковыми размерами по горизонтали и вертикали и является актуальной для локальных областей с различными размерами по горизонтали и вертикали (см. рис. 2д). При отсутствии равновесия результат сегментации может иметь искажения, которые будут вызваны преобладанием клик определенного типа (например, в случае преобладания вертикальных клик это может привести к удалению некоторых горизонтально ориентированных объектов с сегментированного изображения). Также к искажению изображения могут привести слишком большие клики (см. рис. 3б).

• 4)    При выборе клик наибольшее влияние на результат сегментации будут оказывать те клики, которые наиболее близко расположены к центру локальной области, при этом, отдаленные клики

могут незначительно улучшать качество сегментации (убирать шум, это также говорит о преимуществе использования адаптивной локальной области перед фиксированной).

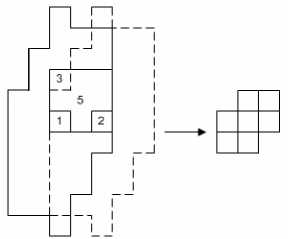
Рис. 4. Формирование клики

По результатам экспериментов можно сделать следующие выводы.

• 1.    Использование адаптивной локальной области позволяет улучшить эффективность работы алгоритма сегментации по ряду параметров (число итераций алгоритма, время одной итерации, ошибка сегментации).

• 2.    Использование априорных данных позволяет обоснованнее подходить к выбору локальной области.

• 3.    Увеличение числа рассматриваемых клик не всегда позволяет повысить качество сегментации.

• 4.    Добавление клик не соответствующих статистическим свойствам изображения (по направленности) не приводит к улучшению результата сегментации.

Заключение

В настоящее время многие работы в области цифровой обработки изображений ориентированы на повышение эффективности работы существующих алгоритмов, на создание адаптивных методов обработки изображений. В работе предлагается подход к сегментации изображений на базе марковских случайных полей с использованием адаптивной локальной области. Расчет локальной области производится на базе критерия взаимной информации. В работе рассмотрен ряд вопросов, связанных с практической реализацией и некоторые особенности, возникающие вследствие использования адаптивной локальной области. Эффективность работы алгоритма подтверждается экспериментальными данными. Разработанный подход, заключающийся в использовании адаптивной локальной области является достаточно общим и может быть применен для любых алгоритмов сегментации, перечисленных выше.