Адаптивный алгоритм стеганографического встраивания данных в цифровые изображения, использующий некриптографические хеш-функции для их извлечения

Современные технологии компьютерной и цифровой стеганографии позволяют решать целый ряд задач, связанных с защитой конфиденциальной информации, находящейся в публичном доступе, а также задач, связанных с контролем распространения и использования различных объектов цифрового контента. Методы стеганографии реализуют скрытное внедрение пользовательских, аутентификационных или идентификационных данных (сообщений) в произвольные цифровые объекты (контейнеры), которые могут храниться в открытом виде или передаваться по незащищённым каналам коммуникации.

Одной из основных задач, которую приходится решать при разработке стегоалгоритмов, является минимизация неизбежных искажающих изменений в контейнерах, возникающих при встраивании в них сообщений. Вносимые искажения должны быть визуально и статистически незаметны и не должны нарушать функциональности контейнеров. Вторая задача, которая может ставиться при разработке стегоалго-ритмов, связана с повышением их пропускной способности (ПС) U =|M |/| I |, оцениваемой как отношение размера скрываемого сообщения M к размеру контейнера I. В классических стегосистемах, предполагаю- щих наличие контейнера и операций по его модификации, увеличение ПС почти неизбежно сопровождается увеличением искажающих изменений носителя.

Современные алгоритмы пространственной стеганографии, такие как WOW [1], S-UNIWARD [2], HUGO [3], реализуют идею адаптивного внедрения сообщений, решая задачу минимизации искажений путём целенаправленного выбора для внедрения данных лишь наиболее стохастичных областей контейнера, искажения в которых невозможно или достаточно сложно обнаружить даже с привлечением современных методов стегоанализа. К ограничениям данных и подобных им алгоритмов можно отнести сравнительно невысокую ПС, а также (зачастую) необходимость наличия исходных незаполненных контейнеров для извлечения данных. Среди алгоритмов адаптивной пространственной стеганографии, отличающихся повышенной ПС, можно отметить алгоритм MPBDH [4], реализующий блочное скрытие и модифицирующий до нескольких младших битовых плоскостей блоков изображения-контейнера в зависимости от их «сложности», а также алгоритм [5], реализующий встраивание информации лишь в наиболее шумные участки пространственного представления носителя путём перезаписи их младших разрядов (не более 4) битами сообщения. К объективным недостаткам ал- горитмов с высокой ПС можно отнести их меньшую устойчивость по отношению к современным методам стегоанализа.

Алгоритмы стохастической модуляции [6, 7] минимизируют не абсолютные искажения контейнеров, а их статистические отличия от естественных незаполненных контейнеров путём внесения в них дополнительных шумов с заданными вероятностными распределениями, имитирующих естественные шумы контейнеров соответствующих форматов. В работе [8] минимизация статистических искажений графических контейнеров реализуется путём выделения высокочастотных стохастических составляющих самих контейнеров с последующим маскированием встроенных сообщений данными составляющими. Общий уровень искажений контейнеров, вносимых алгоритмами стохастической модуляции, может быть существенно выше, чем для алгоритмов адаптивного пространственного скрытия.

PVD-алгоритмы (Pixel Value Difference) пространственной стеганографии кодируют биты скрываемых сообщений как разность модифицированных значений пикселей блоков заданной конфигурации. В работах [9, 10] предложены адаптивные схемы скрытия на основе PVD, учитывающие информацию о вертикальных, горизонтальных и диагональных краях объектов на изображении, что позволяет минимизировать искажающие изменения маркированных контейнеров и обеспечить высокую устойчивость к PDH и RS-стегоанализу.

Особняком стоят появившиеся в последние годы алгоритмы [11 – 14], реализующие принципы «стеганография без контейнеров» (Coverless Steganography). Как следует из названия, они не используют традиционные контейнеры и не решают задачу минимизации их искажений. Скрываемая информация «кодируется» с использованием выборки объектов из предварительно сформированной большой коллекции объектов, например, набора изображений, каждый из которых может быть преобразован в короткую бинарную строку, соответствующую определённой части сообщения. На практике для преобразования объектов из выборки во фрагменты сообщения могут применяться различные алгоритмы классического и робастного хеширования [15]. В случае использования робастного хеширования передаваемые по открытым каналам объекты, кодирующие сообщение, могут быть дополнительно искажены, но это не должно существенным образом отразиться на возможности восстановления сообщения. Основным достоинством подобной схемы скрытной коммуникации является отсутствие любых стеганографических модификаций передаваемых объектов, т.е. абсолютная стеганографическая стойкость. К числу недостатков coverless-алгоритмов можно отнести невысокую ПС.

Также стоит отметить набирающие популярность стегоалгоритмы, реализующие принцип «стеганогра- фия без встраивания» (Steganography Without Embedding) и использующие современные модели машинного обучения для создания заполненных контейнеров на основе векторов скрываемых данных [16, 17]. Фактически данные алгоритмы не реализуют классических операций модификации или встраивания данных в контейнер, не маскируют присутствие полезного сигнала под «естественными» шумами, а лишь формируют синтетические заполненные контейнеры-изображения, из которых сообщение может быть извлечено обученной сетью-экстрактором. Заполненные контейнеры формируются с помощью специально обученных глубоких свёрточных генеративно состязательных сетей. Подобные алгоритмы показывают хорошие результаты в части противодействия современным статистическим и обучаемым методам стегоанализа. Несмотря на новизну и общую перспективность данной группы алгоритмов, на практике существуют определенные ограничения, связанные с необходимостью обучения, хранения и передачи достаточно больших моделей и сложностями с использованием имеющихся контейнеров.

В данной работе рассматривается вариант развития ранее предложенного в [18] алгоритма скрытия данных в цифровые изображения, позволяющего встраивать сообщения, длина которых существенно превышает число модифицируемых элементов носителя, что позволяет повысить ПС при сохранении искажений контейнера на низком уровне. Алгоритм предусматривает разбиение контейнера-изображения на непересекающиеся блоки с поиском для каждого из них такого минимально искажённого представления, которое обеспечивает корректное извлечение фрагмента сообщения – слова заданной разрядности. Для снижения визуальной и статистической заметности факта скрытия разрядность каждого встраиваемого слова адаптируется с учётом характера внутреннего наполнения блока. В более шумные блоки встраиваются слова большей длины, а в блоки с однородным содержимым – слова меньшей длины. Процедура извлечения скрытых данных предполагает использование т.н. функции «свёртки» H , примеряемой к блокам пикселей и преобразующей входные данные произвольной длины в значения фиксированной длины (слова сообщения). Используемая в алгоритме функция H должна отвечать следующим требованиям:

– высокая скорость вычисления (с увеличением разрядности встраиваемых слов количество вызовов функции H при поиске подходящих вариантов искажения блока возрастает экспоненциально);

– равномерное распределение значений на выходе функции H , лавинный эффект и минимизация частоты коллизий.

В качестве функции H, обеспечивающей требуемое преобразование входных данных, можно рассматривать криптографические и некриптографические хеш-функции или циклические избыточные ко- ды. Криптографические хеш-функции были исключены из рассмотрения по причине избыточности для решаемой задачи как по времени работы, так и по разрядности формируемых ими кодов (≥ 128 бит), существенно превышающей обычную разрядность скрываемых слов сообщения (от 4 до 16 бит). Циклические избыточные коды характеризуются достаточно высоким быстродействием, но не всегда обеспечивают равномерность данных на выходе и приемлемую вероятность коллизий. В свою очередь, некриптографические хеш-функции, используемые в структурах данных для построения хеш-таблиц, характеризуются высоким быстродействием и хорошими статистическими свойствами формируемых выходных значений, поэтому при реализации стегоалгоритма предпочтение было отдано одной из наиболее производительных, обеспечивающих хорошую случайность выхода, мощный лавинный эффект и высокую устойчивость к коллизиям функции Murmur3 [19].

Отдельное внимание при разработке стегоалго-ритма было уделено вопросам мультиплексирования скрытых каналов. В работе рассмотрен вариант создания пары скрытых каналов, формируемых одновременно с использованием одного и того же подмножества элементов контейнера, позволяющих в несколько раз увеличить фактическую ПС алгоритма без необходимости внесения в блоки контейнера дополнительных существенных искажений. В качестве контейнеров рассматривались цветные изображения в модели RGB. В качестве встраиваемых сообщений рассматривались обычные бинарные файлы.

Алгоритм встраивания данных

Укрупнённая блок-схема алгоритма встраивания данных приведена на рис. 1. Она включает следующие шаги.

Шаг 1 . Загрузка файла-сообщения M и изображения-контейнера I размером W × H пикселей. Задание основных параметров встраивания, включающих размер обрабатываемых блоков ( w × h пикселей), компоненты стеганографического ключа, включающие параметры для инициализации начального состояния генераторов псевдослучайных числовых последовательностей (ГПСЧП), используемых для определения порядка обхода блоков I и для рандомизации встраиваемых слов. Разбиение контейнера на непересекаю-щиеся блоки b i е I , b i П b j = 0 , V i + j , i , j = 1,(W ■ H )/( w ■ h ).

Шаг 2 . Добавление целочисленного значения длины сообщения L M в его начало.

Шаг 3. Выбор в соответствии с ГПСЧП-1 на I очередного блока biеI и оценка его гладкости с целью определения оптимальной длины скрываемого в блок слова. Внесение при стегоскрытии сколь бы то ни было значимых искажений в гладкие блоки контейнера негативно отражается на визуальной и статистической заметности факта скрытия. В то же время шумные блоки кадра допускают потенциально бо́ льшие искажения, которые с меньшей вероятностью могут быть обнаружены при стегоанализе. В общем случае гладкость изображения можно рассматривать как функцию цветовых градиентов. В качестве параметра гладкости блока использовалось среднее значение дисперсий, вычисленных для модулей градиента блока в каждом его канале di= 3 Е ch=R,G, BD I grad ( bi. ch )).

Эмпирическим путем была предложена следующая шкала «гладкости», определяющая разрядность n встраиваемых и извлекаемых из блоков контейнера слов:

0, d <  0,15, n = 0;

• 1,    0,15 < d i < 0,3, n = 4;

C i   ' 2, 0,3 <  d i < 2, n = 8;

• 3,    2 <  d i < 7, n = 12;

• 4,    d , -> 7, n = 16.

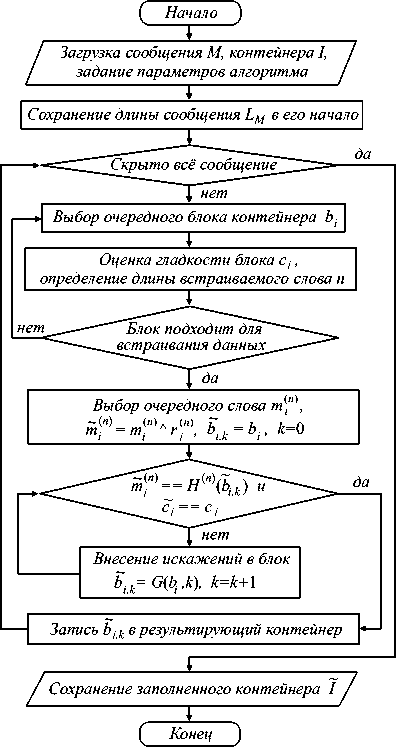
Рис. 1. Обобщённая схема работы алгоритма встраивания данных

Пример разметки блоков изображения «Lena» в соответствии с предложенной шкалой «гладкости» приведён на рис. 2 б .

Рис. 2. Исходное (а) и размеченное по уровню гладкости блоков (б) изображение «Lena»

При сохранении размеров блока и увеличении разрядности скрываемых слов будет увеличиваться вероятность искажений блока как по числу модифицируемых элементов, так и по амплитуде вносимых искажений. Отметим, что уменьшение разрядности встраиваемых слов в первую очередь оправдано при работе с небольшими блоками ( w < 4, h <  4,). Для блоков большей размерности количество получаемых на шаге 5 алгоритма модифицированных вариантов блока с малым уровнем искажений будет достаточно большим, чтобы выбрать необходимый вариант, обеспечивающий извлечение данных.

Шаг 4 . Выбор очередного n -битного слова m in ⁾ е M и его рандомизация сложением по модулю 2 со значением r_i ^{( n )} , формируемым на выходе ГПСЧП-2, m in ) = m in ) e Г n ) .

Шаг 5 . В цикле поиск подходящего варианта искажения блока b i,k такого, что

H ⁽ n) ( bX k ) = m (n ), || b - b i, k | |^ min и C i = C i . (1) Т.е. совпадение результата вычисления некриптографической хеш-функции H ^{( n )} от искажённого блока b ,k обеспечивает возможность корректного извлечения слова imin) при условии сохранения прежнего уровня «гладкости» блока. Для модификации элементов b применяется функция G вида

• b , k = G ( b, k ) =

= (b (1) + V1,k, b (2) + V2,k,^,b (Lb) + VLb,k), которая в зависимости от текущего значения переменной счётчика k добавляет к значениям цветов пикселей блока элементы вектора Vk =(vj,k,•••, VLb,k)T, где Vj,k, j = 1, Lb могут принимать значения {0, ±1, ±2,^,±X}, X - максимальное значение, добавляемое к значению цвета пикселя (обычно Х< 3), Lb = 3-w■ h - число доступных для модификации элементов блока для полноцветных контейнеров. Векторы Vk, k = 1, K формируются таким образом, чтобы при малых k количество и уровень вносимых изменений в b были минимальными, при этом в первую очередь затрагиваются пиксели в синем цветовом канале, потом в красном и зелёном. С увеличением k число одновременно модифицируемых коэффициентов в b , а также абсолютные значения приращений Vj,k постепенно увеличиваются.

После того как найдена подходящая модификация b ,k , она записывается в результирующий контейнер. Если просмотрены не все слова из M , выполняется переход к шагу 2.

Шаг 6 . Сохранение заполненного контейнера Ĩ .

Если принять гипотезу о том, что на выходе функции H ^{( n )} формируются случайные последовательности значений с равномерным распределением, то теоретически для успешной работы алгоритма встраивания количество векторов V _k , определяемое числом возможных неповторяющихся комбинаций значений приращений, должно быть сопоставимо с 2 ⁿ . На практике с учётом возможных коллизий для некриптографических хеш-функций количество векторов V _k должно в несколько раз превосходить размерности пространства решений 2 ⁿ .

Типичные гистограммы распределения числа итераций искажений блоков при встраивании слов разрядностью 8 и 16 бит приведены на рис. 3. В зависимости от используемой функции H , а именно от вероятности коллизий и стохастичности её выхода, гистограммы могут несколько отличаться. Для функции Murmur3 средние и медианные значения числа итераций, необходимых для встраивания 4-битных слов, составили 14 и 9, для 8-битных – 254 и 175, для 12битных – 4082 и 2827, для 16-битных – 67280 и 44826 соответственно.

Общее число K векторов приращений Vk зависит от размера модифицируемого блока, а также от максимального значения искажения цвета одного элемента X, заданного максимального числа одновременно искажаемых элементов и от значений, на которые они искажаются. Для оценки общего количества возможных комбинаций искажений можно использовать формулы комбинаторики – число сочетаний и/или размещений без повторений, применяемых для подсчёта различных вариантов искажения. Так, для блока размером 3*3 для Х< 2 и количестве одновременно модифицируемых значений яркости в b ,k не более трех K = 157824. Для блока размером 5×5 и аналогичных значений максимального уровня искажений и числа одновременно модифицируемых элементов K = 3556000. Для рассматриваемых в данной работе значений разрядности скрываемых слов 4 ≤ n ≤ 16 количество формируемых вариантов bi,k с малыми относительными искажениями оказывается достаточным для выполнения (1) даже для блоков малого размера. С увеличением размеров блока естественным образом увеличивается число возможных комбинаций вносимых искажений и, соответственно, необходимый результат (1) можно получить для комбинаций, соответствующих минимальным по уровню и числу подвергшихся модификации элементов, что позволяет встраивать слова, длина которых в битовом представлении существенно больше числа модифицируемых элементов блока.

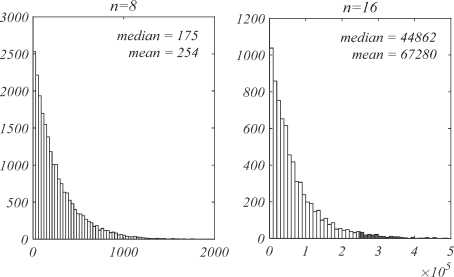
Рис. 3. Гистограммы распределения числа итераций искажений блоков при встраивании слов разрядностью 8 и 16 бит

Также стоит отметить, что на шаге 1 алгоритма встраивания возможен вариант формирования блоков из пикселей, выбранных в псевдослучайном порядке равномерно по всему контейнеру, что потенциально позволяет усложнить процедуру стегоанализа. Однако вследствие некоррелированности добавляемых в блоки пикселей из разных участков кадра количество сформированных блоков, имеющих малую гладкость и предполагающих встраивание слов большей разрядности, будет существенно выше, чем при формировании блоков из смежных пикселей, что негативным образом отразится на уровне искажения заполненных контейнеров. Поэтому при формировании содержимого блоков лучше рассматривать смежные пиксели, а форма блоков и порядок их обхода на кадре могут дополнительно рандомизироваться с использованием ГПСЧП.

Алгоритм извлечения данных

Укрупнённая блок-схема алгоритма извлечения данных приведена на рис. 4. Данный алгоритм не требует наличия исходного незаполненного контейнера, отличается вычислительной простотой и включает следующие шаги.

Шаг 1 . Загрузка заполненного контейнера Ĩ , задание основных параметров алгоритма, включающих размер блоков и начальные состояния используемых ГПСЧП .

Шаг 2 . Выбор в соответствии с ГПСЧП-1 на Ĩ очередного блока b i .

Шаг 3 . Оценка гладкости блока b i и определение длины извлекаемого слова n . Если блок гладкий ( c i =0), то он пропускается и осуществляется возврат к шагу 2.

Шаг 4 . Извлечение очередного слова путём вычисления некриптографической хеш-функции от блока тт (n ) = H ⁽ n ) ( b). Декодирование исходного значения слова путём его сложения по модулю два с выходом ГПСЧП-2 m tn ) = тт (n ) © r^ n ) .

Если длина сообщения M не сформирована, то m ^{( n )} записывается в соответствующую целочисленную переменную L M , иначе m ^{( n )} добавляется в результирующее сообщение M . Если число извлечённых байт меньше L M , выполняется переход к шагу 2.

Шаг 5 . Сохранение извлечённого сообщения M .

В решаемой задаче используемые при извлечении сообщений в качестве H ^{( n )} некриптографические хеши не являются инъективными и допускается появление коллизий, когда для блока b существуют различные его модификации b ,p ≠ b ,q , для которых H ^{( n )} ( b ,p ) = H ^{( n )} ( b ,q ). Наличие коллизий отражается на увеличении общего числа итераций искажения блоков контейнера, а значит, и времени работы алгоритма при работе в режиме поиска первой подходящей модификации блока (1). С другой стороны, наличие коллизий позволяет реализовать процедуру отбора из множества искажённых представлений блоков, обеспечивающих извлечение скрытых слов, таких вариантов, которые можно рассматривать в качестве прообразов для H ^{( v )} при извлечении v -битных слов в режиме мультиплексирования скрытых каналов.

Мультиплексирование скрытых каналов

Классические варианты мультиплексирования скрытых каналов, как правило, предполагают выделение в контейнере непересекающихся подмножеств модифицируемых элементов с последующим встраиванием в них информации, предназначенной для различных пользователей [18]. Описанные ниже принципы встраивания и извлечения информации могут быть использованы для организации нескольких скрытых каналов в рамках одного контейнера, предназначенных для скрытия различных сообщений, но , в отличие от классических вариантов мультиплексирования, работающих на одном и том же подмножестве элементов носителя.

Рассмотрим алгоритм мультиплексирования на примере создания в контейнере-изображении двух скрытых каналов CM и CS, используемых для передачи независимых сообщений M и S. Для простоты изложения рассмотрим алгоритм встраивания без адаптации длин скрываемых слов под гладкость каждого блока – будем считать, что во все пригодные для встраивания данных блоки контейнера I скрываются n-битные слова из M, а в пары различных блоков – v- битные слова из S. M = m(") || m2") ||..mNM , NM - число n-битных слов, составляющих скрываемое сообщение M. S = S1(v) || s2v) || ... sNS , NS - число v-битных слов, составляющих сообщение S.

Укрупнённая блок-схема алгоритма приведена на рис. 5. Она включает следующие шаги.

Шаг 1 . Загрузка сообщений M и S . Добавление целочисленных значений длин каждого сообщения в его начало. Задание основных параметров алгоритма, включающих размер обрабатываемых блоков, разрядность слов n и v , компоненты стеганографических ключей, включающие параметры для инициализации используемых ГПСЧП, рандомизирующих встраиваемые слова, а также определяющие порядок обхода блоков при встраивании M и S .

Шаг 2 . Выбор на I очередного блока b i , оценка его гладкости c i (если c i =0 – пропуск блока и переход в начало шага 2). Выбор очередного n -битного слова m in ) e M и его рандомизация m iⁿ ) = m iⁿ ) ® r^{( n} ) , r ⁿ ) - n -битное значение на выходе ГПСЧП-1.

Шаг 3 . Вычисление множества различных вариантов искажений блока b i B i = {b i ,1,... b_i , _Ni }, таких, что

(~   \        , x                              ------- bi,k) = m(n), Ci*0, Vk = 1,Ni.                 (3)

В терминологии криптографии элементы B i являются коллизиями для функции H ^{( n )} ( N i – число коллизий) и каждый из b i , k обеспечивает корректное извлечение слова m i" ) . Для модификации элементов b i применяется функция G . Если просмотрены не все слова из M , выполняется переход к шагу 2.

Шаг 4 . Выбор очередного v -битного слова s ^{( v} ) e S и его рандомизация s ,^v ) = s (^v ) ® r/ ^v ) , r/ ^v ) - v -битное значение на выходе ГПСЧП-2.

Шаг 5. Согласно ГПСЧП-3 выбор очередной пары модифицировавшихся блоков bi, bj. Поиск в сформированных на шаге 3 множествах вариантов искажений Bi и Bj элементов, для которых справедливо slv) = H(v) (b,.p Pj,q ) ,

II b - b > i,p 1 1 ^ min , || b j - b ) j,q 11 ^ min,

где || – операция конкатенации блоков (на уровне байтовых массивов), H ^{( v )} – некриптографическая хеш-функция с выходом длиной v -бит. Запись содержимого модифицированных блоков b i,p , b j,q на соответствующие позиции в результирующем контейнере Ĩ . Для обеспечения возможности встраивания и извлечения v -битных слов s^ ^v ) необходимо, чтобы число различных пар искажённых блоков b i , b j в (4), оцениваемое как произведение мощностей множеств B i и B j , было не меньше, чем 2 ^v (на практике с учётом возможных коллизий в несколько раз больше).

Переход к шагу 4, если l< N S , т.е. встроены не все слова из S .

Шаг 6. Если остались модифицировавшиеся на шаге 3, но не использованные для встраивания S бло- ки, из соответствующих им множеств Bi осуществляется выбор и запись в результирующий контейнер искажённых представлений блоков bi,p, минимально отличающихся от исходных ||bi- bip|| ^ min.

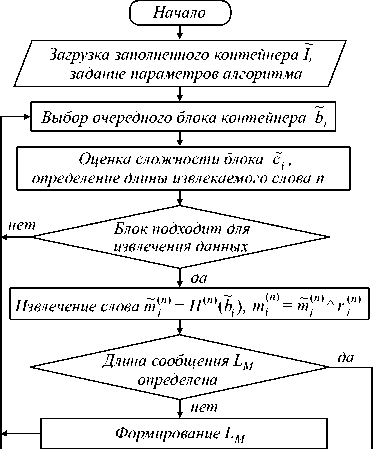
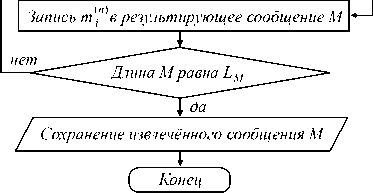
Рис. 4. Обобщённая схема работы алгоритма извлечения данных

Шаг 7 . Сохранение заполненного контейнера Ĩ .

В результате формируется заполненный контейнер Ĩ с парой скрытых каналов передачи информации C M и C S . Формирование данных каналов реализуется одновременно. В общем случае соотношение между размерами сообщений M и S может быть произвольным: | M | > | S |, | M | < | S |, | M | = | S |, все зависит от выбранной разрядности скрываемых слов каждого сообщения. Например, если n =4, а v = 16 и для скрытия используются все подходящие блоки контейнера, то | S | =2| M |. Соотношение между числом модифицируемых блоков контейнера подчиняется неравенству N_S <  N_M / 2.

В табл. 1 приводятся усреднённые по кадрам тестовой выборки значения частоты коллизий, формируемых для блоков заданного размера при встраивании в них n-битных слов. Каждая из коллизий обеспечивает корректное извлечение n-битного слова, но также характеризуется различным уровнем искажения соответствующего ей блока. С использованием данных из табл. 1 можно оценить примерную размерность пространства решений для задачи встраивания слов различной разрядности из сообщения S. Так, для блока размером 3×3 пикселя, n =8, максимальной амплитуды вносимых искажений X = 1 и максимальным числом одновременно искажаемых пикселей блока Ncorr ≤ 4 среднее число комбинаций пар искажённых представлений блока составит (2575)2, что более чем достаточно для встраивания слова sl(v) разрядностью 16 бит.

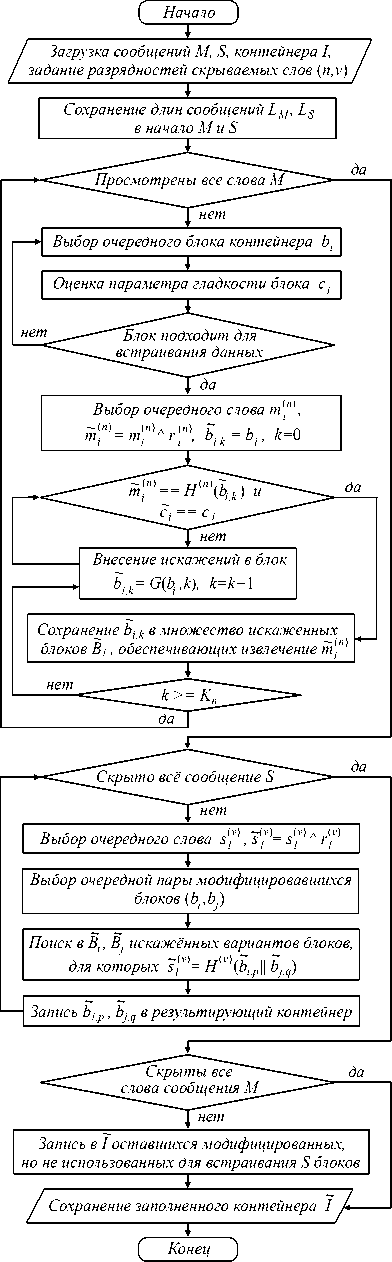
Рис. 5. Обобщённая схема алгоритма встраивания данных при создании двух скрытых каналов

Табл. 1. Среднее число искажённых вариантов блока, каждый из которых обеспечивает корректное извлечение n-битного слова

Размер и параметры искажения блока	n = 4	n =8	n =12	n =16
3×3, λ =1, N corr ≤ 3	1503	88	7	0,6
3×3, λ≤ 2, N corr ≤ 3	8352	526	34	3
3×3, λ =1, N corr ≤ 4	39381	2575	167	14
4×4, λ =1, N corr ≤ 3	8852	536	36	2
4×4, λ≤ 2, N corr ≤ 3	47405	3072	192	11
4×4, λ =1, N corr ≤ 4	480102	30896	1867	146
5×5, λ =1, N corr ≤ 3	34446	2 068	121	7
5×5, λ≤ 2, N corr ≤ 3	184329	11594	719	42
5×5, λ =1, N corr ≤ 4	3166088	197318	12328	748

Алгоритм извлечения сообщения из канала C M будет аналогичен представленному на рис. 4 с той разницей, что по результатам оценки гладкости блоков не производится определение разрядности извлекаемых слов. Если алгоритм скрытия с мультиплексированием каналов выполнялся с адаптацией длин встраиваемых слов, то схема извлечения данных из C M будет идентична представленной на рис. 4.

Алгоритм извлечения сообщения из канала C S включает следующие шаги.

Шаг 1 . Загрузка заполненного контейнера Ĩ .

Шаг 2 . Согласно ГПСЧП-3 выбор на Ĩ очередной пары блоков b i , b j , оценка их гладкости (гладкие блоки пропускаются, и выполняется переход в начало шага 2).

Шаг 3 . Извлечение и декодирование слова s lv) = H ( v ) ( b || b j ), s |v ) = s^lv ) ® r/ v ) . Если длина сообщения S не сформирована, запись s_l ^{( v )} в соответствующую целочисленную переменную L S . Иначе запись s_l ^{( v )} в результирующее сообщение S .

Если число извлечённых байт меньше L S , переход к шагу 2.

Шаг 4 . Сохранение сообщения S .

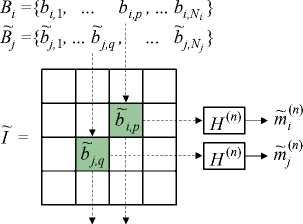
Схематичная графическая интерпретация операций встраивания/извлечения данных из первого и второго скрытых каналов приведена на рис. 6.

~

~

~

~

( v )

~

~

~

H ( v )

( b j, q || b i, p )

s l

Рис. 6. Пример выбора искажённых блоков, обеспечивающих извлечения данных из первого и второго скрытых каналов

На рис. 7 приведён пример исходных и модифицированных в режиме мультиплексирования скрытых каналов блоков контейнера при встраивании пары слов длиной 8 бит в CM и одного 8-битного слова в CS. В ка- честве H (8) использовалась некриптографическая хеш-функция Murmur3 c финализацией выхода по разрядности встраиваемых слов (seed = 135), λ≤ 2, Ncorr ≤ 3.

В общем случае каналы C M и C S могут использоваться для скрытной передачи данных любого характера, предназначенных различным абонентам. Особенность формирования скрытых каналов на основе одного и того же подмножества элементов контейнера допускает использование C M как второстепенного несекретного канала, маскирующего наличие канала C S , содержащего конфиденциальную информацию. В классической «проблеме заключённых» или в задаче о взаимодействующих агентах при обнаружении скрытого канала обмена, прямые его участники Алиса и/или Боб в условиях непреодолимых обстоятельств по требованию третьей стороны (охранника Вилли) теоретически могут раскрыть скрытно передаваемое «несекретное» сообщение M , объяснив соответствующие искажения в контейнере внесением в него конкретных элементов M в процедуре стеганографического встраивания. Естественно, что при этом не должен разглашаться тот факт, что эти же самые искажения вносились в контейнер и для встраивания второго «секретного» сообщения S . Используя предложенные принципы создания каналов C M , C S и зная принципы работы алгоритма встраивания/извлечения данных, при детальном анализе заполненного контейнера не возникает расхождений в числе модифицированных блоков и числе скрытых слов сообщения M , что исключает или минимизирует подозрения о существовании S .

b i	b i	b j	b j
40 41 93	40 41 93	65 45 40	65 45 40
R 40 79 109	39 79 109	R 59 47 55	59 47 54
55 106 112	55 106 112	55 49 87	55 49 87
30 36 103	30 36 103	51 32 30	51 32 30
G 30 79 119	30 79 119	G 43 33 48	43 33 48
48 110 119	48 110 119	41 39 87	40 39 87
34 38 108	34 38 108	47 35 34	47 35 34
B 34 81 134	34 81 134	B 42 36 53	42 36 53
53 116 135	53 117 135	40 42 99	40 42 99

m ⁽ i ^{8 )} = 1011 1110     m ⁽ j ^{8 )} = 1000 0111

s ⁽ _l ⁸⁾ = 0011 0110

Рис. 7. Пример пары искажённых блоков b i , b j , обеспечивающих извлечение тройки слов m_i ⁽⁸⁾ ,m ⁽ _j ⁸⁾ , s_l ⁽⁸⁾

Результаты экспериментальных исследований и их обсуждение

Экспериментальный анализ алгоритма стегоскры-тия проводился в части оценки зависимостей среднего числа модифицируемых элементов и уровня их искажений в блоках различного размера от длин встраиваемых в данные блоки слов, итогового уровня искажений стегоконтейнеров, а также времени, затра- чиваемого алгоритмом на создание заполненных контейнеров. Тестирование проводилось на выборке из 50 полноцветных изображений в модели RGB из базы данных PPG-LIRMM-COLOR [20]. В базе представлены кадры размером 512×512 пикселей, хранящиеся в формате bmp. В качестве скрываемых сообщений рассматривались псевдослучайные последовательности чисел требуемой длины, которые формировались алгоритмом MT19937.

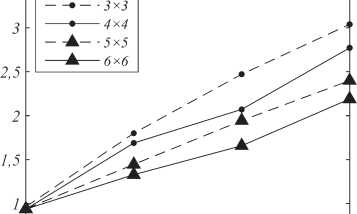
На рис. 8 приводятся зависимости среднего числа модифицируемых значений в блоках различного размера от разрядности встраиваемых в данные блоки слов. С уменьшением размеров блоков и увеличением длины скрываемых слов естественным образом увеличивается число потенциально модифицируемых элементов. Так, для встраивания 16-битного слова в блок размером 3×3 в среднем необходимо модифицировать три элемента. Для встраивания 8-битного слова в блок того же размера в среднем необходимо модифицировать менее двух элементов.

Среднее число модифицируемых элементов в блоке

3,5 \                             I ---------------------------1------------------

0,5'-----------------------1-----------------------1-----------------------

4            8            12           16

Разрядность скрываемого слова

Рис. 8. Зависимость среднего числа модифицируемых элементов блока от разрядности скрываемых слов

На рис. 9 приводятся зависимости среднего значения амплитуды искажения модифицируемых элементов в блоках от разрядности встраиваемых в них слов. Амплитуда искажений определяется приращениями λ в функции искажения и измеряется в уровнях яркости /цветности. Даже для блоков малого размера средний уровень искажения подмножества модифицируемых при встраивании элементов не превышает 1,15. Для встраиваемых слов разрядностью 8 бит средний уровень искажений примерно равен 1 для всех рассмотренных размерностей блоков.

Приведённые на рис. 8, 9 зависимости получены для стегоконтейнеров, сформированных без мультиплексирования скрытых каналов. В режиме создания двух каналов для малых разрядностей скрываемых слов n =4 и v ≤ 8 значения среднего числа модифицируемых элементов, а также средний уровень вносимых искажений будут сопоставимы с приведёнными выше. Для n ≥ 8 и v ≥ 8 минимальное необходимое для скрытия M и S число модифицируемых элементов и ам- плитуда модификации в среднем оказываются несколько больше . Насколько – зависит от отношения разрядностей скрываемых слов, размеров обрабатываемых блоков и заданных максимальных значений λ и Ncorr.

Средний уровень искажения модифицируемых

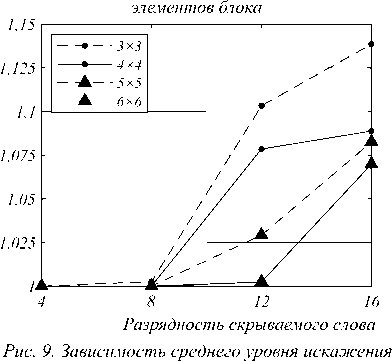
модифицируемых элементов блока от разрядности скрываемых слов

Для оценки степени искажения заполненных контейнеров рассматривались традиционные метрики – пиковое отношение сигнала к шуму (PSNR), индекс структурного сходства (SSIM) и максимальная абсолютная ошибка (MAE). В табл. 2 представлены результаты оценки данных показателей для рассматриваемого в работе алгоритма, использующего некриптографические хеш-функции для извлечения скрытых данных (обозначен аббревиатурой АНХ) с параметрами размера блока 4×4, λ≤ 2, N corr ≤ 3, а также для пары современных алгоритмов адаптивной пространственной стеганографии WOW и S-UNIWARD. Для всех алгоритмов реализовывалось встраивание в RGB-изображения с фактическим одинаковым объёмом полезной нагрузки α , определяемым средним количеством встраиваемых бит стегосообщения, приходящихся на пиксель контейнера. При оценке объёма полезной нагрузки факт пропуска блоков с малой стохастичностью в выбранных для сравнения алгоритмах также учитывался. Для всех α предложенный алгоритм показал меньшие искажения, чем WOW и S-UNIWARD, по показателям PSNR и SSIM, что объясняется используемыми принципами встраивания, позволяющими скрывать больше бит, чем число фактически модифицируемых бит носителя. В то же время при α >0,5 в маркированных предложенным алгоритмом контейнерах встречаются отдельные блоки с бо_́ льшим уровнем абсолютных искажений, чем в контейнерах, сформированных алгоритмами WOW и S-UNIWARD.

В табл. 3 приведены усреднённые по тестовой выборке значения времени (в секундах) создания заполненного полноцветного контейнера размером 512×512 пикселей для различных вариантов алгоритма стегоскрытия, предусматривающих фиксирован- ную или автоматически определяемую разрядность встраиваемых слов. При задании фиксированной разрядности скрытие n-битных слов происходило во все блоки размером 4×4 пикселя, «гладкость» которых превышала 1. Контейнеры создавались из расчёта 100% их заполнения скрытой информацией. Результаты получены для двух вариантов функции H – некриптографической хеш-функции Murmur3 с финали-зацией длины её выхода под размер слова, а также для быстрых табличных реализаций циклических избыточных кодов CRC-8 и CRC16-CITT, используемых при скрытии слов разрядностью 4, 8 и 12, 16 бит соответственно.

Табл. 2. Результаты сравнения алгоритмов стегоскрытия по показателям искажения заполненных контейнеров

Наименование	PSNR	SSIM	MAE
алгоритма	α =0,1
WOW	66,433	0,9999	1
S-UNIWARD	66,778	0,9999	1
АНХ	69,846	0,9999	1
	α =0,5
WOW	59,319	0,9996	1
S-UNIWARD	59,032	0,9994	1
АНХ	62,988	0,9999	1
	α =1
WOW	55,348	0,9986	1
S-UNIWARD	54,796	0,9973	1
АНХ	59,959	0,9997	2

Табл. 3. Среднее время (в секундах) создания заполненного контейнера размером 512×512 пикселей при 100 % его заполнении скрытой информацией

Разрядность встраиваемых слов	Тип функции H
	Murmur3	CRC-8, CRC-16-CCITT
n = 4	0,018	0,019
n = 8	0,041	0,075
n =12	0,375	1,896
n =16	3,386	27,303
Определяется автоматически	0,759	5,732

В таблице представлены результаты для распараллеленного варианта алгоритма скрытия (многопоточная реализация на языке C++, компилятор MinGW gcc-7.3.0, CPU Intel Core i5-10400 2.90ГГц, 16Гб ОЗУ). Несмотря на достаточно большое число итераций искажения блоков при встраивании в них 16битных слов, общее время создания заполненного контейнера не превышает 3,5 секунд для используемой по умолчанию некриптографической хеш-функции Murmur3. При аналогичных условиях реализация алгоритма с циклическими избыточными кодами оказалась в 8 раз медленнее. При меньших разрядностях встраиваемых слов, а также в варианте алгоритма с адаптацией длин скрываемых слов под гладкость блоков среднее время работы алгоритма встраивания с функцией Murmur3 составило менее 1 секунды на кадр, что в среднем в 1,8 – 7,5 раз быстрее, чем для реализации с CRC.

Усреднённые значения времени создания контейнеров для алгоритма, работающего в режиме мультиплексирования скрытых каналов, приведены в табл. 4.

Для ускорения работы алгоритма в режиме создания пары скрытых каналов полные множества искажённых вариантов блоков B i и B j (см. табл. 1) не формируются. Добавление подходящих искажённых вариантов блоков в соответствующие множества реализуется последовательно с одновременной проверкой выполнения условия (4) для всех пар блоков, которые можно сформировать с текущим добавляемым искажённым блоком. При формировании возможных пар множества B i и B j просматриваются сначала. Если найдена подходящая пара блоков, то их содержимое сохраняется в результирующий контейнер и алгоритм переходит к встраиванию следующей тройки слов. Таким образом удаётся существенно сократить время работы алгоритма и обеспечить минимальные искажения итогового контейнера.

Табл. 4. Среднее время (в секундах) создания заполненного контейнера размером 512×512 пикселей при 100 % его заполнении скрытой информацией в режиме мультиплексирования скрытых каналов

Разрядность встраиваемых слов	Размер блоков 4×4, λ≤ 2, N corr ≤ 4
n =4, v =4	0,637
n =4, v =8	0,828
n =4, v =12	1,470
n =4, v =16	4,055
n =8, v = = =4	0,607
n =8, v =8	1,785
n =8, v =12	7,621
n =8, v =16	28,869

Подробное рассмотрение вопросов стеганографической стойкости предложенного алгоритма выходило за рамки данной работы. Тем не менее с использованием глубокой свёрточной модели Yedrouj-Net [21] было проведено тестирование в части сравнения стеганографической стойкости предложенного алгоритма (размер блока – 4×4, λ ≤ 2, Ncorr ≤ 3,) с алгоритмами WOW и S-UNIWARD для двух вариантов «загрузки» контейнеров α =0,1 и α = 1. Yedrouj-Net входит в число современных эффективных моделей, применяемых для стегоанализа в пространственном представлении контейнеров. Её архитектура предполагает использование шести свёрточных и трёх полносвязных слоев. В первых свёрточных слоях используются нелинейные активации в виде функций abs и trunk. При проведении тестирования использовалась база изображений PPG-LIRMM-COLOR. В ходе исследований для анализа каждого алгоритма скрытия при заданном значении объёма полезной нагрузки обучалась отдельная модель. Каждым алгоритмом формировалось по 2000 заполненных контейнеров. В качестве скрываемых данных рассматривался выход ГПСЧП. Тренировочные наборы включали по 1500 заполненных и соответствующих им исходных контейнеров, для ва- лидации и тестирования использовались по 250 оставшихся заполненных и соответствующих им исходных контейнеров, гиперпараметры задавались согласно [21]. При α =0,1 усреднённые значения точности детектирования факта стегоскрытия для всех алгоритмов оказались примерно одинаковы и составили 60% для предложенного алгоритма и WOW и 58 % для S-UNIWARD. При α = 1 наибольшая усредненная точность обнаружения в 94% была зафиксирована для предложенного алгоритма, в то время как для алгоритмов WOW и S-UNIWARD соответствующие значения составили 87 и 83 %. Отчасти меньшая устойчивость предложенного алгоритма к стегоана-лизу при увеличении объемов полезной нагрузки обуславливается бо́ льшим уровнем абсолютных искажений (MAE ≥ 2), вносимых в отдельные немногочисленные элементы контейнера, а также менее избирательным характером самого алгоритма выбора пикселей для модификации в рамках обрабатываемых блоков. Следует обратить внимание на то, что WOW и S-UNIWARD в первую очередь разрабатывались как алгоритмы, способные эффективно противодействовать стегоанализу. Подробное рассмотрение вопросов стеганографической стойкости предложенного алгоритма и проведение более масштабных его исследований планируется в следующей статье по данной тематике.

Заключение

Описанные в работе принципы встраива-ния/извлечения данных являются универсальными и могут применяться как в пространственном, так и в частотном представлении контейнеров различных форматов. Предложенный алгоритм не является робастным и предназначен для создания стегоконтейне-ров, не подвергающихся дополнительным искажениям. Алгоритм имеет настраиваемую ПС, зависящую от размеров искажаемых блоков, разрядности встраиваемых слов, характера содержимого самого контейнера, определяющего процент пропускаемых блоков или блоков, для которых длина встраиваемых слов автоматически уменьшается. На практике алгоритм способен обеспечить соотношение числа фактически модифицируемых бит контейнера к числу встраиваемых бит сообщения порядка 0,06 (для большинства классических стегоалгоритмов этот показатель находится на уровне от 0,5 и выше), что положительным образом отражается на минимизации итоговых искажений стегоконтейнеров.

Отличительной особенностью предложенного варианта мультиплексирования скрытых каналов является использование одного и того же подмножества элементов, подвергающихся одинаковым искажениям при встраивании различных сообщений.

Стоит отметить, что алгоритм встраивания очень хорошо подходит для распараллеливания. Все слова скрываемого сообщения могут встраиваться в соот- ветствующие им блоки кадра независимо друг от друга. В режиме мультиплексирования скрытых каналов зависимыми будут лишь пары одновременно искажаемых блоков.

В числе возможных направлений развития данного алгоритма можно отметить изучение возможностей использования GPU для ускорения вычислений при работе со словами разрядностью более 16 бит, а также подробное изучение вопросов устойчивости алгоритма к современным методам стегоанализа.