Адаптивный цифровой корректор амплитудно-частотных характеристик каналов

В ряде систем связи, в информационно-измерительных системах, в системах контроля и регулирования возникает необходимость построения корректоров АЧХ каналов, трактов передачи и т.д. [1]. Суть коррекции АЧХ канала состоит в том, что в силу различных явлений неравномерность АЧХ канала изменяется во времени и необходимо периодически компенсировать эту неравномерность, включив на выходе канала адаптивный корректор, АЧХ которого изменялась бы так, чтобы результирующая неравномерность АЧХ тракта канал-корректор оставалась неизменной с определенной погрешностью . Возможности цифровой обработки сигналов позволяют создавать такие адаптивные корректоры АЧХ каналов [2-3]. В технической литературе описаны методы расчета фильтров различного типа. В том числе с адаптивными характеристиками [4-10].

В данной статье приводится методика расчета и описание работы адаптивного цифрового корректора, в основу которого положен нерекурсивный цифровой фильтр порядка 2 k с симметричными коэффициентами b_n относительно центрального коэффициента фильтра b ₀. Структурная схема такого фильтра приведена на рис . 1. Порядок нерекурсивного фильтра 2 k определяется числом элементов задержки в схеме фильтра. Фазо-частотная характеристика этого фильтра линейная, а амплитудно-частотная характеристика описывается выражением [2]:

ВД =

к

^ С„ COS 2Л77Х

77=0

где         – частота, нормированная к часто те дискретизации Нормированную частоту x достаточно изменять от 0 до 0,5, дальше АЧХ циклически повторяется. Коэффициенты фильтра b0 и bn связаны с входящими в эту формулу коэффициентами Сп следующим образом:

Желаемую АЧХ фильтра F ( x ) в полосе пропускания можно задать равномерной F ( x ) = C , с определенным наклоном F ( x ) = Ax + B или рельефной в форме параболы

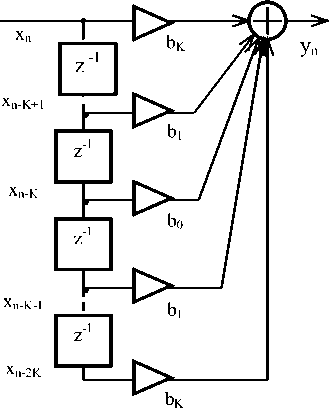
Рис. 1. Структурная схема нерекурсивного цифрового фильтра порядка 2 k с симметричными коэффициентами

Коэффициенты А, В и С определяют вид рельефности АЧХ фильтра в полосе пропускания и являются исходными данными для расчета коэффициентов b0 и bn фильтра, выполняющего функцию корректора АЧХ канала. Иначе гово- ря, коэффициенты b0 и bn являются параметрами адаптивного корректора АЧХ канала.

Расчет коэффициентов фильтра по заданной рельефности АЧХ в полосе пропускания

На рис. 2 приведены рельефные АЧХ фильтров четырех типов: фильтра нижних частот (ФНЧ), фильтра верхних частот (ФВЧ), полосового фильтра (ПФ) и режекторного фильтра (РФ). Здесь мы ограничимся расчетом только полосового фильтра (ПФ), то есть получим формулы для расчета его коэффициентов b ₀ и b_n , обеспечивающих рельефность АЧХ в полосе пропускания в форме параболы F(x) = Ax" + Bx + C , поскольку из параболы вытекают частные случаи: АЧХ с наклоном при А = 0 или равномерная АЧХ при A=B = O.

Они являются исходными данными для последующего расчета. Коэффициенты a ₁, b ₁, a ₂, b ₂ определяются по формулам:

. F(F,1) . ^^ 1         ^^ 1 ^ 31 x„i - x31 f(^2) (4) tz2 =------------- : , 1)^ — Q^X^-) s X32 — Xni где ^(F/l,?) ^^11.2 “*“ ^ ^1.2 "*" C – значения АЧХ полосового фильтра на нижней и верхней границах полосы пропускания. Тогда искомые коэффициенты b0 и bn фильтра определим по формуле рядов Фурье [1]:

0.5

b_n = jF(x) COS (2^77x)tZx.

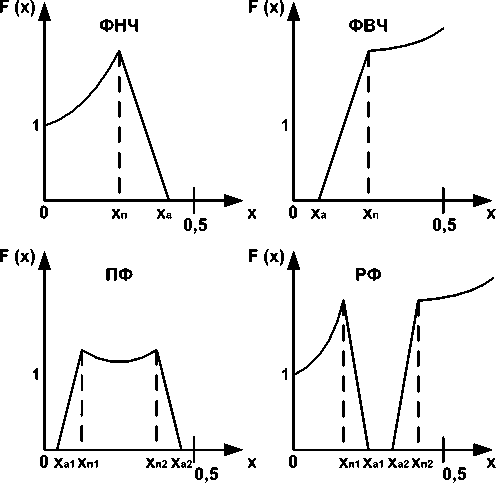
Рис. 2. Рельефные амплитудно-частотные характеристики фильтров четырех типов: ФНЧ, ФВЧ, ПФ и РФ

Подставим в эту формулу приведенное выше выражение для F ( x ), проинтегрируем ее по всем участкам изменения х в интервале от 0 до 0,5 и получим следующие формулы для расчета коэффициентов b ₀ и b_n фильтра-корректора АЧХ:

b0=-(x32-x3x) + B(x32-x^

2C(x_n2 - x_/d ) + F(x_nl )(x_nl - x₃₁) +       (6)

+ F(x„₂)(x₃₂ -x„₂);

,         0.5 . .      _                   _         .

b, =-----(a, (cosz^zx. - cos2^Mx,,) +

(Л72)

+ a₂ (cos 2ттх₁₁₂ - cos 2roix₃₁) +

+ S(cos 2ттх_п2 - cos 2raix_nX) + 2A^x_n2 COS2^77X_/|2 -х_л1 COS27Z77X_nl) +

+     (sin2^77X„, -sin2^77X„J).

2 mi

Аналитическое выражение F ( x ) для АЧХ полосового фильтра на всем участке изменения нормированной частоты х имеет вид

0;

axx + bx;

F(x) = <

Ax2 + Bx + C;

a2x + b2;

0;

0 < x < x31;

x3i <х<хи1;

x„i^

*я2 < -X < -^32 i x32 < x < 0,5;

где х_п1, х_п2, х_з1, х_з2 – нормирование границы полос пропускания и заграждения фильтра (см. рис. 2).

Здесь величина n изменяется от 1 до k. Отметим, что реальная АЧХ фильтра К(x) будет отличаться от желаемой, описываемой выражением F(x). И отличие это будет тем меньше, чем выше порядок фильтра. А порядок фильтра 2k однозначно определяет число гармоник k ряда Фурье, участвующих в формировании рельефной АЧХ полосового фильтра, изображенной на рис. 2.

В полученных формулах для расчета коэффициентов b₀ и b_n неизвестными являются коэффициенты, аппроксимирующие форму рельефности АЧХ фильтра. Опишем процедуру расчета этих коэффициентов.

Алгоритм расчета  коэффициентов, аппроксимирующих форму рельефности АЧХ фильтра

Для расчета коэффициентов А; В и С введем еще одну нормированную частоту:

x_n =0,5(x,„ + х„₂),                (8)

то есть х_п – это средняя частота полосового фильтра. Для придания корректору адаптивных свойств необходимо периодически измерять значения АЧХ канала W на трех частотах х_п1, х_п2 и х_п. Допустим, мы измерили эти значения АЧХ канала на трех частотах ^,,i); <х„₂), ЩхЛ В результате измерений оказалось, что они не равны между собой и отличаются от требуемого постоянного значения АЧХ канала, равного значению К. Тогда, зная измеренные величины ^(х„0; ^(х„₂), W(x„) и желая иметь одинаковое значение АЧХ канала на всех трех частотах равным К, определим необходимые значения АЧХ фильтра-корректора на этих трех частотах:

F(x.) =-------; F(xn1) =;

"^V W(x„J ^{V nJ} ^,,₂)

. к(9)

F^n^",^^ ^(х„)

Теперь составим систему из трех уравнений:

F(x_nX) = Ax^+Bx_nl+C;

F(xn2) — Axn2 + Bxn2 + C,

F(x„) = Ax; + Bx„ + C.

Неизвестными в этой системе линейных уравнений являются коэффициенты А; В и С. Решив эту систему уравнений относительно неизвестных, найдем искомые коэффициенты А; В и С, обеспечивающие необходимую форму рельефности фильтра-корректора АЧХ канала связи. Измерения величин ^X.x„O; ^(x„₂), W(x„) требуют определенного времени и дополнительных технических средств: генераторов, детекторов, измерительной техники. Для каждого конкретного случая выбирается тот или иной способ измерений. Периодичность измерения величин W(x_nV); W(x„A, W(x„) выбирается в зависимости от того, насколько быстро изменяются во времени характеристики канала связи.

Заключение

В статье получены формулы для расчета параметров и описание работы адаптивного цифрово- го корректора АЧХ канала, но не рассматриваются точностные характеристики адаптивного цифрового корректора АЧХ во всей полосе пропускания канала. Однако они могут быть однозначно определены из полученных в данной статье формул и расчетных соотношений. Если рельефность АЧХ в форме параболы, то есть в виде полинома второго порядка, окажется слишком грубой по точности аппроксимации АЧХ корректора для компенсации неравномерности АЧХ канала, тогда можно использовать для аппроксимации полиномы более высокого порядка. Но при этом усложняются формулы для расчета коэффициентов b0 и bn, а также усложняется алгоритм вычисления коэффициентов аппроксимирующего полинома.