Адаптивный метод последовательных уступок при решении задачи векторной оптимизации характеристик системы инженерноаэродромного обеспечения боевых действий авиации ВВС

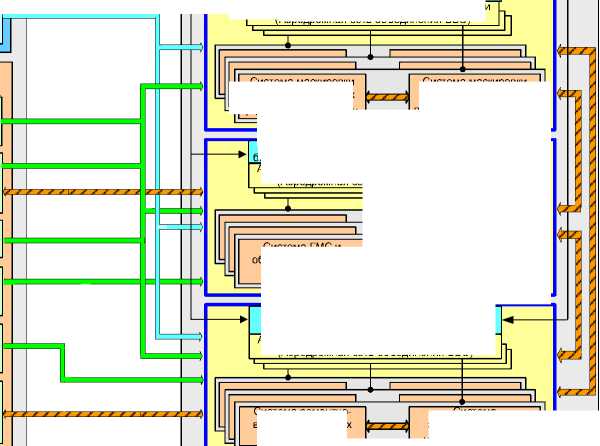
В результате проведения многоуровневой декомпозиции системы инженерно-аэродромного обеспечения (ИАэО) боевых действий авиации ВВС появилась возможность существенно упростить решение задач обоснования требований к характеристикам составляющих ее подсистем. Вариант функциональной декомпозиции системы ИАэО боевых действий авиации и связи между ее подсистемами и исходными данными по противнику и своим войскам изображены на рис. 1.

На рисунке 1 представлены два вида связей. Незаштрихованными линиями показаны связи характеристик исходных данных и своих войск, непосредственно влияющих на характеристики подсистем системы ИАэО, которые должны учитываться при оптимизации параметров этих подсистем. Заштрихованными линиями – связи характеристик исходных данных, которые

Исходные данные

Характеристики противника

X (X ,X ) ∈ Ω

2 2.1 2.2         X ₂

Система ИАэО боевых действий авиации на постоянных аэродромах ВВС X i ( G i , G 2 , G 3 , G 4 , G 5 , G 6 ) gQ x ,

Характеристики вариантов построения ударов СВН противника по аэродромам X 2.1

Обеспечение живучести базирования авиации

Маскировка аэродромов

Скоростное восстановление аэродромов

Система маскировки аэродромов

Аэродромы базирования группировки авиации (Аэродромная сеть объединения ВВС)

Характеристики конструкций для восстановления разрушенных аэродромных покрытий X 3.5

ТТХ и ВПХ базирующейся на аэродромах авиации X 3.3

ТТХ АСП, применяемых по объектам базирования группировки авиации X 2.2

Параметры производственных возможностей рем. органов системы восстановления АТ X 3.4

Параметры производственных возможностей ремонтных звеньев системы скоростного восстановления аэродромов X 3.6

Характеристики своих войск ^X3^(X3.1^,X3.2^,X3.3^,X3.4^,X3.5^,X3.6^{) ∈ Ω} X3 Характеристики боевых действий ИА и ЗС, прикрывающих объекты аэродромной сети X 3.1

Состав и конструктивнопланировочные параметры основных элементов аэродромов аэродромной сети X 3.2

Система эшелонирования и накопления РВМ G 6

Система ремонтновосстановительных сил и средств G5

Рис. 1. Вариант функциональной декомпозиции системы ИАэО боевых действий авиации ВВС

Система маскировки ВС на МС, защитных - укрытий ВС и ИМС G i

Система маскировки элементов летного поля (ВПП, РД, ГМС) G 2

Система обеспечения живучести базирования авиации на постоянных аэродромах Аэродромы базирования группировки авиации (Аэродромная сеть объединения ВВС) _____|

Система ГМС и обвалованных ИМС

G 3

Система защитных укрытий ВС G 4

Система скоростного восстановления аэродромов Аэродромы базирования группировки авиации (Аэродромная сеть объединения ВВС)

оказывают взаимообусловленное влияние друг на друга и поэтому должны оптимизироваться совместно.

Рассмотрим подсистемы, решающие наиболее важные задачи инженерно-аэродромного обеспечения боевых действий авиации на постоянных аэродромах ВВС. К таким подсистемам, характеристики которых необходимо оптимизировать, относятся подсистема маскировки аэродромов; подсистема обеспечения живучести базирования авиации; подсистема скоростного восстановления аэродромов в ходе боевых действий.

Декомпозиция системы ИАэО в данном варианте является в некоторой степени условной, так как между подсистемами остаются устойчивые связи, а характеристики каждой из них оказывают влияние на соответствующие характеристики другой подсистемы. Например, подсистема маскировки аэродромов и подсистема обеспечения живучести базирования авиации имеют общие силы и средства маскировки авиационной техники и элементов базирования (ГМС, обвалованных ИМС, защитных укрытий, зон рассредоточения). Так, при обосновании требований к характеристикам подсистемы живучести базирования авиации на постоянных аэродромах ВВС (кроме других прочих характеристик) обосновываются характеристики инженерно-маскировочных и ложных мероприятий базирования авиации, а также количественные и качественные параметры ИМС, ГМС и защитных укрытий ВС. Вместе с тем при обосновании характеристик подсистемы маскировки постоянных аэродромов ВВС также обосновываются требования к значениям характеристик указанных параметров системы.

При обосновании требований к характеристикам подсистемы скоростного восстановления аэродромов кроме характеристик, определяемых системой восстановления, устанавливаются требования к значениям характеристик инженерно-маскировочных и ложных мероприятий основных элементов летного поля аэродромов (ВПП, РД и МС), которые также являются варьируемыми параметрами системы маскировки аэродромов. Подсистема маскировки аэродромов оказывает влияние на объемы разрушения основных элементов летного поля (ВПП, РД, МС), восстанавливаемых подсистемой скоростного восстановления в ходе боевых действий, и поэтому их возможности по отношению друг к другу не должны быть избыточны и наоборот.

Характеристики системы обеспечения живучести базирования авиации должны быть «согласованы» с параметрами подсистемы скоростного восстановления аэродромов, исключая взаимную избыточность и наоборот и т.д.

Однако это не противоречит представленному на рис. 1 варианту декомпозиции, так как взаимосвязи подсистем могут быть учтены при задании требований к характеристикам каждой из них. Это осуществляется путем включения общих элементов в рассматриваемую подсистему и исключения их из взаимодействующих подсистем с дальнейшим учетом этого обстоятельства при разработке метода агрегирования подсистем в единую систему ИАэО боевых действий авиации.

Таким образом, окончательно в качестве рациональных характеристик системы ИАэО в целом выбирать полученные результаты решения частных оптимизационных задач нельзя. Это обусловлено тем, что в реальности предложенный вариант декомпозиции, хотя и учитывает максимально возможную автономность функционирования подсистем, однако не исключает ряд определенных устойчивых связей между ними. Элементы рассматриваемых подсистем, функционирующих в военное время, позволят предположить избыточность возможностей подсистем, поскольку часть их элементов может дублировать функции друг друга. Поэтому характеристики подсистем системы ИАэО должны быть соответствующим образом сбалансированы.

Следовательно, при анализе характеристик подсистем, полученных в результате решения частных задач, некоторые из них для различных подсистем окажутся избыточными при формировании характеристик системы ИАэО в целом.

Это обстоятельство можно пояснить с помощью алгебры множеств на основе построения диаграмм Венна. Построение диаграммы начинается с разбиения плоскости на 2 n ячеек с помощью n замкнутых линий, соответствующих различным множествам, элементами которых выступают числовые значения характеристик исследуемых подсистем системы инженерноаэродромного обеспечения боевых действий авиации на постоянных аэродромах ВВС и участвующих в данной совокупности соотношений. Особенностью этих диаграмм является то, что каждая последующая фигура, соответствующая определенному множеству характеристик, имеет одну и только одну общую область с каждой из ранее построенных фигур. Поскольку в рассмотренном варианте декомпозиции системы ИАэО выделено три подсистемы, имеет смысл рассматривать множества их характеристик A_b A ₂, A ₃. Символ Венна для n = 3, разбивающий плоскость на 8 ячеек, представлен на рис. 2.

На рисунке 2 множество А ] включает совокупность характеристик системы маскировки постоянных аэродромов ВВС, множество А ₂ - системы обеспечения живучести базиро-

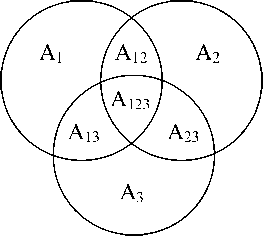
Рис. 2. Символ Венна при n - 3

вания авиации и А3 - системы скоростного восстановления аэродромов в ходе боевых дей- ТТ                                                                     Л     Л ПЛ ПЛ ствий. Получившиеся при пересечении множеств A], A2, A3 подмножества A123 - Ai 11A2MA3, А13 = А11А31А2, А23 = А21А31 А1 образуют множества характеристик подсистем, дублирующих друг друга, подмножество Л123 соответствует тройному перекрытию значений характеристик подсистем. Для исключения избыточности характеристик системы ИАэО в целом необходимо провести операцию объединения множеств, в результате которого получим множество В = U An, содержащее все характеристики системы инженерно-аэродромного обеспече-П = 1 ~                                                                                                                                           А ния боевых действий авиации. Следует заметить, что множества характеристик подсистем А], А2, Аз толерантны между собой, то есть А] т А2, А] т Аз, А2 т Аз, так как А I А * 0, А1 1 А3 * О, А21А3 * 0 соответственно. Пусть задано множество B - {B1, B2,.Bm}. Введем множество признаков P - {p1, p2,...pn} , каждый элемент которого характеризует принадлежность соответствующих характеристик из множества В подсистемам инженерно-аэродромного обеспечения и особенностям их функционирования.

Таким образом, каждому признаку p i e P соответствует некоторая совокупность характеристик из В , которые обозначаются этим признаком и образуют классы толерантности { K ₁, K ₂,. K L }. Различные классы толерантности могут содержать одинаковые элементы и, следовательно, являются пересекающимися множествами, а их объединение равно множеству В , то есть K ₁ U K j U^U K _L = B • В результате можно получить матрицу отношений 0 размерами m х n , элементы которой равны единице, то есть 0 _У = 1, если характеристика подсистемы b i , i e 1, m определяется признаком P j , j e 1, n , и 0 _y = 0 в противном случае. Так, для подсистемы маскировки аэродромов можно ограничиться признаком р 1 , для подсистемы обеспечения живучести базирования авиации признаком р₂ соответственно, для подсистемы скоростного восстановления аэродромов - признаком р₃ . В этом случае множество A ₁ - K ₁, A ₂ - K ₂, A ₃ - K ₃.

Разбиение множества на классы можно связать с отображением f : B ^ Э , ставящим элементам из В один и только один элемент из Э (множества частных значений эффективностей функционирования подсистем). Известно, что любое отображение f : B ^ Э порождает отношения эквивалентности на множестве В . Образы Э ; классов эквивалентности образуют в совокупности системы представителей на Э . Сказанное можно проиллюстрировать графически. На рисунке 3 представлено отображение f : B ^ Э , порождающее отношение эквивалентности на В .

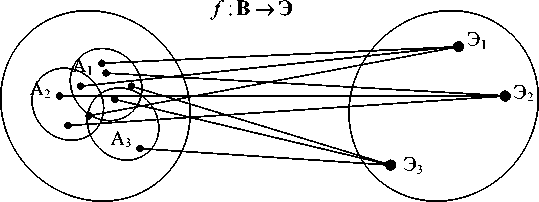
Рис. 3. Отображение f : B ^ Э

Аналогично строится отображение f₂ : B ^ C , где С - множество стоимостей подсистем системы инженерно-аэродромного обеспечения, таких что f , ( b i е A n ) = C n , n = 1,3.

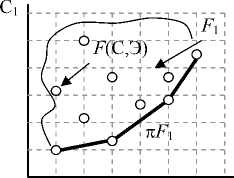
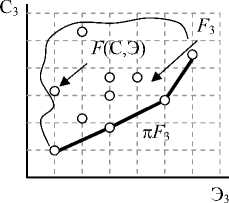
В результате решения частных оптимизационных задач при различных значениях частных показателей эффективности функционирования подсистем системы ИАэО Эn, n = 1,3 получаем совокупности оптимальных по Парето альтернатив. Это означает, что на мно- жестве возможных альтернатив построения подсистем системы ИАэО с характеристиками bi е An, n = 1,3, определены скалярные функции Cn (bi е An ) и Эп (bi е An ). При этом будем понимать, что альтернатива b-1 доминирует по Парето над альтернативой bi(2)bz(1)f b^), если С(bi-1^)^ С(b^) и Э(Ьу-1))> Э(b(2)) или хотя бы одно из неравенств является строгим. Полагая множество векторных оценок Fn,n = 1,3 в плоскости «стоимость-эффективность» вы-n пуклым, ограниченным и замкнутым, что не противоречит физике рассматриваемых яв- лений, можно провести графическую интерпретацию изложенного. На рисунке 4 точками представлено множество альтернатив в плоскости «стоимость-эффективность» для различных подсистем системы ИАэО.

На этом рисунке жирными линиями выделены области существования оптимальных по Парето альтернатив пFn, n = 1,3. Определение этих областей существенно снижает общее число подлежащих рассмотрению альтернатив, но не позволяет найти единственную, лучшую в каком-либо смысле альтернативу. В этом случае мы имеем задачу многокритериальной опти- мизации.

Известно [1, 2], что процедуры принятия решения при многих критериях условно можно разделить на априорные, апостериорные и адаптивные. Априорные процедуры не используют никакой дополнительной информации кроме известных целевых функций f i ( x ) е F . Для выбора наилучшей альтернативы в этом случае формируют глобальную функцию качества, в зависимости от ее вида различают принципы оптимальности. Так, функции вида

n

ф (x) = 2 h(x),                                                      (1)

i = 1

где глобальное качество представляет собой сумму локальных качеств, соответствует принцип равномерной оптимальности.

В ряде случаев применяют принцип справедливого компромисса, при этом глобальная функция качества имеет вид

Э 1

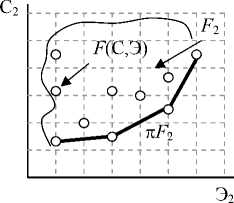
Рис. 4. Множество альтернатив построения подсистем ИАэО

n

ф (x) =П fi (x)•                                                     (2)

I = 1

Иногда используют глобальную функцию качества в соответствии с принципом гарантированного результата. Под наилучшей альтернативой здесь понимают максимально соответствующую совокупной цели на множестве альтернатив, при этом ее поиск осуществляется путем решения задачи вида f (x) ф (x) = max i

■ max ,

где f i - максимальное значение критерия f i ( x ).

Получил распространение для некоторых типов задач метод идеальной точки в пространстве критериев [3], предполагающий минимизацию метрики в пространстве векторных оценок между некоторой идеальной точкой, такой, что е = {е_ь...е _n }, где е _i = min f_i ( x ) и искомой альтернативой. ^{x e} X

Применение процедур априорного типа к исследуемой задаче вызывает определенные трудности. Так, использование глобальной функции качества (1) возможно, когда отдельные критерии имеют более или менее четко выраженную стоимостную окраску. Если критерии f_i ( x ) имеют различные единицы измерения, необходимо принимать меры к приведению функции (1) к безразмерному виду, но это сопряжено с необходимостью знания максимального и минимального значения f i ( x ) и при этом вклад «локального качества» в «глобальное качество» зависит от диапазона изменения значений критерия. Применение функций (2, 3) для решения поставленной задачи также затруднено ввиду неопределенности весов критериев в глобальном качестве системы, что может привести к несбалансированности характеристик отдельных подсистем системы инженерно-аэродромного обеспечения боевых действий авиации. Кроме того, в функции (3) необходимо знание максимального значения каждого критерия. Использование метода «идеальной точки в пространстве» требует введения некоторой метрики, причем при разных метриках наилучшими будут разные альтернативы. Поэтому выбор необходимой метрики задача не менее сложная, чем выбор наилучшей альтернативы.

Процедуры апостериорного типа предполагают формирование функции полезности, описывающей предпочтения лица, принимающего решение. Однако выбор вида этой функции связан с определенными трудностями как объективного, так и субъективного характера. Причем основное затруднение состоит в выборе языка предпочтений лица, принимающего решение. Эти предпочтения осуществляются за счет формирования функции полезности.

Для формирования этой функции необходимо проверить исходную гипотезу на независимость по полезности. Если ответы лица, принимающего решение, позволяют сделать вывод, что независимость действительно имеет место, то по принципу лотереи восстанавливаются все величины, необходимые для идентификации искомой функции полезности.

В [1] предложена апостериорная процедура Кини, основанная на понятии «независимости по полезности». Пусть существует векторная оценка f = (f1,f2,...,fm,...,fn). Представим ее в виде f = (v, v), где v=(f1, ..., fm) и v=(fm+1, ..., fn), причем veY veZ, F=YкZ. Необходимо найти неизвестную функцию полезности u(v,v). Ее поиск осуществляется через условные функции полезности. Условную функцию полезности на множестве Yопределяют путем фиксации v=v0, т.е. u(v0,v), а на множестве Z путем фиксации v=v0, т.е. v(v,v0). Считается, что Y не зависит по полезности от Z, если предпочтения лица, принимающего решение на Y при фиксированных v0eZ, не зависит от выбора v0. Это означает, что из u(V,v0) > u(v" ,v0) для v‘,v‘‘e Y и элемента v0eZ вытекает u(v‘,m) > u(v",ra) для любого veZ. В [105] функция полезности найдена в виде и (V , v) =

u ^{( v} ₀, ^{v) -} u ^{( v} ₀, ^v 0 ) 1 + ku ( V 0 , v o )

где u(v₀,v₀) = u(v,v(v)) = 0 - кривая равных полезностей; k - эмпирически оцениваемая константа.

Для формирования функции (4) необходимо проверить исходную гипотезу на независимость по полезности. Если ответы лица, принимающего решение, позволяют сделать вывод, что независимость действительно имеет место, то по принципу лотереи восстанавливаются все величины, необходимые для идентификации искомой функции полезности.

На практике такой подход наталкивается на определенные трудности, связанные с необходимостью сбора чрезвычайно большого количества информации, а также с тем, что лицо, принимающее решение, либо не может дать информацию, необходимую для реализации процедуры, либо дает ее с большими ошибками. Кроме того, возникают трудности в нахождении значения эмпирически оцениваемой константы k . Обилие информации, необходимой для реализации апостериорных процедур, затрудняет их применение на практике. Существенно уменьшить, а в ряде случаев и упростить требуемую от лица принимающего решение информацию при поиске наиболее предпочтительной альтернативы можно, не восстанавливая функцию полезности в явном виде. Процедуры, реализующие эту идею, называются адаптивными [4].

Среди адаптивных процедур хорошо зарекомендовал себя метод последовательных уступок [5], сущность которого состоит в следующем. Вначале все частные показатели f , i e l, n ранжируются по важности в порядке ее убывания: f 1 >  f 2 > ... f n , затем максимизируется первый по важности показатель f l ( х ) и определяется его максимальное значение ff^ax . После этого назначается величина его допустимого снижения (уступки) А ₁ и в области компромисса ищется наибольшее значение f /max второго по важности показателя f 2 ( х ) при условии, что значение первого показателя должно быть не менее чем f 1^max - А 1 . Затем назначается уступка А ₂ второго показателя и максимизируется третий показатель f ( х ) и т. д.

Последовательность действий при решении исходной задачи векторной оптимизации может быть представлена в виде f1max =supf1(x),(5)

x∈X f2max =     sup     f2(x) ,(6)

x∈X f1(x)≥ f1max-∆1

fnmax =       sup       fn(x) .(7)

x∈X fn-1(x)≥ fnmax-∆n-1

Решение последней задачи оптимизации (7) считается оптимальным решением задачи векторной оптимизации.

Величины уступок А 1 , А 2,... A n - 1 последовательно назначаются в результате изучения взаимосвязи частных показателей следующим образом. Вначале решается вопрос о назначении величины допустимого снижения ∆ ₁ первого показателя от его наибольшего значения f ₁ ^max . Для этого задают несколько величин уступок ∆ ¹1 , ∆ ²1 , ∆ ³1 … и путем решения (5) max ′ 1       max ′ 2 max ′ 3

определяют соответствующие максимальные значения f ₂    ( Δ 1 ) , f ₂     ( Δ 1 ), f ₂     ( Δ 1 )

второго показателя. Графически это показано на рис. 5. Из рисунка следует, что вначале даже небольшие величины уступок значений первого показателя позволяют получить существенный выигрыш по второму показателю, с дальнейшим увеличением уступки выигрыш растет медленнее. На основе анализа полученных данных назначается величина уступки ∆ ₁, а затем находят f 2 ( ∆ 1 ).

Далее рассматривают пару показателей f ₂, f ₃ и вновь назначают «пробные» величины уступок f ( ∆ ¹ ), f ( ∆ ² ), ... и согласно выражению (6) находят наибольшие значения третьего показателя f ₃ ( ∆ ¹ ₂), f ₃ ( ∆ ² ₂),... Полученные данные анализируют, назначают ∆ ₂, переходят к следующей паре показателей f 3 , f 4 и т. д. Наконец, в результате анализа взаимного влияния показателей f n –1 и f выбирается величина последней уступки Δ , и в соответствии с выражением (7) отыскивается оптимальное решение задачи.

f 1

f 1^max – Δ 1

f max max’ 1

f 1 – Δ 1 _{f 1}max’_{– Δ} 2_{1 f 1}max’_{– Δ} 3₁

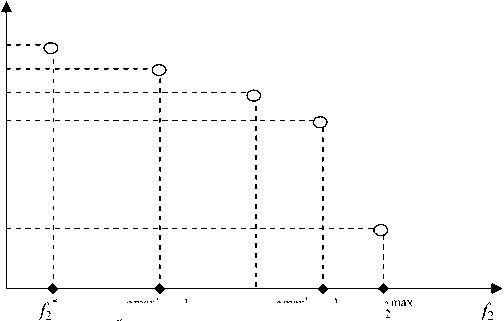
Рис. 5. Возможная зависимость значений показателей от величины уступок max 1 f2    (Δ 1)

f 2     ( Δ 1 )     f 2

Таким образом, применительно к рассматриваемой системе ИАэО данный метод можно использовать на этапе агрегирования ее подсистем в единую систему ИАэО. В качестве частных показателей необходимо рассматривать показатели эффективности подсистем системы ИАэО.

Adaptive Method of Consecutive Concessions at the Solution to the Problem of Vector Optimization of Characteristics of System of Engineering –