Адаптивный метод сжатия цветных изображений без потери информации

Изображения - это важнейшие источники информации о различных явлениях реального мира. Наряду с черно-белыми изображениями, в настоящее время во многих областях (например, в медицине, при создании баз данных о картинных галереях и т.п.) начинают широко использоваться многоградационные цветные изображения. Поскольку размеры описаний этих изображений их цветовыми составляющими R, G и В очень велики, возникает необходимость создать средства сжатия таких описаний; применение этих средств позволит снизить требования к объему внешних запоминающих устройств. При создании центров цифровой обработки изображений и баз данных, содержащих цветные изображения, особое значение приобретают методы сжатия изображений без потери информации. Существующие программы архивации данных, которые обеспечивают сжатие без потери информации, ориентированы в первую очередь на компактное представление текстовых файлов и весьма неэффективны даже в случае работы с много градационными черно-белыми изображениями [1],[2]. Единственная возможность использовать их для сжатия цветных изображений - это возможность сжимать каждую цветовую компоненту в отдельности.

Нами были разработаны методы и средства сокращенного описания многоградационных черно-белых изображений [1],[2]. Эти методы реализуют так называемое преобразование компонент с интерполяцией по отсчетам (ПКИО) -иерархическую процедуру интерполяционного кодирования. Поскольку указанная процедура учитывает известные статистические свойства реальных изображений [3], она оказывается весьма эффективным средством сжатия этих изображений без потери информации. Поэтому было решено создать новые варианты методов ПКИО, позволяющие сжимать цветные изображения реального мира и точно восстанавливать их. В данной работе описываются основные результаты разработки и реализации этих методов.

2.    СЖАТИЕ И ВОССТАНОВЛЕНИЕ МНОГОГРАДАЦИОННЫХ ЧЕРНО-БЕЛЫХ ИЗОБРАЖЕНИЙ

Прежде всего опишем вкратце, как выглядит метод ПКИО при работе с многоградационными черно-белыми изображениями (более подробное описание этого метода можно найти в [1],[2]). Блок-схема алгоритма сжатия черно-белого изображения методом ПКИО приведена на рис. 1. Алгоритм сжатия выглядит следующим образом:

• 1)    компандированное изображение Zq , полученное путем сжатия динамического диапазона исходного черно-белого изображения I_s и заданное отсчетами яркости

Работа частично финансировалась в рамках гранта "Разработка оптико-цифровых, параллельных, рекурсивных способов реализации методов и алгоритмов адаптивной обработки двумерных сигналов и изображений" Российского фонда фундаментальных исследований

Рис. 2. Алгоритм декодирования, использующий ПКИО

Рис. 1. Алгоритм кодирования, использующий ПКИО xij> ^^A^vi разбивается на компоненты 7^, ^=1,2,3, содержащие его прореженные отсчеты х^^у /j=0,l,2,... (например, четные отсчеты четных строк, отсчеты 0,4,8,... строк 0,4,8,... и тд.);

• 2)    с помощью билинейной интерполяции формируются промежуточные отсчеты х^ з^Ч^-ур Ч^Л^г” каждой из компонент 1^ (т.е. вычисляются полусуммы и четверти сумм их прореженных отсчетов). Важно отметить, что xW^ ^ ■ x^cj зд

• 3)    составляются разностные компоненты /л-/^ Ivh. и 72-7з; компонента Ik-V^k задается отсчетами У*"¹^-!; *-1у = x^/^My-xW^/^-iy, /J=0,l,2,... . Как показано в [1М2], при определении ^"-м целесообразно использовать вместо обычного вычитания вычитание по модулю 256, то есть пользоваться формулой у^*¹)^-!/jt-iy = (х^^-1/ ^-4 -x^^-i^-ij ⁺ 128)_moj256- Четверть отсчетов каждой из дифференциальных компонент (^"^^i^j) всегда имеет значение 0 (или 128). и эти отсчеты нет необходимости хранить.

Описанная процедура приводит к разложению изображения 7q на четыре компоненты: 7g-7j, Л"^ ^2"/з ^и ^3- К^ ^и обычное пирамидальное представление [4], представление изображения этими компонентами можно в первом приближении считать разбиением на полосы различных пространственных частот. Так, компонента /3 описывает низкочастотные свойства изображения, компонента I2-I3 - полосу несколько более высоких пространственных частот и т.д. Представление изображения компонентами ПКИО, однако, выгодно отличается от его пирамидального представления тем, что компоненты ПКИО имеют тот же объем, что и кодируемое изображение (размеры пирамидального представления, как известно, на 1/3 превышают объем изображения).

Благодаря хорошо известным свойствам изображений реального мира (в первую очередь - высокой корреляции отсчетов в пределах сравнительно протяженных гладких областей) процедура формирования разностных компонент ПКИО (приводящая к декорреляции этих отсчетов) порождает компоненты, которые имеют гораздо меньшую суммарную энтропию, чем исходное изображение. Поэтому результаты ПКИО легко сжать, применяя обычные средства статистического кодирования (например, код Хафмана [5]). Отсчеты базовой компоненты I3 занимают всего 1/64 общего объема описания, а их энтропия велика. Поэтому указанные отсчеты целесообразно хранить непосредственно, не используя статистического кодирования.

Блок-схема алгоритма декодирования изображения, сжатого с помощью ПКИО, показана на рис.2. Первый этап декодирования сводится к расшифровке кодовых слов кода Хафмана и точному восстановлению компонент Z3, Z2-Z3, Л~^2 и Л)"Л- Дальнейшее декодирование выполняется следующим образом:

• 1)    посредством билинейной интерполяции (см. шаг 2 описанного выше алгоритма кодирования) восстанавливаются промежуточные отсчеты х^³) компоненты /3 (напомним, что *®8i,8j ⁵ *8;,8у);

• 2)    к значениям отсчетов, найденным по окончании шага 1, добавляются значения отсчетов ^\^ разностной компоненты Z2-Z3. ® результате точно восстанавливаются отсчеты Х4/4У = (/2)4; 4j ⁺^⁽³^4/ 4/ ^-128)_mo<i256> ^ 7=0,1,2,... компоненты Z2;

• з)    - 4) шаги 1 и 2 повторяются для отсчетов компонент /2 ^и Л~^2- При этом восстанавливается компонента 1у;

• 5)    - 6) еще одно повторение интерполяции и суммирования, на сей раз для компонент 1^ и Zq-Zj, приводит к точному восстановлению компандированного изображения Zq;

• 7)    для восстановления исходного изображения I_s отсчеты изображения Zq подвергаются табличному преобразованию, восстанавливающему исходный диапазон яркости.

3.    СЖАТИЕ И ВОССТАНОВЛЕНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ

В отличие от параллельной процедуры кодирования, алгоритм декодирования является принципиально последовательным, поскольку компоненту Z2, компоненту Z} и изображение Zq приходится восстанавливать поочередно.

Успешное применение ПКИО для сжатия черно-белых изображений [1],[2] вдохновило нас на использование аналогичной процедуры для сокращенного описания цветных изображений реального мира без потери информации. Проще всего независимо сжимать методом ПКИО каждую из цветовых составляющих R, G и В цветного изображения (рис. 3). Составляющие большинства реальных цветных изображений, как правило, сильно коррелированы; желательно использовать это обстоятельство для увеличения степени их сжатия. Способы декорреляции цветовых составляющих в случае кодирования с потерями информации хорошо известны: необходимо вычислять взвешенные суммы этих составляющих Л^оцЯ+р^бЧ^Д У=а2^4-32^72^ ^и Z^a^R+^G-H^B. Нетрудно найти оптимальный набор коэффициентов {а^, р£, у^> применение которого обеспечивает минимальную среднеквадратичную погрешность восстановления цветовых компонент (см., например, [3]). К сожалению, при необходимости восстанавливать изображения без потери информации использовать дробные коэффициенты почти невозможно, поскольку повторное квантование взвешенных сумм ведет к потере информации. Попытки работы с целыми коэффициентами вместо дробных посредством увеличения длины кодовых слов приводят к значительному расширению описания и к увеличению энтропии данных; в результате

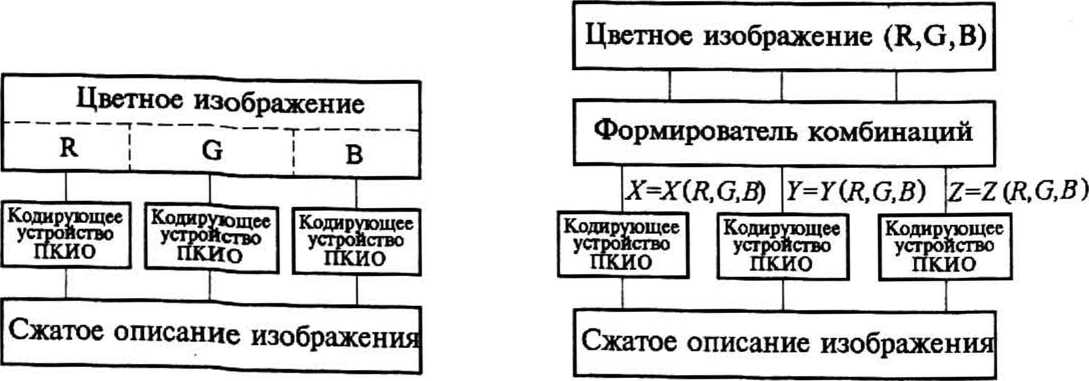
Рис. 3. Простейшая возможность кодирования цветных изображений

Рис. 4. Улучшенный метод кодирования цветных изображений эффективность кодирования резко падает. Единственной реальной возможностью является применение усеченных взвешенных сумм (УВС) пар цветовых составляющих (можно, например, использовать УВС Я+^б и В+р26). Один из весовых коэффициентов в каждой сумме должен равняться единице. Если в дополнение к УВС располагать информацией о составляющей с дробным весом (в приведенном примере -б), то можно точно восстановить составляющие с единичными весами (7? и В). Полный перечень возможных УВС будет приведен ниже. Если вычислять УВС по модулю 256 (теоретические предпосылки целесообразности этого можно найти в [6]), то объем описания цветного изображения с помощью цветовых составляющих и их УВС (Л, У и 2) окажется равным суммарному объему цветовых составляющих R, би В. Каждую из составляющих X, Y и Z можно сжать с применением какого-либо метода кодирования, например, описанной выше процедуры ПКИО (рис. 4).

Если использовать в качестве средства сжатия метод ПКИО, то можно предложить и другой вариант кодирования цветных изображений. В самом деле, можно находить взвешенные суммы и после реализации ПКИО, вычисляя их для триад разностных компонент, полученных на каждом из трех иерархических уровней этого преобразования. Будем называть этот вариант "методом ПКИО с комбинированием компонент". Он имеет ряд преимуществ по сравнению с непосредственным комбинированием цветовых составляющих изображений. Во-первых, результаты моделирования указывают на его более высокую эффективность; повышение эффективности объясняется лучшей адаптацией комбинаций компонент ПКИО различных уровней к свойствам составляющих кодируемого цветного изображения в различных диапазонах пространственных частот. Кроме того, при применении метода ПКИО с комбинированием компонент отпадает необходимость согласовывать динамические диапазоны этих компонент, поскольку функции распределения разностных компонент ПКИО всегда имеют сходные быстро спадающие распределения с максимумом в нуле (или в точке 128 при вычислениях по модулю 256). В связи с наличием указанных преимуществ именно метод ПКИО с комбинированием компонент будет являться основным объектом дальнейших исследований.

3.1.    Метод ПКИО с комбинированием компонент

Блок-схема алгоритма, реализующего метод ПКИО с комбинированием компонент, показана на рис. 5. Этот алгоритм имеет следующий вид:

• 1)    сжимается динамический диапазон цветовых составляющих R, G и В кодируемого цветного изображения. Такая предварительная процедура необходима для предотвращения возможного увеличения числа значений отсчетов разностных компонент после ПКИО (как показано в [1],[2], оно может привести к резкому снижению эффективности кодирования в случае, если число значений отсчетов реальных цветовых составляющих значительно меньше максимально возможного числа этих значений (256);

• 2)    каждая из составляющих, полученных после выполнения первого шага (Rq, бу и Bq) подвергается ПКИО. В результате кодируемое изображение представляется тремя базовыми компонентами - R3, G3 и В3 и тремя триадами разностных компонент -^В23⁼В2~Кз> А 633—62-63, Д^З⁼^"^зЬ (А^12⁼-^1"^2’ ^^12⁼^1~^2’ ^ВузуВу-Вз) и {ДЛ_О1=2?0-Л_Ь дG₀₁=Gq-Gy &Bqx=Bq-Bx}, которые отвечают различным диапазонам пространственных частот;

• 3)    триады разностных компонент комбинируются с помощью трех формирователей комбинаций. Для этого вычисляются все возможные УВС этих компонент и для каждого из трех иерархических уровней находится наилучшая комбинация компонент и УВС (эта процедура будет подобно описана ниже). В результате формируются три триады новых компонент - кХзз^ВззДСззДВ^з), Y^^R^AG^AB^), ХззДВззДСззДВзз)), \.ХхзАВх1ДОх2ДВх2^ Yxi^RiiAGxiABxi), Zx2№n^^Gn^^BYl)} и {^(AltObAGbiABbi), Уо1(^лЛОЬ^АСЬь^д5О1)> ^о^А^о^Дбу^А^ох)};

• 4)    для компактного представления компонент Хр Y^ и Zj, как и при работе с чернобелыми изображениями, используется код Хафмана. Максимальное сжатие при этом Достигается в случае, когда для кодирования каждой из девяти компонент используется своя кодовая книга. Поскольку объем базовых компонент R3, G3 и В3 очень мал

3.2.    Формирователи комбинаций и блоки восстановления компонент

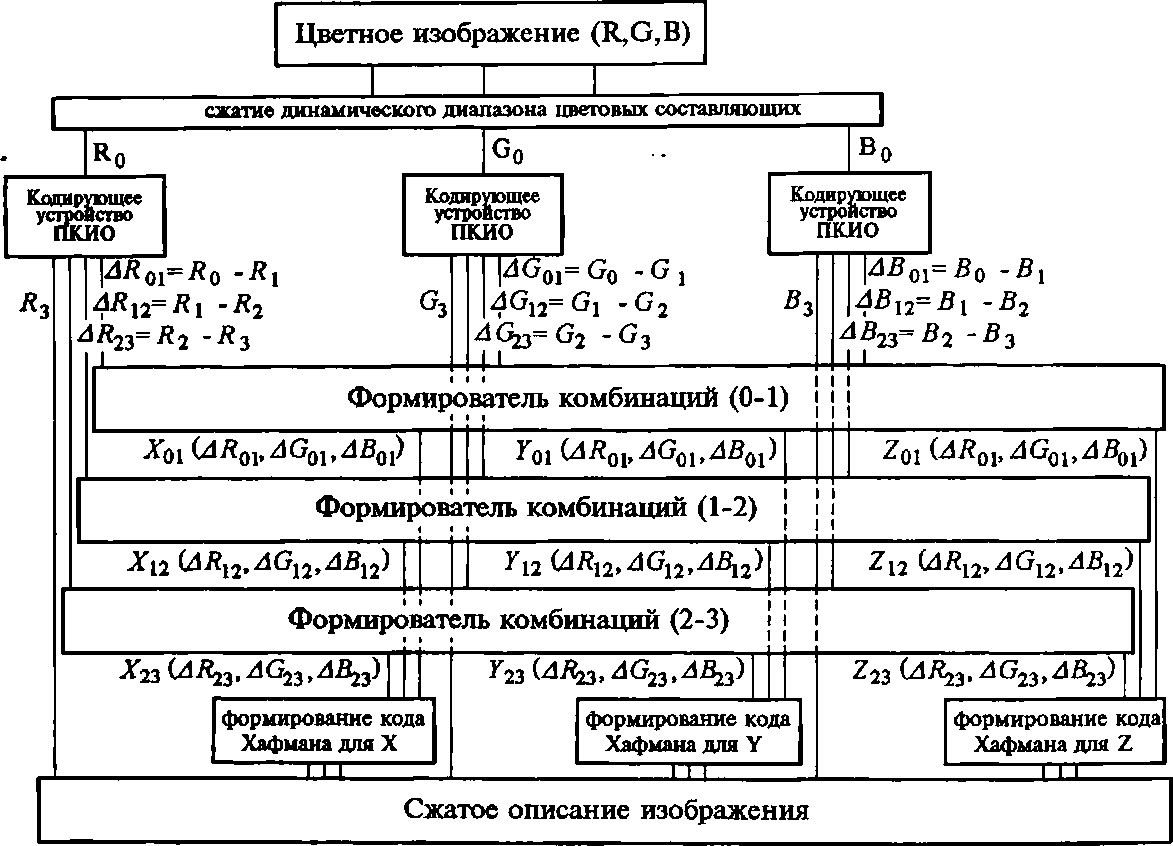
Рис. 5. Алгоритм кодирования, реализующий метод ПКИ О с комбинированием компонент

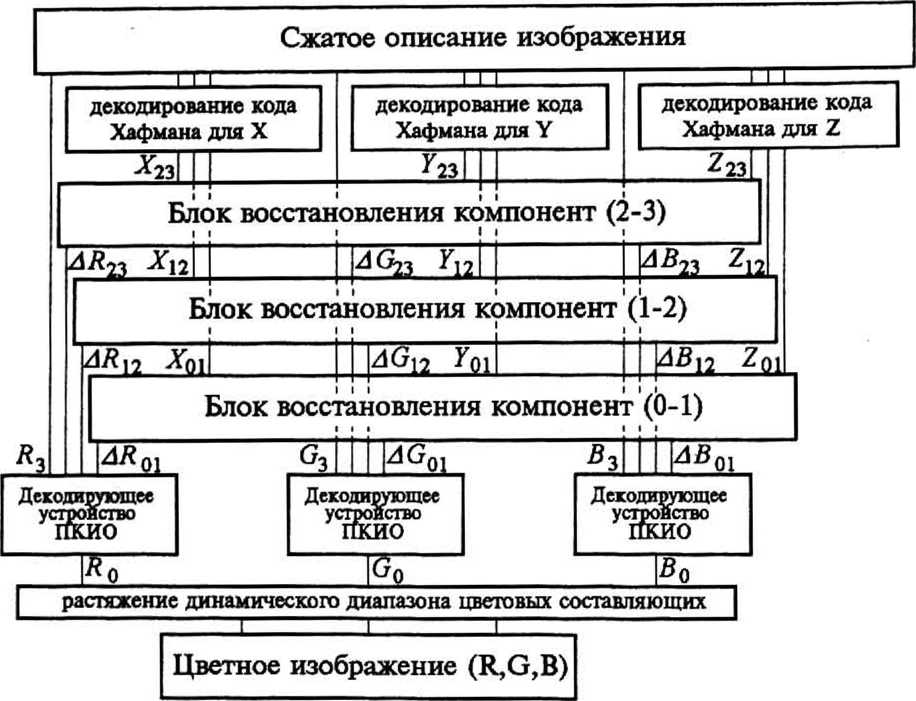
Рис. 6. Алгоритм декодирования изображения, сжатого методом ПКИО с комбинированием компонент

(1/64 общего объема описания), а их энтропии обычно велики, лучше всего непосредственно хранить отсчеты этих компонент, не применяя для них статистического кодирования.

Процедура восстановления цветного изображения, сжатого методом ПКИ О с комбинированием компонент (рис. 6) фактически является инверсией процедуры сжатия, показанной на рис. 5. Ее первым шагом является декодирование кодовых слов Хафмана и восстановление компонент Х23, Д2’ ^ОЪ ^23> ^12» ^ОЬ ^23>^z12 ^и ^01- Затем в трех блоках восстановления находятся разностные компоненты AS23, ^12» ^д^0Ь ^д^23>^д<^12> Дбу1, AS23, AS]^ ^{и Д}А)1 ^для ^^ цветовых составляющих. Применение обратного ПКИО (см. рис. 2) к каждой из трех триад разностных компонент (и соответствующим базовым компонентам -S3, G3 или S3) приводит к точному восстановлению компандированных цветовых составляющих Rq, Gq и Bq. После этого достаточно подвергнуть их трем табличным преобразованиям, восстанавливающим динамические диапазоны, чтобы восстановить исходные цветовые составляющие R, Gm В.

Совершенно очевидно, что эффективность показанного на рис. 5 алгоритма сжатия всецело зависит от способа комбинирования компонент в формирователях комбинаций. Как уже отмечалось выше, единственной доступной возможностью является вычисление для этих компонент УВС вида U+сУ, для того, чтобы определить каждую такую УВС, необходимо найти один коэффициент.

Список возможных комбинаций X(AR, ^G, SB), Y[SR, А (г, AS) и Z^SR, SG, SB) трех компонент AS, А С и AS и их УВС приведен в табл. 1 (напомним, что УВС естественно вычислять по модулю 256). Легко видеть, что приведенные в таблице шестнадцать комбинаций исчерпывают их перечень (с точностью до перестановок); комбинации, не включенные в таблицу (например, {Л^АЛ+рАС, ^ДСТ+уДД Z=AS+aAS}) порождают системы зависимых уравнений, из которых нельзя найти AS, А (7 и AS. Для обеспечения максимальной эффективности нашего алгоритма сжатия, в котором используется статистическое кодирование, необходимо выбрать на каждом из трех иерархических уровней I (01, 12 или 23) такую комбинацию тц и такие коэффициенты а/, р/ или у/, чтобы получить минимально возможную суммарную энтропию Нп^Нхл+Нущ+Нхл. . К сожалению, нет возможности найти энтропию взвешенной суммы, исходя из статистики слагаемых. Поэтому невозможно и найти оптимальные коэффициенты. В нашем распоряжении имеется лишь субоптимальная процедура, гарантирующая получение УВС с минимальной дисперсией (что совсем не всегда приводит к наилучшему статистическому сжатию этих УВС). Субоптимальное значение весового коэффициента с в УВС W=U-VcV определяется формулой

^С— ~Хиу/^ >  (1) где Хцу =Е(£Т) - Е({7)Е(Ю - ковариация компонент U и У, Dy = Е^) - (Е(Р))² -дисперсия компоненты У, Е(*) - математическое ожидание случайной величины ♦. При субоптимальном выборе с достигается минимальное значение дисперсии D^y УВС W:

^W ⁼ ^;(1 ^—^)> * (2)

где Dy = ^lP-) - (E(t/))² - дисперсия компоненты U, к = Хцу / ^DuDy - коэффициент корреляции компонент U и У.

Применение описанной субоптимальной процедуры приводит к следующему алгоритму адаптации формирователей комбинаций каждого из трех иерархических Уровней / (01, 12 и 23) к статистическим свойствам разностных компонент кодируемого Цветного изображения (рис. 7а):

Выбор комбинации с наименьшей суммарной дисперсией ⁿ afopt l^opt ^Opt

Выбор комбинации с наименьшей суммарной энтропией

|”/opt б

a

Рис. 7. Адаптация формирователей комбинаций к содержимому цветного изображения: а - при применении УВС с оптимальными весами;б - при использовании попарных разностей

• 3)    выбирается комбинация л/_ор1, которой отвечает наименьшее значение D_n..

В результате адаптации для каждого иерархического уровня определяется номер оптимальной комбинации и величины одного или двух отвечающих этой комбинации коэффициентов, минимизирующих суммарную дисперсию.

Поскольку реализация описанного метода адаптации требует большого объема вычислений, а получаемые оценки статистических характеристик невозможно использовать при последующем кодировании компонент, интересно рассмотреть и более простую процедуру адаптации. Она предполагает все коэффициенты в УВС априори равными -1, то есть в ее рамках объектами статистического кодирования являются комбинации разностных компонент и их попарных разностей по модулю 256 (см. табл. 2). При этом алгоритм адаптации для иерархического уровня i выглядит следующим образом (рис. 76):

• 1)    строятся шесть гистограмм распределений для разностных компонент kR^ ^Gj и ЬВ;, а также для их попарных разностей (по модулю 256):ДДК;), P^G^, Д^В^, ДЫк}-^), ДД^-дЯ^иЛАЯ^);

• 2)    по этим гистограммам находятся 6 значений энтропии Н = -^/(к) • log₂ /(^); к

• 3)    для каждой из 16 перечисленных в левой части табл. 2 комбинаций л/ определяется суммарная энтропия Н_п^-Н^_п.+Ну_п ^Н/п.;

• 4)    выбирается комбинация л; , которой отвечает наименьшее значение Н_п.. Описанный способ адаптации минимизирует суммарную длину кода Хафмана для выбранной триады компонент Х_п-, Y_n. и Z_np это означает, что он действительно является оптимальным. Гистограммы, построенные на этапе адаптации, могут быть использованы при построении кодовых книг кода Хафмана.

3.3.    Дополнительная информация

Проведенное моделирование показало, что работа с попарными разностями компонент при сжатии цветных изображений реального мира методом ПКИО ухудшает степень сжатия менее, чем на 1% по сравнению с применением УВС. Более того, оптимальные значения коэффициентов УВС в большинстве практических случаев оказываются близкими к -1. При этом алгоритм адапт аци и рис. 76, работающий с попарными разностями, иногда оказывается даже более эффективным, чем алгоритм рис.7а, использующий УВС, поскольку процедура поиска коэффициентов является лишь субоптималъной. Таким образом, на практике целесообразно вычислять в формирователях комбинаций попарные разности компонент и использовать оптимальную процедуру адаптации рис. 76.

Структура блоков, обеспечивающих восстановление компонент ДЯ/, AG/ и ^B^ в декодирующем устройстве по номеру выбранной комбинации л^ и компонентам Х_п^ Y^

Таблица 2. Возможные комбинации компонент и их попарных разностей по модулю 256 (левая часть); аналитические решения, позволяющие восстановить AR, AG и АВ (правая часть)

и X^R, aG, AS) y(&R, a^ aS) Z(AR, AG, AB) двау^ Д^ХУ.Х) дВ(ХУ^ 1 AR aG AB X z 2 AR-AG aG AB X+Y У z 3 AR-ДВ AG AB X+Z Y 4 aR aG-aB AB X Y+X z 5 AR AG-AB AB X Y+Z z 6 aR AG AB-AR X У Z+X 7 AR aG AB-AG X Y Z+Y 8 AR ag-aR AB-AR X У+Х Z+X 0 aR AG-Ak AB-AG X Y+X Z+Y+X 10 aB AG-AB AB-AR X Y+Z+X z+x И ar-ag AG AB-AG X+Y Y Z+Y 12 AR-AG AG AB-AR У+У Y Z+X+Y 13 aR-aB AG AB-AG X+Z+Y Y Z+Y 14 aR-aB " AG-ДВ aB X+Z Y+Z Z 15 AR-AB AG-AR AB X+Z Y+X+Z z 16 AR-AG AG-AB AB X+Y+Z Y+Z z и Zn^ совершенно очевидна. В этих блоках должно определяться решение системы уравнений, отвечающей п;. Нетрудно найти такие решения аналитически для всех возможных комбинаций. При работе с попарными разностями процедура восстановления сводится к суммированию (по модулю 256) компонент Хп., Yn. и Zn- (см. правую часть табл. 2).

При оценке реальной эффективности предложенного метода сжатия цветных изображений не следует забывать о необходимости хранить некоторое количество дополнительной информации. Во-первых, компоненты X, Y и Z на каждом иерархическом уровне имеют различные статистические свойства. Поэтому степень сжатия оказывается максимальной в случае, когда для кодирования компонент %q], ^2, ^23’ %, ^12» ^3» ^ОЬ ^12 ^и ^23 используется 9 различных кодовых книг Хафмана. Для декодирования кодов Хафмана необходимо иметь информацию об этих кодовых книгах. Каждая из них содержит 256 кодовых слов, длина которых переменна и может составлять до 4 байтов. При непосредственном хранении объем книги доходит до 1184 байтов [1],[2]. Поскольку вид кодовой книги Хафмана однозначно определяется статистикой кодируемых данных, можно вместо нее хранить гистограмму их распределения. В нашем случае эти гистограммы имеют выраженный максимум, и их можно компактно описать с помощью простого кода, похожего на код Хафмана [1],[2]. При этом для хранения всех девяти гистограмм требуется лишь около 900 байтов дополнительной информации.

Помимо информации о гистограммах, для правильного декодирования необходимо иметь информацию о трех таблицах, использованных для сжатия динамических диапазонов цветовых составляющих на первом этапе процедуры кодирования. Метод компактного описания этих таблиц описан в [1],[2]; при его применении объем их описания составляет всего 100-180 байтов.

Для работы блоков восстановления компонент необходимо знать номера наилучших комбинаций на каждом из иерархических уровней. Эти номера можно непосредственно запомнить, используя 1,5 байта памяти.

Таким образом, общий объем дополнительной информации составляет около 1000 байтов.

4.    ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ

Описанный выше метод сжатия цветных изображений был реализован в виде двух завершенных программ (CPRESS и CUNPRESS) для IBM-совместимых персональных ЭВМ. С помощью этих программ можно сжимать (и восстанавливать без потери информации) цветные изображения любых размеров, заданные в виде трех файлов с цветовыми составляющими R, G и В в байтовом формате. Большая часть текста этих программ написана на языке "Си"; для повышения их быстродействия в некоторых местах использовался также язык "Ассемблер".

Для оценки возможностей предложенного метода использовались высококачественные цветные изображения (изображения картин с высокой насыщенностью и детальностью, качественные цветные фотографии и спектрозональное спутниковое изображение). Их энтропия была достаточно высокой (до 21,9 бит). В ходе экспериментов определялся коэффициент сжатия S - отношение длины файла, получаемого в результате кодирования, к суммарной длине трех файлов, изначально чапающих цветное изображение (чем меньше S, тем больше степень сжатия). Для сравнения мы сжимали каждую из трех составляющих R, G и В цветного изображения с помощью программы PRESS (которая реализует кодирование черно-белых изображений методом ПКИО). Это отвечало простейшей схеме кодирования, приведенной на рис. 3. Возможности программы PRESS были изучены в [1],[2]; ее применение обеспечивало сжатие черно-белых изображений в 2-3 раза и являлось на 10-30% более эффективным, чем использование обычных средств архивации (программ PKZIP, LHA и ARJ).

Таблица 3. Экспериментальные результаты

Изображение	Объем исходного описания, байт	Размеры изображения	Энтропия, бит	Коэффициент сжатия S, %		Xpress - •^CPRESS’0/0
				3xPRESS	CPRESS
"Фрукты"	786432	512x512	21,9	61	54	7
"Барабанщики"	691200	512x450	21,3	59	57	2
"Христос"	2674305	1005 х887	20,6	60	57	3
"Святой"	1874763	653 х 957	21,2	73	68	5
"Одесса"	6140928	1999 х 1024	15,6	40	39	1

Результаты измерений коэффициентов сжатия приведены в табл. 3. Они указывают на то, что применение программы CPRESS для сжатия цветных изображений до 7% более эффективно, чем трехкратное применение протраммы PRESS для сжатия их цветовых составляющих. Получаемый выигрыш более высок для изображений с сильно коррелированными составляющими (например, для изображения "Фрукты"). Корреляция составляющих в спектрозональном изображении "Одесса" значительно ниже; поэтому и выигрыш для него оказывается незначительным. Абсолютные значения коэффициентов сжатия при применении протраммы CPRESS оказываются достаточно малыми; объем сжатого изображения может доходить до 1/3 объема его исходного описания.

Высокая эффективность программ CPRESS и CUNPRESS означает наличие широких возможностей их практического использования в системах обработки изображений и в базах видеоданных различных типов. Эти протраммы могут быть предоставлены в распоряжение всех потенциальных потребителей.