Адаптивный шифр с пространственно-временным распылением информации

Постановка задачи

Созданию скрытых каналов связи, основанных на внедрении латентной информации в криптограммы, посвящено ограниченное число публикаций. В этом направлении можно отметить работы Г. Симмонсона, разработавшего методы формирования скрытого канала связи на основе схемы идентификации (цифровой подписи и проверки подлинности) Онга-Шнорра-Шамира [2] и схем подписи [6]: Эль-Гамаля [3], ESIGN [4] и DSA [5]. Из отечественных публикаций выделим работу, посвященную возможности установления скрытого канала связи в системе цифровой подписи ГОСТ Р 34.10-2001 [8].

Основная идея этих работ сводится к тому, чтобы криптограмму сделать переносчиком (контейнером) для передачи дополнительной скрытой информации. В данной статье для решения подобной задачи предлагается способ пространственно-временного распыления зашифрованной информации.

Пространственно-временное распыление информации

Основная идея данной работы заключается в дроблении криптограммы на несколько блоков (не обязательно равных) и передаче их по нескольким каналам связи (распыление в пространстве) и в различные (неопределенные для противника) моменты времени (распыление во времени). Такая процедура создает перед криптоаналитиками дополнительный барьер защиты. Очевидно, что, помимо традиционных проблем с атакой на шифр, возникают проблемы с перехватом всех сообщений и выстраиванием их в нужном порядке.

Под каналами связи будем понимать не только традиционные каналы связи (радио, радиорелейные, спутниковые, кабельные, почтовые), но и передачу информации с помощью мультимедийных контейнеров (графики, текста, звука, видео). При этом передачу можно осуществлять с помощью электронной почты, мессенджеров, чатов, SMS, MMS, Web-страниц, микроблогов, файлообменных сетей.

Предлагается передачу блоков криптограммы осуществлять не последовательно и не непрерывно, а в порядке, который определяется генератором псевдослучайных чисел (ГПСЧ). При этом ГПСЧ определяет, какой из множества блоков криптограммы передается, по какому каналу и в какой момент времени. Таким образом, сформированная псевдослучайная последовательность становится элементом секретного ключа.

Помимо информационных блоков, по каналам связи можно передавать маскирующие (дезинформирующие) блоки.

Каждый информационный блок на передаче получает порядковый номер, с помощью которого сообщение на приеме восстанавливается в исходной последовательности, вне зависимости от порядка и времени поступления блоков. В данном шифре стеганограм-мой будет являться порядковый номер блока криптограммы.

Естественно, что номера блоков должны оставаться скрытыми от противника. Скрытая нумерация блоков может осуществляться криптографическими или стеганографическими способами. В первом случае блок криптограммы должен содержать порядковый номер этого бло- ка. Номер блока должен быть зашифрован тем же ключом, что и вся криптограмма.

Для реализации шифра с пространственновременным распылением информации необходимо выполнить две операции: разбить криптограмму на блоки и скрытно пронумеровать эти блоки.

Стеганографическое внедрение информации

За основу разрабатываемого шифра был взят адаптивный многоалфавитный шифр с интегральным преобразованием [7], где во время генерации пределов интегрирования происходит выравнивание высоты столбцов гистограммы, которая описывает распределение чисел в криптограмме. Первый (например, нижний) предел интегрирования выбирается случайно среди чисел из интервалов (столбцов) гистограммы с наименьшим заполнением (наименьшей высоты). Значения интеграла выбираются случайно из

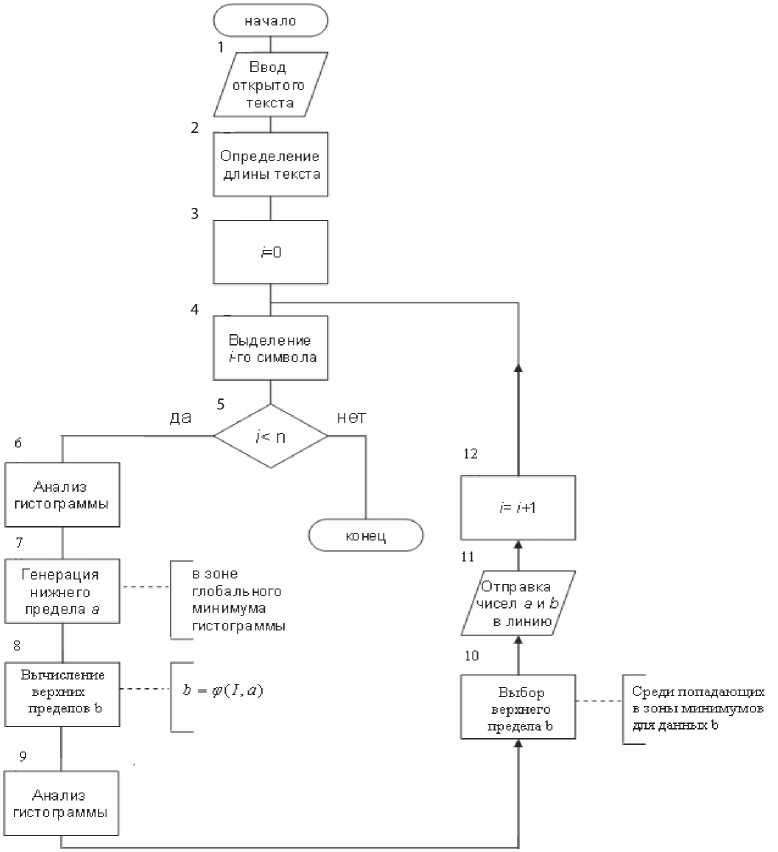
Рис. 2. Блок-схема адаптивного многоалфавитного шифра

всех допустимых диапазонов таблицы многоалфавитной замены (ТМЗ) для шифруемого символа, и производятся предварительные расчеты второго (например, верхнего) предела интегрирования. Среди полученных вторых пределов интегрирования выбираются те числа, которые попадают в локальные минимумы гистограммы. Если имеется несколько допустимых интервалов (столбцов), то выбирают один из них по случайному закону. Верхний и нижний пределы интегрирования являются элементами криптограммы, и их передают на приемную сторону.

Блок-схема рассмотренного алгоритма показана на рис. 2. Номер каждого блока криптограммы представляют в двоичной системе счи- сления. При сокрытии считывается внедряемый бит двоичного числа, и если он равен 1, то при шифровании выбирается столбец, ближайший к началу гистограммы (если допустимо, то используется крайний левый столбец). Если внедряемый бит равен 0, то выбирается столбец гистограммы (точнее – интервал) с максимальным удалением от начала числовой оси (крайний правый столбец).

Если отсутствует выбор среди столбцов (то есть остается единственный допустимый интервал гистограммы), то внедрение стеганограммы переносится на следующие шаги алгоритма (см. рис. 3). На приемной стороне после расшифровывания переданного сообщения по полученным

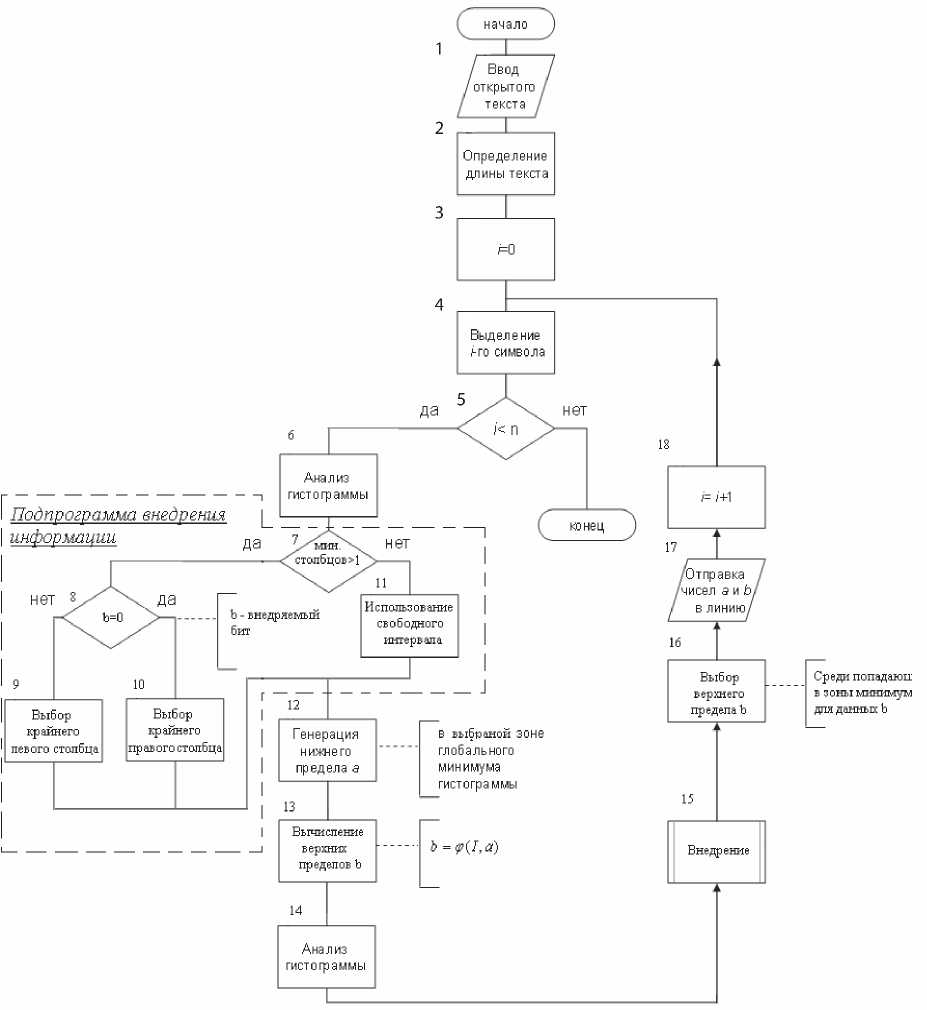
Рис. 3. Блок-схема алгоритма внедрения информации

нижним и верхним пределам интегрирования и вычисленным значениям интеграла производится поэтапное восстановление (реконструкция) гистограммы. При этом на приеме необходимо восстановить последовательность заполнения гистограммы, реализованную на передающей стороне.

Рассмотрим пример, в котором таблица многоалфавитной замены составлена так, что при заданной подынтегральной функции, например, x ², выбор предела интегрирования может осуществляться из всех интервалов гистограммы. Допустим, что число интервалов (столбцов гистограммы) пять. Пусть очередному блоку криптограммы требуется присвоить порядковый десятичный номер 44 (в двоичной системе счисления 101100).

В первоначальном состоянии гистограммы (в момент начала шифрования) все интервалы гистограммы пустые. Так как первый бит (старший бит числа) скрываемой стеганограммы равен 1, то выбирается предел интегрирования из интервала первого столбца гистограммы (крайний левый столбец на рис. 4a).

Далее производится предварительный расчет второго предела интегрирования для всех возможных значений интеграла для данной шифруемой буквы. В данном примере ТМЗ составлена так, что предел интегрирования может попасть в любой столбец. На данном этапе идет выбор между интервалами (столбцами) 2…5. Так как второй бит скрываемой стеганограммы равен 0, то выбирается число (предел интегрирования) из пятого столбца (крайний правый столбец на рис. 4б).

Рассмотрим процесс шифрования второй буквы открытого текста. Интервал выбирается среди столбцов с номерами 2…4. Так как нужно скрыть бит со значением 1 (третий бит), то выбирается столбец 2 (крайний левый среди минимально заполненных на рис. 4в). Для значения второго предела интегрирования выбирается область определения среди столбцов 3 и 4. При сокрытии четвертого бита стеганограммы, который равен 1, выбирается третий диапазон (крайний левый среди минимально заполненных, на рис. 4г). Следующий этап – выбор интервала для первого предела интегрирования третьей буквы. В этой ситуации выбора нет, так как есть только один допустимый интервал – четвертый, откуда и выбирается очередной предел интегрирования. В подобных случаях (когда нет выбора между двумя допустимыми столбцами) скрыть очередной бит стегано-граммы невозможно. В такой ситуации сокрытия информации не происходит, а идет штатное формирование криптограммы (см. рис. 4д).

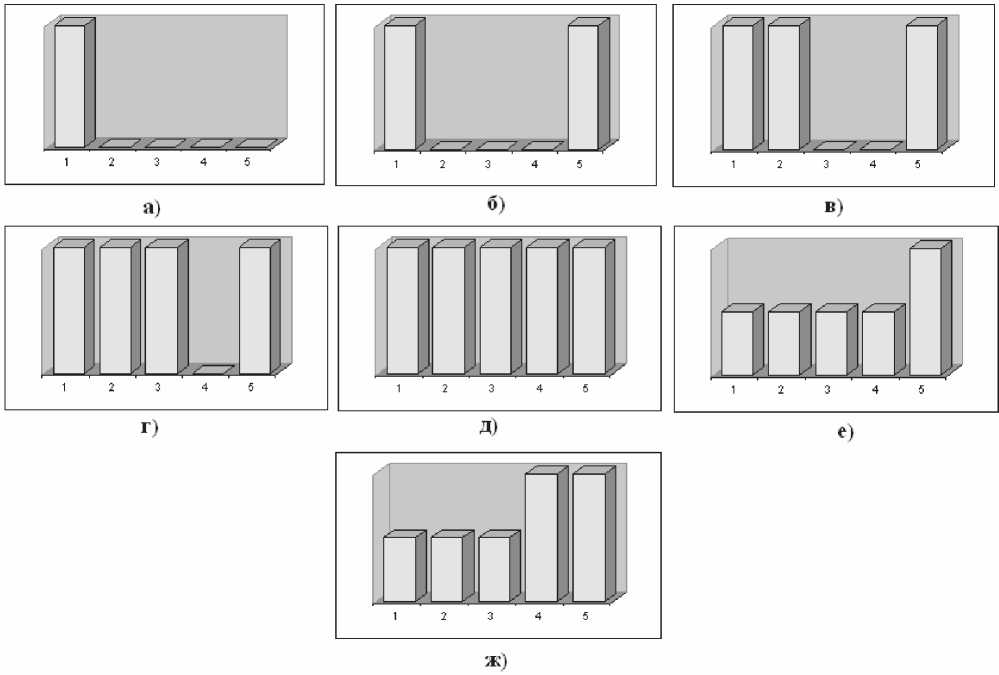
Рис. 4. Этапы построения гистограммы

Затем выбирается второй предел интегрирования для третьей буквы. Сейчас интервалов с минимальным заполнением пять – 1, 2, 3, 4 и 5. Теперь требуется скрыть пятый бит стеганограммы, равный 0. Выбирается крайний правый столбец – пятый (см. рис. 4е). Далее выбирается первый предел интегрирования для четвертой буквы из интервалов с номерами 1, 2, 3 и 4. Так как требуется скрыть бит, равный 0, то выбирается четвертый интервал (крайний правый допустимый на рис. 4ж).

Разбиение криптограммы на отдельные блоки

Разбиение криптограммы на блоки происходит в тех местах алгоритма (в те моменты времени), где при шифровании все столбцы гистограммы имеют одинаковую высоту.

Таким образом, каждый блок криптограммы на приеме можно расшифровывать отдельно, задав все начальные значения гистограммы нулевыми. Это приведет к верному расшифровыванию каждого блока криптограммы и правильному извлечению скрытого номера блока.

Проверка рассмотренного способа шифрования была осуществлена путем разработки программы «Samara cherry fox».

Выводы

Разработанный шифр создает перед криптоаналитиками дополнительный барьер, состоящий в необходимости перехвата всех блоков криптограммы, передаваемых по разным каналам связи. Проведенная экспериментальная проверка подтверждает эффективность рассмотренной идеи.