Адаптивный спектрально-инерционный слой на основе обучаемой маски фурье-преобразования для фильтрации выходных данных в задачах прогнозирования физиологических временных рядов

Современные системы мониторинга при подготовке спасателей и промышленного персонала, работающих в экстремальных условиях, прогнозируют динамику ключевых физиологических показателей, таких как лёгочная вентиляция, объём потреблённого кислорода и др., для оценки готовности человека к выполнению предстоящей нагрузки, контроля за допустимым уровнем утомления, своевременного предупреждения о возможном риске гипоксии или перегрузки, а также для расчёта оставшегося ресурса изолирующего дыхательного аппарата [1–3].

Для решения задач прогнозирования физиологических временных рядов последнее время всё шире применяются рекуррентные нейронные сети (RNN), особенно модели долгой краткосрочной памяти LSTM (Long Short-Term Memory) и GRU, способные учитывать длительные зависимости и нелинейную динамику физиологических процессов. Однако, несмотря на высокую точность предсказания, выходные сигналы таких моделей могут содержать нежелательные колебания, возникающие при резких изменениях условий или в случае ограниченного объёма тренировочных данных. Эти флуктуации зачастую не соответствуют реальной физиологической динамике и затрудняют интерпретацию результатов, особенно в задачах, требующих плавного, интерпретируемого и устойчивого поведения модели на выходе.

В этих условиях традиционно используют классические цифровые фильтры нижних частот (Баттерворта, Чебышева, Бесселя), медианные фильтры и сглаживание на основе скользящего среднего. Эти методы эффективны на этапе предварительной обработки данных, поступающих от сенсоров, и позволяют получить устойчивые входные данные

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

для обучения модели. Именно они широко используются при предварительной обработке исходных данных. Однако предварительная фильтрация исходных данных не устраняет нестабильность выходных предсказаний.

Применение классических цифровых фильтров на выходе модели [4], уже после этапа прогнозирования, оказывается методологически и практически несостоятельным. Во-первых, такие фильтры являются фиксированными – параметры фильтра (порядок, частота среза, фаза) не адаптируются к особенностям выходного сигнала и не учитывают контекст текущего прогноза. Фильтр может либо недостаточно подавить шум, либо, наоборот, исказить информативную структуру сигнала, сгладив важные детали. Во-вторых, цифровая фильтрация имеет фазовые искажения, особенно при применении рекурсивных IIR-фильтров, и требует либо двунаправленного фильтрования (что невозможно в режиме реального времени), либо дополнительных техник компенсации задержки. В-третьих, постобработка предсказания фиксированным фильтром разрушает согласованность между входом и выходом модели и препятствует реализации сквозного обучения с помощью градиентного спуска.

С практической точки зрения это означает следующее. Если фильтрация применяется уже после формирования прогноза нейросети, она становится внешним неподконтрольным компонентом, не включённым в процедуру обучения. Таким образом, градиенты ошибки не проходят через фильтр, и модель не может учитывать его поведение в процессе оптимизации. Это резко снижает точность, адаптивность и интерпретируемость всей системы в целом. Только встроенные обучаемые сглаживающие слои, являющиеся дифференцируемыми и включёнными в вычислительный граф модели [5], позволяют корректно решать задачу стабилизации выхода без потери чувствительности к физиологическим переходам.

В нейросетевых решениях для прогнозирования временных рядов фильтрация выходных сигналов может реализовываться разными способами. Один из подходов – применение фильтров с конечной импульсной характеристикой (FIR) [6], когда сигнальная последовательность x ( t ) свёртывается с обучаемым ядром порядка N :

y ( t ) = Z N = 0 h m x ⁽ t - m ) ’ ⁽¹⁾ где x ( t ) – входная последовательность (тензор выходов RNN); y ( t ) – отфильтрованный выход; h _m – обучаемые коэффициенты ядра порядка N .

Другим методом является слой экспоненциального скользящего среднего (EMA), задающийся рекурсивным уравнением y (t) = ax(t) + (1 -a)y (t -1), (2) где a G (0,1] - параметр сглаживания; y (t - 1) - предыдущий выход фильтра, что обеспечивает постепенное затухание высокочастотных флуктуаций без разрыва градиента и сохраняет простоту реализации внутри LSTM-блока [7].

Не менее распространённым решением выступает слой скользящего среднего (Moving Average Layer), который усредняет каждую новую точку по M предыдущим:

^{y (} t ) = MM I M - x [ t - m ^] ’ ⁽³⁾ где M – ширина окна усреднения; несмотря на детерминированность, такой слой часто применяется для первичной стабилизации прогноза, например, в задачах моделирования работы тоннелепроходческих машин [8].

Адаптивный спектрально-инерционный слой на основе обучаемой маски фурье-преобразования для фильтрации выходных данных...

Другим подходом является слой на основе дискретного косинусного преобразования (DCT-слой), где сигнал сначала преобразуется дискретным косинусным преобразованием t - 1           ( n p ( 2 n + 1 ) ^

X ⁽ P ) = E n = 0 x ⁽ t ) ■ cos [ _2T j ’                        (4)

где T – длина блока преобразования; p – индекс косинусного коэффициента (частотный канал);

Далее его спектр умножается на обучаемую маску m _p, а восстановление во временную область происходит через обратное DCT:

1 ^t - 1              ( n p ( 2 n + 1 ) ^

y ⁽ t ) = t E p = 0 m P X ⁽ p ) ■ cosy    _{2 T}   j ■                   (5)

Подобная структура DCT позволяет точечно управлять каждой частотой и адаптироваться к спектральным особенностям данных [9]. Следует подчеркнуть, что рассматриваемый DCT-слой не является процедурой зауживания концов сегмента временного ряда при вычислении дискретного преобразования Фурье (далее – ДПФ). Дискретное косинусное преобразование представляет собой самостоятельное преобразование в частотной области и не требует оконной предобработки. В данном случае параметр p обозначает индекс косинусного коэффициента (частотного канала), а не параметр оконной функции.

Более гибким, но всё ещё ограниченным подходом является использование слоя на основе быстрого преобразования Фурье (далее – БПФ), реализуемого как отдельный этап пост-обработки предсказаний рекуррентной сети [10; 11]. В таких моделях выходной сигнал нейросети преобразуется в частотную область, после чего все компоненты выше заданной частоты среза f _c обнуляются.

Формально такой подход может быть выражен следующим образом. Пусть y ( t ) – предсказанная последовательность, а ^ { y ( t ) } = X ( f ) - её спектр. Тогда спектральная фильтрация задаётся через пороговую маску m _h( f ), определяемую как

[1, f < f mh(fHo r                           (6)

L 0, ^f >  ^fc

Итоговый сглаженный сигнал получается после ОБПФ:

y ( t ) = ^ ^{- 1} { X ( f ) m h ( f ) } .                             (7)

Это позволяет эффективно подавлять высокочастотные шумы, но лишает модель возможности адаптивно изменять форму фильтра и гибко подстраиваться под специфику конкретных данных. Важно также отметить, что такие фильтры обычно реализуются как фиксированные блоки постобработки, не участвующие в процедуре обучения, что ограничивает потенциал оптимизации всей модели.

Ни один из рассмотренных подходов не учитывает необходимость сохранения физиологически обоснованного спектрального состава выходного сигнала. В связи с этим предлагается адаптивный спектральный слой, основанный на преобразовании Фурье с обучаемой маской амплитуд, позволяющий сглаживать предсказания в частотной области в процессе обучения нейросети. Для компенсации краткосрочных скачков и моделирования инерционных свойств физиологических процессов предложенный слой дополняется экспоненциальным фильтром первого порядка, действующим во временной области. В совокупности эти два механизма – спектральная фильтрация и инерционная стабилизация – реализуют подход, позволяющий получить гладкий и физически правдо-

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

подобный выходной сигнал. После формирования основного прогноза LSTM-моделью выходная последовательность преобразуется в спектральную область с помощью быстрого преобразования Фурье, корректируется по частотам с использованием обучаемой маски, а затем обратным преобразованием Фурье (ОБПФ, iFFT) возвращается в временную область. Такой подход обеспечивает подавление высокочастотного шума без искажения физиологически значимых колебаний. Формально операция спектральной фильтрации выглядит как

X (f ) = Г {y (t)},

X (f ) = X (f) m (f), y (t ) = Г-1 {X (f)}, где y(t) – исходная выходная последовательность RNN, X(f) – её спектр; m(f) – обучаемая спектральная маска; y (t) - сглаженный сигнал, подаваемый в качестве окончательного прогноза.

Обучаемая маска m ( f ) инициализируется таким образом, чтобы на частотах, превышающих заранее заданную пороговую f _c, устанавливалась небольшая величина, что обеспечивает мягкое подавление высокочастотных шумов без грубых обрезок. Для f ≤ f _c маска принимает значения, близкие к единице. В процессе обучения нейросети значения элементов m ( f ) корректируются совместно с остальными параметрами модели, позволяя адаптивно подбирать границы фильтрации и степень сглаживания в зависимости от особенностей тренировочного набора.

Поскольку именно начальное значение f _c определяет исходную форму маски и влияет на характер подавления шумов, этот параметр становится ключевым для всей процедуры спектральной фильтрации. Неверный выбор частоты среза может привести либо к недостаточной фильтрации артефактов, либо, наоборот, подавлению значимой информации, отражающей физиологическую динамику.

С целью обоснованного выбора значения f _c предлагается использовать метод Уэлча (Welch’s method), являющийся стандартным подходом для оценки спектральной плотности мощности (Power Spectral Density – PSD) физиологических временных рядов [12]. Метод позволяет выявить диапазон частот, в котором сосредоточена основная энергия сигнала, и тем самым определить допустимый порог отсечения.

Оценка спектральной плотности мощности по методу Уэлча задаётся как

? ( “ к ) = K s K - 0 P x m ( » к ) •                     <»>

^W где SX (гоk) - усреднённая PSD на частоте wk; K - число перекрывающихся сегментов;

P_x ( го _k ) - периодограмма m -го сегмента.

Периодограмма для каждого сегмента определяется как рх. (гок) = MSM-w(t)■x(t + m*R)■e-j-”-■ k'N2,           (12)

где x ( t+mR ) – отсчёты m -го сегмента длины M ; ω( t ) – оконная функция длины M (окно Ханна); M – длина сегмента; R – шаг между сегментами (определяет степень перекрытия); N – длина БПФ; k – индекс частотного бина.

Адаптивный спектрально-инерционный слой на основе обучаемой маски фурье-преобразования для фильтрации выходных данных...

По полученному оценочному спектру (11) верхняя граничная частота выбирается как первая частота, на которой уровень PSD опускается ниже заранее заданного порога, обычно равная 10 %. То есть если определить пороговый уровень мощности как

Phresh = O^m^Sf (® k),(13)

то индекс частотного бина, соответствующий частоте среза, kcut = min ( k ), при условии

SW fak )< Pthresh , а частота среза fC =Юku .

Такой подход позволяет количественно и визуально определить характерные диапазоны частот, преобладающие в реальных физиологических данных, и использовать их для инициализации маски m ( f ) в спектральном фильтре. Таким образом, частота f _c, найденная по методу Уэлча, задаёт исходную форму обучаемой маски и служит опорной точкой для дальнейшей адаптации параметров в процессе обучения.

При этом метод Уэлча изначально предполагает разбиение исходного временного ряда на K перекрывающихся сегментов длины M с шагом R , вычисление периодограмм для каждого сегмента по формуле (12) и их последующее усреднение в соответствии с формулой (11). Такая процедура обеспечивает интеграцию («сшивку») локальных спектральных оценок и устраняет случайные колебания, присущие отдельным сегментам. В настоящей работе частота среза f _c определяется именно по усреднённой спектральной плотности мощности (11), а не по локальным оценкам f _c( m ). Это гарантирует согласованность и устойчивость определения пороговой частоты и позволяет корректно инициализировать спектральную маску m ( f ) для дальнейшего обучения модели.

Следует отметить, что метод Уэлча с окном Ханна является базовым и общепринятым подходом. Однако в дальнейшем возможно применение более совершенных окон (например, Блэкмана – Харриса) и многооконных спектральных оценок (multitaper spectral analysis – MTSA), обладающих улучшенными частотными характеристиками. В данной работе ограничились методом Уэлча как наиболее распространённым и воспроизводимым способом.

В основе предлагаемого метода лежит идея организовать окончательную фильтрацию прогноза в частотной области, опираясь на свойства БПФ и ОБПФ.

Пусть на выходе рекуррентной модели формируется одномерная временная последовательность y ( t ), где t = 0, 1, …, T -1 – дискретные моменты времени, а T – длина окна, выбранная для прогнозирования физиологического временного ряда. Предполагается, что y ( t ) уже представляет собой окончательный выход сети, который, однако, содержит нежелательные высокочастотные колебания. Задача состоит в том, чтобы адаптивно подавить эти помехи, сохранив при этом всю полезную информацию низкочастотного диапазона, характерного для биологической динамики.

Для этого первым шагом выполняется прямое дискретное преобразование Фурье (далее – ДПФ) сигнала y ( t ). Под ДПФ в данной постановке понимается переход от временного ряда к его спектру, который можно записать в виде

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

X ( ^k ) 11 = 11 S ". у ( t ) ^x ee

- j x 2 xnx k x t

T

k = 0,1,..., N_f - 1,

T где j = V-1, Nf =— +1 - количество бинов (частотных отсчётов) в спектре БПФ для вещественного входа. Здесь X(k) – комплексный спектр сигнала, соответствующий частоте fk и = н kfs,

где f _s – частота дискретизации, Гц, исходного временного ряда.

Таким образом, k = 0 описывает постоянную (нулевую) составляющую, а k = Nf– 1 со- ответствует частоте, максимально приближённой к s (частоте Найквиста). Это позволяет перейти к частотной области и количественно охарактеризовать вклад различных гармонических компонент в структуру прогноза.

Следующий шаг заключается в том, чтобы ввести обучаемый вектор весов

{ m k } N о — ¹,

который количественно определяет коэффициент прохождения для каждой частоты f _k. Инициализация элементов этого вектора выполняется так, чтобы при f _k≤ f _c, где f _c – заранее заданная пороговая частота, значения были близки к 1, а при f _k >  f _c имели бы небольшую величину α. Формула инициализации записывается как

( о ),, I 1, f k ^ f c mV ^ц = 1             .                               (21)

К f k >  ^fc

Частота среза fc выбирается с учётом физиологических ограничений. Например, диа- пазон низких частот, описывающих ритмику дыхания, лежит в пределах нескольких десятых герца; частоты выше 0,2…0,3 Гц в большинстве случаев считаются шумом, так как человеческий организм не производит колебаний быстрее этого диапазона.

После построения начальной маски m_k производится поэлементное умножение комплексного спектра X ( k ) на соответствующий вес m _k. Это даёт новый спектр

J X ( k ) Ц = Ц X ( k ) m k .                               (22)

Поскольку X ( к ) имеют размерность, а m k е ^ , произведение X ( к ) на m k остаётся комплексной величиной, однако сохраняется симметрия спектра БПФ – нижняя половина бинов (0 до N _f- 1) задаёт всю информацию о вещественной последовательности. Именно благодаря этому можно восстанавливать сигнал ОБПФ.

Обратное преобразование записывается обновлённой формулой

( j x 2 xnx k x t ^

у ( t ) н = H T S 2 о ^{- 1} X ( k ) x e ^1J,                       (23)

t = 0,1, . , T - 1.                                  (24)

Важно подчеркнуть, что итоговая последовательность у ( t ) является вещественной, так как комплексная часть исчезает за счёт совпадения положительной и отрицательной частотных составляющих.

Адаптивный спектрально-инерционный слой на основе обучаемой маски фурье-преобразования для фильтрации выходных данных...

Таким образом, прогнозируемая последовательность сначала преобразуется из временной области в частотную с помощью ДПФ. Полученный спектр корректируется путём поэлементного умножения на обучаемую маску, которая подавляет нежелательные частоты и сохраняет значимые компоненты сигнала. После этого выполняется ОПФ, в результате которого формируется сглаженный временной ряд с физиологически обоснованной структурой.

Вектор { m _k} выполняет функцию связи между временной и частотной областью. С одной стороны, он позволяет подавлять артефакты и высокочастотный шум, появившийся в итоговом прогнозе RNN, а с другой – сохранять физиологически значимую структуру низкочастотных колебаний. При обучении сети эти коэффициенты корректируются совместно с весами всех слоёв таким образом, чтобы получаемый сглаженный прогноз y ( t ) как можно точнее соответствовал эталонному физиологическому временному ряду y _true( t ).

Следующий компонент разработанного слоя – инерционный фильтр первого порядка, реализованный во временной области в виде разностного уравнения

У ои< ( t ) = ^ах y ( t ) + ( 1 -^а ) ^Х У out ( t — 1 ) ,                          ⁽²⁵⁾

0 < а <  1,                                   (26)

где у ( t ) - сглаженная последовательность, полученная после спектральной фильтрации, α – параметр сглаживания, определяющий степень влияния текущего и предыдущего значения. При α ≈ 1 фильтр практически не влияет на выход, при α → 0 он действует как сильно усредняющий низкочастотный фильтр. Фильтр не имеет собственной памяти или задержки во входном буфере, но обеспечивает экспоненциальное затухание краткосрочных флуктуаций. Благодаря своей рекурсивной форме он обеспечивает эффективное подавление остаточных колебаний в выходной последовательности модели, не искажая её низкочастотную структуру.

В текущей реализации параметр α является обучаемым скаляром, оптимизируемым в процессе обучения. Такой подход позволяет автоматически подобрать уровень сглаживания, но его значение остаётся постоянным для всех прогнозов. Перспективным направлением развития является введение адаптивного параметра сглаживания, значение которого может зависеть от характеристик сигнала или состояния модели. Это позволит более гибко учитывать изменения динамики физиологических временных рядов.

Представленное уравнение реализует стандартную схему экспоненциального скользящего среднего (Exponential Moving Average – EMA), широко используемую в анализе временных рядов. Такой подход обеспечивает эффективное подавление краткосрочных высокочастотных флуктуаций, сохраняя при этом долгосрочную динамику сигнала. Простота реализации и рекурсивная структура делают EMA удобным средством постобработки в задачах, где требуется снижение шумов в предсказанных временных рядах без значительного искажения общей формы сигнала.

Для оценки практической значимости разработанного слоя проведена серия экспериментов на задаче прогнозирования легочной вентиляции (далее – ЛВ) спасателей и промышленного персонала при прохождении маршрута с заданной физической нагрузкой с использованием изолирующего дыхательного аппарата.

Для обучения и тестирования использовался набор данных, включающий 16 маршрутов различной продолжительности (в среднем по 2000…3000 сек.) с посекундной за-

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

писью, синхронизированных с физиологическими параметрами. Данные были разделены на обучающую и валидационную выборки (15 маршрутов) и отдельный тестовый маршрут (1 маршрут) для проверки качества обобщения. При таком объёме данных модели демонстрировали устойчивую сходимость, что подтверждается кривыми обучения (см. Рисунок 3) и итоговыми метриками (см. Таблицу 2). Вопрос о минимально достаточном объёме обучающей выборки выходит за рамки данной работы и может рассматриваться в дальнейших исследованиях.

В качестве прогностической модели использовалась рекуррентная модель на базе LSTM, обучаемая по индивидуальным физиологическим и маршрутным данным. В тестировании использовались двухслойная LSTM, возвращающая прогноз временного ряда y ( t ) без дополнительных фильтраций, и та же архитектура, но с добавленным обучаемым спектральным фильтрующим слоем на выходе.

Обе модели обучались на одном и том же наборе данных, состоящем из синхронизированных физиологических измерений и профиля физической нагрузки, отражающего маршрут передвижения специалиста в условиях аварийной ситуации. Особое внимание уделялось обеспечению полной идентичности условий обучения для обеих архитектур, чтобы исключить влияние сторонних факторов и гарантировать корректность сравнения.

Перед началом обучения зафиксированы генераторы случайных чисел для всех используемых библиотек. Это обеспечивает строго воспроизводимые начальные веса, одинаковое поведение оптимизатора и совпадение порядка подачи данных. Таким образом, базовая модель и модель с фильтрующим слоем стартовали с абсолютно одинаковой инициализацией, проходили обучение в идентичных условиях, с одними и теми же входными последовательностями, эпохами, объёмом данных и параметрами оптимизации. Единственным различием между ними являлось добавление спектрального фильтрующего слоя в конце архитектуры второй модели.

На Рисунках 1, 2 представлены результаты прогнозирования ЛВ на интервале длительностью более 2000 сек. На первом графике видны нереалистичные скачки и резкие ступеньки при изменении нагрузки. Это связано с тем, что базовая LSTM-сеть склонна переоценивать отклик дыхательной системы на изменение условий, особенно при переходах между сегментами маршрута.

На втором графике, полученном с применением фильтрующего слоя, видно, что временной ряд становится плавным, отсутствуют артефакты, нехарактерные для физиологического сигнала, а ключевые особенности, такие как пики дыхания при физической нагрузке, сохраняются.

Ключевые метрики сравнения качества модели с применением и без применения разработанного фильтрующего слоя сведены в Таблицу 1.

Применение фильтрующего слоя позволяет сократить ошибку MSE более чем на половину при том же количестве эпох обучения и повысить корреляцию с реальными данными почти до 0,989, что демонстрирует высокую точность и надёжность модели при применении в условиях, критичных к ошибкам прогноза.

Дополнительным преимуществом разработанного слоя является его способность ускорять процесс обучения модели, способствуя более быстрому достижению оптимума и улучшая обобщающую способность. Для количественного подтверждения этого пре-

Адаптивный спектрально-инерционный слой на основе обучаемой маски фурье-преобразования для фильтрации выходных данных...

Таблица 1

Сравнение ключевых метрик качества модели с применением и без применения разработанного фильтрующего слоя

Метрика	Без фильтра	С разработанным фильтрующим слоем	Улучшение, %
MSE (среднеквадратическая ошибка)	4,58	2,045	55,3
MAE (средняя абсолютная ошибка)	1,575	1,177	25,3
Коэффициент корреляции Пирсона r	0,974	0,989	1,54
Коэффициент детерминации R 2	0,945	0,975	3,17

Источник: здесь и далее таблицы составлены авторами.

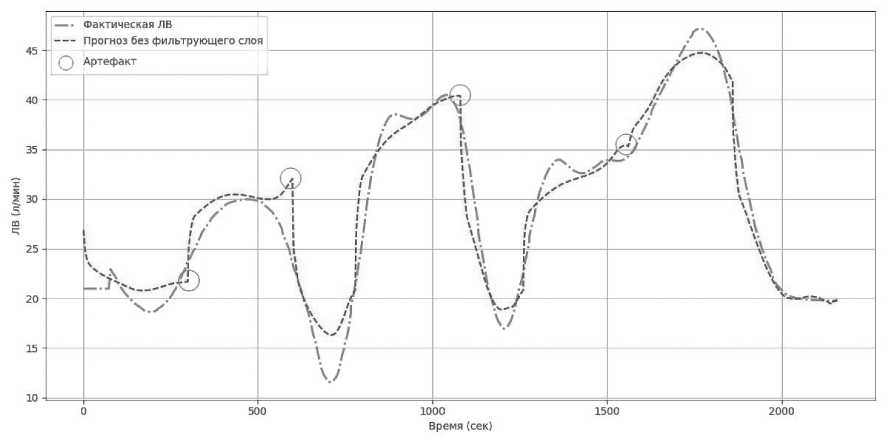
Рисунок 1. Прогноз лёгочной вентиляции без фильтрующего слоя Источник: здесь и далее рисунки выполнены авторами

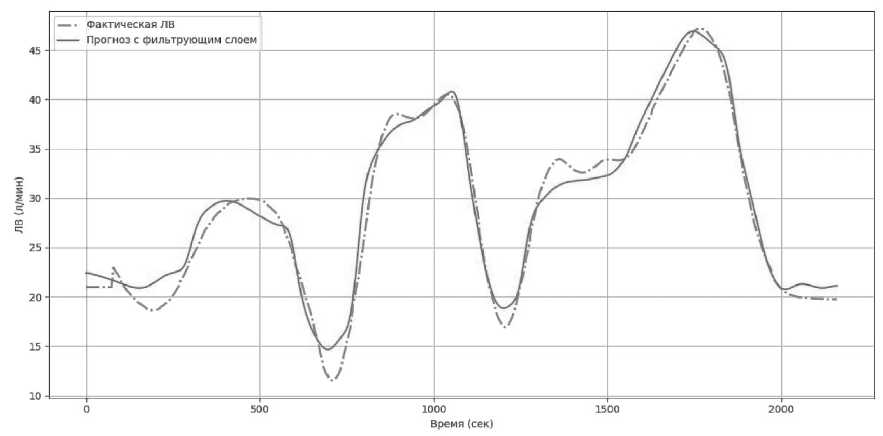
Рисунок 2. Прогноз лёгочной вентиляции с обучаемым спектральным фильтром

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

имущества был проведён эксперимент по сравнению обучения двух моделей – базовой LSTM (без фильтрации) и LSTM (с добавленным слоем спектральной фильтрации).

На Рисунке 3 представлены кривые сходимости по метрике MSE на валидационной выборке в течение 30 эпох.

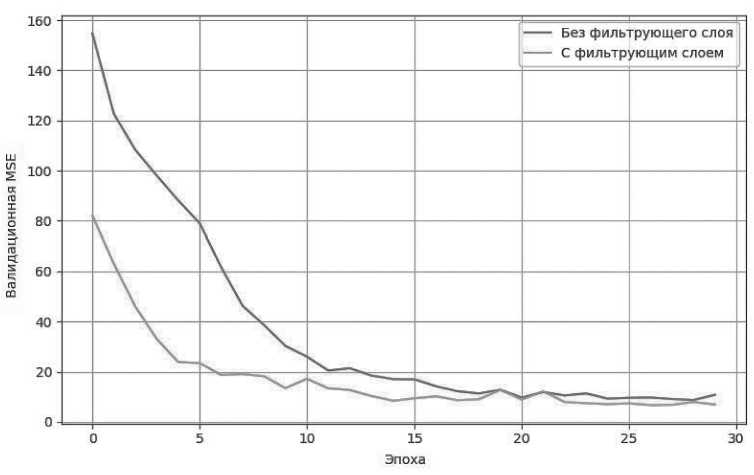
Рисунок 3. Динамика валидационной MSE по эпохам

Уже на начальных эпохах обучения модель с фильтрующим слоем демонстрирует существенное снижение ошибки, что указывает на быстрое приближение к релевантной структуре данных. К 5–6-й эпохе её ошибка снижается до уровня, который базовая модель достигает лишь к 12-му. В дальнейшем обе модели продолжают уменьшать ошибку. Таким образом, можно утверждать, что добавление разработанного слоя способствует ускоренной сходимости: модель быстрее обучается на значимых частотных компонентах и менее подвержена отвлечению на шум, присутствующий в целевой последовательности. Это делает процесс обучения не только более быстрым, но и более стабильным.

Для подтверждения эффективности разработанного слоя проведена серия тестов в идентичных условиях с использованием нескольких распространённых фильтрующих архитектур, рассмотренных ранее: фильтр с конечной импульсной характеристикой (FIR), экспоненциальное сглаживание (EMA), скользящее среднее, слой на основе дискретного косинусного преобразования (DCT), спектральный фильтр с фиксированной маской (FFT - LP), а также базовая модель без фильтрации. Все модели обучены на одном и том же наборе данных, а сравнение проведено в согласованных условиях, при которых параметры традиционных фильтров подобраны приближённо, в то время как в разработанном слое частота среза определена на основе анализа спектра методом Уэлча. Все сравниваемые фильтры применены как выходные слои нейросетевой модели, то есть воздействовали на предсказанную последовательность после основного блока RNN -прогнозирования. Это позволило провести корректное сопоставление по влиянию исключительно на форму выходного сигнала без влияния на архитектуру базовой сети [13].

Оценка проведена по следующим метрикам: E – эпоха, на которой достигается наи-

Адаптивный спектрально-инерционный слой на основе обучаемой маски фурье-преобразования для фильтрации выходных данных...

лучшее значение ошибки на валидации; E _50% – эпоха, на которой ошибка снижается до 50 % от начального значения; среднеквадратичная ошибка MSE и средняя абсолютная ошибка MAE на тестовой выборке; A _MSE– усреднённая MSE по всем эпохам; G _gap– разница между ошибкой на обучении и валидации (метрика обобщения); t _ep– среднее время одной эпохи обучения; TV ( Total Variation ) – показатель резкости предсказаний между соседними точками; SC ( Spectral Centroid ) – спектральный центр производной предсказания (характерная частота); R ² – коэффициент детерминации (доля объяснённой дисперсии).

Визуальные результаты сравнения разработанного слоя с существующими решениями представлены на Рисунках 4–8. На каждом из графиков отображено поведение метрики MSE на валидационном наборе данных в зависимости от номера эпохи. Уже с первых эпох видно, что модель с предложенным фильтром демонстрирует более быстрое и устойчивое снижение ошибки, в то время как альтернативные методы – фильтр с конечной импульсной характеристикой (FIR), скользящее среднее (Moving Average), дискретное косинусное преобразование (DCT), экспоненциальное сглаживание (EMA) и фиксированная спектральная маска (FFT-LP) – отстают как по скорости сходимости, так и по итоговому уровню ошибки.

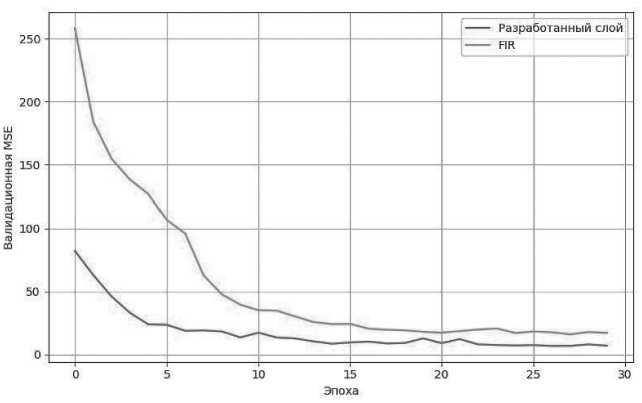
Рисунок 4. Сравнение разработанного слоя с FIR-фильтром

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

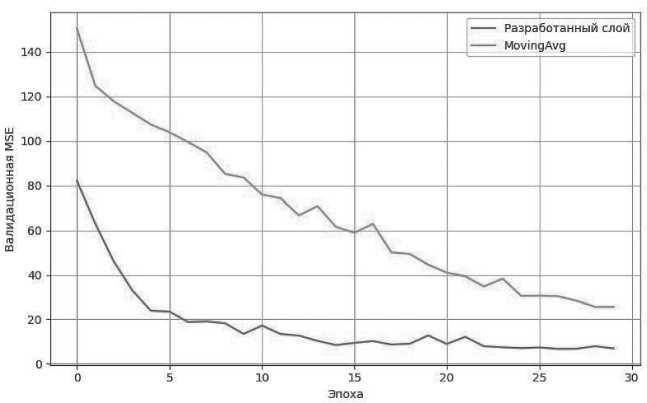
Рисунок 5. Сравнение разработанного слоя со скользящим средним

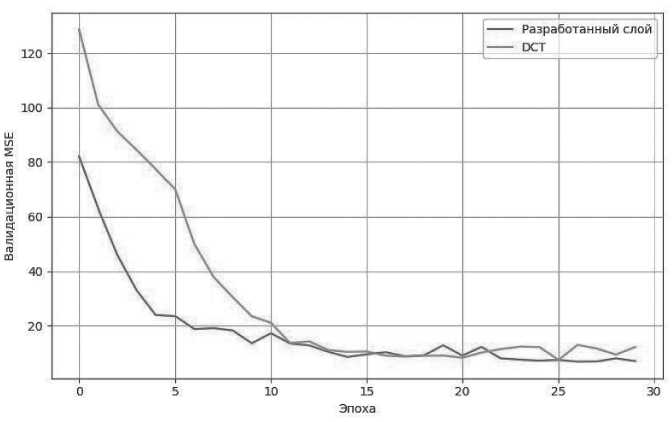
Рисунок 6. Сравнение разработанного слоя с DCT-фильтром

Таблица 2 содержит значения ключевых показателей качества, характеризующих точность, скорость сходимости, обобщающую способность и спектральную устойчивость выходных предсказаний. Сравнение включает как традиционные методы сглаживания, так и предложенный в данной работе спектрально-инерционный слой.

Разработанный спектрально-инерционный слой продемонстрировал наилучшие значения по абсолютным метрикам точности: минимальное значение средней квадратичной ошибки на тесте ( MSE = 7,35), минимальная средняя абсолютная ошибка ( MAE = 2,11) и максимальное значение коэффициента детерминации ( R 2 = 0,93), что свидетельству-

Адаптивный спектрально-инерционный слой на основе обучаемой маски фурье-преобразования для фильтрации выходных данных...

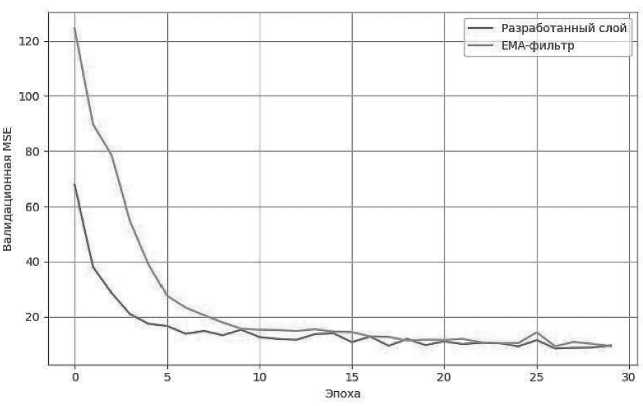
Рисунок 7. Сравнение разработанного слоя с экспоненциальным фильтром (EMA)

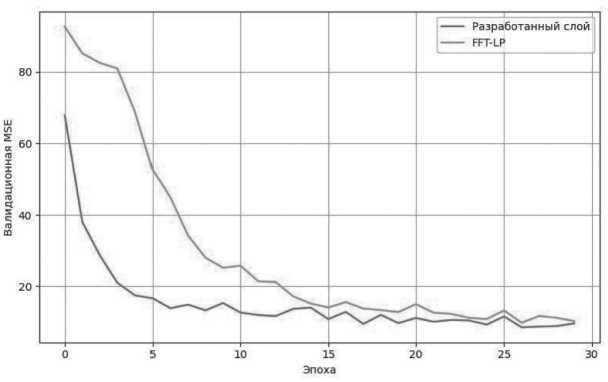
Рисунок 8. Сравнение разработанного слоя с фиксированной спектральной маской (FFT-LP)

Таблица 2

Сравнение выходных фильтрующих слоёв по метрикам точности и стабильности предсказания

Модель	E	E 50%	A MSE	G	t ep , с	MSE	MAE	TV	SC	R 2
Без фильтрующего слоя	28	6	36,66	-17,02	0,77	11,74	2,74	0,80	1265,53	0,88
Разработанный слой	26	3	17,76	-7,64	0,83	7,35	2,11	0,57	1308,5	0,93
FIR	27	4	54,85	-12,10	0,74	16,56	3,08	2,00	1289,5	0,83
EMA	26	4	24,62	–11,42	0,81	9,52	2,36	0,71	1298,9	0,89

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

Продолжение таблицы 2

Модель Ebest E 50% A MSE G tep, с MSE MAE TV SC R2 Скользящего среднего 29 11 67,27 -18,71 0,75 27,63 3,69 2,05 1106,1 0,72 DCT 25 6 30,60 -12,65 0,80 11,74 2,55 0,67 1302,8 0,88 FFT-LP 25 6 29,42 -11,62 0,79 10,79 2,53 0,99 1219,9 0,86 ет о высокой согласованности предсказаний с реальными физиологическими временными рядами. Кроме того, данный слой обеспечил наиболее низкие значения Total Variation (TV = 0,57) и наивысшее положение спектрального центра производной (SC = 1308,5), что говорит о сохранении адекватной физиологической формы сигнала без переусреднения.

Характерной особенностью разработанного слоя является ускоренная сходимость. Значение ошибки снижается до 50 % от начального уровня уже к 3-й эпохе ( E _50% = 3), тогда как альтернативные архитектуры требуют в среднем в 2–3 раза больше эпох. При этом значение G _gap = –7,64 указывает на низкую переобучаемость, что особенно важно в задачах с ограниченным объёмом данных.

Сравниваемые альтернативные решения демонстрируют существенно более слабые результаты. Так, FIR-фильтр, несмотря на обучаемость весов, показал значительное отставание по всем метрикам, как по MSE (16,56), так и по TV (2,00), что говорит о недостаточной способности подавлять шум без искажения сигнала. Более того, коэффициент детерминации у FIR остаётся на уровне 0,83, что ощутимо ниже предложенного варианта. Фильтр скользящего среднего, являясь неадаптивным и жёстко определённым, продемонстрировал наиболее высокую ошибку на тесте ( MSE = 27,63) и высокие значения TV (2,05), указывающие на нестабильность предсказаний. При этом R 2 = 0,72 является наименьшим среди всех участников сравнения, что подтверждает его ограниченность в условиях сложной динамики. Слой, основанный на дискретном косинусном преобразовании (DCT), показал умеренные результаты ( MSE = 11,74, R 2 = 0,88). Несмотря на способность к частотной фильтрации, жёсткая структура DCT-маски не обеспечивает достаточной гибкости для адаптации к особенностям сигнала, что выражается в относительно высоком значении TV (0,67). Слой EMA (экспоненциальное скользящее среднее) оказался одним из наиболее конкурентоспособных по ряду метрик (например, MSE = 9,52, R 2 = 0,89), но уступает разработанному слою по скорости сходимости, устойчивости и способности адаптироваться к изменениям частотной структуры. Это объясняется фиксированным характером фильтра и отсутствием спектральной селективности. Наконец, слой FFT-LP, реализующий отсекание частот выше фиксированной пороговой частоты, показал сравнимую с EMA точность ( MSE = 10,79), но значительно более высокую резкость предсказаний ( TV = 0,99), что указывает на наличие остаточных артефактов. Его коэффициент R 2 = 0,86 также ниже, чем у предложенного решения, а скорость сходимости хуже ( E _50% = 6).

Таким образом, предложенный спектрально-инерционный фильтрующий слой обеспечивает лучшую адаптивность, стабильность и физическую достоверность выходных предсказаний по сравнению с существующими подходами. Его использование позволяет не только повысить точность модели, но и улучшить интерпретируемость выходных прогнозов в задачах прогнозирования физиологических временных рядов.

Адаптивный спектрально-инерционный слой на основе обучаемой маски фурье-преобразования для фильтрации выходных данных...