ADPCM Image Compression Techniques for Remote Sensing Applications

Published Online May 2015 in MECS

Due to recent advancement in sensor technology, ISRO’s future remote sensing systems will have better spatial, radiometric, and spectral resolution. This improvement leads to higher data volume. Image compression is usually employed to meet transmission capability in space missions [1]. Compression ratio is usually decided by trade-off studies between available satellite resources and image quality requirement from user community.

DPCM, a prediction based image data compression techniques, has been used in many missions. Table-1 provides usage summary for DPCM and its adaptive part ADPCM [1].

Table 1. Usage of DPCM technique onboard

Satellite	Compressio n Algorithm	Compression Ratio		Implem entation
SPOT-I/II/III/IV (CNES1986/90/93/9 8)	Fixed Rate DPCM	8:6	1.33	-
Resourcesat-II (ISRO 2011)		10:7	1.41	FPGA
LANDSAT-7 (M7)	ADPCM Kodak	8:1.5	2.5,5	-
IKONOS     (US GeoEye1999)		11:2.5	4.4	ASIC Kodak
QuickBird     (US DigitalGlobe 2001)		11:X	-
WorldView-1  (US DigitalGlobe2007)		11:4	2.75, 4.3	ASIC Kodak
Chang’E-1 (China2007)	Differential Predictive (DPCM)	-	2	FPGA

In Resourcesat-2 (ISRO-2011) LISS-4 payload, DPCM technique was used with compression ratio of 10:7 [2]. This availability of 10-bit radiometric data leads to better image quality as compared to Resourcesat-1 (7-bit digitization) [3, 4]. Fig. 1 shows few onboard images (False Color image after fusion of multi-spectral data).

Fig. 2 shows typical histogram of an LISS-4 image (12000X12000). Kindly observe the non-linear axis.

Fig. 1. Resourcesat-2 LISS-4 images

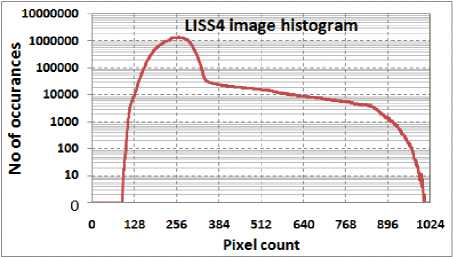
Fig. 2. Histogram of LISS-4 data

Implemented DPCM technique has quantizer dynamic range of 270 pixel difference counts, which was derived based on analysis of various payload images. But, difference count up to 600 was observed due to higher system MTF performance, which indicates that ringing artifacts are expected at high contrast locations [3]. Higher dynamic range of quantizer may force radiometric degradation at lower contrast locations. Existing technique also causes error propagation in recovery of 25% pixels [3].

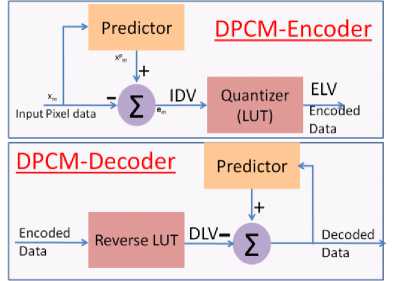
Fig. 3. Existing DPCM block diagram

II. Exisiting DPCM Technique in LISS-4 Payload

Block diagram of existing DPCM encoder/decoder [24] is shown in Fig. 3. DPCM is implemented in a group of pixels. In a single group, at least one pixel is transmitted in its original form (lossless). For remaining pixels, residue with predictor is quantized and transmitted [5].

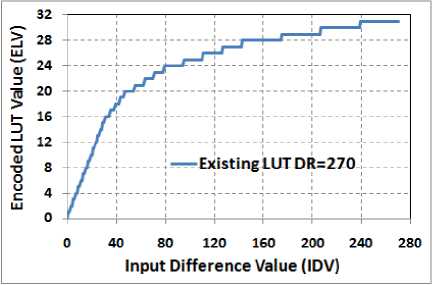
Fig. 4. Existing DPCM’s Quantizer (LUT)

Table 2: Algorithm of Existing DPCM Technique

DPCM operation for Odd Pixel Group
Input odd port data	P1 (10-bit)	P3 (10-bit)	P5 (10-bit)	P7 (10-bit)
DPCM Operation	P1 – P3	Ref Pixel	P3 – P5	P5 – P7
Output bits after LUT mapping & adding sign bit	6-bit	Original (Lossless) 10-bit	6-bit	6-bit
DPCM operation for Even Pixel Group
Input even port data	P2 (10-bit)	P4 (10-bit)	P6 (10-bit)	P8 (10-bit)
DPCM Operation	P2 – P4	P4– P6	Ref Pixel	P6 – P8
Output bits after LUT mapping & adding sign bit	6-bit	6-bit	Original (Lossles s) 10-bit	6-bit

Input Difference Value (IDV) i.e. the DPCM residue P1-P3 or similar is quantized through LUT and 6-bit (including one sign bit) Encoded LUT value (ELV) is generated. One of the pixels is sent without processing. Hence 25% data will be recovered losslessly.

Existing DPCM technique is developed with quantizer dynamic range of 270 IDV only, which was derived based on analysis of various payload images. But, IDV up to 600 count is possible due to higher system MTF performance, which indicates that ringing artifacts are expected at high contrast locations [3]. Dynamic range of existing LUT can be increased through bigger quantization step sizes, but this will degrade radiometric performance. Another issue with existing DPCM technique is error propagation i.e. error in recovery of P5 pixel affects P7 pixel’s recovery.

The issue of dynamic range coverage and radiometric performance can be resolved by multiple quantizers. Quantizers will be applied selectively as per input contrast per group. Quantizer with small step size will be applied at low contrast location; this will ensure better radiometric performance considering higher probability of such instances (60-90%). Quantizer with bigger step size will be applied at high contrast location. This will cover input dynamic range and reduce ringing artifacts. Requirement of multiple quantizers leads to Adaptive DPCM (ADPCM) technique, which is discussed in next section.

• III.    Development of ADPCM Techniques for LISS-4 Payload data configuration

Because of lower complexity, ADPCM with adaptive quantizer is considered for development [5]. In single ADPCM group, one pixel is transmitted in original form (lossless) [5]. For remaining pixels, residue i.e. difference with predictor is quantized by look up table (LUT). Fig. 5 shows block diagram of ADPCM technique.

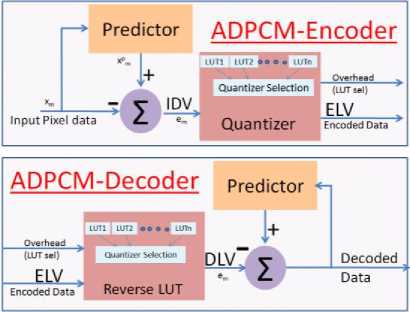
Fig. 5. ADPCM block diagram

• A.    Development of ADPCM-4P technique

ADPCM-4P technique requires compression of 4-pixel 40-bit data to 28-bit. One reference pixel will occupy full 10-bits. Three input difference values (IDV) i.e. DPCM residue are quantized through selected LUT. This generates three 6-bit (including sign bit) encoded LUT values (ELV). Hence, no spare bit is available to indicate used LUT in ADPCM. Requirement of 3 sign bit transmission can be omitted if all IDVs are positive. This is possible by selecting the pixel with smallest value as a predictor for remaining three pixels. But, predictor location information has to be transmitted along the encoded data which will require additional 2-bits. The remaining 1-bit can be used for LUT selection. Encoding of proposed ADPCM-4P technique for an odd pixel group is shown in Table 3 with all four combinations.

Table 3. Encoding of Proposed ADPCM-4P

REF Pixel	ODD Pixels	P1 (10-bit	P3 (10-bit)	P5 (10-bit)	P7 (10-bit	REF index	SEL LUT
P1	й .о 2 55 Он о 3 и Q	P1 (10-bit)	P3-REF (5-bit)	P5-REF (5-bit)	P7-REF (5-bit)	00 (2-bit)	СО '^
P3		P1-REF (5-bit)	P3 (10-bit)	P5-REF (5-bit)	P7-REF (5-bit)	01 (2-bit)
P5		P1-REF (5-bit)	P3-REF (5-bit)	P5 (10-bit)	P7-REF (5-bit)	10 (2-bit)
P7		P1-REF (5-bit)	P3-REF (5-bit)	P5-REF (5-bit)	P7 (10-bit)	11 (2-bit)

For low contrast group, lossless LUT (LUT-DR-31) is applied. This means IDV values are transmitted without any losses. For high contrast group, lossy piecewise linear LUT (LUT-DR-600) is applied. LUT-DR-600 will cover full input dynamic range and helps in avoiding ringing artifacts. Fig. 6 shows details of both these LUTs. Proposed LUTs commensurate with expected IDV histogram, shown in Fig. 7. Kindly observe non-linear axis in plot.

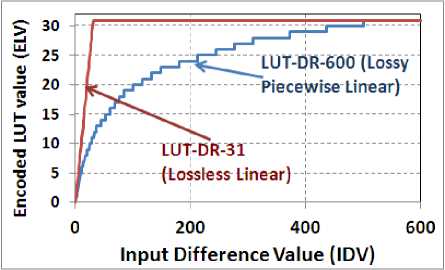
Fig. 6. Proposed ADPCM’s Quantizer Details

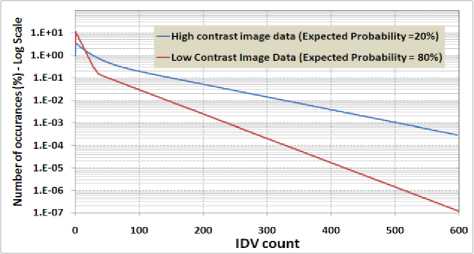
Fig. 7. Histogram of expected IDV counts

m — 1 n — 1

RMSE =    - ZZ I ref ( (, j )   ¹ re cov ered (i, j)]²

m.n ( = 0 j = o

where [m n] is image size. I REF is considered reference image-set for simulation purpose, while I recovered is decompressed image.

Entropy ( bits / pixel ) = log 2

Z ( . p ( ( )

. ( = 0

p ( ( ) = probabiliyof ( th count

One of the main advantages of this technique is zero error propagation. However, this leads to poor prediction because reference pixel can be one of the four pixels. If it is P1 or P7, then poor correlation may increase residues and then quantization errors. Requirement of pixel sorting slightly increases hardware implementation complexity.

• B.    Development of ADPCM-5P technique

Algorithm of proposed ADPCM-5P technique for an odd pixel group is shown in Table 4. A group of 5 adjacent pixels is processed at a time. Details of required quantizers are already mentioned in Fig. 6.

Table 4. Algorithm of Proposed ADPCM-5P

Odd Pixels	P1 (10-bit)	P3 (10-bit)	P5 (10-bit)	P7 (10-bit)	P9 (10-bit)	SEL LUT
DPCM Operation	P1-P3 (6-bit)	P3-P5 (6-bit)	REF= P5 (10-bit)	P5-P7 (6-bit)	P7-P9 (6-bit)	S (1-bit)

∆E P3 = DLV (ELV(IDV P1-P3 )) – IDV P1-P3 (1)

∆E P7 = DLV (ELV(IDV P7-P9 )) – IDV P7-P9 (2)

Rather than quantizing P1-P3 & P7-P9 data, P1-P3+∆E P3 & P7-P9-∆E P7 will be quantized respectively. This technique is termed as ADPCM-5P-NEP (no error propagation).

• IV.    RMSE Simulation Results

Line Complexity =

|       m n — 1

-    ZZIIref (i, J + 1) — Iecovered (i, J)| m (n -1) i=0 J=0

Line complexity is computed from across track odd pixel data.

Fig. 8. Image-sets used for simulation

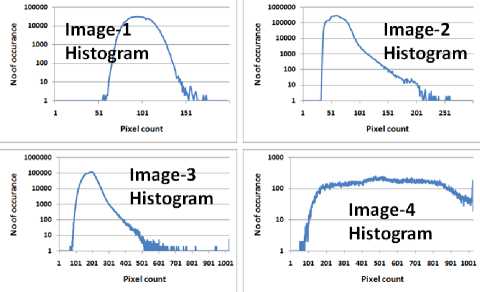
Fig. 9. Histogram of simulation image-sets

Table 5: Simulation Image-sets parameters

	Mean	Std.	Max D)V	IDA" Entropy	Complexity
Imagel (1000X1000)	97.4	11.9	71	3.4	8.1
Image! (3000X3000)	60.1	12.4	182	2.5	43
Image3 (3000X3000)	184.6	32.5	799	3.9	13
Imagel (360X360)	553.5	221.1	794	6.5	95.8

Fig. 13. Recovered data statistics with ADPCM-4P

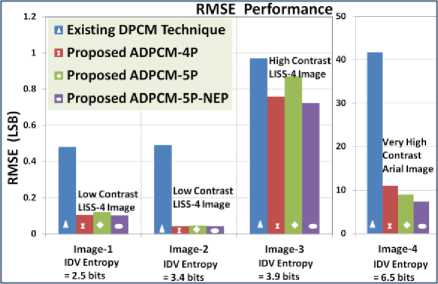
Fig. 10. RMSE performance comparison

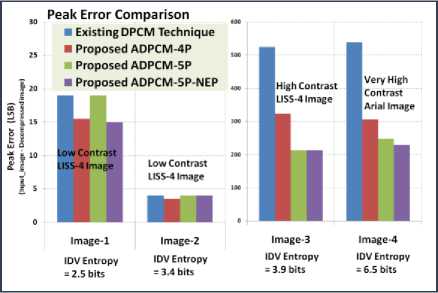
Fig. 11. Peak Error Performance Comparison

Lossless pixels ■ Lossy pixels

Image-1 Image-2 Image-3 Image-4

(Low          (Low         (High        (Very High

Contrast)Contrast)Contrast)Contrast)

Fig. 12. Recovered data statistics with ADPCM-5P

• V.    Ringing Artifacts Simulation Results

12 pixel one dimensional worst case simulation dataset is developed as per system MTF. In uniform regions, ringing artifacts are computed by using Equation 6. Fig. 14 shows simulation results. Proposed ADPCM technique reduce ringing artifacts to <1.5%.

RingingArtifacts ( RA %)

p   ( P n -1 + P n +1)

P n ^-2      *100

( P n -1  ⁺ P n +1)

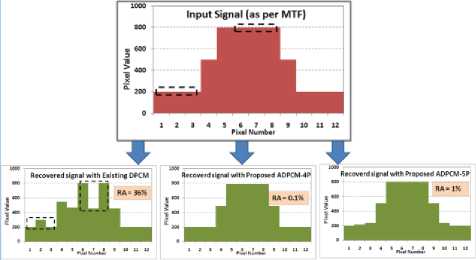
Fig. 14. Ringing artifact simulation with 12-pixel one dimensional data

Simulation dataset (8X8 pixel matrix) with maximum contrast is developed as per LISS-4 system MTF [3]. Fig. 15 shows simulation results (color mapped). In uniform along track and across track regions, ringing artifacts are computed by using Equation 6. Proposed ADPCM techniques reduce ringing artifacts to <1.5%.

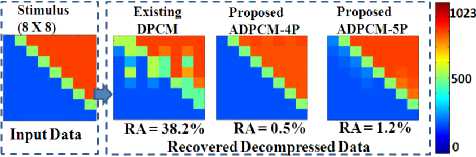
Fig. 15. Ringing Artifacts Simulation with 8X8 matrix (2-D dataset)

In recovered image 1 to 4 [Fig. 8], no visual ringing artifacts were observed. For visual analysis, some artificial high intensity objects were inserted in image-4. Recovered images are shown in Fig. 16. It can be concluded that ADPCM reduces ringing artifacts significantly.

Fig. 16. Ringing Artifacts simulation results on image-4

From above analysis, it can be noted that ringing artifacts cannot be eliminated fully, as these arise because of quantization. Artifact pattern and its extent depend on encoding technique and quantization table. Other space agencies have also reported DPCM noise in recovered image. Fig. 17 shows noise due to ADPCM compression, reported for IKONOS PAN images [7, 8].

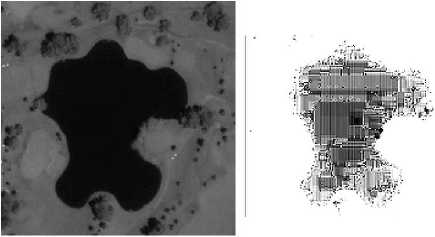
lake in Reid Park, Tucson

DM 200-220 contrast-stretched

Fig. 17. DPCM noise observed in IKONOS PAN Image

• VI.    Conclusion

The proposed novel ADPCM techniques shows better image reproducibility compared to existing DPCM technique. New ADPCM techniques maintain the compression ratio of 10:7 and achieve significant radiometric improvement on low as well as high contrast images compared to existing DPCM technique. Developed ADPCM techniques produce RMSE of 10 counts compared to 41 counts for very high contrast image. These produces RMSE of 0.04 counts compared to 0.48 counts with low contrast images. Ringing artifacts are reduced to 0.5% compared to 38.2%. Algorithm of both techniques has low complexity.

Acknowledgment

We gratefully acknowledge the constant encouragement and guidance received from Shri Arup Roy Chowdhury – GD-SEG, Shri R M Parmar-DD-SRA, Shri DRM Samudraiah- Prof. Satish Dhawan Scientist, Shri Saji A Kuriakose–DD-SEDA and Shri A. S. Kiran Kumar-Director SAC. We are thankful to our colleagues of Payload Checkout Electronics Group for providing the images.